Transformer模型详解
Transformer模型详解
参考自台大李宏毅老师课件
Transformer模型是谷歌大脑在2017年底发表的论文Attention Is All You Need[1]中所提出seq2seq模型。而Transformer这个seq2seq模型的特别之处是模型当中大量用到了Self-Attention这种特别的Layer。因此首先我们需要来了解的是Self-Attention这种特别的Layer。
1 Self-Attention
1.1 RNN
如果我们谈到处理一个Sequence,我们最常想到拿来用的network架构就是RNN(如下图),如果是如图的Bi-directional的RNN,当我们输出
b
1
b^1
b1~
b
4
b^4
b4时,我们已经把整个input Sequence通通都看过了,因此RNN经常用于处理input是一个序列的情况下,但RNN有一个问题:Hard to parallel!(不容易并行计算)。
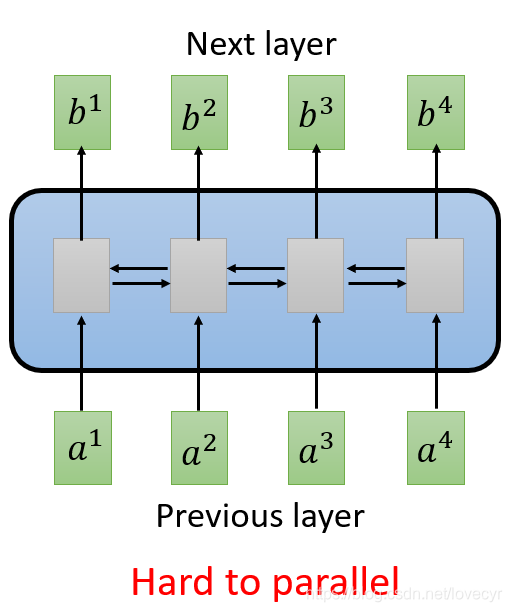
因此有人提出用CNN来代替RNN。当我有一堆filters的时候CNN也可以做到输入是一个sequence而输出也是一个sequence,同时CNN是可以并行计算的。但是,CNN这里的每个filter只考虑了非常有限的内容。当然我们叠多层filter,其实也能看到非常丰富的内容,不过对于第一层来说还是很难做到获取很长一个序列的资讯。
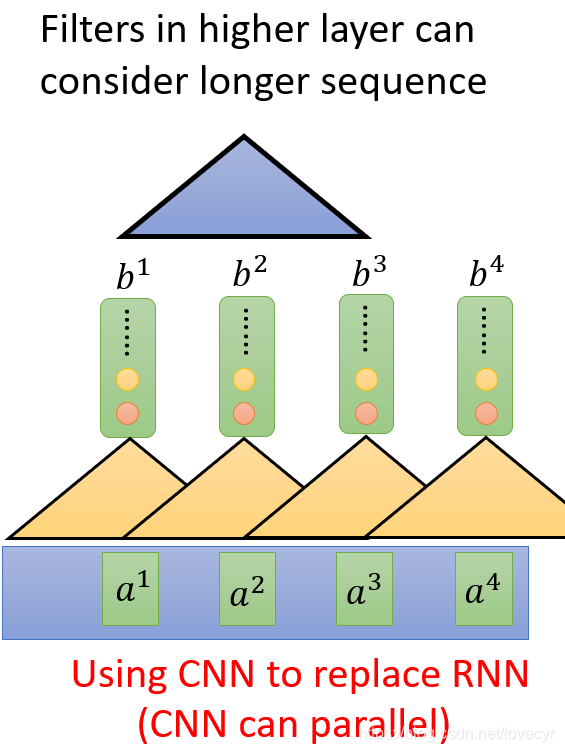
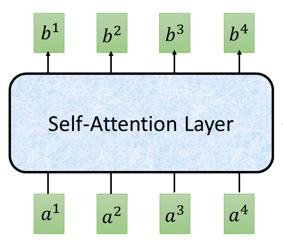
因此,这里就引出了我们所要讲到的内容——Self-Attention Layer
1.2 Self-Attention Layer
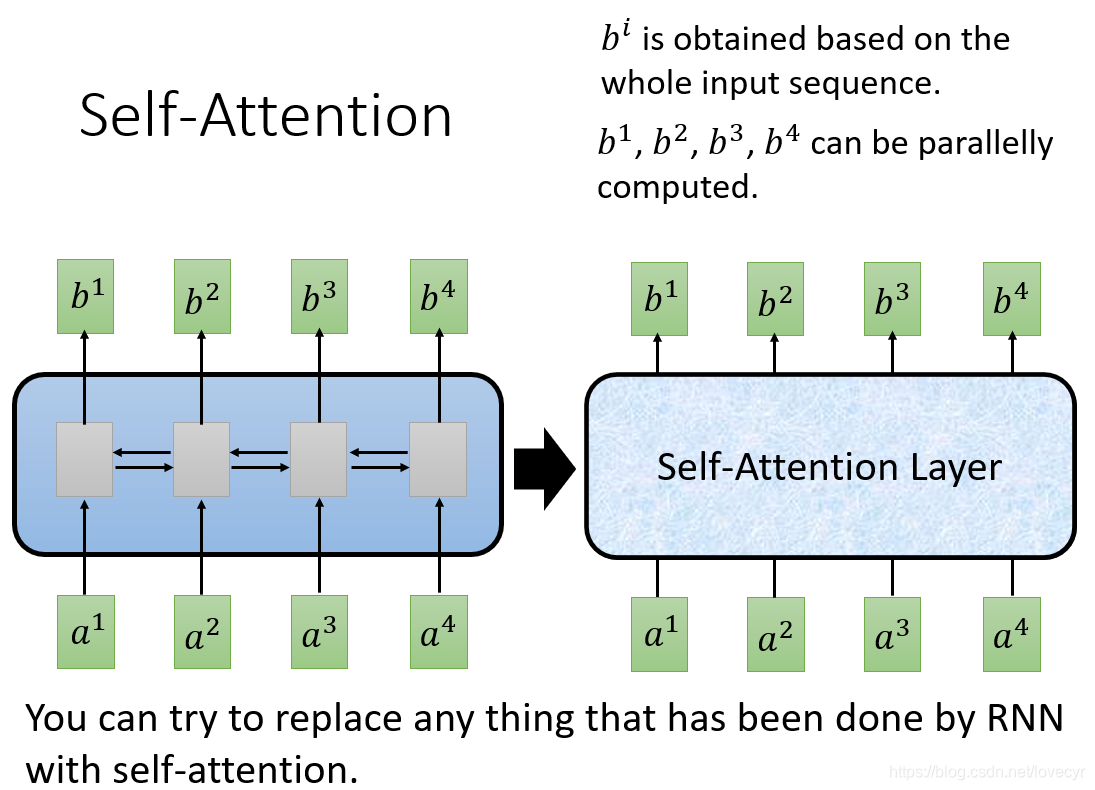
在这个Self-Attention layer中对于每个输出
b
i
b^i
bi都来自于整个input sequence,其次,对于整个输出
b
i
b^i
bi,是可以并行计算的。因此可以说的是基本上所有RNN能做的事用Self-Attention Layer都可以做。
1.3 Self-Attention怎么做的?
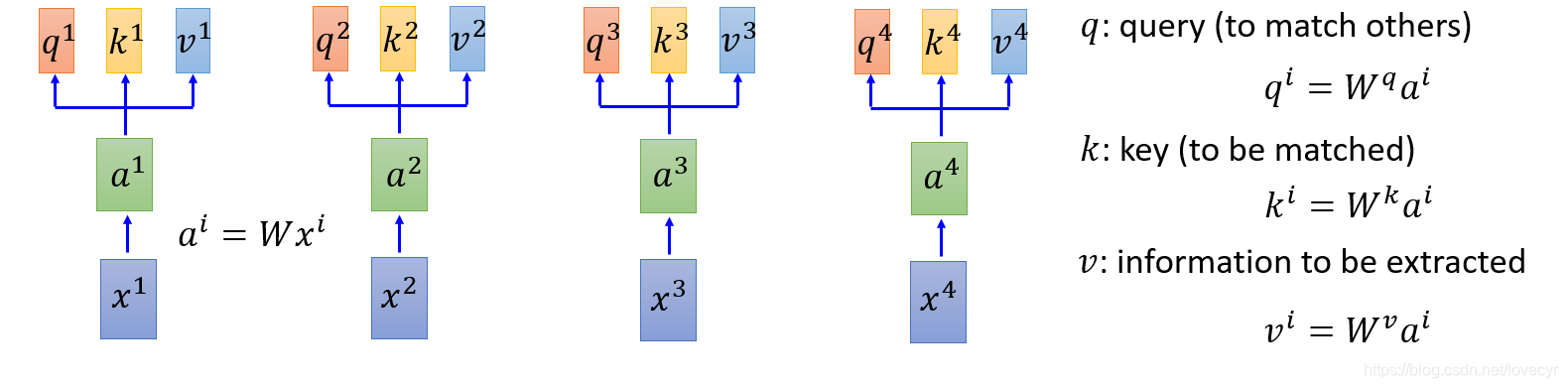
在Self-Attention Layer中,我们先用每个input
a
i
a^i
ai分别乘上3个不同的Matrix得到3个不同的Vector,这个3个Vector分别命名为q、k、v。其中每个Vector的作用如图所示。
接下来我们要做的是:拿每个query q对每个key k去做Attention(如下图所示)
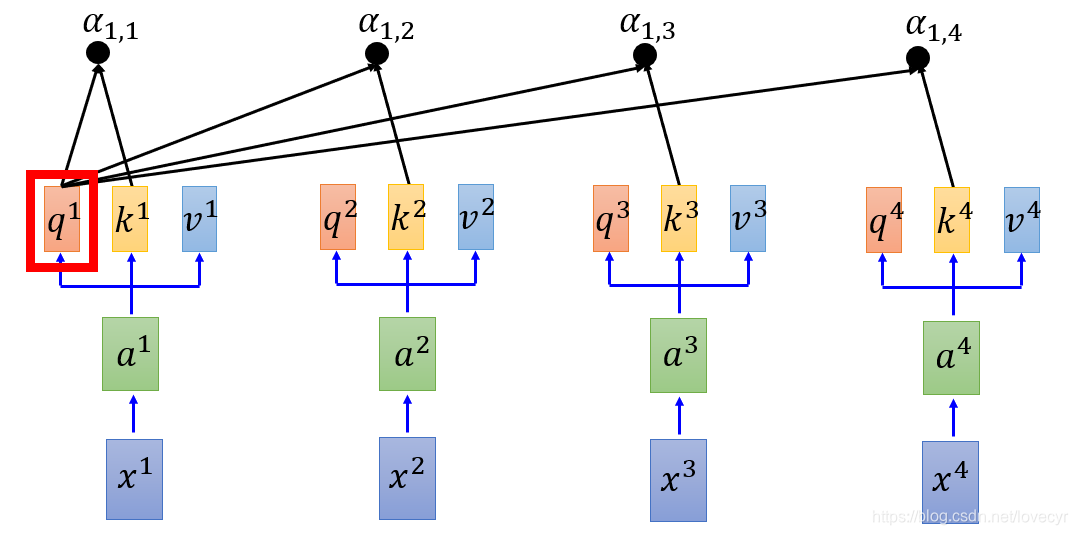
那么这个Attention做了一个什么事呢?这里我们直接给出attention的式子:
S
c
a
l
e
d
D
o
t
−
P
r
o
d
u
c
t
A
t
t
e
n
t
i
o
n
:
a
1
,
i
=
q
1
⋅
k
i
d
(
d
i
s
t
h
e
d
i
m
e
n
s
i
o
n
o
f
q
a
n
d
k
)
Scaled \ Dot-Product \ Attention:a_{1,i} = \frac{ q^1 \cdot k^i }{\sqrt{d}} (d\ is\ the\ dimension\ of\ q\ and\ k)
Scaled Dot−Product Attention:a1,i=dq1⋅ki(d is the dimension of q and k)
这里有一个问题,就是为什么除以 d \sqrt{d} d?
假设两个d维向量每个分量都是一个相互独立的服从标准正态分布的随机变量,那么他们的点乘结果会很大,并且服从均值为0,方差就是d(很大的点乘会让softmax函数处在梯度很小的区域),对每个分量除以 d \sqrt{d} d可以让点乘的方差为1。
再接下来我们做一个softmax:
a
^
1
,
i
=
exp
(
a
1
,
i
)
∑
exp
(
a
1
,
j
)
\hat{a}_{1,i} =\frac{\exp(a_{1,i})}{\sum\exp(a_{1,j})}
a^1,i=∑exp(a1,j)exp(a1,i)
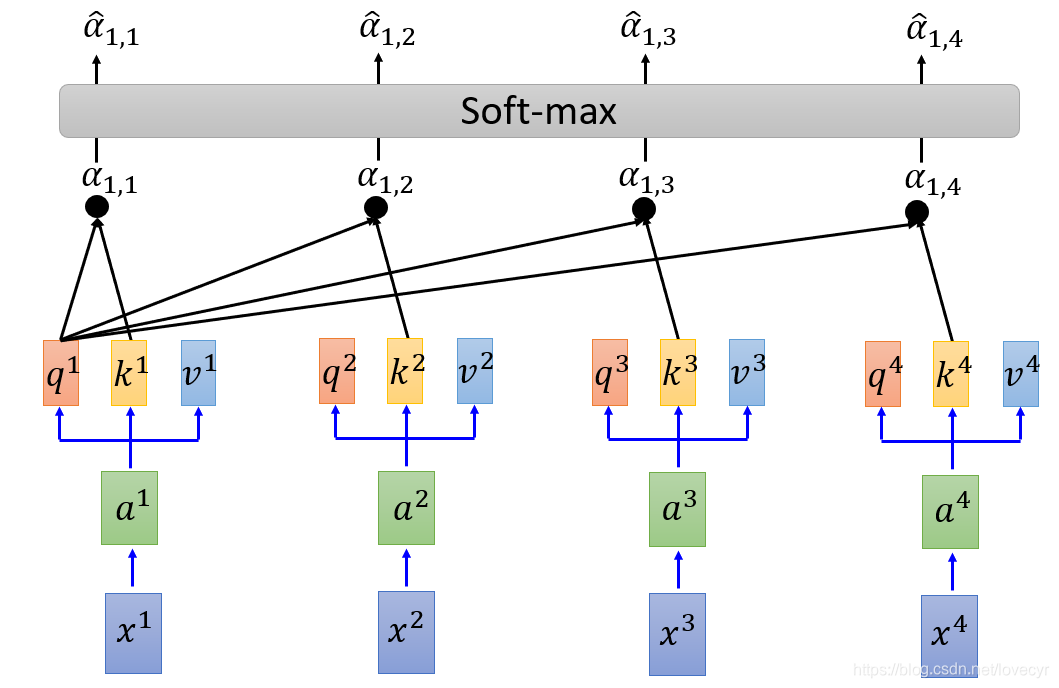
然后我们把得到的
a
^
\hat{a}
a^和v相乘再相加就可以得到我们的输出
b
i
b^i
bi:
b
1
=
∑
a
^
1
,
i
v
i
b^1 = \sum\hat{a}_{1,i}v^i
b1=∑a^1,ivi
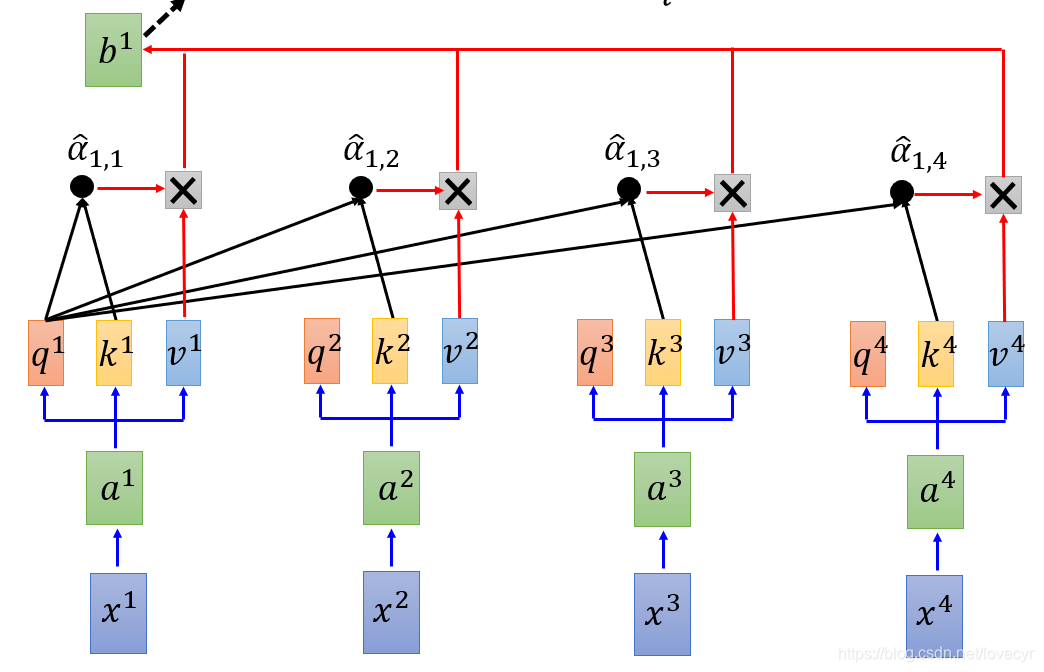 对于
b
1
b^1
b1来说,生成
b
1
b^1
b1已经考虑了整个sequence的资讯。
对于
b
1
b^1
b1来说,生成
b
1
b^1
b1已经考虑了整个sequence的资讯。
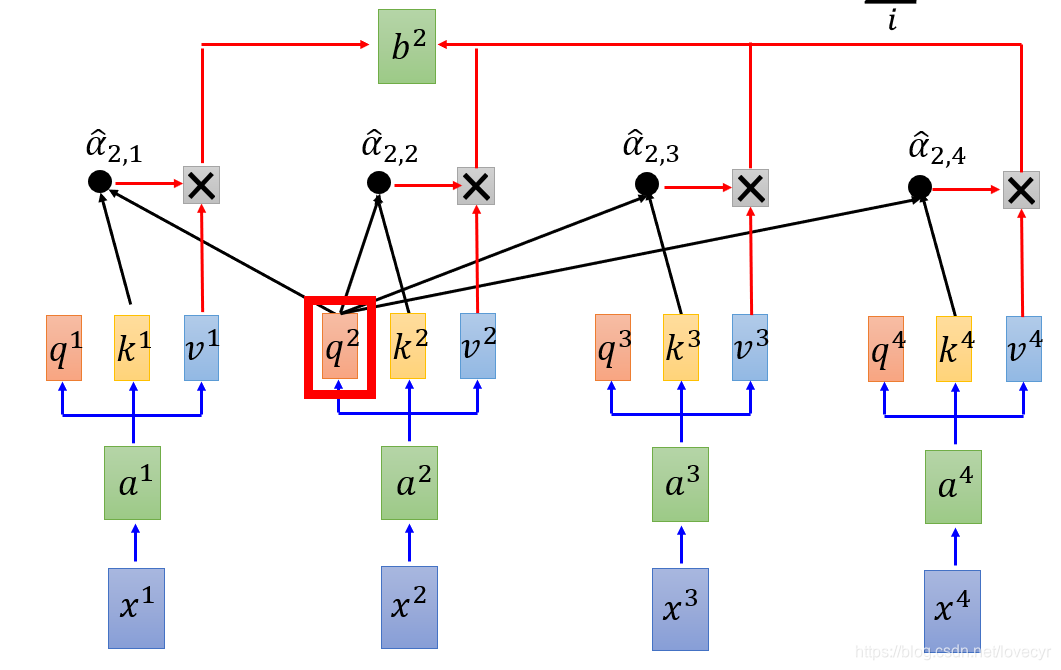
同理,在我们计算
b
1
b^1
b1的同时,也可以计算
b
2
、
b
3
、
b
4
b^2、b^3、b^4
b2、b3、b4:
b
2
=
∑
a
^
2
,
i
v
i
b
3
=
∑
a
^
3
,
i
v
i
b
4
=
∑
a
^
4
,
i
v
i
b^2 = \sum\hat{a}_{2,i}v^i \quad b^3 = \sum\hat{a}_{3,i}v^i \quad b^4 = \sum\hat{a}_{4,i}v^i
b2=∑a^2,ivib3=∑a^3,ivib4=∑a^4,ivi
1.4 Self-Attention运算的矩阵表示
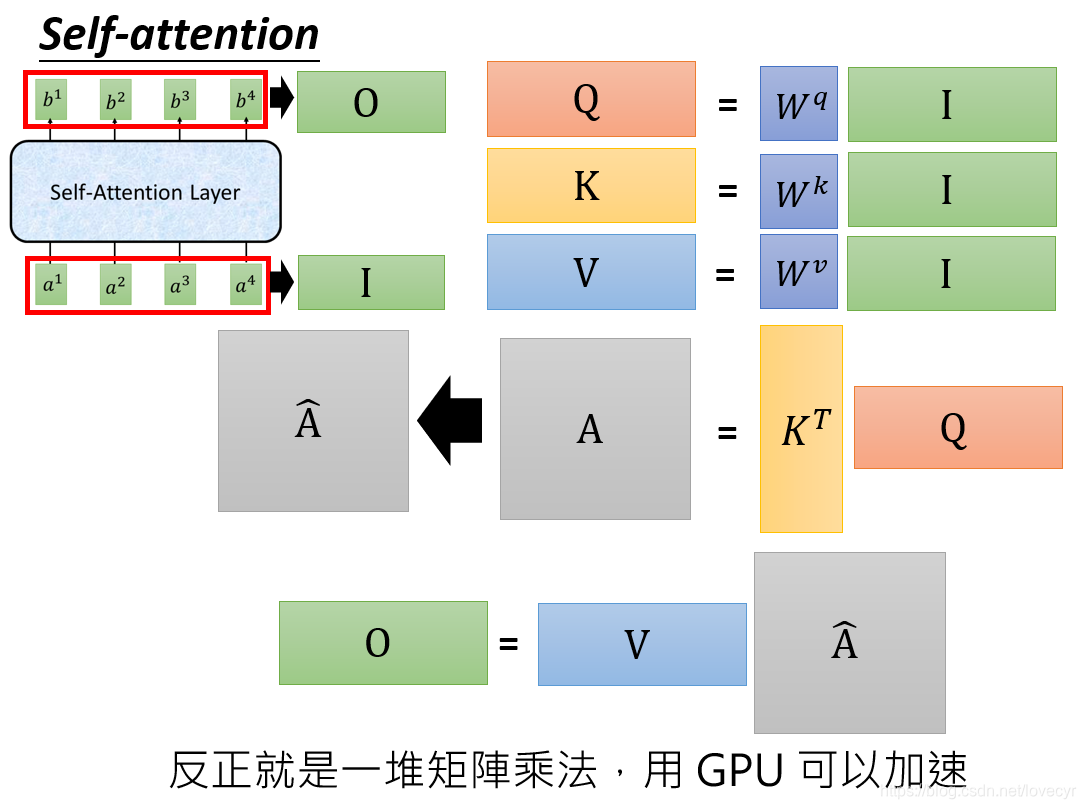
接下来我们来用矩阵运算来表示Self-Attention的运算过程,也可以以此顺明Self-Attention的运算过程为什么容易并行的。
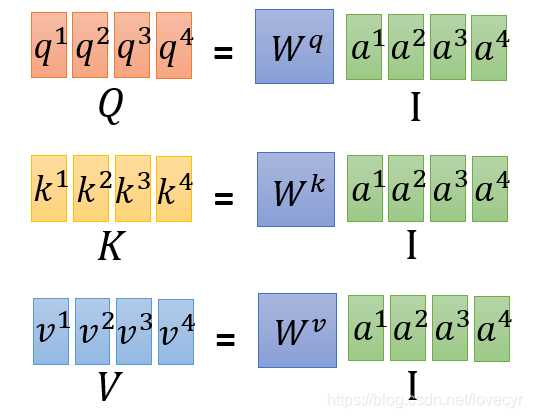
将每一个向量组成一个矩阵,对于矩阵Q,K,V,I中的一个column就代表一个向量,因此由
a
1
,
a
2
,
a
3
,
a
4
a^1,a^2,a^3,a^4
a1,a2,a3,a4得到Q,K,V是课并行的。
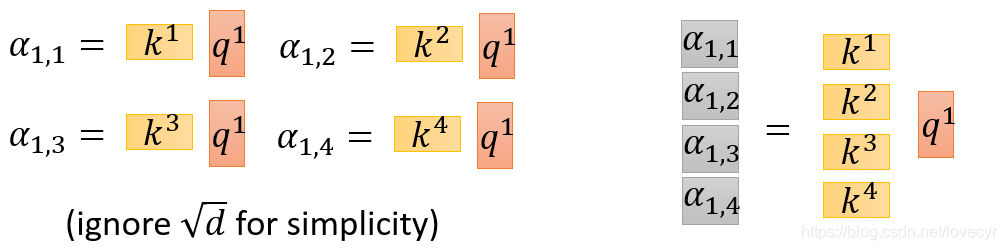
a
1
,
1
,
a
1
,
2
,
a
1
,
3
,
a
1
,
4
a_{1,1},a_{1,2},a_{1,3},a_{1,4}
a1,1,a1,2,a1,3,a1,4也可以通过上图所示的计算过程并行得出,接下来依然是一连串的矩阵运算:

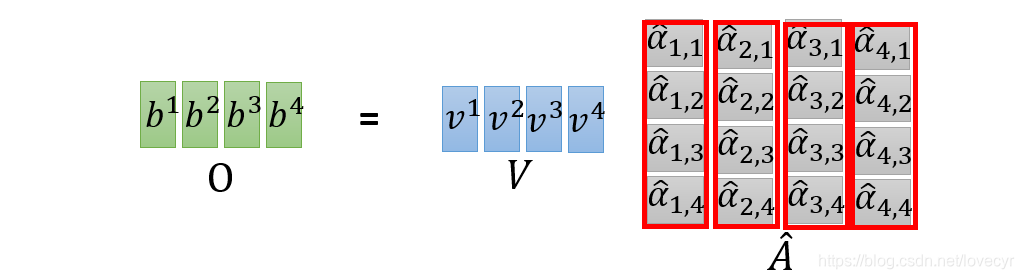
1.5 总结
2 变形:Multi-head Self-Attention (2 head as exam)
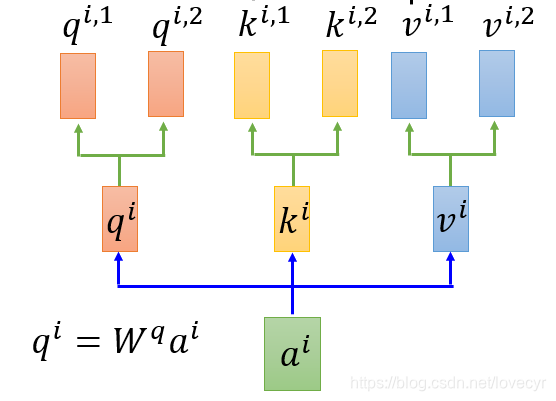
对于2 heads 的情况是:
q
i
q^i
qi分裂为2。
q
i
,
1
=
W
q
,
1
q
i
q
i
,
2
=
W
q
,
2
q
i
q^{i,1} = W^{q,1}q^i \quad q^{i,2} = W^{q,2}q^i
qi,1=Wq,1qiqi,2=Wq,2qi
2.1 Multi-head 情况下的Attention过程
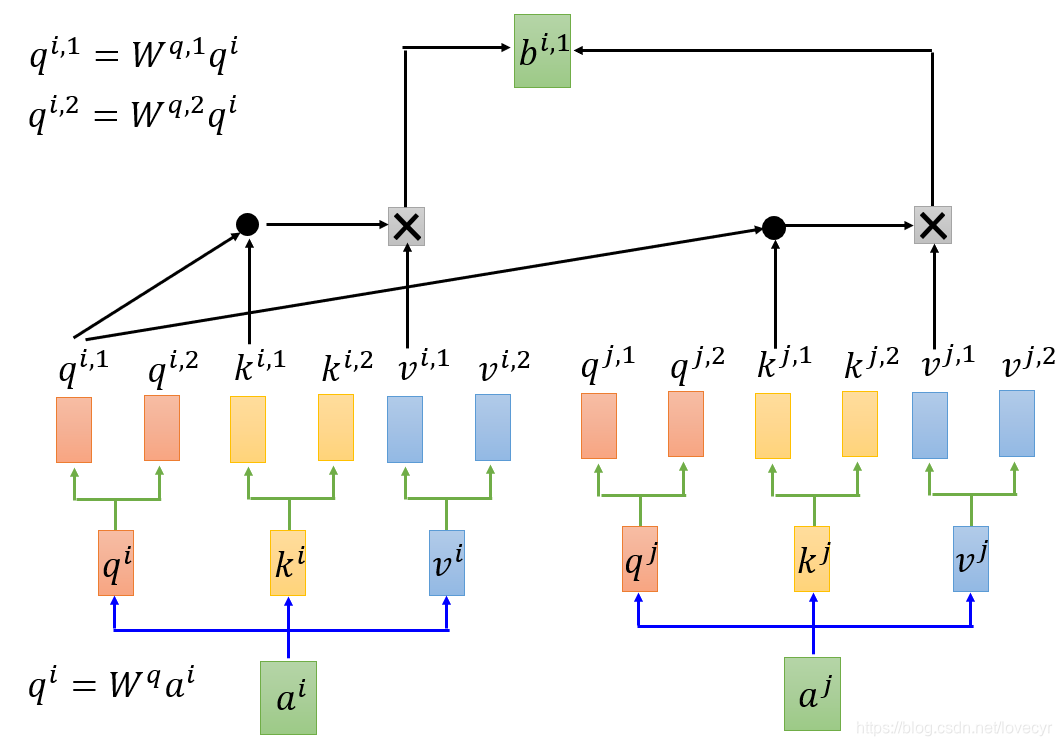
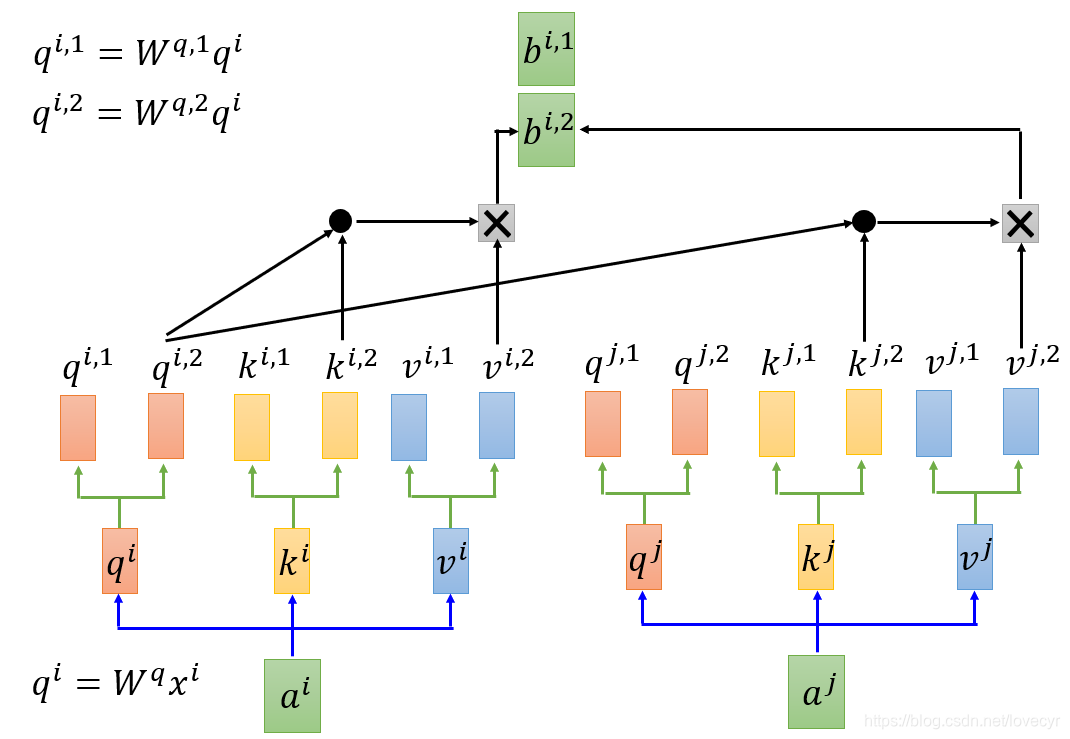
Attention过程如上图,
q
i
,
1
只
和
k
i
,
1
,
k
j
,
1
做
A
t
t
e
n
t
i
o
n
,
q
i
,
2
只
和
k
i
,
2
,
k
j
,
2
做
A
t
t
e
n
t
i
o
n
q^{i,1}只和k^{i,1},k^{j,1}做Attention,q^{i,2}只和k^{i,2},k^{j,2}做Attention
qi,1只和ki,1,kj,1做Attention,qi,2只和ki,2,kj,2做Attention,接下来我们直接将两个
b
i
b^i
bi接起来就可以作为我们的输出,当然如果你对这个输出的维度不满意的话,可以进行一定的降维处理(如下图)。
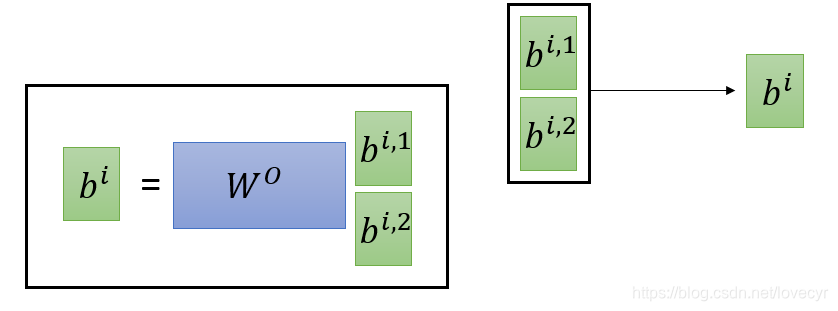
Multi-head的好处
那么,这个Multi-head方法有什么作用呢?通常我们不同的Multi-head关注的点是不一样的,举个例子来说,有的head关注的是相邻关系间的资讯,而有的关注的是一个较远距离之间关系的资讯,总的来说就是能使得我们的网络能够捕捉到更丰富的特征。
3 Positional Encoding
从上面的Self-Attention模型中你会发现:在该模型中并没有涉及到位置信息。
那么原论文是怎么做的呢?
Original paper: each position has a unique positional vector
e
i
e^i
ei(not learned from data),其实就是加上了一个手动设置的
e
i
e^i
ei。
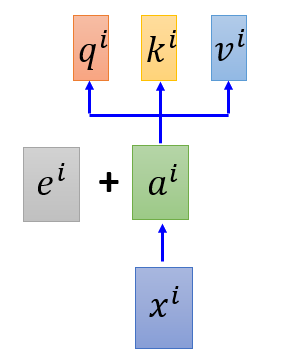
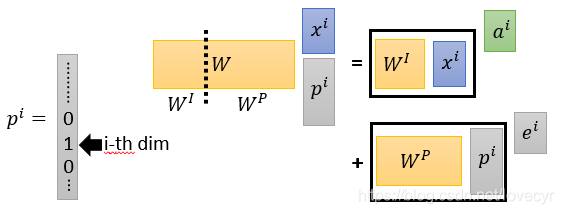
这里我们换一个说法:each
x
i
x^i
xi appends a one-hot vector
p
i
p^i
pi,也就是说我们在最原始的输入
x
i
x^i
xi阶段就加上一个ont-hot编码,然后再乘上一个Matrix W,而这个W我们可以将其拆成
W
I
W^I
WI和
W
P
W^P
WP来看待,当W和
x
i
x^i
xi,
p
i
p^i
pi做矩阵乘法后的结果就可以看作是
e
i
+
a
i
e^i+a^i
ei+ai。
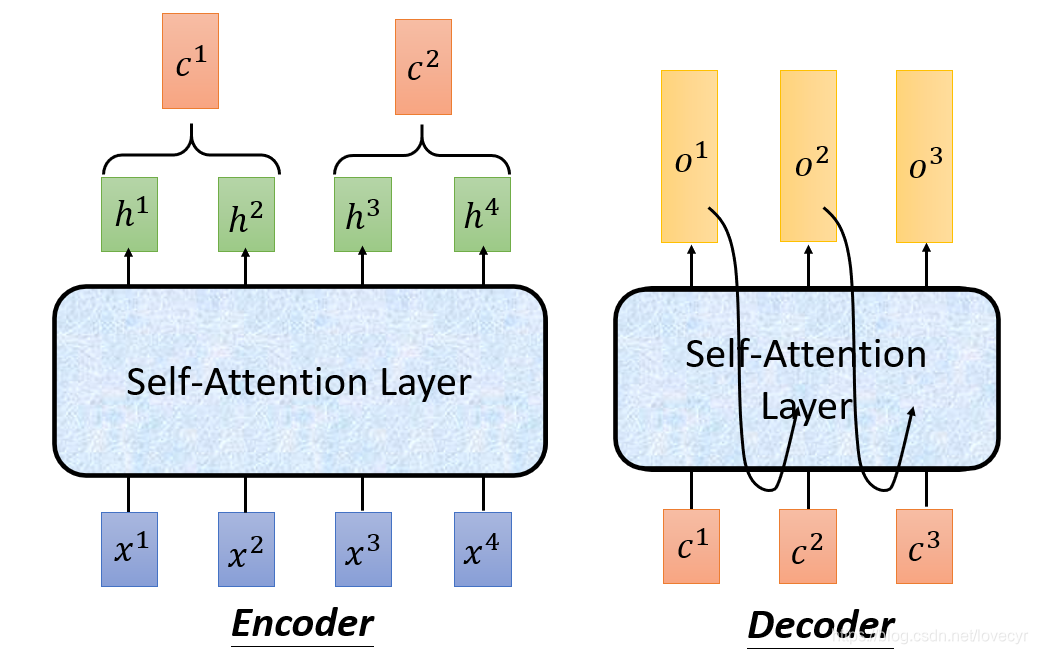
4 Seq2seq with Attention
Seq2seq: 2 个RNN组成;;Encode + Decoder
为了并行计算,可以用Self-Attention Layer来替换RNN(如下图)
5 Transformer
接下来我们来看一看我们的Transformer模型:
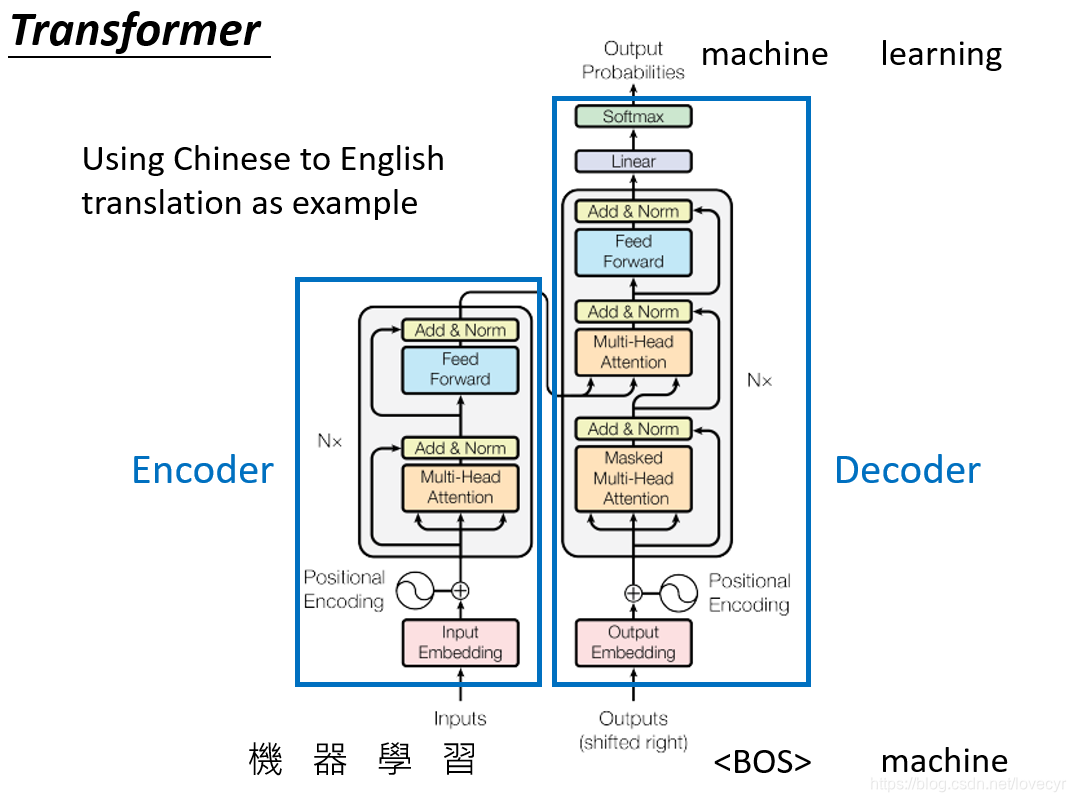
整个Transformer模型分为Encoder和Decoder部分。
首先我们先来看Encoder部分,从下往上看:
- Inputs通过Input Embedding layer转化为一个vector。
- 生成的vector加上一个Positional Encoding进入下一层。
- 接下来是个重复N次的灰色block,在这个block中
(1)首先是Multi-Head Attention层,输入一个sequence,输出是另一个sequence
(2)再接下来是Add&Norm层:其中Add是指吧Multi-Head Attention的output b和input a加起来得到 b ′ b' b′,这个Add的作用是为了防止梯度消失,将原输入加上经过网络层处理后的输出。
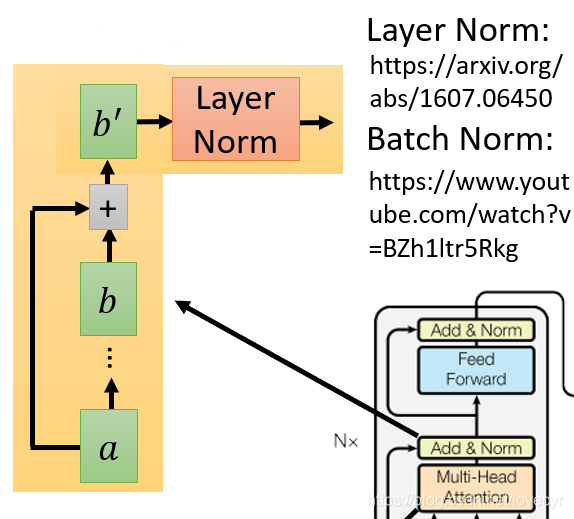
而Norm指的是Layer normalization,layer normalization相关论文在图中链接中。这里我们简单介绍一下:
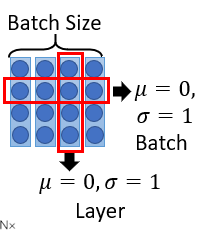
Batch Norm是指对同一个batch里面不同data的同样同样做归一化,我们希望整个batch里面的同一个维度的均值为0,方差为1.
而Layer Norm不需要考虑batch,给一笔data,我们希望它各个不同维度的均值为0,方差为1。
接下来是Decoder部分,对于Decoder部分只有几个地方与Encoder不同:
- 首先Decoder部分的Input是前一个time stamp所产生的output。
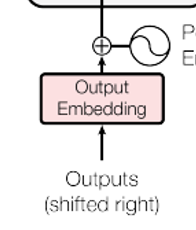
- 其中有一个Masked Multi-head Attention,这个Masked的意思是Attend on the generated sequence。通俗来说,解码过程是一个顺序操作的过程,也就是当解码第 k 个特征向量时,我们只能看到第 k-1 及其之前的解码结果,论文中把这种情况下的Multi-Head Attention叫做Masked Multi-Head Attention。
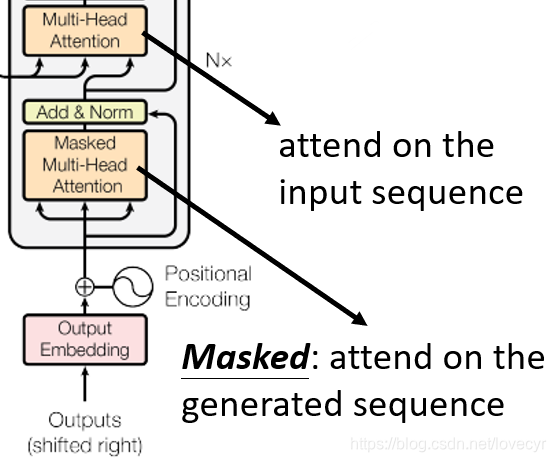
- 然后就是接下来有个Multi-Head Attention用到了之前Encoder部分的输出。
[1].Vaswani A , Shazeer N , Parmar N , et al. Attention Is All You Need[J]. arXiv, 2017.


 浙公网安备 33010602011771号
浙公网安备 33010602011771号