【Matlab开发】matlab中bar绘图设置与各种距离度量
【Matlab开发】matlab中bar绘图设置与各种距离度量
标签(空格分隔): 【Matlab开发】 【机器学习】
声明:引用请注明出处http://blog.csdn.net/lg1259156776/
Matlab Bar图如何为每个bar设置不同颜色
data = [3, 7, 5, 2;4, 3, 2, 9;6, 6, 1, 4];
b = bar(data);
使用bar绘制非常直观简单,但有时需要突出显示某一个bar,比如该bar是一个标杆,用来衡量其bar的高度,所以可以用醒目的红色来显示它。那么如何设置呢?
参看下面的代码:
data = [3, 7, 5, 2;4, 3, 2, 9;6, 6, 1, 4];
b = bar(data);
ch = get(b,'children');
set(ch{1},'FaceVertexCData',[1;1;1;1;2;2;2;2;3;3;3;3;4;4;4;4])
set(ch{2},'FaceVertexCData',[1;1;1;1;2;2;2;2;3;3;3;3;4;4;4;4])
set(ch{3},'FaceVertexCData',[1;1;1;1;2;2;2;2;3;3;3;3;4;4;4;4])
set(ch{4},'FaceVertexCData',[1;1;1;1;2;2;2;2;3;3;3;3;4;4;4;4])

data = [3, 7, 5, 2];
b = bar(data);
ch = get(b,'children');
set(ch,'FaceVertexCData',[0 0 1;0 1 1;1 1 1;1 0 1;])

matlab中用于求取各种距离的函数pdist方法的使用
引言说明
在机器学习和数据挖掘中,我们经常需要知道个体间差异的大小,进而评价个体的相似性和类别。最常见的是数据分析中的相关分析,数据挖掘中的分类和聚 类算法,如 K 最近邻(KNN)和 K 均值(K-Means)等等。根据数据特性的不同,可以采用不同的度量方法。一般而言,定义一个距离函数 d(x,y), 需要满足下面几个准则:
(1) d(x,x) = 0 // 到自己的距离为0
(2) d(x,y) >= 0 // 距离非负
(3) d(x,y) = d(y,x) // 对称性: 如果 A 到 B 距离是a,那么 B 到 A 的距离也应该是 a
(4) d(x,k)+ d(k,y) >= d(x,y) // 三角形法则:(两边之和大于第三边)
本节首先介绍一下matlab中用于求取各种距离的函数pdist方法的使用
matlab中用于求取各种距离的函数pdist方法的使用
下面是help出来的帮助信息:
help pdist
pdist Pairwise distance between observations.
D = pdist(X) returns a vector D containing the Euclidean distances
between each pair of observations in the M-by-N data matrix X. Rows of
X correspond to observations, columns correspond to variables. D is a
1-by-(M*(M-1)/2) row vector, corresponding to the M*(M-1)/2 pairs of
observations in X.
D = pdist(X, DISTANCE) computes D using DISTANCE. Choices are:
'euclidean' - Euclidean distance (default)
'seuclidean' - Standardized Euclidean distance. Each coordinate
difference between rows in X is scaled by dividing
by the corresponding element of the standard
deviation S=NANSTD(X). To specify another value for
S, use D=pdist(X,'seuclidean',S).
'cityblock' - City Block distance
'minkowski' - Minkowski distance. The default exponent is 2. To
specify a different exponent, use
D = pdist(X,'minkowski',P), where the exponent P is
a scalar positive value.
'chebychev' - Chebychev distance (maximum coordinate difference)
'mahalanobis' - Mahalanobis distance, using the sample covariance
of X as computed by NANCOV. To compute the distance
with a different covariance, use
D = pdist(X,'mahalanobis',C), where the matrix C
is symmetric and positive definite.
'cosine' - One minus the cosine of the included angle
between observations (treated as vectors)
'correlation' - One minus the sample linear correlation between
observations (treated as sequences of values).
'spearman' - One minus the sample Spearman's rank correlation
between observations (treated as sequences of values).
'hamming' - Hamming distance, percentage of coordinates
that differ
'jaccard' - One minus the Jaccard coefficient, the
percentage of nonzero coordinates that differ
function - A distance function specified using @, for
example @DISTFUN.
A distance function must be of the form
function D2 = DISTFUN(XI, XJ),
taking as arguments a 1-by-N vector XI containing a single row of X, an
M2-by-N matrix XJ containing multiple rows of X, and returning an
M2-by-1 vector of distances D2, whose Jth element is the distance
between the observations XI and XJ(J,:).
The output D is arranged in the order of ((2,1),(3,1),..., (M,1),
(3,2),...(M,2),.....(M,M-1)), i.e. the lower left triangle of the full
M-by-M distance matrix in column order. To get the distance between
the Ith and Jth observations (I < J), either use the formula
D((I-1)*(M-I/2)+J-I), or use the helper function Z = SQUAREFORM(D),
which returns an M-by-M square symmetric matrix, with the (I,J) entry
equal to distance between observation I and observation J.
Example:
% Compute the ordinary Euclidean distance
X = randn(100, 5); % some random points
D = pdist(X, 'euclidean'); % euclidean distance
% Compute the Euclidean distance with each coordinate difference
% scaled by the standard deviation
Dstd = pdist(X,'seuclidean');
% Use a function handle to compute a distance that weights each
% coordinate contribution differently
Wgts = [.1 .3 .3 .2 .1]; % coordinate weights
weuc = @(XI,XJ,W)(sqrt(bsxfun(@minus,XI,XJ).^2 * W'));
Dwgt = pdist(X, @(Xi,Xj) weuc(Xi,Xj,Wgts));
‘euclidean’,’seuclidean’,’cityblock’,’minkowski’,’chebychev’,’mahalanobis’,’mahalanobis’,’cosine’,’correlation’,’spearman’,’hamming’,’jaccard’分别对应着默认的欧式距离L2,标准欧式距离,城市距离(曼哈顿距离),闵可夫斯基距离,切比雪夫距离,马氏距离,夹角余弦,皮尔逊相关距离,斯皮尔曼等级相关距离(1-斯皮尔曼等级相关系数),汉明距离,杰卡德相似距离(1-Jaccard similarity coefficient)。还可以使用自定义的距离函数:Function,function D2 = DISTFUN(XI, XJ)。在有需要的时候再进行说明:
这里先对上面所讲到的那些距离进行简单的说明和总结,在下小节还会继续加强说明:
欧式距离L2
简单的说就是向量的L2范数,不必细讲,从小学似乎都知道了吧!
例子:计算向量(0,0)、(1,0)、(0,2)两两间的欧式距离:
X = [0 0 ; 1 0 ; 0 2]
D = pdist(X,'euclidean')
D =
1.0000 2.0000 2.2361
标准欧式距离
标准化欧氏距离是针对简单欧氏距离的缺点而作的一种改进方案。标准欧氏距离的思路:由于数据各维分量的分布不一样,先将各个分量都“标准化”到均值为0、方差为1。经过简单的推导就可以得到两个n维向量
标准化后的值 = ( 标准化前的值 - 分量的均值 ) /分量的标准差
注意这里的标准化,标准化的是分量之间,比如a,b的第一个分量
例子:计算向量(0,0)、(1,0)、(0,2)两两间的标准化欧氏距离 (假设两个分量的标准差分别为0.5和1)
X = [0 0 ; 1 0 ; 0 2]
D = pdist(X, 'seuclidean',[0.5,1])
D =
2.0000 2.0000 2.8284
城市距离(曼哈顿距离)
城市街区距离(City Block distance),实际上对应的是向量间的L1距离。
例子:计算向量(0,0)、(1,0)、(0,2)两两间的曼哈顿距离
X = [0 0 ; 1 0 ; 0 2]
D = pdist(X, 'cityblock')
D =
1 2 3
闵可夫斯基距离
闵氏距离不是一种距离,而是一组距离的定义。

其中p是一个变参数。
当p=1时,就是曼哈顿距离
当p=2时,就是欧氏距离
当p→∞时,就是切比雪夫距离
根据变参数的不同,闵氏距离可以表示一类的距离。
这实际上就是通常意义上的向量范数的定义。
闵氏距离,包括曼哈顿距离、欧氏距离和切比雪夫距离都存在明显的缺点。
举个例子:二维样本(身高,体重),其中身高范围是150~190,体重范围是50~60,有三个样本:a(180,50),b(190,50),c(180,60)。那么a与b之间的闵氏距离(无论是曼哈顿距离、欧氏距离或切比雪夫距离)等于a与c之间的闵氏距离,但是身高的10cm真的等价于体重的10kg么?因此用闵氏距离来衡量这些样本间的相似度很有问题。
简单说来,闵氏距离的缺点主要有两个:(1)将各个分量的量纲(scale),也就是“单位”,当作相同的看待了。(2)没有考虑各个分量的分布(期望,方差等)可能是不同的。
例子:计算向量(0,0)、(1,0)、(0,2)两两间的闵氏距离(以变参数为2的欧氏距离为例)
X = [0 0 ; 1 0 ; 0 2]
D = pdist(X,'minkowski',2)
D =
1.0000 2.0000 2.2361
切比雪夫距离
国际象棋玩过么?国王走一步能够移动到相邻的8个方格中的任意一个。那么国王从格子(x1,y1)走到格子(x2,y2)最少需要多少步?自己走走试试。你会发现最少步数总是max( | x2-x1 | , | y2-y1 | ) 步 。有一种类似的一种距离度量方法叫切比雪夫距离。
两个n维向量

实际上等效于:

例子:计算向量(0,0)、(1,0)、(0,2)两两间的切比雪夫距离
X = [0 0 ; 1 0 ; 0 2]
D = pdist(X, 'chebychev')
D =
1 2 2
马氏距离
有M个样本向量
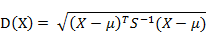
而其中向量Xi与Xj之间的马氏距离定义为:

若协方差矩阵是单位矩阵(各个样本向量之间独立同分布),则公式就成了:
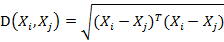
也就是欧氏距离了。
若协方差矩阵是对角矩阵,公式变成了标准化欧氏距离。
马氏距离的优点:量纲无关,排除变量之间的相关性的干扰。
例子:Matlab计算(1 2),( 1 3),( 2 2),( 3 1)两两之间的马氏距离
X = [1 2; 1 3; 2 2; 3 1]
Y = pdist(X,'mahalanobis')
Y =
2.3452 2.0000 2.3452 1.2247 2.4495 1.2247
在使用中需要注意X构成的样本需要样本个数多于维度,即X的行需要大于列才能使用。
夹角余弦
几何中夹角余弦可用来衡量两个向量方向的差异,机器学习中借用这一概念来衡量样本向量之间的差异。
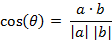
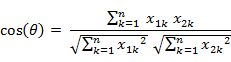
夹角余弦取值范围为[-1,1]。夹角余弦越大表示两个向量的夹角越小,夹角余弦越小表示两向量的夹角越大。当两个向量的方向重合时夹角余弦取最大值1,当两个向量的方向完全相反夹角余弦取最小值-1。
例子:计算(1,0)、( 1,1.732)、( -1,0)两两间的夹角余弦
X = [1 0 ; 1 1.732 ; -1 0]
D = 1- pdist(X, 'cosine') % Matlab中的pdist(X, 'cosine')得到的是1减夹角余弦的值
D =
0.5000 -1.0000 -0.5000
皮尔逊相关距离
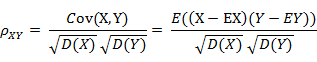
相关系数是衡量随机变量X与Y相关程度的一种方法,相关系数的取值范围是[-1,1]。相关系数的绝对值越大,则表明X与Y相关度越高。当X与Y线性相关时,相关系数取值为1(正线性相关)或-1(负线性相关)。
而相关距离的定义是1减去相关系数。
当两个变量的标准差都不为零时,相关系数才有定义,皮尔逊相关系数适用于:
(1)、两个变量之间是线性关系,都是连续数据。
(2)、两个变量的总体是正态分布,或接近正态的单峰分布。
(3)、两个变量的观测值是成对的,每对观测值之间相互独立。
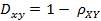
Matlab计算(1, 2 ,3 ,4 )与( 3 ,8 ,7 ,6 )之间的相关系数与相关距离
X = [1 2 3 4 ; 3 8 7 6]
C = corrcoef( X' ) %将返回相关系数矩阵
D = pdist( X , 'correlation')
如果单纯计算两个向量之间的皮尔逊相关系数,可以直接使用corr(a,b),a,b分别组织为列向量。
斯皮尔曼等级相关距离(1-斯皮尔曼等级相关系数)
在统计学中,斯皮尔曼等级相关系数以Charles Spearman命名,并经常用希腊字母ρ(rho)表示其值。斯皮尔曼等级相关系数用来估计两个变量X、Y之间的相关性,其中变量间的相关性可以使用单调函数来描述。如果两个变量取值的两个集合中均不存在相同的两个元素,那么,当其中一个变量可以表示为另一个变量的很好的单调函数时(即两个变量的变化趋势相同),两个变量之间的ρ可以达到+1或-1。
假设两个随机变量分别为X、Y(也可以看做两个集合),它们的元素个数均为N,两个随即变量取的第i(1<=i<=N)个值分别用Xi、Yi表示。对X、Y进行排序(同时为升序或降序),得到两个元素排行集合x、y,其中元素xi、yi分别为Xi在X中的排行以及Yi在Y中的排行。将集合x、y中的元素对应相减得到一个排行差分集合d,其中di=xi-yi,1<=i<=N。随机变量X、Y之间的斯皮尔曼等级相关系数可以由x、y或者d计算得到,其计算方式如下所示:
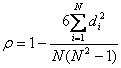
由排行集合x、y计算而得(斯皮尔曼等级相关系数同时也被认为是经过排行的两个随即变量的皮尔逊相关系数,以下实际是计算x、y的皮尔逊相关系数)(公式二):

斯皮尔曼等级相关系数对数据条件的要求没有皮尔逊相关系数严格,只要两个变量的观测值是成对的等级评定资料,或者是由连续变量观测资料转化得到的等级资料,不论两个变量的总体分布形态、样本容量的大小如何,都可以用斯皮尔曼等级相关系数来进行研究。
使用Matlab中已有的函数计算斯皮尔曼等级相关系数(使用上面的公式二):
coeff = corr(X , Y , 'type' , 'Spearman');
注意:使用Matlab自带函数计算斯皮尔曼等级相关系数时,需要保证X、Y均为列向量;Matlab自带的函数是通过公式二计算序列的斯皮尔曼等级相关系数的。
汉明距离
汉明距离的定义:两个等长字符串s1与s2之间的汉明距离定义为将其中一个变为另外一个所需要作的最小替换次数。例如字符串“1111”与“1001”之间的汉明距离为2。
应用:信息编码(为了增强容错性,应使得编码间的最小汉明距离尽可能大)。
Matlab中2个向量之间的汉明距离的定义为2个向量不同的分量所占的百分比。
例子:计算向量(0,0)、(1,0)、(0,2)两两间的汉明距离
X = [0 0 ; 1 0 ; 0 2];
D = PDIST(X, 'hamming')
D = 0.5000 0.5000 1.0000
杰卡德相似距离(1-Jaccard similarity coefficient)
两个集合A和B的交集元素在A,B的并集中所占的比例,称为两个集合的杰卡德相似系数,用符号J(A,B)表示。
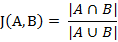
杰卡德相似系数是衡量两个集合的相似度一种指标。
与杰卡德相似系数相反的概念是杰卡德距离(Jaccard distance)。杰卡德距离可用如下公式表示:
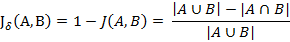
可将杰卡德相似系数用在衡量样本的相似度上。
样本A与样本B是两个n维向量,而且所有维度的取值都是0或1。例如:A(0111)和B(1011)。我们将样本看成是一个集合,1表示集合包含该元素,0表示集合不包含该元素。
p :样本A与B都是1的维度的个数
q :样本A是1,样本B是0的维度的个数
r :样本A是0,样本B是1的维度的个数
s :样本A与B都是0的维度的个数
那么样本A与B的杰卡德相似系数可以表示为:
这里p+q+r可理解为A与B的并集的元素个数,而p是A与B的交集的元素个数。
而样本A与B的杰卡德距离表示为:
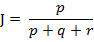
Matlab的pdist函数定义的杰卡德距离跟这里的定义有一些差别,Matlab中将其定义为不同的维度的个数占“非零维度个数”的比例,意思就是比如下面的(1,1,0)、(1,-1,0),不同的维度的个数有1个,只有第二个维度不同,两个集合中的非零元素个数为2个,1和-1嘛,所以,对应的杰卡德相似系数为0.5。
例子:计算(1,1,0)、(1,-1,0)、(-1,1,0)两两之间的杰卡德距离
X = [1 1 0; 1 -1 0; -1 1 0]
D = pdist( X , 'jaccard')
D =
0.5000 0.5000 1.0000
2015-11-07 调试记录 张朋艺




 浙公网安备 33010602011771号
浙公网安备 33010602011771号