好题——图论
前言
本文章将会持续更新,主要是一些个人觉得比较妙的题,主观性比较强(给自己记录用的),有讲错请补充。
带 !号的题是基础例题,带 * 号的是推荐首先完成的题(有一定启发性的)。
图论
最短路
P1119 灾后重建
此题看到以后以为是很简单的最短路问题(实际也不难),就写了 dijkstra ,然后光荣的 tie 了。
看数据:N 才 \(200\),想到 Floyd 算法,此题很好的利用了 Floyd 的本质,个我这种只记得模板的当头一棒。
通过其他的点进行中转来求的两点之间的最短路。我们知道,两点之间有多条路,如果换一条路可以缩短距离的话,就更新最短距离。而它最本质的思想,就是用其他的点进行中转,从而达到求出最短路的目的。
那么,如何进行中转呢?两点之间可以由一个点作为中转点更新最短路径,也可以通过多个点更新最短路径。
化解到此题:
按照时间顺序更新每一个可用的点(即修建好村庄),对于每个时间点进行两点之间询问,求对于目前建设的所有村庄来说任意两点之间的最短路
上文引用第一篇题解
void floyd(int k)
{
for(int i=0;i<n;i++)
for(int j=0;j<n;j++)
if(f[i][j]>f[i][k]+f[k][j]) f[i][j]=f[i][k]+f[k][j];
}
此题又友好的帮你把村庄的修建时间,询问的时间排好序了,用指针扫一遍就可以了,不需要每次询问都从头算一遍。
code
#include<bits/stdc++.h>
using namespace std;
const int N=200+10;
int f[N][N],a[N][N];
int ti[N],n,m,Q;
void fl(int k)
{
for(int i=0;i<n;i++)
for(int j=0;j<n;j++)
if(f[i][j]>f[i][k]+f[k][j]) f[i][j]=f[i][k]+f[k][j];
}
int main()
{
scanf("%d%d",&n,&m);
for(int i=0;i<n;i++) scanf("%d",&ti[i]);
for(int i=0;i<n;i++)
for(int j=0;j<n;j++)
f[i][j]=1e9+10;
for(int i=1;i<=n;i++)
f[i][i]=0;
for(int i=1;i<=m;i++)
{
int u,v,w;
scanf("%d%d%d",&u,&v,&w);
f[u][v]=f[v][u]=w;
}
scanf("%d",&Q);
int now=0;
while(Q--)
{
int u,v,t;
scanf("%d%d%d",&u,&v,&t);
while(now<n&&ti[now]<=t) floyd(now),now++;
if(ti[u]>t||ti[v]>t||f[u][v]==1e9+10) puts("-1");
else printf("%d\n",f[u][v]);
}
return 0;
}
! P6175 无向图的最小环问题
上题写到 floyd 的本质是:通过其他的点进行中转来求的两点之间的最短路。
而每一个点也可以成为一个环的中转点。
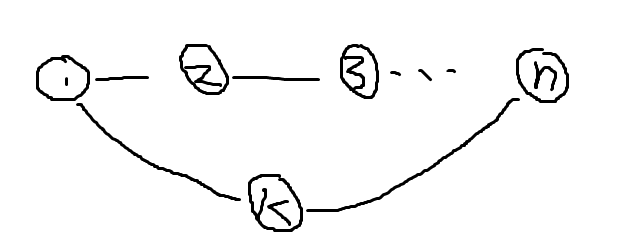
在代码上就是:
for(int k=1;k<=n;k++)
for(int i=1;i<=n;i++)
for(int j=1;j<=n;j++)
{
if(i!=j&&a[i][k]&&a[k][j])
ans=min(ans,f[i][j]+a[i][k]+a[k][j]);
f[i][j]=min(f[i][j],f[i][k]+f[k][j]);
}
又是 floyd 的一个好应用。
! P2149 [SDOI2009] Elaxia的路线
简单来说就是:无向图中,两对点间最短路的最长公共路径。
这里首先要把最短路的路径找出来,当然这个路径不止一条,然后找重叠的部分,按拓扑序求一次 dp 找最大值。
先用 dijkstra 分别从起点、终点开始跑一次单元最短路,然后一条边一条边的比对,看是否从起点到这条边加上从终点到这条边在加上这条边的边权,是否是从起点到终点的最短路(次短路也要这么写只不过是替换罢了)。
这道题是求两点对最短路的公共边,所以要跑四次单源最短路,因为路径重叠可以通向重叠也可以反向重叠,所以要跑两次 dp。
此题重在学习找最短路径是的替换思想,这在求次短路也体现了。
P5304 [GXOI/GZOI2019] 旅行者
此题标答是二进制拆分,把 \(k\) 个数按位数二进制拆分,枚举位数,这一位是 \(1\) 的放在一个集合,为 \(0\) 的放在一个集合,用一个超级源点链接第一个集合中的数,用一个超级汇点链接第二个集合中的数,跑最短路即可。时间复杂度为:\(O(Tnlog^2n)\)。
但还有一个方法是:以那 \(k\) 个数为起点与终点,正着跑一次最短路,反着跑一次最短路,然后枚举边来判断最短路,其实就是上面讲的替换思想,只不过这里不是替换,而是枚举判断多源最短路。这里要注意最后枚举时要判断是否是环。
有向图通达性:强连通分量
P7737 [NOI2021] 庆典
本题有些毒瘤,但作为 noi T3 没有很难(主要难在实现了)。
首先 tarjan 缩点成一个 DAG。
然后题目上有这个性质:对于三座城市 \(x\),\(y\),\(z\),若 \(x\Rightarrow z\) 且 \(y\Rightarrow z\),那么有 \(x\Rightarrow y\) 或 \(y\Rightarrow x\)。
说明如果一个点的入度大于一,一定会有两条路可到达这个点。
那我们只保留经过点数最多的路径,也就是拓扑排序留下的最后一条边。

把除红边都删除不影响连通性。
由于每个点都只有一个入度,所以构成了一颗有向树。
设 \(T_x\) 为 \(x\) 的子树,\(suf_x\) 为从根到 \(x\) 路径上的点集。
对于每次询问 \(s,t\),求的就是 \(suf_t\) 并上 \(T_s\)。
考虑添加一条边 \((u,v)\),设从 \(s\) 延伸出的点集为 \(A\),从 \(t\) 延伸出的点集为 \(B\):
-
如果 \(u \in A\),\(A\) 并上 \(T_v\)。
-
如果 \(v \in B\),\(B\) 并上 \(suf_u\)。
最后 \(A,B\) 求并就可以了。
求并方法为:
\(B\) 是到根路径的并,方便直接在树剖上标记,而 \(A\) 是子树的并,子树的修改也比较容易,这里只用把子树的左端 dfn 序从小到大排序,右端从大到小排序,相当与找几个独立的子树求并,树剖计算即可。
欧拉图
一些定理:
-
对于一个无向图 \(G\) 可以一笔画成的充要条件是: \(G\) 是联通的,并且奇顶点个数等于 \(0\) 或 \(2\)。当且仅当奇顶点个数为 \(0\) 时,\(G\) 是一个圈。
-
如果无向连通图有 \(G\) 有 \(2k\) 个奇顶点,则图 \(G\) 可以用 \(k\) 笔画成,并且至少要用 \(k\) 笔画成。
-
有向图 \(G\) 是欧拉图,当且仅当 \(G\) 弱连通且 \(G\) 的每个点的入度等于出度,有向图 \(G\) 是半欧拉图,当且仅当 \(G\) 弱连通,存在两个点的入度分别等于出度减 \(1\) 和出度加 \(1\),且其余每个点的入度等于出度。
例题:
! P1341 无序字母对
差分约束
*出纳员问题
注:此题解法全部引用冯威的集训队论文的文字,有兴趣观看全文。
设 \(num[ i ]\) 为 \(i\) 时刻能够开始工作的人数,\(x[ i ]\) 为实际雇佣的人数,那么 $ x[ I ]<=num[ I ]$ 。
设 \(r[ i ]\) 为 \(i\) 时刻至少需要工作的人数,于是有如下关系:
设 \(s[ I ]=x[ 1 ]+x[ 2 ]…+x[ I ]\) ,得到
对于以上的几组不等式,我们采用一种非常笨拙的办法处理这一系列的不等式(其实也是让零乱的式子变得更加整齐,易于处理)。首先我们要明白差分约束系统的应用对象(它通常针对多个二项相减的不等式的)于是我们将上面的所有式子都转化成两项未知项在左边,另外的常数项在右边,且中间用 \(\ge\) 连接的式子,即:
这里出现了小的困难,我们发现以上式子并不是标准的差分约束系统,因为在最后一个式子中出现了三个未知单位。但是注意到其中跟随 \(I\) 变化的只有两个,于是 \(s[23]\) 就变得特殊起来,看来是需要我们单独处理,于是我们把 \(s[ 23 ]\) 当作已知量放在右边。
经过这样的整理,整个图就很容易创建了,将所有形如 \(A-B>=C\) 的式子 我们从节点 \(B\) 引出一条有向边指向 \(A\) 边的权值为 \(C\)(这里注意由于左右确定,式子又是统一的>=的不等式,所以A和B是相对确定的,边是一定是指向 \(A\) 的),图就建成了 。
最后枚举所有 \(s[ 23 ]\) 的可能值,对于每一个 \(s[23]\) ,我们都进行一次常规差分约束系统问题的求解,判断这种情况是否可行,如果可行求出需要的最优值,记录到 \(Ans\) 中,最后的 \(Ans\) 的值即为所求。



 浙公网安备 33010602011771号
浙公网安备 33010602011771号