十一、进制

1、进制介绍

进制：指进位制，是人们规定的一种进位方式

常见进制：二进制、八进制、十进制、十六进制

十进制是逢十进一，二进制就是逢二进一，八进制是逢八进一…

常见进制：二进制，八进制，十进制，十六进制

2、二进制

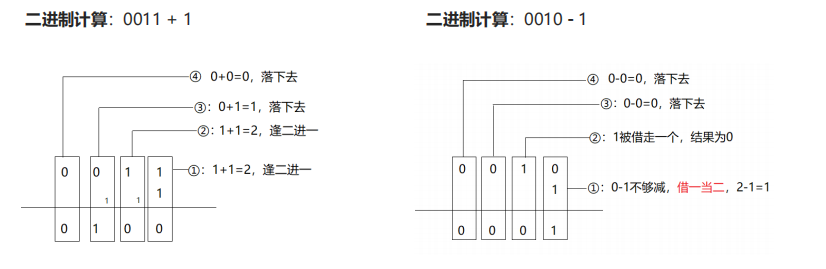
介绍：二进制数据是0和1两个数码来表示。例如：00101000。

进位规则是“逢二进一”，借位规则是“借一当二”。

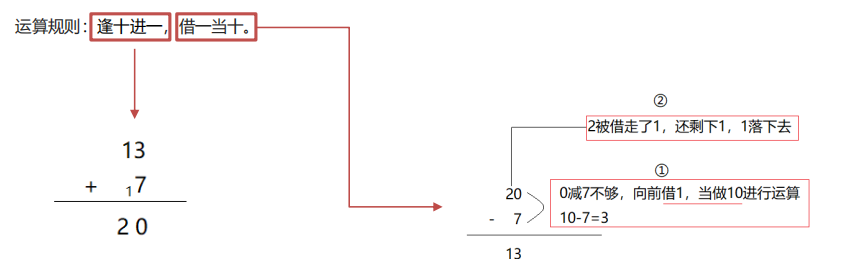
3、十进制

4、八进制和十六进制

• 八进制介绍：采用0，1，2，3，4，5，6，7八个数字，逢八进1

• 十六进制介绍：用数字0到9和字母A到F（或a_{f）表示，其中:A}F表示10~15，这些称作十六进制。

  【0】【1】【2】【3】【4】【5】【6】【7】【8】【9】【a】【b】【c】【d】【e】【f】

5、不同进制书写

10 十进制，不进行修饰

0b1000 1100 二进制，用0b修饰

077 八进制，用0修饰

0xf102a 十六进制，用0x修饰

6、任意进制转十进制

• 公式：系数 * 基数的权次幂 相加
  • 系数：每一【位】上的数
  • 基数：几进制，就是几
  • 权从数值的右侧，以 0 开始，逐个 +1 增加

二进制转十进制

十六进制转十进制

7、十进制转任意进制

• 公式：除基取余

使用源数据，不断的除以基础（几进制，基数就是几）得到余数，直到商为0，再将余数倒着拼起来即可。

十进制转二进制

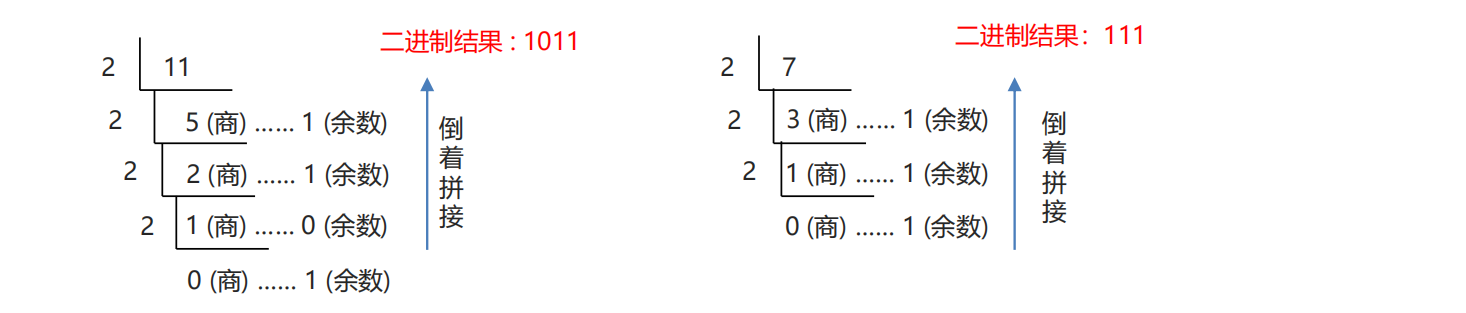
十进制转十六进制

8、快速进制转换法

8.1、8421码

• 8421码又称BCD码，是BCD码中最常用的一种
• BCD: (Binary-Coded Decimal) 二进制码十进制数
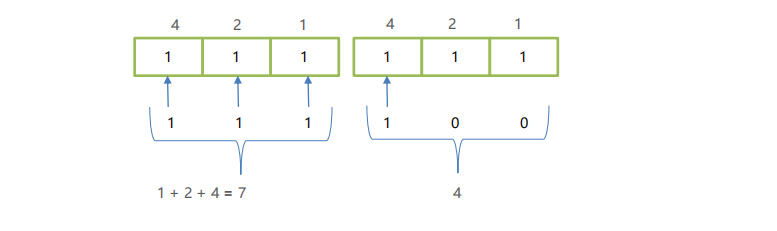
• 在这中编码方式中，每一位二进制值的1都是代表一个固定数值，把每一位的1代表的十进制数加起来得到的结果就是它所代表的十进制数。

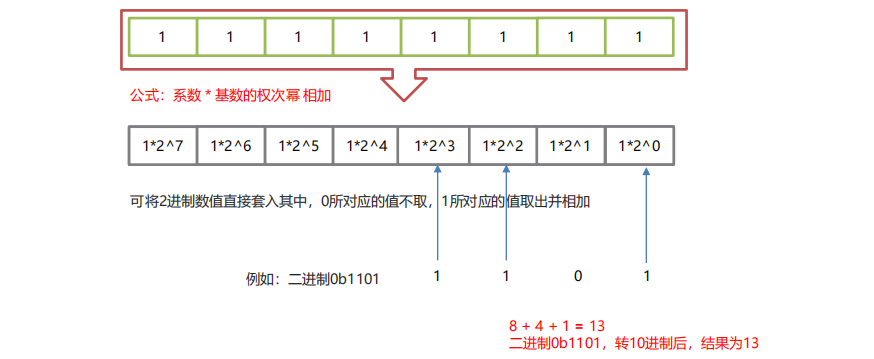
8.2、二进制快速转十进制

8.2、二进制快速转八进制

• 八进制：将三个二进制位看为一组，在进行转换

• 原因：八进制逢八进一，三个二进制位最多可以表示111，也就是7，如果出现第四位，就超范围了

• 需求：将60的二进制 0b111100 转换为八进制

8.4、二进制快速转十六进制

• 十六进制：将四个二进制位看为一组，在进行转换

• 原因：十六进制逢十六进一，四个二进制位最多可以表示1111，也就是15，如果出现第五位，就超范围了

• 需求：将60的二进制 0b111100 转换为十六进制

9、原码反码补码

9.1、介绍

注意：计算机中的数据，都是以二进制补码的形式在运算，二补码则是通过反码和原码推算出来的

• 原码（可直观看出数据大小）

  就是二进制定点表示法，即最高为符号位，【0】表示正，【1】表示负，其余位表示数值的大小。

  通过一个字节表示 +7 和 -7，代码：byte b1= 7；byte b2 = -7;

  一个字节等于8个比特位，也就是8个二进制位

  ​ 0(符号位) 0000111

  ​ 1(符号位) 0000111

• 反码：正数的反码与其原码相同；负数的反码是对其原码逐位取反，但符号位除外。

• 补码（数据以该状态进行运算）

  正数的补码与其原码相同；负数的补码是在其反码的末位加1

总结：

• 正数的原反补都是相同的
• 负数的【反码】，是根据【原码】取反（0变1,1变0）得到的。（符号位不变）
• 负数的【补码】，是根据【反码】的末尾+1，得到的

9.2、求 -7 的补码

10、位运算

10.1、位运算介绍

• 位运算符指的是二进制位的运算，先将十进制数转成二进制后在进行运算
• 在二进制位运算中，1表示 true，0表示 false。

符号	计算方式
& 与	遇0则0；两边同时为1，结果才是1
| 或	遇1则1；两边同时为0，结果才是0
^ 异或	相同为0，不同为1
~ 取反	取反，二进制位全部取反，0变1,1变0，包括符号位
<<	有符号左移运算，左边符号位丢弃，右边补齐0
>>	有符号右移运算，根据符号位，补齐左边
>>>	无符号右移，无论最符号位是0还是1，都补0

10.2、异或运算的特点

一个数，被另外一个数，异或两次，该数本身不变

案例：

已知两个整数变量a = 10，b=20，使用程序实现这两个变量的数据交换，不允许使用三方变量

public static void main(String[] args){
    int a = 10;
    int b = 20;
    a = a ^ b;  // a = 10 ^ 20;
    b = a ^ b;	// b = 10 ^ 20 ^ 20;
    a = a ^ b;  // a = 10 ^ 20 ^ 10;
    System.out.println(a);
    System.out.println(b);
}

案例：数组反转

int[] arr = {19,25,36,47,58};
int temp;

for(int start = 0,end = arr.length-1 ; start<end ; start++,end--){
    arr[start] = arr[end] ^ arr[start];
    arr[end] = arr[start] ^ arr[end];
    arr[start] = arr[start] ^ arr[end];
}

System.out.println(Arrays.toString(arr));