Boosting算法1------AdaBoost

***********************算法    https://blog.csdn.net/zwqjoy/article/details/80424783   ********************************8

boosting(提升)是一族可将弱学习器提升为强学习器的算法。提升算法的基本思想是 对于一个复杂的任务，将多个专家的判断总和得出的结果要比任何一个专家单独的判断好。

这类 算法的工作机制是   先从初始训练集中训练出一个基学习器，再根据学习器表现对训练样本分布进行调整，是对先前基学习器做错的样本再后续的样本收到更多的关注。也就是说赋予做错的样本更大的权重。然后基于调整的样本分布来训练下一个基学习器，一直反复 进行，直至达到指定值。

AdaBoost算法

AdaBoost  Adaptive Boosting的缩写，对于弱分类器的组合，AdaBoost算法采取加权多数表决的方法。

具体的说法就是加大分类误差率小的弱分类器的权重，使其在表决中起到较大的作用。缩小分类误差较大的弱分类器的权值，使其在表决中起较小的作用。

adaboost系列主要解决了  

两类问题   多类单标签的问题   多累多标签   大类单标签  回归问题

1   为数据集里的每个样本赋予相同的权重（一般情况），然后开始依据一定的分类标准来对该数据集分类，从而得到第一个Classifier[1]（弱分类器）。同时由此可得此次分类中被分错的样本，提高他们的权重，用于下一个Classifier[2]的训练。

2  依据上一次classifier训练更新样本的样本集，来训练下一个classifier。其中可以依据样本权重来影响此次训练的错误率来时此次classifier足够重视之前错分的样本。

3. 为1、2步中得到的Classifier[i]确定在最终的强分类器中的权重（此权重的确定也可以在1、2步中确定）。Strong_Classifier = ∑（ weight[i] *Classifier[i]）（弱分类器的线性组合），计算Strong_Classifier的错误率，然后综合考虑程序迭代次数来判断是否继续重复1-3步迭代训练。

 

关于adaboost的权重

adaboost算法中有两权重，一个是数据的权重，一个是弱分类器的权重。其中，数据的权重主要用于弱分类器寻找其分类误差最小的决策点。分类器权重越大则说明该分类器在最终决策时拥有更大的发言权。

1  数据的权重

刚刚已经介绍了单层决策树的原理，这里有一个问题，如果训练数据保持不变，那么单层决策树找到的最佳决策点每一次必然都是一样的，为什么呢？因为单层决策树是把所有可能的决策点都找了一遍然后选择了最好的，如果训练数据不变，那么每次找到的最好的点当然都是同一个点了。

这里adaboost数据的权重主要用于弱分类器寻找其分类误差最小的点。

举个例子，在以前没有权重时（其实是平局权重时），一共10个点时，对应每个点的权重都是0.1，分错1个，错误率就加0.1；分错3个，错误率就是0.3。现在，每个点的权重不一样了，还是10个点，权重依次是[0.01,0.01,0.01,0.01,0.01,0.01, 0.01,0.01,0.01,0.91]，如果分错了第1一个点，那么错误率是0.01，如果分错了第3个点，那么错误率是0.01，要是分错了最后一个点，那么错误率就是0.91。这样，在选择决策点的时候自然是要尽量把权重大的点（本例中是最后一个点）分对才能降低误差率。由此可见，权重分布影响着单层决策树决策点的选择，权重大的点得到更多的关注，权重小的点得到更少的关注。

每训练完一个弱分类器就会调整权重，上一轮训练中被误分类的点的权重就会增加。在本轮训练中，由于权重影响，本轮的弱分类器将更有可能把上一轮的误分类点分对，如果还是没有分对，那么分错的点的权重将继续增加，下一个弱分类器将更加关注这个点，尽量将其分对。

2  adaboost分类器的权重

由于adaboost中若干个分类器的关系是   第N个分类器更可能对第N-1个分类器没分对的数据，而不能保证以前分对的数据也能同时分对。所以在adaboost中，每个弱分类器都有各自最关注的点。，每个弱分类器都只关注整个数据集中的一部分，所以他们必然是共同组合在一起才能发挥其作用。所以最终投票表决时，需要根据弱分类器的权重来进行加权投票，权重大小是根据弱分类器的分类错误率统计算出，弱分类器错误率越低，其权重就越高。

 

 

 

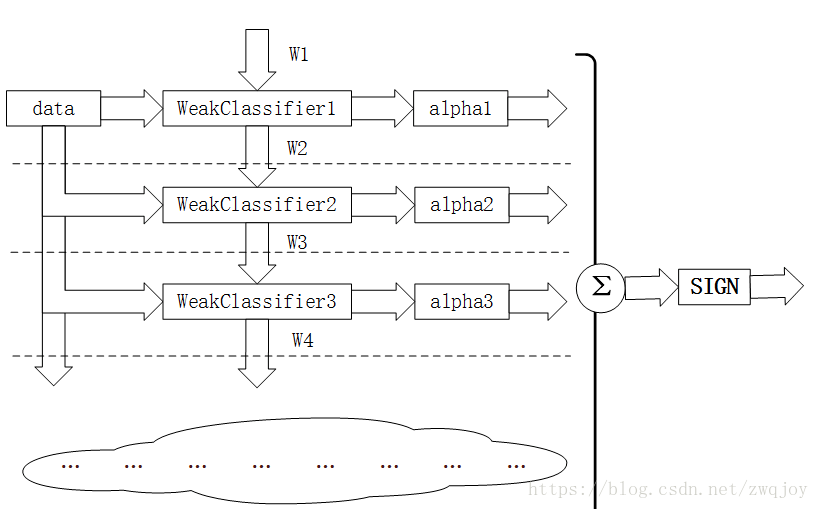
第i轮迭代要做的几件事

1  新增弱分类器weakclassifier-i与弱分类器权重alpha-i

2   通过数据集data与数据权重w-i训练弱分类器weakclassifier-i，并得出其分类错误率，以此计算出其弱分类权重alpha-i

3  通过加权投票表决的方法，让所有弱分类器进行加权投票表决得到最终预测输出，计算最终的分类错误率，如果最终的分类错误率低于阈值，则迭代结束，否则更新数据权重w-i+1