熵 交叉熵 kl散度的关系
1 三者的关系
kl散度=交叉熵-熵
熵 可以表示一个事件A的自信息量,也就是事件A包含多少信息
kl散度 可以用来表示从事件A的角度来看,事件B有多大的不同,适用于衡量ab之间的差异
交叉熵 可以从来表示从事件A的角度来看,如果描述事件B,适用于衡量不同事件B之间的差异。
对于不同的事件B,计算AB的kl散度时都同时需要减去事件A的熵,kl=交叉熵-熵(A) 因此比较不同B事件之间的差异,计算交叉熵和计算KL散度是等价的。
2 熵的公式
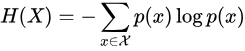
其中p(x)表示x事件发生的概率。
3 交叉熵
可以理解为 对于真实分布p,和任意非真实分布q,使用分布Q表征分布P的平均编码长度叫交叉熵。
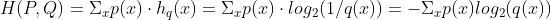
当q和p无限接近时,交叉熵方程取得最小值。
交叉熵就是用来衡量用特定的编码方案Q(模型输出结果)来对真实分布P的信息X进行编码时需要的做少bits数。
4 kl散度或者相对熵
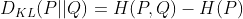
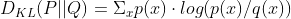
由于交叉熵一定大于信息熵,所以kl散度一定大于0.
kl散度性质 1 当p和q相同时,kl散度为0 2 kl散度不具有对称性 3 kl散度非负。
kl散度也就是 真值分布的熵与KL散度的和,而真值的熵是确定的,与模型的参数Θ无关的,所以梯度下降求导时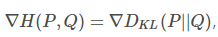 也就是说最小化交叉熵与最小化kl散度是一样的。
也就是说最小化交叉熵与最小化kl散度是一样的。
5 最大似然估计
机器学习中,通过最大似然估计方法使得参数为Θ^的模型使预测值贴近真实值的概率最大化,在实际操作中, 由于连乘很容易出现最大值或者最小值溢出,造成计算不稳定。由于log函数的单调性,所以将上式进行取对数 +取负数,最小化负对数似然的结果与原来的式子是一样的结果。即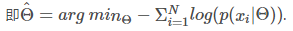




 浙公网安备 33010602011771号
浙公网安备 33010602011771号