特征工程系列：特征预处理(上)

---------------------   https://www.cnblogs.com/purple5252/p/11343809.html   -----------

前言  

数据和特征决定了机器学习的上限，而模型和算法知识逼近这个上限而已。

特征工程在机器学习中占有非常重要的地位。

特征工程EDA(探索性数据分析) 数据预处理 特征提取  特征选择  特征构造等子问题  ，数据预处理又包括了数据清洗和特征预处理等子问题。

1  数值型特征无量纲化

无量纲化使不同规则的数据转换到同一个规格，常见的无量纲化方法有标准化和归一化。

1.1    数据标准化   Z-Score

标准化的前提是特征值服从正态分布，标准化后，其转换成标准正态分布。

标准化公式为  

 

 

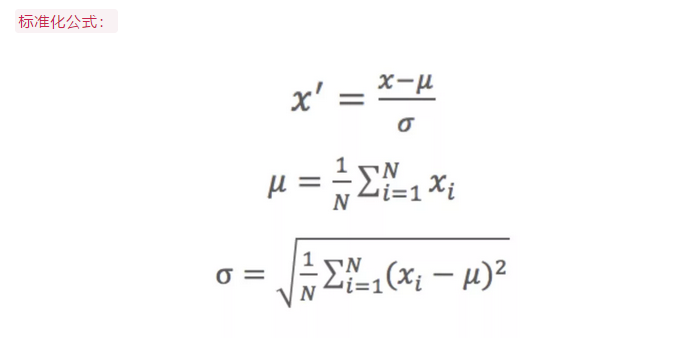
1.2    归一化

1.2.1   MinMax归一化

 

 

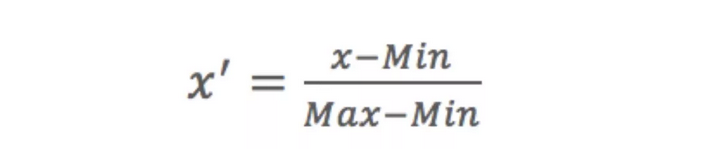
1.2.2   MaxAbs归一化

 

 

 

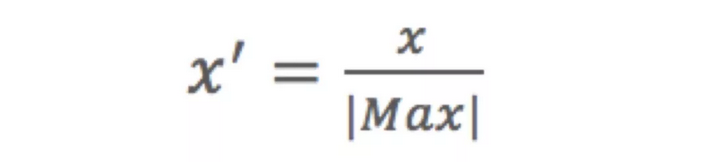
1.3    正态分布化

Normalization主要思想是对每个样本计算p范数，然后对该样本中的每个元素除以该范数，这样处理的结果是使得每个处理后的样本的p范数等于1.

 

1.4    标准化和归一化对比

都是一种线性变换，都可以取消由于不同量纲不同引起的误差。都是对向量X按照比例压缩再进行平移。

不同：

1 目的不同，归一化是为了消除量纲压缩到01 区间

标准化只是调整特征整体的分布

归一化和最大 最小化有关。

标准化与均值 标准差有关。

归一化输出在01之间。

标准化无限制。

1 什么时候使用归一化 什么时候用标准化

如果对输出结果范围有要求，用归一化

如果数据较为稳定，不存在极端的最大最小值，用归一化

如果数据存在异常值和较多噪音，用标准化，可以间接通过中心化避免异常值和极端值的影响。

 

除了上面介绍的一些方法之外，还有RobustScaler  PowerTransformer  QuantileTransformer 和QuantileTransformer等方法。

 

2 数值型特征分箱

离散化是数值型特征非常重要的一个处理，其实就是要讲数值数据转化成类型数据，连续值的取值空间可能是无穷，为了便于表示和在模型中处理，需要对连续值特征进行离散化处理。

1  无监督分箱法

1.1  自定义分箱

1.2 等距分箱

1.3  等频分箱    

将数据分成几等分，每等分数据里的个数是一样的。区间的边界值要经过选择，使得每个分区包含大致相等的实例数量。比如说 N=10 ,每个区间应该包含大约10%的实例。

df['age_bin']=pd.qcut(df['age'],3)

1.4  聚类分箱

1.5  二值化

将数值型的特征进行阈值化得到boolean型数据，这对于下游的概率估计可能很有用。

代码实现：

from sklearn.preprocessing  import  binarizer

binarizer=Binarizer(threshold ).fit(x_train)

binarizer.transform(x_train)

2  有监督分箱法

2.1  卡方分箱法

-------  卡方相关资料    https://blog.csdn.net/dta0502/article/details/82317969   ------------

 -------------相关资料    https://blog.csdn.net/troysps/article/details/104037176  -------------

对于精确的离散化，相对类频率在一个区间内应当完全一致，因此，如果两个相邻的区间具有非常类似的类分布，则这两个区间可以合并，否则，他们应当保持分开，而底卡方值表明他们具有相似的类分布。

2.2  最小熵法分箱

需要使总熵值达到最小，也就是使分箱能够最大限度地区分因变量的各类别。

熵是信息论中数据无序程度的度量标准，提出信息熵的基本目的是找出某种符号系统的信息量和冗余度之间的关系，以便能用最小的成本和消耗来实现最高效率的数据存储、管理和传递。
数据集的熵越低，说明数据之间的差异越小，最小熵划分就是为了使每箱中的数据具有最好的相似性。给定箱的个数，如果考虑所有可能的分箱情况，最小熵方法得到的箱应该是具有最小熵的分箱。