二叉树

任何一颗二叉树的叶子结点在先序、中序、后序遍历序列中的相对次序是不发生改变的，因为根据三个遍历的次序和特点：前序是根左右、中序是左根右、后序是左右根,因此相对次序发生变化的都是子树的根,也就是分支结点。

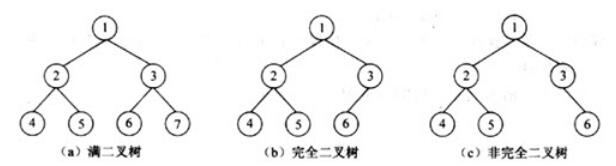
根据其定义，一棵完全二叉树除了最后一层外，其余层的节点数都是满的，最后一层的节点也必须自左至右排列，例如图(a)是高度为3的满二叉树，图(b)是完全二叉树，图(c)不是完全二叉树。

 

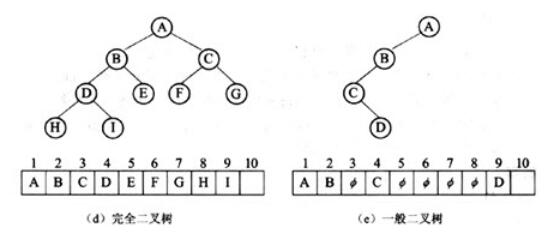
二叉树采用顺序存储结构时，对于编号为i的节点，则有：

● 若i=l时，该节点为根节点，无双亲：

● 若i＞l时，该节点的双亲节点为|i/2|：

● 若2i≤n，则该节点的左孩子编号为2i否则无左孩子：

● 若2i+1≤n，则该节点的右孩子编号为2i+1，否则无右孩子。

图(d)为具有10个节点的完全二叉树及其顺序存储结构，图(e)为某非完全二叉树的顺序存储结构，从中可以看出，完全二叉树适合采用顺序存储结构。

 

可以推导出具有n个节点的完全二叉树的深度为[log2n]+1。

 

 

　　一个连通图的生成树是一个极小连通子图，它包含图中的全部顶点，但只有构成一棵树的n-1条边。把生成树各边的权值总和称为生成树的权，把权值最小的生成树称为最小生成树。

　　 哈夫曼树又称最优二叉树，是一类带权路径长度最短的树。若深度为k的二叉树有2k-1个结点，则称其为满二叉树。可以对满二叉树中的结点进行连续编号:约定编号从根结点起，自上而下、自左至右依次进行。深度为k、有n个结点的二叉树，当且仅当其每一个结点都与深度为k的满二叉树中编号从1至n的结点一一对应时，称之为完全二叉树。

　　二叉排序树又称二叉查找树，它或者是一棵空树，或者是具有如下性质的二叉树。

　　若它的左子树非空，则左子树上所有结点的值均小于根结点的值。

　　若它的右子树非空，则右子树上所有结点的值均大于根结点的值。

　　显然，将一个无序序列中的元素依次插入到一棵二叉排序树中并进行中序遍历，可得到一个有序序列。