线性代数

标量、向量、矩阵和张量

转置（transpose）是矩阵的重要操作之一。矩阵的转置是以对角线为轴的镜像，这条从左上角到右下角的对角线被称为主对角线（main diagonal）。

我们将矩阵A的转置表示为：（就是行转为列）

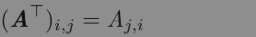
只要矩阵的形状一样，我们可以把两个矩阵相加。两个矩阵相加是指对应位置的元素相加，比如C=A+B，其中Ci,j=Ai,j+Bi,j。
标量和矩阵相乘，或是和矩阵相加时，我们只需将其与矩阵的每个元素相乘或相加，比如D=a·B+c，其中Di,j=a·Bi,j+c。
在深度学习中，我们也使用一些不那么常规的符号。我们允许矩阵和向量相加，产生另一个矩阵：C=A+b，其中Ci,j=Ai,j+bj。换言之，向量b和矩阵A的每一行相加。这种隐式地复制向量b到很多位置的方式，称为广播(broadcasting)。

矩阵和向量相乘

为了使乘法可被定义，矩阵A的列数必须和矩阵B的行数相等。如果矩阵A的形状是m×n，矩阵B的形状是n×p，那么矩阵C的形状是m×p。我们可以通过将两个或多个矩阵并列放置以书写矩阵乘法，例如：

该乘法操作定义为：

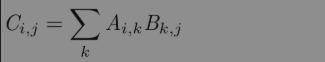
两个相同维数的向量x和y的点积（dot product）可看作矩阵乘积[插图]。我们可以把矩阵乘积C=AB中计算Ci,j的步骤看作A的第i行和B的第j列之间的点积。（点积就是对应元素相乘，乘积就是矩阵乘法）

矩阵乘积服从分配律：

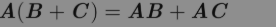
矩阵乘积服从结合律：

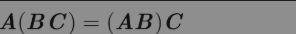
不同于标量乘积，矩阵乘积并不满足交换律（AB=BA的情况并非总是满足）。然而，两个向量的点积满足交换律：

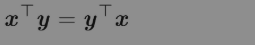
矩阵乘积的转置有着简单的形式：

利用两个向量点积的结果是标量、标量转置是自身的事实，我们可以证明：

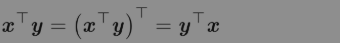
单位矩阵和逆矩阵

单位矩阵：任意向量和单位矩阵相乘，都不会改变。我们将保持n维向量不变的单位矩阵记作In。单位矩阵的结构很简单：所有沿主对角线的元素都是1，而其他位置的所有元素都是0。

矩阵A的矩阵逆记作A^-1，其定义的矩阵满足如下条件：

现在我们可以通过以下步骤求解式：

这取决于我们能否找到一个逆矩阵A-1。

逆矩阵A^-1主要是作为理论工具使用的，并不会在大多数软件应用程序中实际使用。这是因为逆矩阵A-1在数字计算机上只能表现出有限的精度，有效使用向量b的算法通常可以得到更精确的x。

线性相关和生成子空间

对于Ax=b，如果A^-1存在，那么每一个向量b恰好存在一个解，否则有可能不存在解或者存在无限多个解（不可能存在多于一个少于无限多个情况）；因为如果x和y都是某方程组的解，则：（其中α取任意实数也是该方程组的解）

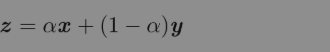
为了分析方程有多少个解，我们可以将A的列向量看作从原点（origin）（元素都是零的向量）出发的不同方向，确定有多少种方法可以到达向量b。在这个观点下，向量x中的每个元素表示我们应该沿着这些方向走多远，即xi表示我们需要沿着第i个向量的方向走多远：

一般而言，这种操作称为线性组合（linear combination）。形式上，一组向量的线性组合，是指每个向量乘以对应标量系数之后的和，即：

一组向量的生成子空间（span）是原始向量线性组合后所能抵达的点的集合。确定Ax=b是否有解，相当于确定向量b是否在A列向量的生成子空间中。这个特殊的生成子空间被称为A的列空间（column space）或者A的值域（range）。

如果一组向量中的任意一个向量都不能表示成其他向量的线性组合，那么这组向量称为线性无关（linearly independent）。如果某个向量是一组向量中某些向量的线性组合，那么我们将这个向量加入这组向量后不会增加这组向量的生成子空间。

矩阵可逆，意味着该矩阵必须是一个方阵（square），即m=n，并且所有列向量都是线性无关的。一个列向量线性相关的方阵被称为奇异的（singular）。如果矩阵A不是一个方阵或者是一个奇异的方阵，该方程仍然可能有解。但是我们不能使用矩阵逆去求解。对于方阵而言，它的左逆和右逆是相等的（A^-1A=AA^-1=I）

范数

有时我们需要衡量一个向量的大小。在机器学习中，我们经常使用称为范数（norm）的函数来衡量向量大小。形式上，Lp范数定义如下：

其中p∈R,p≥1。

范数（包括Lp范数）是将向量映射到非负值的函数。直观上来说，向量x的范数衡量从原点到点x的距离。更严格地说，范数是满足下列性质的任意函数：

f(x)=0⇒x=0;
f(x+y)≤f(x)+f(y)（三角不等式（triangle inequality））;
f(αx)=|α|f(x)。

当p=2时，L2范数称为欧几里得范数（Euclidean norm）。它表示从原点出发到向量x确定的点的欧几里得距离。平方L2范数也经常用来衡量向量的大小，可以简单地通过点积 x^Tx 计算。

平方L2范数在数学和计算上都比L2范数本身更方便。例如，平方L2范数对x中每个元素的导数只取决于对应的元素，而L2范数对每个元素的导数和整个向量相关。但是在很多情况下，平方L2范数也可能不受欢迎，因为它在原点附近增长得十分缓慢。在某些机器学习应用中，区分恰好是零的元素和非零但值很小的元素是很重要的。在这些情况下，我们转而使用在各个位置斜率相同，同时保持简单的数学形式的函数：L1范数。L1范数可以简化如下:

L1范数经常作为表示非零元素数目的替代函数。

另外一个经常在机器学习中出现的范数是L∞范数，也被称为最大范数（max norm）。这个范数表示向量中具有最大幅值的元素的绝对值：

有时候我们可能也希望衡量矩阵的大小。在深度学习中，最常见的做法是使用Frobenius范数（Frobenius norm），即：

两个向量的点积可以用范数来表示，具体如下：（θ表示x和y之间的夹角）

特殊类型的矩阵和向量

对角矩阵（diagonal matrix）只在主对角线上含有非零元素，其他位置都是零。对角矩阵受到关注的部分原因是对角矩阵的乘法计算很高；计算乘法diag（v）x，我们只需要将x中的每个元素xi放大vi倍。换言之，diag（v）x=v⊙x。对角方阵的逆矩阵存在，当且仅当对角元素都是非零值，在这种情况下，diag(v)^-1 = diag([1/v₁,……,1/v_n]^T)。非方阵的对角矩阵没有逆矩阵，对于一个长方形对角矩阵D而言，乘法Dx会涉及x中每个元素的缩放，如果D是瘦长型矩阵，那么在缩放后的末尾添加一些零；如果D是胖宽型矩阵，那么在缩放后去掉最后一些元素。
对称（symmetric）矩阵是转置和自己相等的矩阵，即：
单位向量（unit vector）是具有单位范数（unit norm）的向量，即：
如果 x^Ty=0，那么向量x和向量y互相正交（orthogonal）。如果两个向量都有非零范数，那么这两个向量之间的夹角是90◦。在Rn中，至多有n个范数非零向量互相正交。如果这些向量不但互相正交，而且范数都为1，那么我们称它们是标准正交（orthonormal）。
正交矩阵（orthogonal matrix）指行向量和列向量是分别标准正交的方阵，即：

这意味着：

特征分解

特征分解（eigendecomposition）是使用最广的矩阵分解之一，即我们将矩阵分解成一组特征向量和特征值。
方阵A的特征向量（eigenvector）是指与A相乘后相当于对该向量进行缩放的非零向量v：

其中标量λ称为这个特征向量对应的特征值（eigenvalue）。如果v是A的特征向量，那么任何缩放后的向量 sv 也是A的特征向量。此外，sv和v有相同的特征值。基于这个原因，通常我们只考虑单位特征向量。
假设矩阵A有n个线性无关的特征向量{v⁽¹⁾,···,v⁽ⁿ⁾}，对应着特征值{λ₁,···,λ_n}。我们将特征向量连接成一个矩阵，使得每一列是一个特征向量：V=[v(1),···,v(n)]。类似地，我们也可以将特征值连接成一个向量 λ=[λ₁,…,λ_n]^T 。因此A的特征分解（eigendecomposition）可以记作:
我们也常常希望将矩阵分解（decompose）成特征值和特征向量。不是每一个矩阵都可以分解成特征值和特征向量。在某些情况下，特征分解存在，但是会涉及复数而非实数。在本书中，我们通常只需要分解一类有简单分解的矩阵。具体来讲，每个实对称矩阵都可以分解成实特征向量和实特征值：

其中Q是A的特征向量组成的正交矩阵，Λ是对角矩阵。特征值Λi,i对应的特征向量是矩阵Q的第i列，记作Q:,i。因为Q是正交矩阵，我们可以将A看作沿方向v(i)延展λi倍的空间。
矩阵的特征分解给了我们很多关于矩阵的有用信息。矩阵是奇异的，当且仅当含有零特征值。实对称矩阵的特征分解也可以用于优化二次方程f(x)=x^TAx，其中限制‖x‖₂=1。当x等于A的某个特征向量时，f将返回对应的特征值。在限制条件下，函数f的最大值是最大特征值，最小值是最小特征值。
所有特征值都是正数的矩阵称为正定（positive definite）；所有特征值都是非负数的矩阵称为半正定（positive semidefinite）。同样地，所有特征值都是负数的矩阵称为负定（negative definite）；所有特征值都是非正数的矩阵称为半负定（negative semidefinite）。半正定矩阵受到关注是因为它们保证x^TAx>=0。此外，正定矩阵还保证 x^TAx=0=>x=0。

奇异值分解

奇异值分解（singular value decomposition, SVD），是将矩阵分解为奇异向量（singular vector）和奇异值（singular value）。奇异值分解有更广泛的应用。每个实数矩阵都有一个奇异值分解，但不一定都有特征分解。例如，非方阵的矩阵没有特征分解，这时我们只能使用奇异值分解。
奇异值分解与特征分解是类似的，只不过这回我们将矩阵A分解成三个矩阵的乘积：
假设A是一个m×n的矩阵，那么U是一个m×m的矩阵，D是一个m×n的矩阵，V是一个n×n矩阵
这些矩阵中的每一个经定义后都拥有特殊的结构。矩阵U和V都定义为正交矩阵，而矩阵D定义为对角矩阵。注意，矩阵D不一定是方阵。
对角矩阵D对角线上的元素称为矩阵A的奇异值（singular value）。矩阵U的列向量称为左奇异向量（left singular vector），矩阵V的列向量称右奇异向量（right singular vector）。事实上，我们可以用与A相关的特征分解去解释A的奇异值分解。A的左奇异向量（left singular vector）是 AA^T 的特征向量。A的右奇异向量（right singular vector）是 A^TA 的特征向量。A的非零奇异值是 A^TA 特征值的平方根，同时也是 AA^T 特征值的平方根。
SVD最有用的一个性质可能是拓展矩阵求逆到非方矩阵上。

Moore-Penrose伪逆

矩阵A的伪逆定义为：
计算伪逆的实际算法没有基于这个定义，而是使用下面的公式：
- 其中，矩阵U、D和V是矩阵A奇异值分解后得到的矩阵。对角矩阵D的伪逆D+是其非零元素取倒数之后再转置得到的。
当矩阵A的列数多于行数时，使用伪逆求解线性方程是众多可能解法中的一种。特别地，x=A⁺y是方程所有可行解中欧几里得范数‖x‖2最小的一个。
当矩阵A的行数多于列数时，可能没有解。在这种情况下，通过伪逆得到的x使得Ax和y的欧几里得距离‖Ax-y‖₂最小。

迹运算
迹运算返回的是矩阵对角元素的和：
迹运算提供了另一种描述矩阵Frobenius范数的方式：
运算在转置运算下是不变的：
多个矩阵相乘得到的方阵的迹，和将这些矩阵中的最后一个挪到最前面之后相乘的迹是相同的。当然，我们需要考虑挪动之后矩阵乘积依然定义良好：
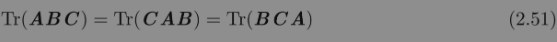
或者更一般地，
另一个有用的事实是标量在迹运算后仍然是它自己：a=Tr（a）。