堆是古往今来唯一被泱泱中华的文人骚客们题诗作赋过的数据结构。什么,看官您不信?咱可有诗为证。诗曰:
堆实际上是一棵完全二叉树。为了维持“上头尖来下头粗”的形状和有序性,我们规定老子要在儿子的上面,而且比儿子的键值要小。丫丫个呸,这简直就是大头儿子小头爸爸嘛。这样,它和二叉查找树比较起来有个好处,就是假如你想知道堆中“头”最小的爸爸是谁,压根不用找,最顶上那个就是。毛主席教导我们,看问题要一分为二。凡事有好就有坏,堆所带来的坏处就是除了可以很轻松的查找堆中最小值外,基本上不能做别的了。当然,插入和删除这种基本操作还是可以做的。
堆的插入操作就是暂时认为要插入的值是“头”最大的儿子,把它先放入最下层下一个可用位置上。然后让其与老子比较,看谁的“头”大。持续这个过程,让其一直朝着最顶层的根祖宗方向往上冒,直到找到合适位置。这个过程称为“percolate up”。
而删除操作则反其道而行之。我们知道,找到最小项很容易,难点在于如何删除它。当最小项“死亡”后,我们会发现,在根位置找不到“头”最小的祖宗了,形成了一个空结点。这还了得。为了维持“上头尖来下头粗”的形状,我们得找个祖宗放到该位置。于是我们把堆中最后一项放入空结点。如果最后一项应该放在这,操作就完成了。然而,这几乎不可能,除非堆的大小是2或3。那么只能沿着儿子结点往下移动了。但是有两个儿子哎,选哪个?废话,当然是选“头”较小的那个啦,这样才显得像父子,看见“大头”就来气。就这样,一直移动到合适位置。这个过程则称为“percolate down”。
那我们该怎么找父亲儿子呢?这就得依靠完全二叉树的特性了。完全二叉树是完全填满的树,只有最底层可能有例外。最底层按从左到右的次序填入,中间不能有空结点。如图所示:
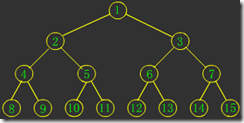 图1
图1
 图2
图2
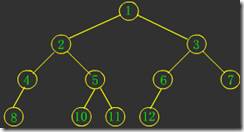 图3
图3
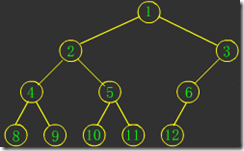 图4
图4
图1是一棵满二叉树;图2是一棵完全二叉树;图3和图4都不是完全二叉树,因为这两个中间都有空结点。很显然,满二叉树也是完全二叉树。看看图1和图2是不是很像“上头尖来下头粗”的一坨,:-)。
完全二叉树有许多有用的特性。比如,N个结点的完全二叉树的高度至多是 logN 。不需要 left 和 right 链接等。这样,我们可以将一棵完全二叉树以按层遍历的次序存储在数组中(这符合原则4)。我们把根祖宗放入数组索引 1 的位置,其他结点依次放入。为什么不放在索引 0 呢?因为除了根结点外,每个结点都有父节点。为了避免特殊情况,我们保留位置 0 为哑结点,使其可以当作根结点的父亲。此外,还有其他好处,不再一一列举。这样,我们对数组中任意索引 i 的结点,均可以在索引 2i 处找到它的左儿子。如果该位置超出了树中结点数,那我们就知道它没有左儿子。同理,它的右儿子在索引 2i+1 处。当然,我们也要测试其是否存在。它老子则在 i/2 索引处。
如果只需要插入,删除和找最小值三种操作,那么我们应该毫不犹豫的使用堆。那什么时候会有这种情况?比方说,喜欢我的MM有一个加强排。这么多人每天都围在你身边嗡嗡来嗡嗡去,咋应付啊?于是,我定个标准:每次,我都只找队伍里面最清纯的MM。这下,整个世界清净了。以后,当遇见新美女时,就把她放到队伍合适的位置。那些跟咱Say 88的MM,则一概从队伍里面开除。这个时候,这个队伍用堆来排列最合适不过。这听起来好像优先级队列啊。没错,堆还有一个别名,正是优先级队列。
很遗憾,.NET并没有提供优先级队列集合。我们只能自己编写,下面是完整源代码。

 PriorityQueue完整源码
PriorityQueue完整源码
1 using System;
using System;
2 using System.Collections.Generic;
using System.Collections.Generic;
3
4 namespace Lucifer.DataStructure
namespace Lucifer.DataStructure
5 {
{
6 public class PriorityQueue<T>
public class PriorityQueue<T>
7 {
{
8 #region 私有变量
#region 私有变量
9
10 private int theSize;
private int theSize;
11 private T[] theArray;
private T[] theArray;
12 private IComparer<T> theComparer;
private IComparer<T> theComparer;
13
14 private const int defaultCapacity = 100;
private const int defaultCapacity = 100;
15
16 #endregion
#endregion
17
18 #region 构造函数
#region 构造函数
19
20 public PriorityQueue()
public PriorityQueue()
21 : this(Comparer<T>.Default)
: this(Comparer<T>.Default)
22 {
{
23 }
}
24
25 public PriorityQueue(IComparer<T> comparer)
public PriorityQueue(IComparer<T> comparer)
26 {
{
27 this.theArray = new T[defaultCapacity];
this.theArray = new T[defaultCapacity];
28 this.theComparer = comparer;
this.theComparer = comparer;
29 }
}
30
31 public PriorityQueue(IEnumerable<T> collection)
public PriorityQueue(IEnumerable<T> collection)
32 {
{
33 this.theComparer = Comparer<T>.Default;
this.theComparer = Comparer<T>.Default;
34
35 ICollection<T> currentCollection = collection as ICollection<T>;
ICollection<T> currentCollection = collection as ICollection<T>;
36
37 if (currentCollection != null)
if (currentCollection != null)
38 {
{
39 this.theSize = currentCollection.Count;
this.theSize = currentCollection.Count;
40 this.theArray = new T[(theSize + 2) * 11 / 10];
this.theArray = new T[(theSize + 2) * 11 / 10];
41 currentCollection.CopyTo(theArray, 1);
currentCollection.CopyTo(theArray, 1);
42 }
}
43 else
else
44 {
{
45 int i = 1;
int i = 1;
46 foreach (T item in collection)
foreach (T item in collection)
47 {
{
48 this.theArray[i++] = item;
this.theArray[i++] = item;
49 theSize++;
theSize++;
50 }
}
51 }
}
52
53 this.BuildHeap();
this.BuildHeap();
54 }
}
55
56 #endregion
#endregion
57
58 #region 公有方法
#region 公有方法
59 /// <summary>
/// <summary>
60 /// 添加 item 到优先级队列中。
/// 添加 item 到优先级队列中。
61 /// </summary>
/// </summary>
62 /// <param name="item">要添加的值。</param>
/// <param name="item">要添加的值。</param>
63 public void Add(T item)
public void Add(T item)
64 {
{
65 if (theSize + 1 == theArray.Length)
if (theSize + 1 == theArray.Length)
66 {
{
67 Array.Resize<T>(ref theArray, theArray.Length == 0 ? defaultCapacity : (theArray.Length * 2));
Array.Resize<T>(ref theArray, theArray.Length == 0 ? defaultCapacity : (theArray.Length * 2));
68 }
}
69 /*
/*
70 * 向上过滤。
* 向上过滤。
71 */
*/
72 int hole = ++theSize;
int hole = ++theSize;
73 theArray[0] = item;
theArray[0] = item;
74 for (; theComparer.Compare(item, theArray[hole / 2]) < 0; hole /= 2)
for (; theComparer.Compare(item, theArray[hole / 2]) < 0; hole /= 2)
75 {
{
76 theArray[hole] = theArray[hole / 2];
theArray[hole] = theArray[hole / 2];
77 }
}
78 theArray[hole] = item;
theArray[hole] = item;
79 }
}
80
81 /// <summary>
/// <summary>
82 /// 清空优先级队列。
/// 清空优先级队列。
83 /// </summary>
/// </summary>
84 public void Clear()
public void Clear()
85 {
{
86 Array.Clear(theArray, 0, theSize);
Array.Clear(theArray, 0, theSize);
87 this.theSize = 0;
this.theSize = 0;
88 }
}
89
90 /// <summary>
/// <summary>
91 /// 移除优先级队列中最小项。
/// 移除优先级队列中最小项。
92 /// </summary>
/// </summary>
93 /// <returns>返回优先级队列中被移除的最小项。</returns>
/// <returns>返回优先级队列中被移除的最小项。</returns>
94 public T Remove()
public T Remove()
95 {
{
96 T item = this.GetMin();
T item = this.GetMin();
97 theArray[1] = theArray[theSize--];
theArray[1] = theArray[theSize--];
98 this.PercolateDown(1);
this.PercolateDown(1);
99
100 return item;
return item;
101 }
}
102
103 /// <summary>
/// <summary>
104 /// 获得优先级队列中最小项。
/// 获得优先级队列中最小项。
105 /// </summary>
/// </summary>
106 /// <returns>返回优先级队列中最小项。</returns>
/// <returns>返回优先级队列中最小项。</returns>
107 /// <exception>抛出 InvalidOperationException 异常,当队列为空时。</exception>
/// <exception>抛出 InvalidOperationException 异常,当队列为空时。</exception>
108 public T GetMin()
public T GetMin()
109 {
{
110 if (this.IsEmpty())
if (this.IsEmpty())
111 {
{
112 throw new InvalidOperationException("The queue is empty.");
throw new InvalidOperationException("The queue is empty.");
113 }
}
114
115 return theArray[1];
return theArray[1];
116 }
}
117
118 /// <summary>
/// <summary>
119 /// 判断优先级队列是否为空。
/// 判断优先级队列是否为空。
120 /// </summary>
/// </summary>
121 /// <returns>如果是空队列,返回 true 。否则,返回 false 。</returns>
/// <returns>如果是空队列,返回 true 。否则,返回 false 。</returns>
122 public bool IsEmpty()
public bool IsEmpty()
123 {
{
124 return theSize == 0;
return theSize == 0;
125 }
}
126
127 #endregion
#endregion
128
129 #region 公有属性
#region 公有属性
130
131 /// <summary>
/// <summary>
132 /// 获得优先级队列中项的数量。
/// 获得优先级队列中项的数量。
133 /// </summary>
/// </summary>
134 public int Count
public int Count
135 {
{
136 get
get
137 {
{
138 return theSize;
return theSize;
139 }
}
140 }
}
141
142 #endregion
#endregion
143
144 #region 私有方法
#region 私有方法
145 /*
/*
146 * 构造一个堆。
* 构造一个堆。
147 */
*/
148 private void BuildHeap()
private void BuildHeap()
149 {
{
150 for (int i = theSize / 2; i > 0; i--)
for (int i = theSize / 2; i > 0; i--)
151 {
{
152 this.PercolateDown(i);
this.PercolateDown(i);
153 }
}
154 }
}
155
156 /*
/*
157 * 向下过滤。
* 向下过滤。
158 */
*/
159 private void PercolateDown(int hole)
private void PercolateDown(int hole)
160 {
{
161 int child;
int child;
162 T item = theArray[hole];
T item = theArray[hole];
163 for (; hole * 2 <= theSize; hole = child)
for (; hole * 2 <= theSize; hole = child)
164 {
{
165 child = hole * 2;
child = hole * 2;
166 /*
/*
167 * 父结点并不总是有两个子结点。
* 父结点并不总是有两个子结点。
168 */
*/
169 if (child != theSize && theComparer.Compare(theArray[child + 1], theArray[child]) < 0)
if (child != theSize && theComparer.Compare(theArray[child + 1], theArray[child]) < 0)
170 {
{
171 child++;
child++;
172 }
}
173
174 if (theComparer.Compare(theArray[child], item) < 0)
if (theComparer.Compare(theArray[child], item) < 0)
175 theArray[hole] = theArray[child];
theArray[hole] = theArray[child];
176 else
else
177 break;
break;
178 }
}
179 theArray[hole] = item;
theArray[hole] = item;
180 }
}
181
182 #endregion
#endregion
183 }
}
184 }
}
此外,还有一些别的堆。比如斜堆,偶堆,斐波那契堆等,不再阐述。有兴趣的朋友可以参考其他资料。
Heap啊,Heap,
上头尖来下头粗。
有朝一日倒过来,
下头尖来上头粗。
堆实际上是一棵完全二叉树。为了维持“上头尖来下头粗”的形状和有序性,我们规定老子要在儿子的上面,而且比儿子的键值要小。丫丫个呸,这简直就是大头儿子小头爸爸嘛。这样,它和二叉查找树比较起来有个好处,就是假如你想知道堆中“头”最小的爸爸是谁,压根不用找,最顶上那个就是。毛主席教导我们,看问题要一分为二。凡事有好就有坏,堆所带来的坏处就是除了可以很轻松的查找堆中最小值外,基本上不能做别的了。当然,插入和删除这种基本操作还是可以做的。
堆的插入操作就是暂时认为要插入的值是“头”最大的儿子,把它先放入最下层下一个可用位置上。然后让其与老子比较,看谁的“头”大。持续这个过程,让其一直朝着最顶层的根祖宗方向往上冒,直到找到合适位置。这个过程称为“percolate up”。
而删除操作则反其道而行之。我们知道,找到最小项很容易,难点在于如何删除它。当最小项“死亡”后,我们会发现,在根位置找不到“头”最小的祖宗了,形成了一个空结点。这还了得。为了维持“上头尖来下头粗”的形状,我们得找个祖宗放到该位置。于是我们把堆中最后一项放入空结点。如果最后一项应该放在这,操作就完成了。然而,这几乎不可能,除非堆的大小是2或3。那么只能沿着儿子结点往下移动了。但是有两个儿子哎,选哪个?废话,当然是选“头”较小的那个啦,这样才显得像父子,看见“大头”就来气。就这样,一直移动到合适位置。这个过程则称为“percolate down”。
那我们该怎么找父亲儿子呢?这就得依靠完全二叉树的特性了。完全二叉树是完全填满的树,只有最底层可能有例外。最底层按从左到右的次序填入,中间不能有空结点。如图所示:
 图1
图1 图2
图2 图3
图3 图4
图4图1是一棵满二叉树;图2是一棵完全二叉树;图3和图4都不是完全二叉树,因为这两个中间都有空结点。很显然,满二叉树也是完全二叉树。看看图1和图2是不是很像“上头尖来下头粗”的一坨,:-)。
完全二叉树有许多有用的特性。比如,N个结点的完全二叉树的高度至多是 logN 。不需要 left 和 right 链接等。这样,我们可以将一棵完全二叉树以按层遍历的次序存储在数组中(这符合原则4)。我们把根祖宗放入数组索引 1 的位置,其他结点依次放入。为什么不放在索引 0 呢?因为除了根结点外,每个结点都有父节点。为了避免特殊情况,我们保留位置 0 为哑结点,使其可以当作根结点的父亲。此外,还有其他好处,不再一一列举。这样,我们对数组中任意索引 i 的结点,均可以在索引 2i 处找到它的左儿子。如果该位置超出了树中结点数,那我们就知道它没有左儿子。同理,它的右儿子在索引 2i+1 处。当然,我们也要测试其是否存在。它老子则在 i/2 索引处。
如果只需要插入,删除和找最小值三种操作,那么我们应该毫不犹豫的使用堆。那什么时候会有这种情况?比方说,喜欢我的MM有一个加强排。这么多人每天都围在你身边嗡嗡来嗡嗡去,咋应付啊?于是,我定个标准:每次,我都只找队伍里面最清纯的MM。这下,整个世界清净了。以后,当遇见新美女时,就把她放到队伍合适的位置。那些跟咱Say 88的MM,则一概从队伍里面开除。这个时候,这个队伍用堆来排列最合适不过。这听起来好像优先级队列啊。没错,堆还有一个别名,正是优先级队列。
很遗憾,.NET并没有提供优先级队列集合。我们只能自己编写,下面是完整源代码。
1
 using System;
using System;2
 using System.Collections.Generic;
using System.Collections.Generic;3

4
 namespace Lucifer.DataStructure
namespace Lucifer.DataStructure5
 {
{6
 public class PriorityQueue<T>
public class PriorityQueue<T>7
 {
{8
 #region 私有变量
#region 私有变量9

10
 private int theSize;
private int theSize;11
 private T[] theArray;
private T[] theArray;12
 private IComparer<T> theComparer;
private IComparer<T> theComparer;13

14
 private const int defaultCapacity = 100;
private const int defaultCapacity = 100;15

16
 #endregion
#endregion17

18
 #region 构造函数
#region 构造函数19

20
 public PriorityQueue()
public PriorityQueue()21
 : this(Comparer<T>.Default)
: this(Comparer<T>.Default)22
 {
{23
 }
}24

25
 public PriorityQueue(IComparer<T> comparer)
public PriorityQueue(IComparer<T> comparer)26
 {
{27
 this.theArray = new T[defaultCapacity];
this.theArray = new T[defaultCapacity];28
 this.theComparer = comparer;
this.theComparer = comparer;29
 }
}30

31
 public PriorityQueue(IEnumerable<T> collection)
public PriorityQueue(IEnumerable<T> collection)32
 {
{33
 this.theComparer = Comparer<T>.Default;
this.theComparer = Comparer<T>.Default;34

35
 ICollection<T> currentCollection = collection as ICollection<T>;
ICollection<T> currentCollection = collection as ICollection<T>;36

37
 if (currentCollection != null)
if (currentCollection != null)38
 {
{39
 this.theSize = currentCollection.Count;
this.theSize = currentCollection.Count;40
 this.theArray = new T[(theSize + 2) * 11 / 10];
this.theArray = new T[(theSize + 2) * 11 / 10];41
 currentCollection.CopyTo(theArray, 1);
currentCollection.CopyTo(theArray, 1);42
 }
}43
 else
else44
 {
{45
 int i = 1;
int i = 1;46
 foreach (T item in collection)
foreach (T item in collection)47
 {
{48
 this.theArray[i++] = item;
this.theArray[i++] = item;49
 theSize++;
theSize++;50
 }
}51
 }
}52

53
 this.BuildHeap();
this.BuildHeap();54
 }
}55

56
 #endregion
#endregion57

58
 #region 公有方法
#region 公有方法59
 /// <summary>
/// <summary>60
 /// 添加 item 到优先级队列中。
/// 添加 item 到优先级队列中。61
 /// </summary>
/// </summary>62
 /// <param name="item">要添加的值。</param>
/// <param name="item">要添加的值。</param>63
 public void Add(T item)
public void Add(T item)64
 {
{65
 if (theSize + 1 == theArray.Length)
if (theSize + 1 == theArray.Length)66
 {
{67
 Array.Resize<T>(ref theArray, theArray.Length == 0 ? defaultCapacity : (theArray.Length * 2));
Array.Resize<T>(ref theArray, theArray.Length == 0 ? defaultCapacity : (theArray.Length * 2));68
 }
}69
 /*
/*70
 * 向上过滤。
* 向上过滤。71
 */
*/72
 int hole = ++theSize;
int hole = ++theSize;73
 theArray[0] = item;
theArray[0] = item;74
 for (; theComparer.Compare(item, theArray[hole / 2]) < 0; hole /= 2)
for (; theComparer.Compare(item, theArray[hole / 2]) < 0; hole /= 2)75
 {
{76
 theArray[hole] = theArray[hole / 2];
theArray[hole] = theArray[hole / 2];77
 }
}78
 theArray[hole] = item;
theArray[hole] = item;79
 }
}80

81
 /// <summary>
/// <summary>82
 /// 清空优先级队列。
/// 清空优先级队列。83
 /// </summary>
/// </summary>84
 public void Clear()
public void Clear()85
 {
{86
 Array.Clear(theArray, 0, theSize);
Array.Clear(theArray, 0, theSize);87
 this.theSize = 0;
this.theSize = 0;88
 }
}89

90
 /// <summary>
/// <summary>91
 /// 移除优先级队列中最小项。
/// 移除优先级队列中最小项。92
 /// </summary>
/// </summary>93
 /// <returns>返回优先级队列中被移除的最小项。</returns>
/// <returns>返回优先级队列中被移除的最小项。</returns>94
 public T Remove()
public T Remove()95
 {
{96
 T item = this.GetMin();
T item = this.GetMin();97
 theArray[1] = theArray[theSize--];
theArray[1] = theArray[theSize--];98
 this.PercolateDown(1);
this.PercolateDown(1);99

100
 return item;
return item;101
 }
}102

103
 /// <summary>
/// <summary>104
 /// 获得优先级队列中最小项。
/// 获得优先级队列中最小项。105
 /// </summary>
/// </summary>106
 /// <returns>返回优先级队列中最小项。</returns>
/// <returns>返回优先级队列中最小项。</returns>107
 /// <exception>抛出 InvalidOperationException 异常,当队列为空时。</exception>
/// <exception>抛出 InvalidOperationException 异常,当队列为空时。</exception>108
 public T GetMin()
public T GetMin()109
 {
{110
 if (this.IsEmpty())
if (this.IsEmpty())111
 {
{112
 throw new InvalidOperationException("The queue is empty.");
throw new InvalidOperationException("The queue is empty.");113
 }
}114

115
 return theArray[1];
return theArray[1];116
 }
}117

118
 /// <summary>
/// <summary>119
 /// 判断优先级队列是否为空。
/// 判断优先级队列是否为空。120
 /// </summary>
/// </summary>121
 /// <returns>如果是空队列,返回 true 。否则,返回 false 。</returns>
/// <returns>如果是空队列,返回 true 。否则,返回 false 。</returns>122
 public bool IsEmpty()
public bool IsEmpty()123
 {
{124
 return theSize == 0;
return theSize == 0;125
 }
}126

127
 #endregion
#endregion128

129
 #region 公有属性
#region 公有属性130

131
 /// <summary>
/// <summary>132
 /// 获得优先级队列中项的数量。
/// 获得优先级队列中项的数量。133
 /// </summary>
/// </summary>134
 public int Count
public int Count135
 {
{136
 get
get137
 {
{138
 return theSize;
return theSize;139
 }
}140
 }
}141

142
 #endregion
#endregion143

144
 #region 私有方法
#region 私有方法145
 /*
/*146
 * 构造一个堆。
* 构造一个堆。147
 */
*/148
 private void BuildHeap()
private void BuildHeap()149
 {
{150
 for (int i = theSize / 2; i > 0; i--)
for (int i = theSize / 2; i > 0; i--)151
 {
{152
 this.PercolateDown(i);
this.PercolateDown(i);153
 }
}154
 }
}155

156
 /*
/*157
 * 向下过滤。
* 向下过滤。158
 */
*/159
 private void PercolateDown(int hole)
private void PercolateDown(int hole)160
 {
{161
 int child;
int child;162
 T item = theArray[hole];
T item = theArray[hole];163
 for (; hole * 2 <= theSize; hole = child)
for (; hole * 2 <= theSize; hole = child)164
 {
{165
 child = hole * 2;
child = hole * 2;166
 /*
/*167
 * 父结点并不总是有两个子结点。
* 父结点并不总是有两个子结点。168
 */
*/169
 if (child != theSize && theComparer.Compare(theArray[child + 1], theArray[child]) < 0)
if (child != theSize && theComparer.Compare(theArray[child + 1], theArray[child]) < 0)170
 {
{171
 child++;
child++;172
 }
}173

174
 if (theComparer.Compare(theArray[child], item) < 0)
if (theComparer.Compare(theArray[child], item) < 0)175
 theArray[hole] = theArray[child];
theArray[hole] = theArray[child];176
 else
else177
 break;
break;178
 }
}179
 theArray[hole] = item;
theArray[hole] = item;180
 }
}181

182
 #endregion
#endregion183
 }
}184
 }
}此外,还有一些别的堆。比如斜堆,偶堆,斐波那契堆等,不再阐述。有兴趣的朋友可以参考其他资料。
谨以此记录成长的脚步,同时和大家一起分享快乐。



 浙公网安备 33010602011771号
浙公网安备 33010602011771号