剑指offer刷题(Tree)
JZ26. 树的子结构
输入两棵二叉树A和B,判断B是不是A的子结构。(约定空树不是任意一个树的子结构)
B是A的子结构, 即 A中有出现和B相同的结构和节点值。
例如:
给定的树 A:
3
/ \
4 5
/ \
1 2
给定的树 B:
4
/
1
返回 true,因为 B 与 A 的一个子树拥有相同的结构和节点值。
限制:
0 <= 节点个数 <= 10000
题解
- 涉及树的问题,大部分用递归可以解决。
思路:
- 先判断A和B是否为空,有一个为空,就返回false;
- 以下三者满足一个即可返回true;
- 把A和B传入hasSubTree进行判断;
- 验证B是不是A的左子树;
- 验证B是不是A的右子树;
class Solution {
public boolean isSubStructure(TreeNode A, TreeNode B) {
if (A == null || B == null) return false;
// 我们规定树的子结构必须是 B 树的结构和结点值完全与 A 相同
// 如果B树和A树相同, 那么也是一种子结构
// 我们可以分为三种情况判断
// 1. A树与B树完全相等
// 2. A的左子树与B树完全相等
// 3. A的右子树与B树完全相等
// 此时可以分为三个递归遍历, 因为 || 具有短路性质, 如果在某一步返回 true, 则后面的递归不用执行直接返回
return hasSubTree(A, B) || isSubStructure(A.left, B) || isSubStructure(A.right, B);
}
public boolean hasSubTree(TreeNode A, TreeNode B) {
// 这里如果B为空,说明B已经访问完了,确定是A的子结构
if (B == null) return true;
//如果B不为空A为空,或者这两个节点值不同,说明B树不是A的子结构,直接返回false
if (A == null || A.val != B.val) return false;
//当前节点比较完之后还要继续判断左右子节点
return hasSubTree(A.left, B.left) && hasSubTree(A.right, B.right);
}
}
- 时间复杂度 O(MN) : 其中 M,N 分别为树 A 和 树 B 的节点数量;先序遍历树 A 占用 O(M) ,每次调用 recur(A, B) 判断占用 O(N) 。
- 空间复杂度 O(M) : 当树 A 和树 B 都退化为链表时,递归调用深度最大。当 M \leq NM≤N 时,遍历树 A 与递归判断的总递归深度为 M ;当 M>N 时,最差情况为遍历至树 A 叶子节点,此时总递归深度为 M。
二叉树的镜像
题目描述
操作给定的二叉树,将其变换为源二叉树的镜像。
输入描述:
二叉树的镜像定义:源二叉树
8
/ \
6 10
/ \ / \
5 7 9 11
镜像二叉树
8
/ \
10 6
/ \ / \
11 9 7 5
递归
我们在做二叉树题目时候,第一想到的应该是用递归来解决。
仔细看下题目的输入和输出,输出的左右子树的位置跟输入正好是相反的,于是我们可以递归的交换左右子树来完成这道题。
看一下动画就明白了:
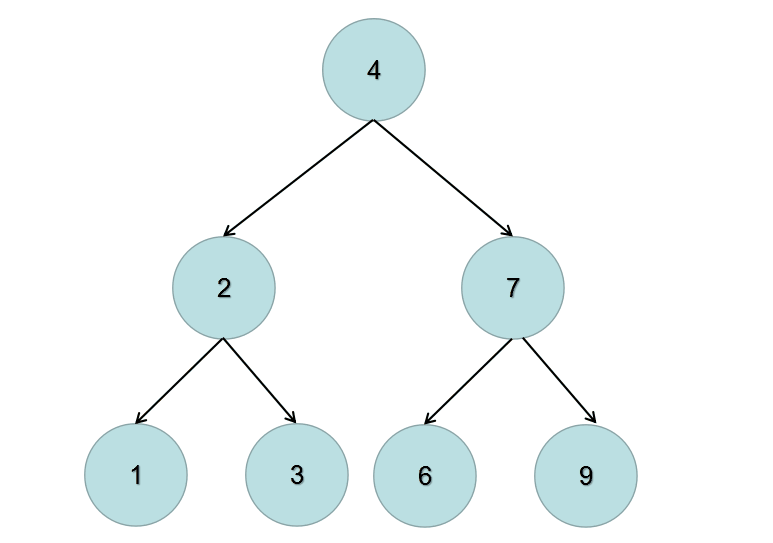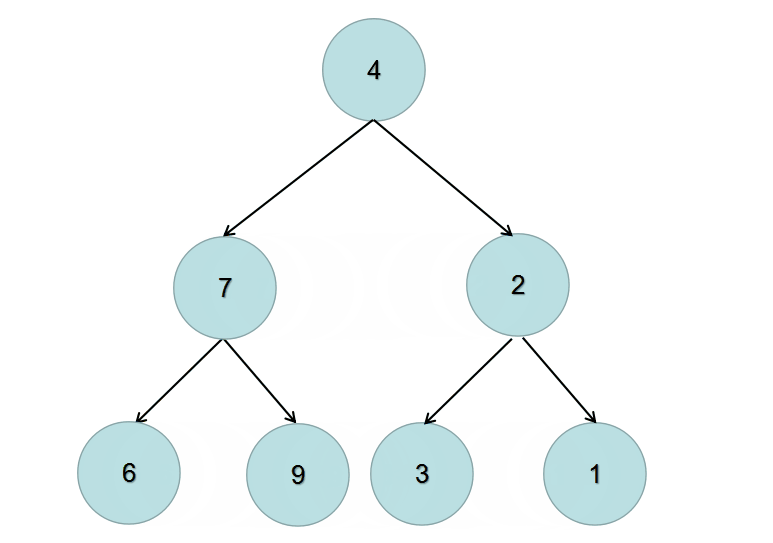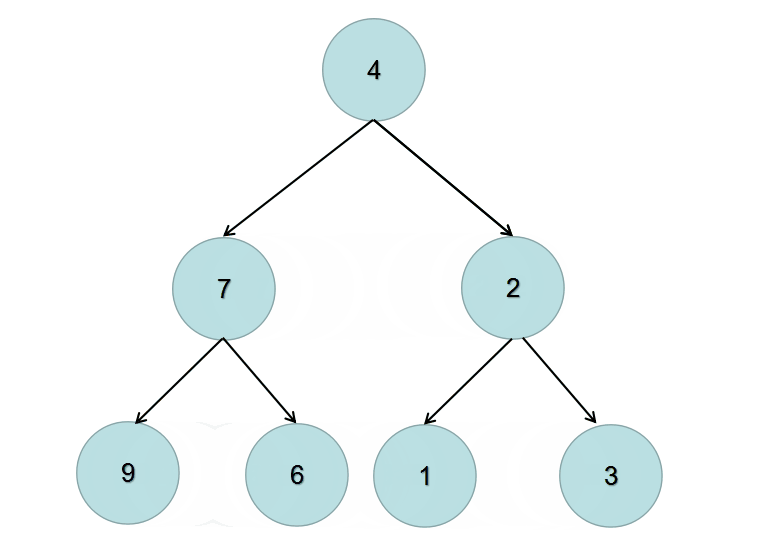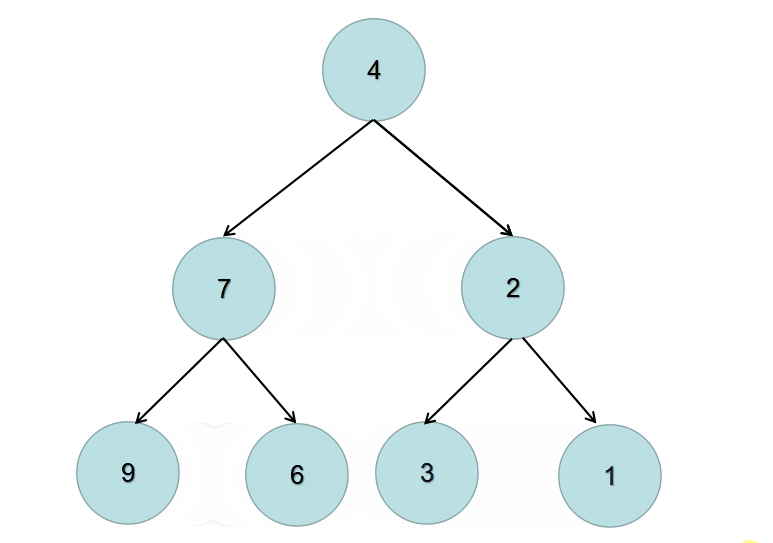
递归解析:
-
终止条件: 当节点 root 为空时(即越过叶节点),则返回 null ;
-
递推工作:
初始化节点 tmptmp ,用于暂存 root 的左子节点;
开启递归 右子节点 mirrorTree(root.right),并将返回值作为root 的 左子节点 。
开启递归 左子节点 mirrorTree(tmp),并将返回值作为 root 的 右子节点 。 -
返回值: 返回当前节点 root ;
- 时间复杂度:每个元素都必须访问一次,所以是O(N)
- 空间复杂度:最坏的情况下,需要存放O(h)个函数调用(h是树的高度),所以是O(h)
代码实现如下:
递归解法
class Solution {
public TreeNode mirrorTree(TreeNode root) {
//递归函数的终止条件,节点为空时返回
if(root==null) {
return null;
}
//下面三句是将当前节点的左右子树交换
TreeNode tmp = root.right;
root.right = root.left;
root.left = tmp;
//递归交换当前节点的 左子树
mirrorTree(root.left);
//递归交换当前节点的 右子树
mirrorTree(root.right);
//函数返回时就表示当前这个节点,以及它的左右子树
//都已经交换完了
return root;
}
}
迭代
递归实现也就是深度优先遍历的方式,那么对应的就是广度优先遍历。
广度优先遍历需要额外的数据结构--队列,来存放临时遍历到的元素。
深度优先遍历的特点是一竿子插到底,不行了再退回来继续;而广度优先遍历的特点是层层扫荡。
所以,我们需要先将根节点放入到队列中,然后不断的迭代队列中的元素。
对当前元素调换其左右子树的位置,然后:
- 判断其左子树是否为空,不为空就放入队列中
- 判断其右子树是否为空,不为空就放入队列中
动态图如下:
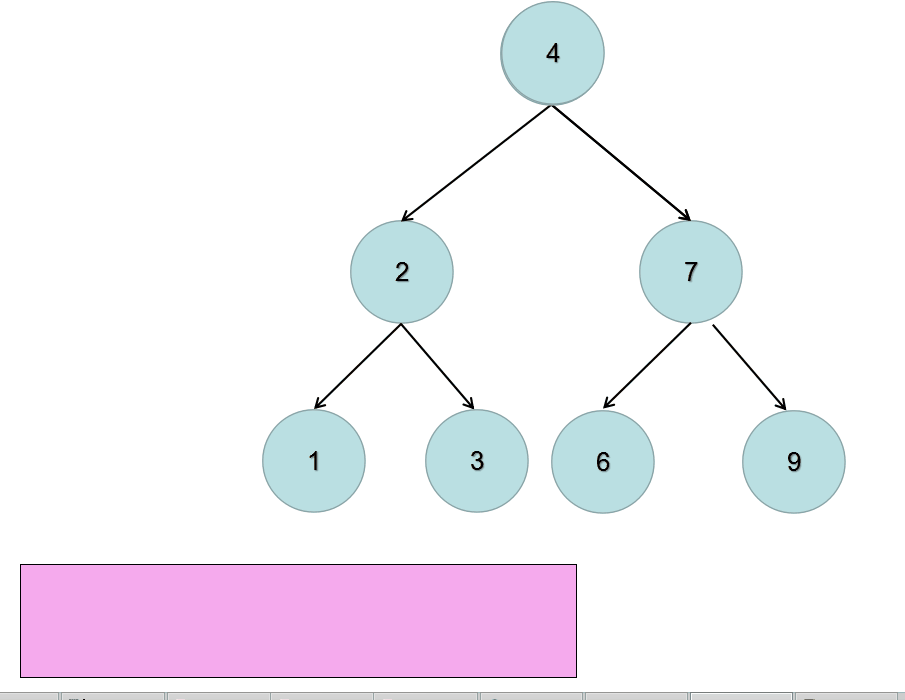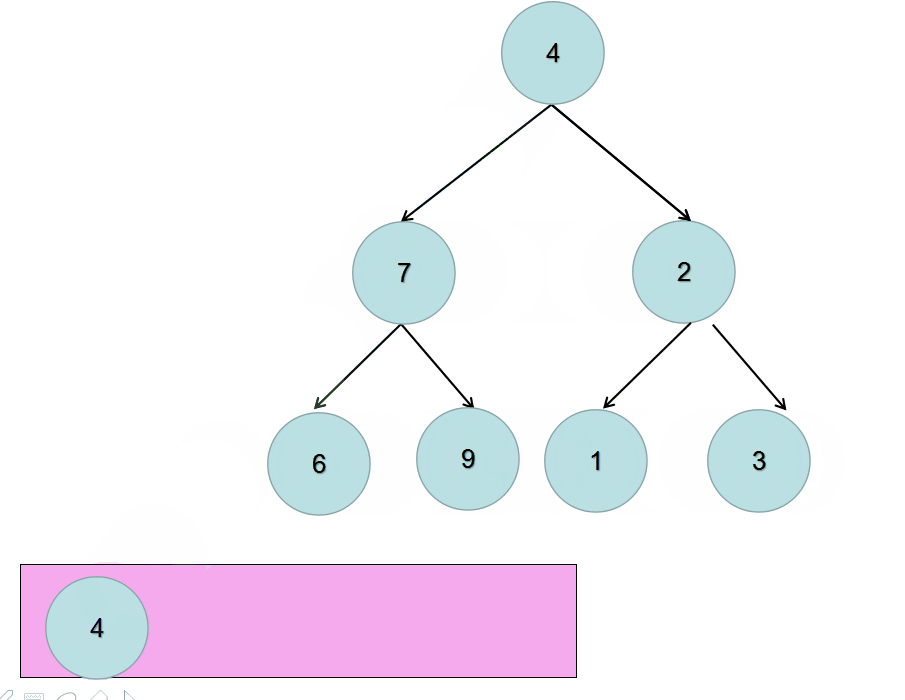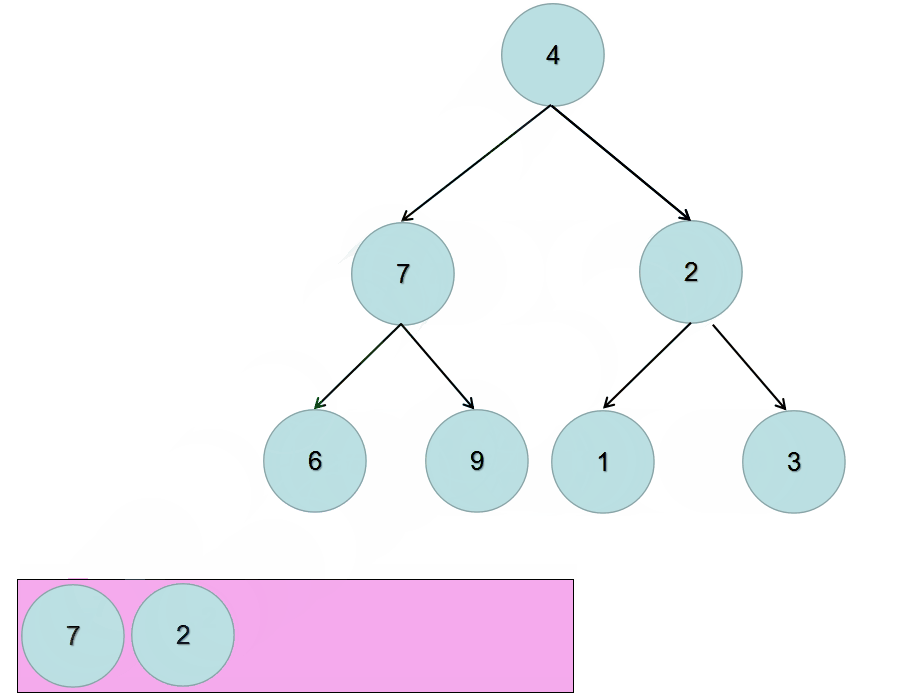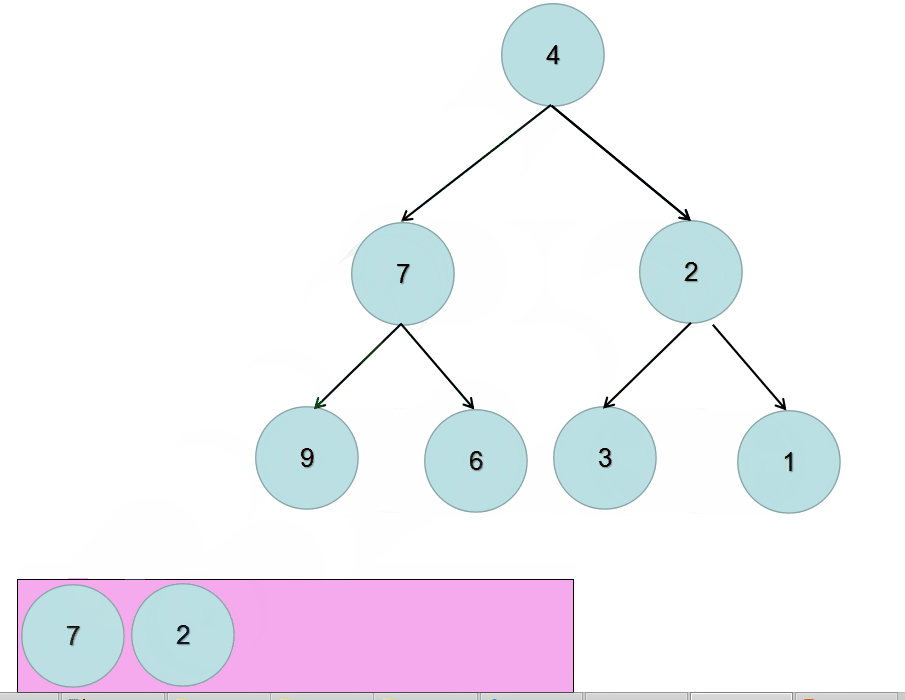
代码实现:
class Solution {
public TreeNode mirrorTree(TreeNode root) {
if(root==null) return null;
//将二叉树中的节点逐层放入队列中,再迭代处理队列中的元素
LinkedList<TreeNode> queue = new LinkedList<TreeNode>();
queue.add(root);
while(!queue.isEmpty()) {
//每次都从队列中拿一个节点,并交换这个节点的左右子树
TreeNode tmp = queue.poll();
TreeNode left = tmp.left;
tmp.left = tmp.right;
tmp.right = left;
//如果当前节点的左子树不为空,则放入队列等待后续处理
if(tmp.left!=null) {
queue.add(tmp.left);
}
//如果当前节点的右子树不为空,则放入队列等待后续处理
if(tmp.right!=null) {
queue.add(tmp.right);
}
}
//返回处理完的根节点
return root;
}
}
二叉树的层序遍历
题目描述
从上往下打印出二叉树的每个节点,同层节点从左至右打印。
示例1
输入
返回值
[5,4,3,2,1]
方法:层次遍历
这道题就是一个模板题,对队列的使用。因为要满足先进先出的特性。
- 初始化:一个队列queue<TreeNode*> q, 将root节点入队列q
- 如果队列不空,做如下操作:
- 弹出队列头,保存为node,将node的左右非空孩子加入队列
- 做2,3步骤,知道队列为空
代码:
public class Solution {
public ArrayList<Integer> PrintFromTopToBottom(TreeNode root) {
ArrayList<Integer> res = new ArrayList<>();
LinkedList<TreeNode> list = new LinkedList<>();
if(root == null) return res;
list.add(root);
while(!list.isEmpty()){
TreeNode temp = list.poll();
res.add(temp.val);
if(temp.left != null) list.add(temp.left);
if(temp.right != null) list.add(temp.right);
}
return res;
}
}
二叉树的最大深度
题目描述
输入一棵二叉树,求该树的深度。从根结点到叶结点依次经过的结点(含根、叶结点)形成树的一条路径,最长路径的长度为树的深度。
题解:递归法
public class Solution {
public int TreeDepth(TreeNode root) {
if(root == null) return 0;
return Math.max(TreeDepth(root.left) , TreeDepth(root.right)) + 1;
}
}
剑指 Offer 54. 二叉搜索树的第k大节点
给定一棵二叉搜索树,请找出其中第k大的节点。
示例 1:
输入: root = [3,1,4,null,2], k = 1
3
/ \
1 4
\
2
输出: 4
示例 2:
输入: root = [5,3,6,2,4,null,null,1], k = 3
5
/ \
3 6
/ \
2 4
/
1
输出: 4
限制:1 ≤ k ≤ 二叉搜索树元素个数
题解:
搜索二叉树的中序遍历结果就是按顺序排列的。
方法一:
- 1 中序遍历二叉树,遍历的结果放到数组list中;
- 2 第k大的数就是 list.size() - 1;
方法二:
- 当遍历到了第K大数的时候,就可以停止遍历了,同时,把遍历到节点对应的数保存下来即可。
代码:
//法一:
class Solution {
public int kthLargest(TreeNode root, int k) {
// clarification: root == null? k <= 1?
List<Integer> list = new ArrayList<>();
helper(root, list);
return list.get(list.size() - k);
}
private void helper(TreeNode root, List<Integer> list) {
if (root == null) return;
if (root.left != null) helper(root.left, list);
list.add(root.val);
if (root.right != null) helper(root.right, list);
}
}
//法二:
class Solution {
private int ans = 0, count = 0;
public int kthLargest(TreeNode root, int k) {
// clarification: root == null? k <= 1?
helper(root, k);
return ans;
}
private void helper(TreeNode root, int k) {
if (root.right != null) helper(root.right, k);
if (++count == k) {
ans = root.val;
return;
}
if (root.left != null) helper(root.left, k);
}
}
剑指 Offer 28. 对称的二叉树
请实现一个函数,用来判断一棵二叉树是不是对称的。如果一棵二叉树和它的镜像一样,那么它是对称的。
例如,二叉树 [1,2,2,3,4,4,3] 是对称的
1
/ \
2 2
/ \ / \
3 4 4 3
但是下面这个 [1,2,2,null,3,null,3] 则不是镜像对称的:
1
/ \
2 2
\ \
3 3
示例 1:
输入:root = [1,2,2,3,4,4,3]
输出:true
示例 2:
输入:root = [1,2,2,null,3,null,3]
输出:false
限制:
0 <= 节点个数 <= 1000
class Solution {
public boolean isSymmetric(TreeNode root) {
if(root == null) return true;
recur(root.left, root.right);
}
boolean recur(TreeNode L, TreeNode R) {
if(L == null && R == null) return true;
if(L == null || R == null || L.val != R.val) return false;
return recur(L.left, R.right) && recur(L.right, R.left);
}


 浙公网安备 33010602011771号
浙公网安备 33010602011771号