Monte Carlo：
通过极限情况下的分布关系$\pi (x’) =\sum\limits_{x}{ \pi (x)P(x->x’)} $
有p(x’)$\approx\sum\limits_{x}{p(x)T(x—>x’)}$
若T满足regular markov chain的条件，则Monte Carlo方法保证在极限条件下收敛到目标分布。
Regular Markov Chain
转移矩阵经过若干次相乘后，所有项都不为0的马尔科夫链就是规则马尔科夫链。
充分条件：任意两个状态都相连，每个状态自转移概率不为0.
An square matrix 
is called regular if for some integer 
all entries of 
are positive.
Example
The matrix
![\begin{displaymath}A = \left[ \begin{array}{rr}
0&1\\
1&0\\
\end{array}
\right]\end{displaymath}](https://www.math.ucdavis.edu/~daddel/linear_algebra_appl/Applications/MarkovChain/MarkovChain_9_18/img28.gif){kind=small}
is not a regular matrix, because for all positive integer ,
![\begin{displaymath}A^{2n} = \left[ \begin{array}{rr}
1&0\\
0&1\\
\end{arra...
...\left[ \begin{array}{rr}
0&1\\
1&0\\
\end{array}
\right]\end{displaymath}](https://www.math.ucdavis.edu/~daddel/linear_algebra_appl/Applications/MarkovChain/MarkovChain_9_18/img33.gif){kind=small}
The matrix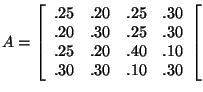 
is a regular matrix, because 
has all positive entries.
It can also be shown that all other eigenvalues of A are less than 1, and algebraic multiplicity of 1 is one.
It can be shown that if is a regular matrix then approaches to a matrix 
whose columns are all equal to a probability vector 
which is called the steady-state vector of the regular Markov chain.
![\begin{displaymath}\mbox{ if } A \mbox{ regular, then } A^n \rightarrow Q = \lef...
...&&.\\
.&.&&&&.\\
q_k&q_k&.&.&.&q_k\\
\end{array}
\right]\end{displaymath}](https://www.math.ucdavis.edu/~daddel/linear_algebra_appl/Applications/MarkovChain/MarkovChain_9_18/img38.gif)
where 
.
It can be shown that for any probability vector 
when gets large, 
approaches to the steady-state vector
![\begin{displaymath}{\bf q } = \left[ \begin{array}{r}
q_1\\
q_2\\
\vdots \\
q_k\\
\end{array}
\right]\end{displaymath}](https://www.math.ucdavis.edu/~daddel/linear_algebra_appl/Applications/MarkovChain/MarkovChain_9_18/img41.gif)
.
That is
![\begin{displaymath}A^n x^{(0)} \longrightarrow q=\left[ \begin{array}{r}
q_1\\
q_2\\
.\\
.\\
.\\
q_k\\
\end{array}
\right]\end{displaymath}](https://www.math.ucdavis.edu/~daddel/linear_algebra_appl/Applications/MarkovChain/MarkovChain_9_18/img42.gif)
where .
It can also be shown that the steady-state vector q is the only vector such that
Note that this shows q is an eigenvector of A and 
is eigenvalue of A.
Mixed：收敛的
验证方法，通常不能验证已经mixed，但是能验证还不是mixed：
1、使用windows，截取一个时间段的数据看是否相近。但是可能在收敛过程中有小部分数据先聚集到一起，这不能说明是收敛的。
2、使用两个不同的初始状态的马尔科夫链。在同一个时间观察，如果数据不相近，则不是mixed。
实际中可以使用一个随机初始的，和一个高概率初始的来比较。
MCMC方法取得的样本不是IID的，所以有时需要间隔一段再取。
The faster the Markov Chain converges, the less correlated are the samples.
Gibbs Sampling
对多维数据有效。
不能mix的gibbs sampling chain
metropolis-hastings
