绪论作业

---恢复内容开始---

一、作业题目

仿照三元组或复数的抽象数据类型写出有理数抽象数据类型的描述 （有理数是其分子、分母均为整数且分母不为零的分数）。

　　有理数基本运算：

1. 构造有理数T，元素e1,e2分别被赋以分子、分母值
2. 销毁有理数T
3. 用e(引用类型参数)返回有理数T的分子或分母,当入参i为1时返回分子, i为2是返回分母。
4. 将有理数T的分子或分母更改为e,入参i为1时改变分子, i为2是改变分母
5. 有理数T1,T2相加,结果存入有理数T3
6. 有理数T1,T2相减,结果存入有理数T3
7. 有理数T1,T2相乘,结果存入有理数T3
8. 有理数T1,T2相除,结果存入有理数T3

二、博客作业

1、作业内容

用ADT抽象数据模型描述我的有理数数据类型

ADT Rational{

        数据对象：D={x,y|x,y都属于整型}x,y存放于T这个结构数组中；

        数据关系：R={<x,y>|x是分子，y是分母}；

        基本操作：

                       CreateRational(&T,r1,r2) 操作结果：构造有理数T

                       DestroyRational(&T) 操作结果：销毁有理数T

                       Get(&T,i,&e) 操作结果：返回有理数e

                       Change(&T,i,e) 操作结果：改变有理数的值

                       Addition(&T1,&T2,&T3) 操作结果：有理数T1,T2相加

                       Subtract(&T1,&T2,&T3) 操作结果：有理数T1，T2相减

                       Multiple(&T1,&T2,&T3) 操作结果：有理数T1，T2相乘

                       Divide(&T1,&T2,&T3) 操作结果：有理数T1,T2相除

                    }ADT Rational

2、数据结构，函数说明

        1、头文件

  

    2、函数

3、函数实现说明

   （1）构造函数

 

  （2）销毁有理数

 （3）返回分子分母的值

 （4）改变分子分母的值

 （5）有理数相加

  （6）有理数相减

 （7）有理数相乘

 （8）有理数相除

（9）求最大公约数

4、运行结果

 （1）正常情况

（2）分子为负数

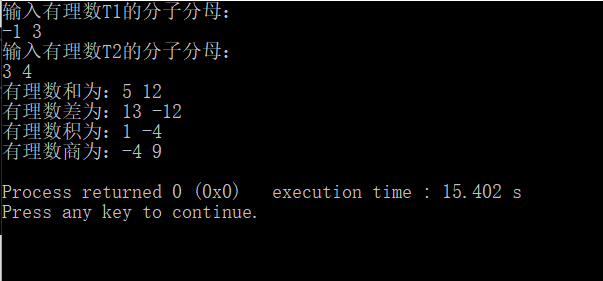
（3）和为整数

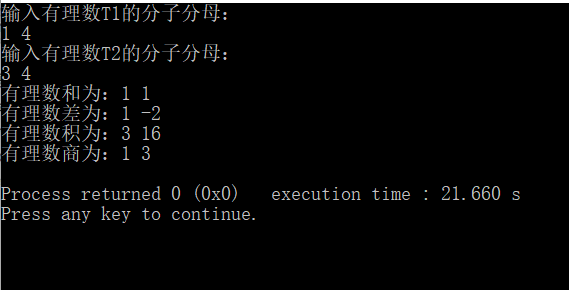
（4）分母为0

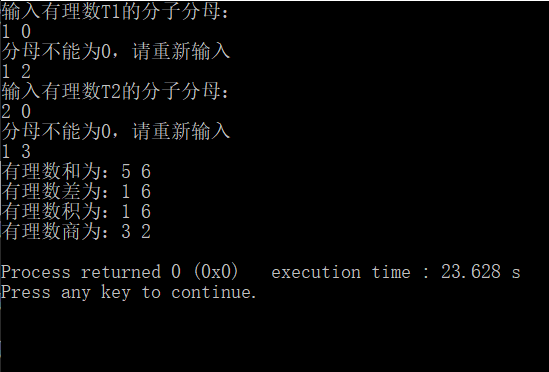
5、作业总结

本次作业让我学习到了很多东西，加深了我对数据结构的印象，刷新了我对数据结构的理解，在我看来，数据结构顾名思义就是数据的结构，就是数据之间的关系，将信息集合，提高算法的效率。让我们在开始编程之前会思考并构建好程序的结构，显得更有逻辑。而抽象数据类型则让我们能理清楚思路，更好的解决问题。

---恢复内容结束---