人工智能深度学习入门练习之（33）深度学习 – 自适应线性单元

深度学习 – 自适应线性单元

如前所述，在 20 世纪 50 年代，感知器 (Rosenblatt, 1956, 1958) 成为第一个能根据每个类别的输入样本来学习权重的模型。约在同一时期，自适应线性单元 (adaptive linearelement, ADALINE) 简单地返回函数 f(x) 本身的值来预测一个实数 (Widrow and Hoff, 1960)，并且它还可以学习从数据预测这些数。

自适应线性单元(Adaline)的激活函数是一个线性函数，该函数的输出等于输入，实际上就相当于没有激活函数，线性激活函数$\phi (Z)$的定义：

$\phi (Z)=Z=W^{T}X$

自适应线性单元的训练

自适应线性单元的训练规则

• 权重根据线性激活函数进行更新
• 将样本数据中的实际输出与线性激活函数的输出进行比较，计算模型偏差，然后更新权重。

感知器训练规则

• 权重是根据单位阶跃函数更新的
• 将样本数据中的实际输出与模型输出进行比较，计算模型偏差，然后更新权重。

自适应线性单元与感知器的区别，在与激活函数不同，自适应线性单元将返回一个实数值而不是0,1分类。因此自适应线性单元用来解决回归问题而不是分类问题。

自适应线性单元训练时，用于调节权重的训练算法是被称为随机梯度下降（stochastic gradient descent）的一种特例。稍加改进后的随机梯度下降算法仍然是当今深度学习的主要训练算法。后面将详细介绍。

监督学习与无监督学习

监督学习：对有标记（分类）的训练样本进行学习，以尽可能对训练样本集外的数据进行标记（分类）预测。

监督学习中，所有的标记（分类）是已知的。因此，训练样本的岐义性低。

无监督学习：对没有标记（分类）的训练样本进行学习，以发现训练样本集中的结构性知识。

这里，所有的标记（分类）是未知的。因此，训练样本的岐义性高。

聚类就是典型的无监督学习，经过聚类后的样本数据就可以用来做监督学习。

目标函数

通常，神经网络的训练都属于监督学习类别，即使样本数据没有分类，也可先做聚类处理，把样本数据分类，然后就可以用来做监督学习了。

在监督学习下，对于一个样本，我们知道它的特征（输入）$x$，以及标记（输出）$y$。同时，我们还可以得到神经网络的预测输出$\hat{y}$。注意这里面我们用$y$表示训练样本里面的标记，也就是实际值；用$\hat{y}$表示神经网络的的预测值。我们当然希望预测值$\hat{y}$和实际值$y$越接近越好。

数学上有很多方法来表示预测值$\hat{y}$和实际值$y$接近程度，比如我们可以用$\hat{y}$和$y$的差的平方的$\genfrac{}{}{0ex}{}{1}{2}$来表示它们的接近程度

 

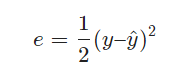
 我们把

$e$叫做单个样本的误差。至于为什么前面要乘$\genfrac{}{}{0ex}{}{1}{2}$，是为了后面计算方便。

训练数据中会有很多样本，比如$N$个，我们可以用训练数据中所有样本的误差的和，来表示神经网络的误差$E$，也就是

 

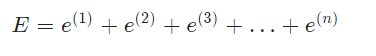
 上式的

$e^{(1)}$表示第一个样本的误差，$e^{(2)}$表示第二个样本的误差……。

上面的也可以表示为和式：

 

 x

${}^{(i)}$表示第$i$个训练样本的特征，$y^{(i)}$表示第$i$个样本的标记，我们也可以用元组$(x^{(i)},y^{(i)})$表示第$i$个训练样本。${\hat{y}}^{(i)}$则是神经网络对第$i$个样本的预测值，$\phi (z^{(i)})$中$z^{(i)}$表示第$i$个样本的加权求和值，$\phi (z)$表示线性激活函数。

对于一个训练数据集来说，我们当然希望误差$E$最小越好。对于特定的训练数据集来说，$(x^{(i)},y^{(i)})$的值都是已知的，所以$E$其实是参数$w$的函数。

 

 由此可见，神经网络的训练，实际上就是求取到合适的权重

$w$，使差值$E$取得最小值。这在数学上称作优化问题，而$J(w)$就是我们优化的目标，称之为目标函数，也被称为代价函数、损失函数。

注意：前面提到，目标函数实际上是差值平方和，从数学上来说，平方与线性激活函数让目标函数变成可微凸函数。
对于可微凸函数，可以使用一种简单但功能强大的优化算法，梯度下降法来求取目标函数$J(w)$的最小值，及其对应的参数$w$。

深度学习 – 梯度下降法

梯度下降法的主要思想是沿着损失函数的曲线下降，直到到达局部或全局的最小值点。

从数学上来看，梯度是指某点的切线斜率，即导数或偏导数（多元函数），在顶点斜率为0，所以找到斜率为0的点就是极值点。

梯度是函数值相对于自变量的变化率，变化率正负表示梯度方向，变化率为正，自变量变大函数值也变大，变化率为负，自变量变大函数值变小。为了找到函数极小值，自变量应该朝函数值变小的方向迈进，即梯度的反方向。

在每次迭代中，权重更新的步长与梯度方向相反，步长大小由学习率的值决定。

用梯度下降法求取损失函数最小值的步骤

 

 

损失函数的偏导数计算

在上面的内容中，我们直接给出了计算偏导数的公式，下面是该公式的推导过程。如不敢兴趣可跳过。

从上一章中，我们得知损失函数可以表示为：

 

 

梯度下降法的分类

批量梯度下降(Batch gradient descent)

上面使用的梯度下降法，每次都使用全量的训练集样本来更新模型参数，被称为批量梯度下降法。

批量梯度下降每次学习都使用整个训练集，因此其优点在于每次更新都会朝着正确的方向进行，最后能够保证收敛于极值点(凸函数收敛于全局极值点，非凸函数可能会收敛于局部极值点)，但是其缺点在于每次学习时间过长，并且如果训练集很大以至于需要消耗大量的内存，并且批量梯度下降不能进行在线模型参数更新。

随机梯度下降(Stochastic gradient descent)

随机梯度下降算法每次从训练集中随机选择一个样本来进行学习。

批量梯度下降算法每次都会使用全部训练样本，因此这些计算是冗余的，因为每次都使用完全相同的样本集。而随机梯度下降算法每次只随机选择一个样本来更新模型参数，因此每次的学习是非常快速的，并且可以进行在线更新。

随机梯度下降最大的缺点在于每次更新可能并不会按照正确的方向进行，因此可以带来优化波动(扰动)。

不过从另一个方面来看，随机梯度下降所带来的波动有个好处就是，对于类似盆地区域（即很多局部极小值点）那么这个波动的特点可能会使得优化的方向从当前的局部极小值点跳到另一个更好的局部极小值点，这样便可能对于非凸函数，最终收敛于一个较好的局部极值点，甚至全局极值点。

由于波动，因此会使得迭代次数（学习次数）增多，即收敛速度变慢。不过最终其会和全量梯度下降算法一样，具有相同的收敛性，即凸函数收敛于全局极值点，非凸损失函数收敛于局部极值点。

小批量梯度下降(Mini-batch gradient descent)

Mini-batch 梯度下降综合了 batch 梯度下降与 stochastic 梯度下降，在每次更新速度与更新次数中间取得一个平衡，其每次更新从训练集中随机选择 m, m < n 个样本进行学习。

相对于随机梯度下降，Mini-batch梯度下降降低了收敛波动性，即降低了参数更新的方差，使得更新更加稳定。相对于批量梯度下降，其提高了每次学习的速度。并且其不用担心内存瓶颈从而可以利用矩阵运算进行高效计算。一般而言每次更新随机选择[50,256]个样本进行学习，但是也要根据具体问题而选择，实践中可以进行多次试验，选择一个更新速度与更次次数都较适合的样本数。

深度学习 – 学习率

超参数

超参数是开发人员在构建模型时根据经验预先设置的参数，例如，网络层数，每层的神经元数量。

超参数不包括训练中学习的参数，例如，权重与偏置。

感知器和Adaline算法的超参数为:

• 学习率$\eta$
• epoch次数

学习率表示学习的速度，影响训练过程中，权重每次调整的值大小。

epoch是指一个完整的训练，即训练集中的数据都跑过一遍。

学习率选择

实践中，通常需要做一些实验，找到一个最适合的学习率$\eta$，可以让训练过程达到最优收敛。

学习率过小，导致收敛速度慢，步子小速度慢；学习率过大，导致找不到最小值点，步子太大跨过去了。

左边的图展示了最优学习率，成本函数可以快速收敛到全局最小值，但是如果学习率太小，收敛过程会变得很慢。

右边的图展示了，当选了一个很大的学习率，在调整权重时，有可能会跳过全局最小值。

 

 

如前所述，在 20 世纪 50 年代，感知器 (Rosenblatt, 1956, 1958) 成为第一个能根据每个类别的输入样本来学习权重的模型。约在同一时期，自适应线性单元 (adaptive linearelement, ADALINE) 简单地返回函数 f(x) 本身的值来预测一个实数 (Widrow and Hoff, 1960)，并且它还可以学习从数据预测这些数。

自适应线性单元(Adaline)的激活函数是一个线性函数，该函数的输出等于输入，实际上就相当于没有激活函数，线性激活函数$\phi (Z)$的定义：

$\phi (Z)=Z=W^{T}X$

自适应线性单元的训练

自适应线性单元的训练规则

• 权重根据线性激活函数进行更新
• 将样本数据中的实际输出与线性激活函数的输出进行比较，计算模型偏差，然后更新权重。

感知器训练规则

• 权重是根据单位阶跃函数更新的
• 将样本数据中的实际输出与模型输出进行比较，计算模型偏差，然后更新权重。

自适应线性单元与感知器的区别，在与激活函数不同，自适应线性单元将返回一个实数值而不是0,1分类。因此自适应线性单元用来解决回归问题而不是分类问题。

自适应线性单元训练时，用于调节权重的训练算法是被称为随机梯度下降（stochastic gradient descent）的一种特例。稍加改进后的随机梯度下降算法仍然是当今深度学习的主要训练算法。后面将详细介绍。

监督学习与无监督学习

监督学习：对有标记（分类）的训练样本进行学习，以尽可能对训练样本集外的数据进行标记（分类）预测。

监督学习中，所有的标记（分类）是已知的。因此，训练样本的岐义性低。

无监督学习：对没有标记（分类）的训练样本进行学习，以发现训练样本集中的结构性知识。

这里，所有的标记（分类）是未知的。因此，训练样本的岐义性高。

聚类就是典型的无监督学习，经过聚类后的样本数据就可以用来做监督学习。

目标函数

通常，神经网络的训练都属于监督学习类别，即使样本数据没有分类，也可先做聚类处理，把样本数据分类，然后就可以用来做监督学习了。

在监督学习下，对于一个样本，我们知道它的特征（输入）$x$，以及标记（输出）$y$。同时，我们还可以得到神经网络的预测输出$\hat{y}$。注意这里面我们用$y$表示训练样本里面的标记，也就是实际值；用$\hat{y}$表示神经网络的的预测值。我们当然希望预测值$\hat{y}$和实际值$y$越接近越好。

数学上有很多方法来表示预测值$\hat{y}$和实际值$y$接近程度，比如我们可以用$\hat{y}$和$y$的差的平方的$\genfrac{}{}{0ex}{}{1}{2}$来表示它们的接近程度

$e=\genfrac{}{}{0ex}{}{1}{2}(y–^{)}^2$

我们把$e$叫做单个样本的误差。至于为什么前面要乘$\genfrac{}{}{0ex}{}{1}{2}$，是为了后面计算方便。

训练数据中会有很多样本，比如$N$个，我们可以用训练数据中所有样本的误差的和，来表示神经网络的误差$E$，也就是

$E=e^{(1)}+e^{(2)}+e^{(3)}+\dots +e^{(n)}$

上式的$e^{(1)}$表示第一个样本的误差，$e^{(2)}$表示第二个样本的误差……。

上面的也可以表示为和式：

$\begin{array}{rl}E& =e^{(1)}+e^{(2)}+e^{(3)}+\dots +e^{(n)}\\ & =\stackrel{n\sum }{i=1}{e}^{(i)}\\ & =\genfrac{}{}{0ex}{}{1}{2}\stackrel{n\sum }{i=1}(y^{(i)}–{\hat{y}}^{(i)}{)}^2\end{array}$

其中

${\hat{y}}^{(i)}=\phi (z^{(i)})=w^T{x}^{(i)}$

$x^{(i)}$表示第$i$个训练样本的特征，$y^{(i)}$表示第$i$个样本的标记，我们也可以用元组$(x^{(i)},y^{(i)})$表示第$i$个训练样本。${\hat{y}}^{(i)}$则是神经网络对第$i$个样本的预测值，$\phi (z^{(i)})$中$z^{(i)}$表示第$i$个样本的加权求和值，$\phi (z)$表示线性激活函数。

对于一个训练数据集来说，我们当然希望误差$E$最小越好。对于特定的训练数据集来说，$(x^{(i)},y^{(i)})$的值都是已知的，所以$E$其实是参数$w$的函数。

$\begin{array}{rl}E=J(w)& =\genfrac{}{}{0ex}{}{1}{2}\stackrel{n\sum }{i=1}(y^{(i)}–{\hat{y}}^{(i)}{)}^2\\ & =\genfrac{}{}{0ex}{}{1}{2}\stackrel{n\sum }{i=1}(y^{(i)}–\phi (z^{(i)}){)}^2\\ & =\genfrac{}{}{0ex}{}{1}{2}\stackrel{n\sum }{i=1}(y^{(i)}–w^T{x}^{(i)}{)}^2\end{array}$

由此可见，神经网络的训练，实际上就是求取到合适的权重$w$，使差值$E$取得最小值。这在数学上称作优化问题，而$J(w)$就是我们优化的目标，称之为目标函数，也被称为代价函数、损失函数。

注意：前面提到，目标函数实际上是差值平方和，从数学上来说，平方与线性激活函数让目标函数变成可微凸函数。
对于可微凸函数，可以使用一种简单但功能强大的优化算法，梯度下降法来求取目标函数$J(w)$的最小值，及其对应的参数$w$。

---

Doc navigation

 

深度学习 - 梯度下降法 →

 

---

浙ICP备17015664号 浙公网安备 33011002012336号 联系我们 网站地图 站长统计  

@2019 qikegu.com 版权所有，禁止转载