8.23HL 周赛

\(100+100+100+30+100+0+0+0=430pts\)

AB跳了，签到

C

题目

首先很明显是个 $dp$

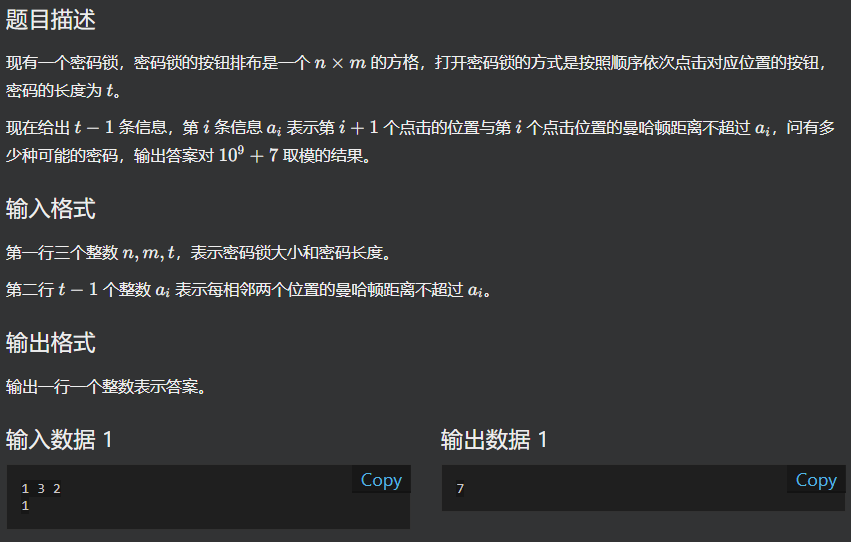
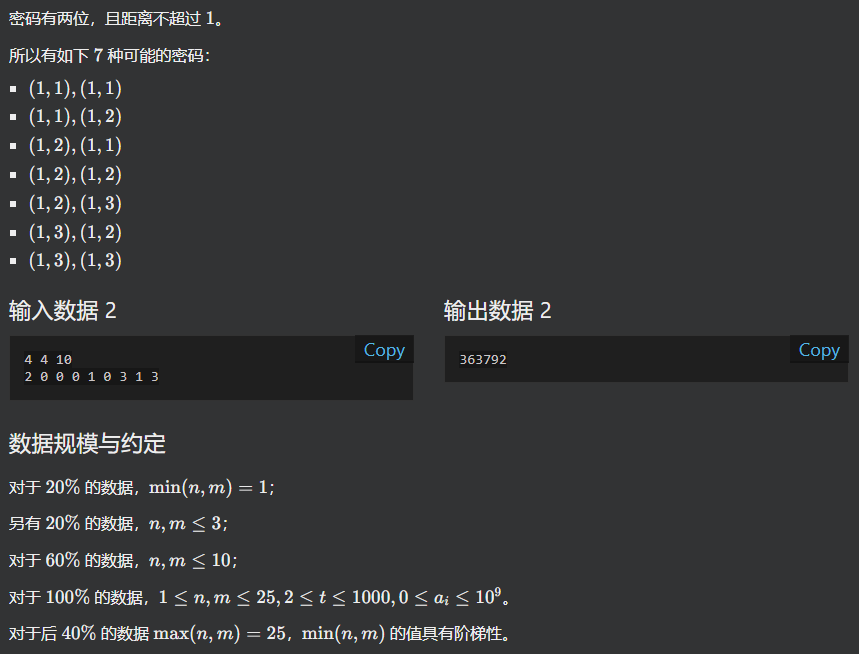
自从有一次模拟赛用过曼哈顿转切比雪夫后，就念念不忘了

然后尝试使用转切比雪夫变成正方形，再用二维差分做

当然会失败了，还浪费了半个小时

观察一下数据范围，发现 \(O(n^2mq)\) 也是可以过的

于是用前缀和优化掉一层循环，就完事了

CODE

#include<bits/stdc++.h>
#define abs(x) ((x)<0 ? (-(x)) : (x))
#define usetime() (double)clock () / CLOCKS_PER_SEC * 1000.0
using namespace std;
typedef long long LL;
const int maxn=28;
const int mod=1e9+7;
void read(int& x){
	char c;
	bool f=0;
	while((c=getchar())<48) f|=(c==45);
	x=c-48;
	while((c=getchar())>47) x=(x<<3)+(x<<1)+c-48;
	x=(f ? -x : x);
}
LL a[2][maxn][maxn];
int n,m,k;
int main(){
	read(n),read(m),read(k);
	for(int i=1;i<=n;i++){
		for(int j=1;j<=m;j++){
			a[0][i][j]=a[0][i][j-1]+1;
		}
	}
	int lim;
	for(int i=1;i<k;i++){
		read(lim);
		for(int x1=1;x1<=n;x1++){
			for(int y1=1;y1<=m;y1++){
				for(int x2=1;x2<=n;x2++){
					int l=lim-abs(x1-x2);
					if(l<0) continue;
					a[1][x1][y1]+=a[0][x2][min(y1+l,m)]-a[0][x2][max(y1-l-1,0)]+mod;
					a[1][x1][y1]%=mod;
				}
			}
		}
		for(int x=1;x<=n;x++){
			for(int y=1;y<=m;y++){
				a[0][x][y]=a[0][x][y-1]+a[1][x][y];
				a[1][x][y]=0;
			}
		}
	}
	LL ans=0;
	for(int x=1;x<=n;x++){
		for(int y=1;y<=m;y++){
			ans+=a[0][x][y]-a[0][x][y-1];
			ans%=mod;
		}
	}
	printf("%lld",ans);
	return 0;
}
//^o^

D

题目

公式题

特殊路径最多只会走一次

于是乎

\[|x2-x1|+min(n-|y1-y2|+1,|y1-y2|) \]

\[n-|x1-x2|+1+min(n-|n-y1-y2|+1,|n-y1-y2|)) \]

两者取较小值

CODE

#include<bits/stdc++.h>
#define abs(x) ((x)<0 ? (-(x)) : (x))
#define usetime() (double)clock () / CLOCKS_PER_SEC * 1000.0
using namespace std;
typedef long long LL;
void read(LL& x){
	char c;
	bool f=0;
	while((c=getchar())<48) f|=(c==45);
	x=c-48;
	while((c=getchar())>47) x=(x<<3)+(x<<1)+c-48;
	x=(f ? -x : x);
}
LL n,q;
signed main(){
	read(n),read(q);
	LL x1,y1,x2,y2;
	while(q--){
		read(x1),read(y1),read(x2),read(y2);
		LL ans=min(abs(x2-x1)+min(n-abs(y1-y2)+1,abs(y1-y2)),\
				   n-abs(x1-x2)+1+min(n-abs(n-y1-y2)+1,abs(n-y1-y2)));
		printf("%lld\n",ans);
	}
	return 0;
}
//^o^

E

题目

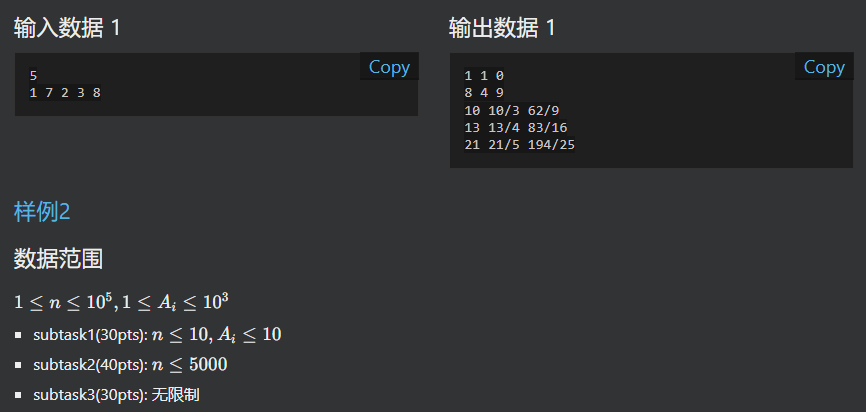
最劣解，思路不一样

好吧，时间不够了

不写了，放代码，就是求了个递推式，导致实现难度剧增

8.26补

我不想写数学公式了

就是每次平均数都会发生变化，相当于加上一个 \(k\)

然后把平方展开，发现增加的值会与项数和所有元素的和有关

式子自己推一下，详见代码

CODE

#include<bits/stdc++.h>
#define usetime() (double)clock () / CLOCKS_PER_SEC * 1000.0
#define abs(x) ((x)<0 ? (-(x)) : (x))
using namespace std;
typedef __int128 LL;
const int maxn=1e5+5;
void read(LL& x){
	char c;
	bool f=0;
	while((c=getchar())<48) f|=(c==45);
	x=c-48;
	while((c=getchar())>47) x=(x<<3)+(x<<1)+c-48;
	x=(f ? -x : x);
}
void write(LL x){
	if(x){
		write(x/10);
		printf("%d",(int)(x%10));
	}
}
struct num{
	LL m,s;
	num(LL si=0,LL mi=1){
		if(mi<0) si=-si,mi=-mi;
		m=mi,s=si;
		work();
	}
	void work(){
		if(m<0) s=-s,m=-m;
		LL temp=abs(__gcd(m,s));
		if(!temp) return;
		m/=temp,s/=temp;
	}
	num operator*(const LL& x)const{
		LL temp=__gcd(x,m);
		return num(x/temp*s,m/temp);
	}
	num operator/(const LL& x)const{
		LL temp=__gcd(x,s);
		return num(s/temp,x/temp*m);
	}
	num operator+(const LL& x)const{
		return num(s+x*m,m);
	}
	num operator-(const LL& x)const{
		return num(s-x*m,m);
	}
	num operator-(const num& x)const{
		LL temp=abs(__gcd(m,x.m));
		LL mi=x.m/temp*m;
		return num(s*mi/m-x.s*mi/x.m,mi);
	}
	num operator+(const num& x)const{
		LL temp=abs(__gcd(m,x.m));
		LL mi=x.m/temp*m;
		return num(mi/m*s+mi/x.m*x.s,mi);
	}
	num operator*(const num& x)const{
		int temp1=__gcd(x.s,m),temp2=__gcd(s,x.m);
		return num((s/temp2)*(x.s/temp1),(m/temp1)*(x.m/temp2));
	}
	num pow2(){
		return num(s*s,m*m);
	}
	void print(){
		if(m==1){
			write(s);
			if(!s) putchar('0');
		}
		else{
			write(s);
			if(!s) putchar('0');
			putchar('/');
			write(m);
			if(!m) putchar('0');
		}
	}
};
LL n;
LL a[maxn];
int main(){
	read(n);
	for(int i=1;i<=n;i++) read(a[i]);
	LL sum=0;
	num av,sq;
	for(int i=1;i<=n;i++){
		sum+=a[i];
		sq=sq+(av-a[i])*(av-a[i]);
		num tp=num(sum,i)-av;
		sq=sq+tp*2*(av*i-sum)+tp.pow2()*i;
		av=num(sum,i);
		if(i==1) sq=num();
		write(sum);
		if(!sum) putchar('0');
		putchar(' ');
		av.print(),putchar(' ');
		(sq/i).print(),putchar('\n');
	}
	return 0;
}
//^o^