梯度下降和反向传播算法推导
梯度下降算法的公式:
其中,是\(▽\)梯度算子,\(▽f(x)\)就是指\(f(x)\)的梯度。\(\eta\)是步长,也称作学习速率。用\(\bar{y}\)代表输入\(x\)对应的输出,为了表示X,Y的对应关系,我们定义了线性回归的方程:
有样本标签值\(y\),和基于当\(w\),\(b\)状态下的\(\bar{y}\),我们可以根据下面的公式计算LOSS。所以对于线性回归,Sum Squre Residual (SSE)公式如下:
\(E\)是所以预测样本的误差和,这个求和公式代表着我们要对所有样本点都计算误差在汇总为一个数值,均方误差为什么还除以2?
因为带了平方,后面要用梯度下降法,要求导,这样求导多出的乘2就和二分之一抵消了,一个简化后面计算的技巧
梯度下降算法可以写成:
另外梯度上升的公式就是:
同理b也是如此\(Bnew=Bold+\eta▽E\)
推导过程
\(▽E\)的推导:
我们计算导数的目的就是为了更新相对应的参数。简而言之,你需要更新哪个参数,就对哪个参数求导。
比如我们现在想要更新\(w\)参数:
提取出\(\sum\)里的:
\(y\)是与\(w\)无关的常数,而\(\bar{y}=wx\),所以根据链式求导得:
\(\frac{\partial E}{\partial \bar{y}}\)与\(\frac{\partial \bar{y}}{\partial w}\)分开求导:
所以:
然后如果我们再想更新偏置项\(b\):
提取出\(\sum\)里的:
\(\frac{\partial E}{\partial \bar{y}}\)与\(\frac{\partial \bar{y}}{\partial b}\)分开求导:
其中:
所以:
现在我们有了导数,也就是方向了。在我们当前w,b 的值的情况下,我们将这个导数乘上一个learning rate(也就是步长),再更新现有的w,b 值。
最后梯度下降:
梯度上升:
反向传播算法
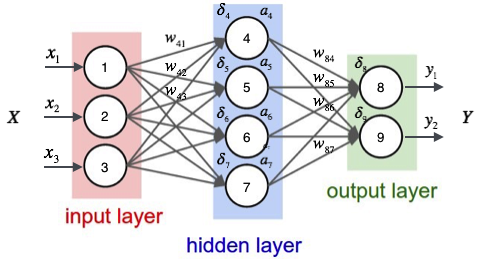
如上图,输入层有三个节点,我们将其依次编号为1、2、3;隐藏层的4个节点,编号依次为4、5、6、7;最后输出层的两个节点编号为8、9。因为我们这个神经网络是全连接网络,所以可以看到每个节点都和上一层的所有节点有连接。比如,我们可以看到隐藏层的节点4,它和输入层的三个节点1、2、3之间都有连接,其连接上的权重分别为\(w_{41},w_{42},w_{42}\),然后\(a_{4}\)是这个节点4的输出值,也就是后面8,9节点的输入值。
下面计算下\(a_{4}\)的值:
为了计算节点4的输出值,我们必须先得到其所有上游节点(也就是节点1、2、3)的输出值。节点1、2、3是输入层的节点,所以,他们的输出值就是输入向量\(\vec{x}\)本身。按照上图画出的对应关系,我们用下标代表输入层节点标识,前面的数字就是目标节点的标识,4567,后面的数字是自身节点的标识,就是123,我们要求输入向量的维数和输入层神经元个数相同,所以输入层123的输入向量就是:
这里激活函数就用\(sigmoid\),所以:
同样,我们可以继续计算出节点5、6、7的输出值。这样,隐藏层的4个节点的输出值\(a_{4},a_{5},a_{6},a_{7}\)就计算完成了,我们就可以接着计算输出层的节点8的输出值\(y_{1}\):
向前传播
神经网络实际上就是一个输入向量\(\vec{x}\)到输出向量\(\vec{y}\)的函数,即上面\(wx+b→a;aw+b→y;\)的过程。
误差的反向传播(Back Propagation,即BP算法)
现在,我们需要知道一个神经网络的每个连接上的权值是如何得到的。我们可以说神经网络是一个模型,那么这些权值就是模型的参数,也就是模型要学习的东西。然而,一个神经网络的连接方式、网络的层数、每层的节点数这些参数,则不是学习出来的,而是人为事先设置的。对于这些人为设置的参数,我们称之为超参数(Hyper-Parameters)。
误差的反向传播,简称反向传播,是指根据前向输出与真实值的误差/损失,递归应用链式法则来计算权重的梯度的这种方法。常用于人工神经网络进行梯度下降。
\(E_d\)表示样本d的误差,\(w_{ji}\)表示节点\(i\)到节点\(j\)的连接权重,\(net_{j}\)表示节点\(j\)的加权输入,\(a_{j}\)表示节点\(j\)的输出。
例:\({net}_4=w_{41}x_{41}+w_{42}x_{42}+w_{43}x_{43}+b;a_4=sigmoid(w_{41}x_{41}+w_{42}x_{42}+w_{43}x_{43}+b)\)
然后使用随机梯度下降算法对目标函数进行优化:
观察上图,我们发现权重\(w_{ji}\)仅能通过影响节点\(j\)的输入值影响网络的其它部分,\(net_{j}\)是节点的加权输入,即
\(net_{j}=\)是\(w_{ji}\)的函数。根据链式求导法则,可以得到:
对于\(\frac{\partial E_d}{\partial w_{ji}}\)的推导,需要区分输出层和隐藏层两种情况。
反向传播算法输出层的推导
输出层权值训练
对于输出层来说,\(net_{j}\)仅能通过节点\(j\)的输出值\(\bar{y}_{j}\)来影响网络其它部分,也就是说\(E_{d}\)是\(\bar{y}_{j}\)的函数,而\(\bar{y}_{j}\)是的\(net_{j}\)函数,其中\(\bar{y}_{j}=sigmoid(net_{j})\)。所以我们可以再次使用链式求导法则:
考虑上式第一项:
考虑上式第二项:
因为\(y=sigmoid(x)\)的导数就是\(y'=y(1-y)\),\(\bar{y}_{j}=sigmoid(net_{j})\)所以:
将第一项和第二项带入,得到:
如果令\(\delta=-\frac{\partial E_d}{\partial net_{j}}\),也就是一个节点的误差项\(\delta\)是网络误差对这个节点输入的偏导数的相反数。带入上式,得到:
将上述推导带入随机梯度下降公式,得到:
反向传播算法隐藏层的推导
隐藏层权值训练
现在我们要推导出隐藏层的\(\frac{\partial E_d}{\partial net_{j}}\)。
我们假设节点\(J\)的所有节点是集合\(list(j)\),例如,对于节点4来说,它的直接下游节点是节点8、节点9。可以看到\(net_{j}\)只能通过影响\(list(j)\),来影响\(E_{d}\),
所以设\(net_{k}\)是节点\(J\)的下游节点的输入,则\(E_{d}\)是\(net_{k}\)的函数,而\(net_{k}\)是\(net_{j}\)的函数。因为有多个,我们应用全导数公式,可以做出如下推导:
因为\(\delta_{j}=-\frac{\partial E_d}{\partial net_{j}}\),带入上式得到:
反向传播流程
先看图

对于输出层节点\(i\):
其中,\(\delta_{i}\)是节点的误差项,\(\bar{y}_{i}\)是节点\(i\)的输出值,\(y_{i}\)是样本对应于节点的目标值。举个例子,根据上图,对于输出层节点8来说,它的输出值是\(\bar{y}_{i}\)(图中标的是\(y_{i}\)),而样本的目标值是\(y_{i}\),带入上面的公式得到节点8的误差项\(\delta_{8}\)应该是:
对于隐藏层节点:
其中,\(a_{i}\)是节点\(i\)的输出值,\(w_{ki}\)是节点\(i\)到它的下一层节点\(j\)的连接的权重,\({\delta}_k\)是节点\(i\)的下一层节点的误差项。例如,对于隐藏层节点4来说,计算方法如下:
最后,更新每个连接上的权值:
其中,\(w_{ji}\)是节点\(i\)到节点\(j\)的权重,\(\eta\)是一个成为学习速率的常数,\(\delta_{j}\)是节点的误差项,\(x_{ji}\)是节\(i\)传递给节点\(j\)的输入。例如,权重\(w_{84}\)的更新方法如下:
类似的,权重\(w_{41}\)的更新方法如下:
偏置项的更新:
总结一句话通过误差的反向传播确定网络参数
为什么要用反向传播算法呢?
至于为什么会提出反向传播算法,我直接应用梯度下降(Gradient Descent)不行吗?想必大家肯定有过这样的疑问。答案肯定是不行的,纵然梯度下降神通广大,但却不是万能的。梯度下降可以应对带有明确求导函数的情况,或者说可以应对那些可以求出误差的情况,比如逻辑回归(Logistic Regression),我们可以把它看做没有隐层的网络;但对于多隐层的神经网络,输出层可以直接求出误差来更新参数,但其中隐层的误差是不存在的,因此不能对它直接应用梯度下降,而是先将误差反向传播至隐层,然后再应用梯度下降,其中将误差从末层往前传递的过程需要链式法则(Chain Rule)的帮助,因此反向传播算法可以说是梯度下降在链式法则中的应用
代码部分
from functools import reduce
import numpy as np
# import cupy as np
from activators import SigmoidActivator
from tqdm import tqdm
# 全连接层实现类
class FullConnectedLayer(object):
def __init__(self, input_size, output_size,
activator):
'''
构造函数
input_size: 本层输入向量的维度
output_size: 本层输出向量的维度
activator: 激活函数
'''
self.input_size = input_size
self.output_size = output_size
self.activator = activator
# 权重数组W
self.W = np.random.uniform(-0.1, 0.1,
(output_size, input_size))
# 偏置项b
self.b = np.zeros((output_size, 1))
# 输出向量
self.output = np.zeros((output_size, 1))
def forward(self, input_array):
'''
前向计算
input_array: 输入向量,维度必须等于input_size
'''
# 式2
self.input = input_array
self.output = self.activator.forward(
np.dot(self.W, input_array) + self.b)
def backward(self, delta_array):
'''
反向计算W和b的梯度
delta_array: 从上一层传递过来的误差项
'''
# 式8
print(self.W)
self.delta = self.activator.backward(self.input) * np.dot(
self.W.T, delta_array)
self.W_grad = np.dot(delta_array, self.input.T)
self.b_grad = delta_array
def update(self, learning_rate):
'''
使用梯度下降算法更新权重
'''
self.W += learning_rate * self.W_grad
self.b += learning_rate * self.b_grad
def dump(self):
print('W: %s\nb:%s' % (self.W, self.b))
# 神经网络类
class Network(object):
def __init__(self, layers):
'''
构造函数
'''
self.layers = []
for i in range(len(layers) - 1):
self.layers.append(
FullConnectedLayer(
layers[i], layers[i + 1],
SigmoidActivator()
)
)
def predict(self, sample):
'''
使用神经网络实现预测
sample: 输入样本
'''
output = sample
for layer in self.layers:
layer.forward(output)
output = layer.output
return output
def train(self, labels, data_set, rate, epoch):
'''
训练函数
labels: 样本标签
data_set: 输入样本
rate: 学习速率
epoch: 训练轮数
'''
for i in range(epoch):
for d in tqdm(range(len(data_set)),desc = 'epoch %d' % i):
self.train_one_sample(labels[d],
data_set[d], rate)
def train_one_sample(self, label, sample, rate):
self.predict(sample)
self.calc_gradient(label)
self.update_weight(rate)
def calc_gradient(self, label):
delta = self.layers[-1].activator.backward(
self.layers[-1].output
) * (label - self.layers[-1].output)
for layer in self.layers[::-1]:
layer.backward(delta)
delta = layer.delta
return delta
def update_weight(self, rate):
for layer in self.layers:
layer.update(rate)
def dump(self):
for layer in self.layers:
layer.dump()
def loss(self, output, label):
return 0.5 * ((label - output) * (label - output)).sum()
def gradient_check(self, sample_feature, sample_label):
'''
梯度检查
network: 神经网络对象
sample_feature: 样本的特征
sample_label: 样本的标签
'''
# 获取网络在当前样本下每个连接的梯度
self.predict(sample_feature)
self.calc_gradient(sample_label)
# 检查梯度
epsilon = 10e-4
for fc in self.layers:
for i in range(fc.W.shape[0]):
for j in range(fc.W.shape[1]):
fc.W[i, j] += epsilon
output = self.predict(sample_feature)
err1 = self.loss(sample_label, output)
fc.W[i, j] -= 2 * epsilon
output = self.predict(sample_feature)
err2 = self.loss(sample_label, output)
expect_grad = (err1 - err2) / (2 * epsilon)
fc.W[i, j] += epsilon
print('weights(%d,%d): expected - actural %.4e - %.4e' % (
i, j, expect_grad, fc.W_grad[i, j]))
from bp import train_data_set
def transpose(args):
return list(map(
lambda arg: list(map(
lambda line: np.array(line).reshape(len(line), 1)
, arg))
, args
))
class Normalizer(object):
def __init__(self):
self.mask = [
0x1, 0x2, 0x4, 0x8, 0x10, 0x20, 0x40, 0x80
]
def norm(self, number):
data = list(map(lambda m: 0.9 if number & m else 0.1, self.mask))
return np.array(data).reshape(8, 1)
def denorm(self, vec):
binary = list(map(lambda i: 1 if i > 0.5 else 0, vec[:, 0]))
for i in range(len(self.mask)):
binary[i] = binary[i] * self.mask[i]
return reduce(lambda x, y: x + y, binary)
def train_data_set():
normalizer = Normalizer()
data_set = []
labels = []
for i in range(0, 256):
n = normalizer.norm(i)
data_set.append(n)
labels.append(n)
return labels, data_set
def correct_ratio(network):
normalizer = Normalizer()
correct = 0.0;
for i in range(256):
if normalizer.denorm(network.predict(normalizer.norm(i))) == i:
correct += 1.0
print('correct_ratio: %.2f%%' % (correct / 256 * 100))
def test():
labels, data_set = transpose(train_data_set())
net = Network([8, 3, 8])
rate = 0.5
mini_batch = 20
epoch = 10
for i in range(epoch):
net.train(labels, data_set, rate, mini_batch)
print('after epoch %d loss: %f' % (
(i + 1),
net.loss(labels[-1], net.predict(data_set[-1]))
))
rate /= 2
correct_ratio(net)
def gradient_check():
'''
梯度检查
'''
labels, data_set = transpose(train_data_set())
net = Network([8, 3, 8])
net.gradient_check(data_set[0], labels[0])
return net


 浙公网安备 33010602011771号
浙公网安备 33010602011771号