开拓计划5 - 树状数组
开拓计划5 - 树状数组
树状数组的概念
- Q:什么是树状数组?
- A:树状数组是一种小型的把数组上的节点的和抽象成数组的数据结构。
- Q:树状数组有什么用?
- A:树状数组可以在 \(O_{\log n}\) 的时间复杂度内完成单点修改和区间查询的操作。
树状数组的原理
- Q:树状数组的原理是什么?
- A:树状数组是将前 \(2^k\) 个数的数字和记录在第 \(2^k\) 个格子,如下图
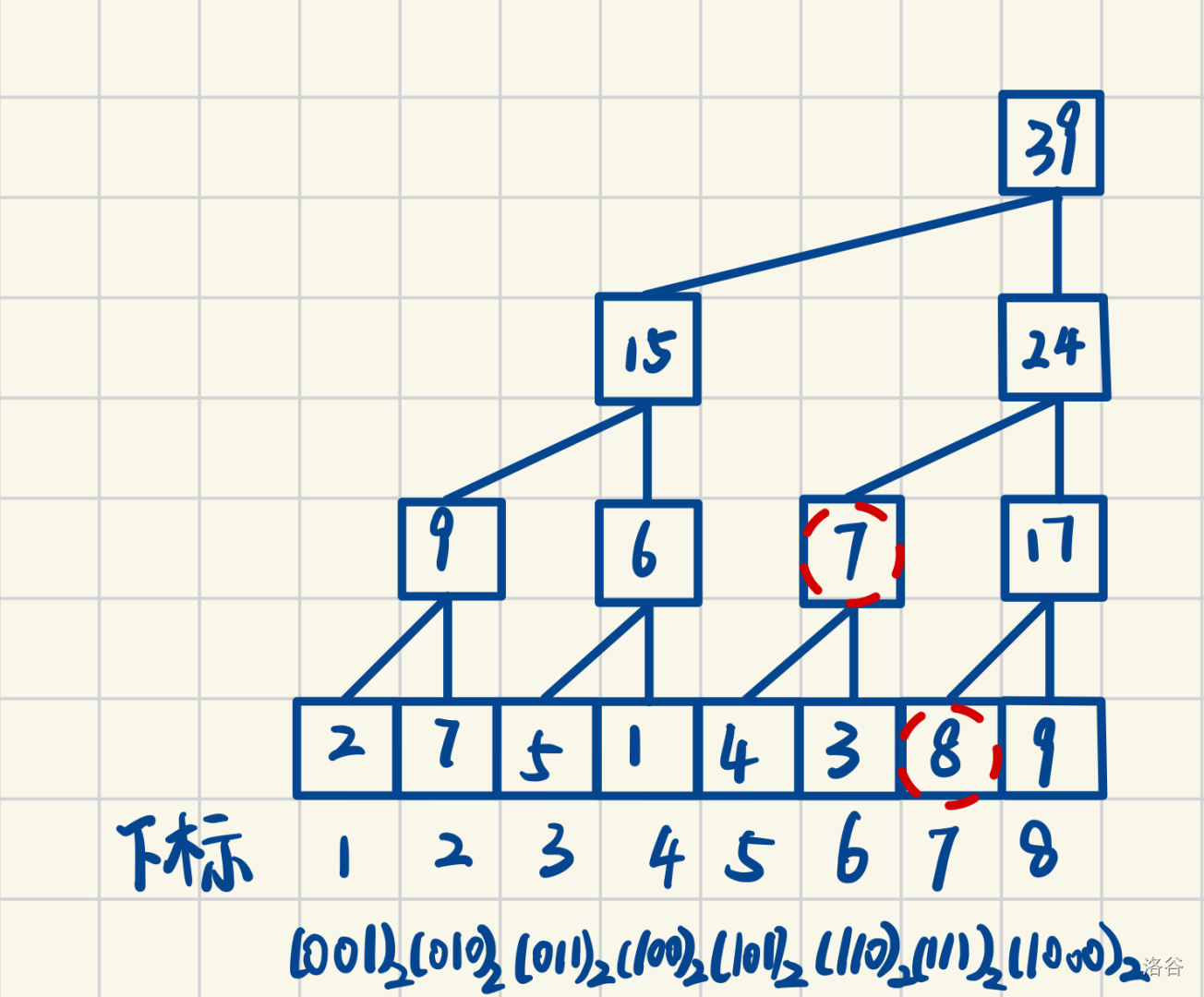
当我们要查找前 \(7\) 个数的和时,需要先查 \(7\) 自己,再查前 \(6\) 个数的数字和。
-
Q:如何做到从 \(7\) 查到 \(6\) ?
-
A:用
lowbit函数,当一个数要查询时,每次它,再减掉二进制的最低位,二进制的最低位可以通过lowbit函数得到。
int lowbit(int x){return x&-x;}
因为原数的相反数用补码存储,先变成反码时,\(x \operatorname{and} -x\text{的反码} =0\) 因为每一位都会取反。当 \(+1\) 变成补码时,最低的 \(0\) 已经变成了 \(1\) 会产生进位,进位进完后,\(\operatorname{and}\) 就能找到最低的二进制位。
- Q:如何修改?
- A:如果要修改第 \(x\) 位的值,就从第 \(x\) 位开始,将包含 \(x\) 的数字和全部更新,相当于每次 \(+\operatorname{lowbit}(x)\)。
树状数组模板代码
int tree[100005];
int lowbit(int x){return x&-x;};
void modify(int x,int y){for(int i=x;i<=n;i+=lowbit(i)) tree[i]+=y;}
int getsum(int x){
int ans=0;
for(int i=x;i>0;i-=lowbit(i)) ans+=tree[i];
return ans;
}
树状数组的应用
- 差分树状数组:区间修改,单点查询。
- 二维树状数组:单点修改,矩形查询。
注意事项
在 modify 函数中到底需要更新到几,是每一次都必须要注意的,如果因为更新次数出错导致树状数组不能正常运行,调试时间会大大加长,因此应当在写树状数组之前想清楚其含义,尽量避免出现此类情况。
NKOJ 1321 数列操作
思路:模板
NKOJ 3702 打鼹鼠
思路:模板
注意事项
- 注意下标从 \(0\) 开始,不要越界到 \(-1\) 了。
树状数组求逆序对
- Q:如何用树状数组求逆序对个数?
- A:对于一个数组从前往后遍历,把一个数的出现次数用树状数组存下来,要找当前比 \(x\) 小的数的个数只需要查前 \(x\) 个数的前缀和,如果在遍历到一个数加入一个数,就能求出在 \(x\) 前面比 \(x\) 小的有多少个。
- Q:树状数组求逆序对与用归并排序求逆序对有什么区别?
- A:树状数组只能求出逆序对的个数,但是可以让数组动态变化。归并排序可以求出具体每一个逆序对,但是数组不能有变化,一旦有变化就要全部重新求。
NKOJ 3697 乒乓比赛
思路:树状数组求逆序对
实现方法
- 如果第 \(i\) 个人要当裁判,能举办的场数是
\[i\text{左边比}i\text{小的}\times i\text{右边比}i\text{大的}+i\text{左边比}i\text{大的}\times i\text{右边比}i\text{小的}
\]
上面四样东西均能用正反两次求逆序对搞定。
NKOJ 1908 【线段树】星
思路:树状数组求逆序对
实现方法
- 明显这道题是求二维逆序对,但仔细看题目发现, \(y\) 坐标已经排好序了,所以只需要一维逆序对求出比自己 \(y\) 坐标小,并且 \(x\) 坐标也比自己小的星星的个数就是当前星星的等级。
NKOJ 3709 走丢的奶牛
思路:二分+树状数组求逆序对
实现方法
-
容易看出一头牛的编号等于左边比它小的牛的数量加右边比它小的牛的数量。
-
使用二分确定每一头牛的编号,通过刚刚发现的性质来判断当前的
mid是否可行。 -
只要从右往左确定,就可以通过逆序队得到右边比
mid编号小的牛数量。 -
二分结束后更新答案,更新树状数组。
树状数组的区间修改+区间查询
原理
- Q:如何使用树状数组实现同时区间修改、区间查询?
- A:我们定义一个差分数组 \(D\) ,当要查询 \(a_1+a_2+a_3+\cdots +a_n\) 时只需要查询
\[\begin{aligned}
a_1+a_2+a_3+\cdots+a_n &= D_1+(D_1+D_2)+(D_1+D_2+D_3)+\cdots+(D_1+D_2+D_3+\cdots D_n)\\
&=D_1+D_2+D_3+\cdots+D_n+D_2\times1+D_3\times2+D_4\times3+\cdots D_n\times(n-1)\\
&=\sum_{i=1}^{n} D_i+\sum_{i=1}^{n} D_i\times(i-1)
\end{aligned}
\]
我们将区间查询和前缀和联系了起来,这样就能使用两个树状数组分别维护 \(+\) 号前后两个数,就可以做到快速的区间修改+区间查询。
模板
#include<cstdio>
#define int long long
using namespace std;
int n;
int tree1[1000005],tree2[1000005];
int lowbit(int x){return x&-x;}
void modify1(int x,int y){for(int i=x;i<=1000000;i+=lowbit(i)) tree1[i]+=y;}
void modify2(int x,int y){for(int i=x;i<=1000000;i+=lowbit(i)) tree2[i]+=y;}
int getsum1(int x){
int ans=0;
for(int i=x;i>0;i-=lowbit(i)) ans+=tree1[i];
return ans;
}
int getsum2(int x){
int ans=0;
for(int i=x;i>0;i-=lowbit(i)) ans+=tree2[i];
return ans;
}
void update(int l,int r,int d){
modify1(l,d);
modify1(r+1,-d);
modify2(l,d*(l-1));
modify2(r+1,-d*r);
}
int query(int l,int r){return r*getsum1(r)-getsum2(r)-(l-1)*getsum1(l-1)+getsum2(l-1);}


 浙公网安备 33010602011771号
浙公网安备 33010602011771号