开拓计划21/2025集训作业表3 - 倍增&ST表&LCA&次小生成树

开拓计划21/2025集训作业表3 - 倍增&ST表&LCA&次小生成树

倍增&ST表

概念

• Q：倍增是什么？
• A：倍增，顾名思义是成倍增长的意思，它利用了二进制的性质和预处理（俗称打表）的思想，在 \(O(\log n)\) 内完成一些操作。
• Q：ST表是什么？
• A：ST表主要用于解决RMQ（区间最值问题），它用了打表的思想，但是没有将表打完整。

ST表的原理

在实现 RMQ 问题时，我们可以通过打表来提升效率。提前计算出 \([l,r]\) 的答案。但是这样打表就需要 \(O(n^2)\) 实在是太浪费时间了。于是我们发现，表没必要打得这么详细，我们设 \(f_{i,j}\) 表示区间 \([i,i+2^j-1]\) 的最大值。

预处理：

• \(f_{i,0}=a_i\)
• \(f_{i,j}=\max(f_{i,j-1},f_{i+2^{j-1},j-1})\)
• 时间复杂度 \(O(n \log n)\)

查询：

• 如果要查询区间 \([l,r]\)，先找 \(2^j \le r-l+1\) 中 \(j\) 的最大值。
  \(\therefore j=\lfloor \log_2(r-l+1) \rfloor\)
• \(ans=\max(f_{l,j},f_{r-2^j+1,j})\)
• 时间复杂度 \(O(n)\)

ST表的代码

#include<bits/stdc++.h>
using namespace std;
const int N=25005;
int f[N][35];
int main(){
	ios::sync_with_stdio(0);
	cin.tie(0),cout.tie(0);
	int n,q;
	cin>>n>>q;
	for(int i=1;i<=n;i++) cin>>f[i][0];
	int mx=log2(n);
	//预处理
	for(int j=1;j<=mx;j++){
		int i,k=(1<<j-1);
		for(i=1;i<=n-k;i++) f[i][j]=min(f[i][j-1],f[i+k][j-1]);
		for(;i<=n;i++) f[i][j]=f[i][j-1];
	}
	//查询
	for(int i=1;i<=q;i++){
		int l,r;
		cin>>l>>r;
		int j=log2(r-l+1);
		cout<<min(f[l][j],f[r-(1<<j)+1][j])<<"\n";
	}
	
	return 0;
}

LCA

概念

• Q：LCA 是什么？
• A：LCA是指树上最近公共祖先，如下图所示，\(7\) 和 \(5\) 的 LCA 就是\(2\)。
  

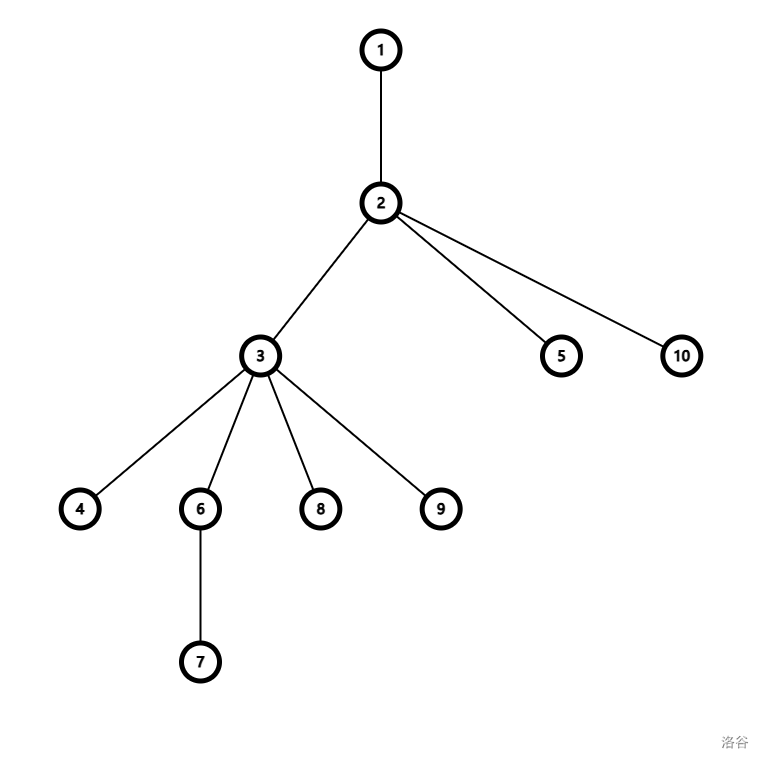
求法

倍增法

还是要求 \(7\) 和 \(5\) 的LCA。
设 \(f_{i,j}\) 表示第 \(i\) 个节点，跳 \(2^j\) 步的时候跳到的位置，\(x\) 和 \(y\) 分别为 \(5\) 和 \(7\) 的指针。
分为两个阶段：

• 第一阶段：将 \(7\) 和 \(5\) 的指针调整到同一高度。
  • 通过已经预处理的 \(f\) 数组开始尝试跳，如果高度大了就是条过头了，回去重新跳，直到 \(x\) 的新高度小于 \(y\)，就往上跳，跳完了再继续跳，直到高度一样。
• 第二阶段
  • 两个指针同时开始向上跳，跳过头了就回来，直到跳到同一个点。

倍增求LCA的代码

void dfs(int x,int fa){
	dep[x]=dep[fa]+1;
	f[x][0]=fa;
	for(int j=1;;j++){
		f[x][j]=f[f[x][j-1]][j-1];
		if(f[x][j]==0){
			mx=max(mx,j-1);
			break;
		}
	}
	for(auto i:vt[x]){
		if(i!=fa) dfs(i,x);
	}
}
int Lca(int x,int y){
	if(dep[x]<dep[y]) swap(x,y);
	for(int j=mx;j>=0;j--){
		if(dep[f[x][j]]>=dep[y]) x=f[x][j];
	}
	if(x==y) return x;
	for(int j=mx;j>=0;j--){
		if(f[x][j]!=f[y][j]) x=f[x][j],y=f[y][j];
	}
	return f[x][0];
}

次小生成树

非严格次小生成树

思路：

• 先用 kurskal 求最小生成树。
• 枚举最小生成树以外的边，将每一条边分别加入再减掉原来的最大边。
• 求所有结果的最小值。

代码：

#include<bits/stdc++.h>
#define int long long
using namespace std;
const int N=100005;
int dep[N],f[N][35],fa[N],used[N<<1],dis[N][35];
int n,m,Ans=0;
struct node{int s,e,w;}edge[N<<1];
struct nodf{int v,e;};
bool cmp(node a,node b){return a.w<b.w;}
vector<nodf> vt[N];
void dfs(int x,int fa){
	for(int j=1;(1<<j)<=dep[x];j++){
		f[x][j]=f[f[x][j-1]][j-1];
		dis[x][j]=max(dis[f[x][j-1]][j-1],dis[x][j-1]);
	}
	for(auto i:vt[x]){
		if(i.v!=fa){
			dep[i.v]=dep[x]+1;
			f[i.v][0]=x;
			dis[i.v][0]=i.e;
			dfs(i.v,x);
		}
	}
}
int Lca(int x,int y){
	int mx=0;
	if(dep[x]<dep[y]) swap(x,y);
	for(int j=30;j>=0;j--){
		if(dep[x]-(1<<j)>=dep[y]){
			mx=max(dis[x][j],mx);
			x=f[x][j];
		}
	}
	if(x==y) return mx;
	for(int j=30;j>=0;j--){
		if(f[x][j]!=f[y][j]){
			mx=max(dis[x][j],mx);
			mx=max(dis[y][j],mx);
			x=f[x][j],y=f[y][j];
		}
	}
	return max(mx,max(dis[x][0],dis[y][0]));
}
int getf(int x){
	if(x==fa[x]) return x;
	return fa[x]=getf(fa[x]); 
}
bool kurskal(){
	int cnt=0;
	for(int i=1;i<=m;i++){
		if(cnt==n-1) return 0;
		if(getf(edge[i].s)!=getf(edge[i].e)){
			cnt++;
			fa[getf(edge[i].s)]=getf(edge[i].e);
			used[i]=1;
			Ans+=edge[i].w;
			vt[edge[i].s].push_back({edge[i].e,edge[i].w});
			vt[edge[i].e].push_back({edge[i].s,edge[i].w});
		}
	}
	return 1;
}
signed main(){
	ios::sync_with_stdio(0);
	cin.tie(0),cout.tie(0);
	cin>>n>>m;
	for(int i=1;i<=n;i++) fa[i]=i;
	for(int i=1;i<=m;i++) cin>>edge[i].s>>edge[i].e>>edge[i].w;
	sort(edge+1,edge+1+m,cmp);
	if(kurskal()){
		cout<<"Keng Die!";
		return 0;
	}
	dep[1]=1;
	dfs(1,0);
	int ans=0x7fffffff;
	for(int i=1;i<=m;i++){
		if(used[i]==0){
			ans=min(ans,Ans+edge[i].w-Lca(edge[i].s,edge[i].e));
		}
	}
	cout<<ans;
	
	return 0;
}

严格次小生成树

思路

同非严格只不过要同时维护次大值，因为相等的时候就需要换成次大值。

代码

oi wiki