[TJOI2013]松鼠聚会（切比雪夫距离）

[TJOI2013]松鼠聚会（luogu）

Solution

首先介绍题目中奇特的计算距离方法——切比雪夫距离

设两个点为 A（x1,y1）,B（x2,y2）,$\Delta x=|x1-x2|$,$\Delta y=|y1-y2|$

则A，B的切比雪夫距离为

$$QDis(A,B)=max(\Delta x,\Delta y)$$
而它们的曼哈顿距离为
$$Dis(A,B)=\Delta x+\Delta y$$

• 接下来讨论切比雪夫距离如何转化为曼哈顿距离

首先看简单的情况

下图红线为坐标系中与原点（0,0）曼哈顿距离为 6 的点的集合

 

下图红线为坐标系中与原点（0,0）切比雪夫距离为 6 的点的集合

 

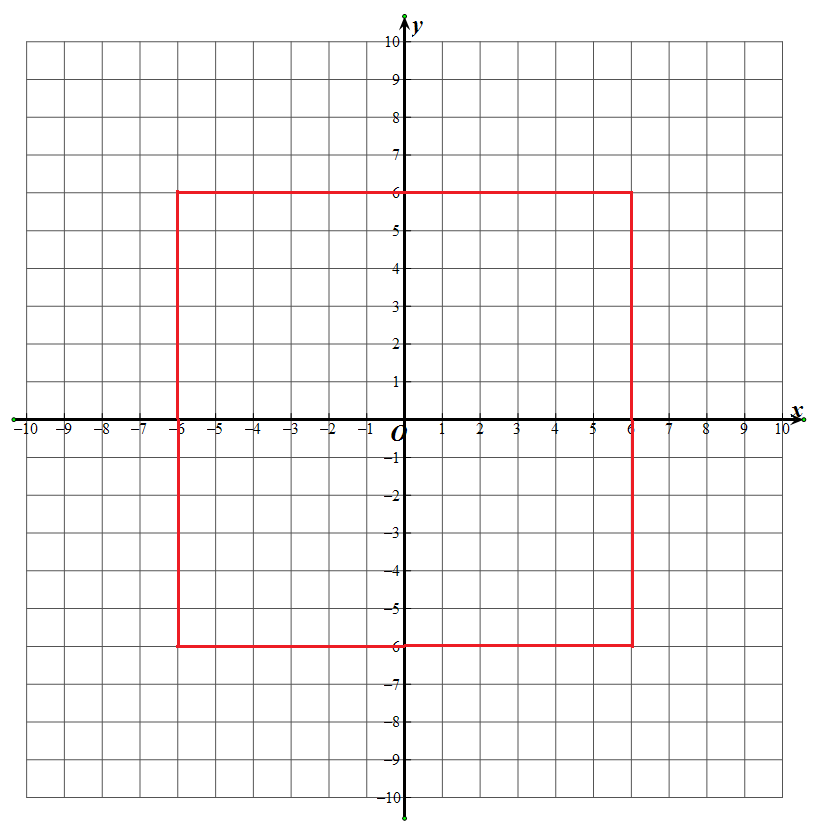
发现这两个图形都是正方形

于是对于一个定义在切比雪夫距离上的点C（x,y），将它绕原点逆时针旋转45度

得到的坐标为

$$(x*\cos\!\frac{\pi}{4}-y*\sin\!\frac{\pi}{4},y*\cos\!\frac{\pi}{4}+x*\sin\!\frac{\pi}{4})$$
根据图像，还要缩小$\frac{\sqrt{2}}{2}$

于是得到
$$(\frac{\sqrt{2}}{2}(x*\cos\!\frac{\pi}{4}-y*\sin\!\frac{\pi}{4}),\frac{\sqrt{2}}{2}(y*\cos\!\frac{\pi}{4}+x*\sin\!\frac{\pi}{4}))$$
$$=(\frac{1}{2}(x+y),\frac{1}{2}(x-y))$$

（有很多地方没有除2，但手玩一下证明也可以发现要除2，也可以先不除2，最后再除2以避免小数）

推导结束

回到原题，转化为曼哈顿距离后就十分简单了

分别对x,y排序，从两个方向各扫一遍，统计对答案的贡献

Code

 

#include <cstdio>
#include <cstdlib>
#include <algorithm>
#define ll long long
using namespace std;
const int N=1e5+10;
inline char get()
{
    static char buf[1024];
    static int pos=0,size=0;
    if(pos==size)
    {
        size=fread(buf,1,1024,stdin);
        pos=0;
        if(!size) return EOF;
        else return buf[pos++];
    }
    else return buf[pos++];     
}
int read()
{
    int sum=0,fh=1;
    char ch=get();
    while(!(ch>='0' && ch<='9'))
    {
        if(ch=='-') fh=-1;
        ch=get();
    }
    while(ch>='0' && ch<='9' && ch!=EOF) sum=sum*10+ch-48,ch=get();
    return sum*fh;
}
int n;
ll ans[N],sum;
struct node
{
    ll x,y;
    int id;
}a[N];
bool cmpx(node a,node b)
{
    return a.x<b.x;
}
bool cmpy(node a,node b)
{
    return a.y<b.y;
}
int main()
{
    n=read();
    for(int i=1;i<=n;i++)
    {
        ll x=read(),y=read();
        a[i].x=x+y,a[i].y=x-y,a[i].id=i;
    }
    sort(a+1,a+1+n,cmpx);
    for(ll i=1;i<=n;i++)
        ans[a[i].id]+=(i-1)*a[i].x-sum,sum+=a[i].x;
    sum=0;
    for(ll i=n;i;i--)
        ans[a[i].id]+=sum-(n-i)*a[i].x,sum+=a[i].x;
    sum=0;
    sort(a+1,a+1+n,cmpy);
    for(ll i=1;i<=n;i++)
        ans[a[i].id]+=(i-1)*a[i].y-sum,sum+=a[i].y;
    sum=0;
    for(ll i=n;i;i--)
        ans[a[i].id]+=sum-(n-i)*a[i].y,sum+=a[i].y;
    sum=ans[1];
    for(int i=2;i<=n;i++) sum=min(sum,ans[i]);
    printf("%lld\n",sum/2);
    return 0;
        
}