高斯消元学习笔记 & [JSOI2008]球形空间产生器

高斯消元是一种求解线性方程组的方法。

线性方程组是由 M 个 N 元一次方程共同构成的，

将它的所有系数写成一个 M 行 N 列的 “ 系数矩阵 ”，再将每个方程每个方程等号右侧的常数作为第 N + 1 列，

得到一个增广矩阵

   

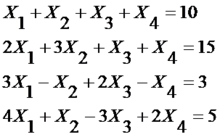
（引自360百科）

 

高斯消元的步骤是：

 

依次对于 1<=i<=n 的第 i 个元素

找到一行，满足第 1~i-1 个元素的系数为 0 ，第 i 个元素的系数不为0

把这一行交换到合适位置

用它消去除它以外每一行的第 i 个元素

 

于是最后每个 i 元素至多只有一行它的系数不为 0；

若没有这么一行（该元素为自由元），那方程组有无数组解

如果最后有一行是 0=1 的形式，则无解

伪代码：

double a[][],b[];//系数矩阵和常数

 

balabala

 

int del=0；//del表示上一个标准行（用它来消其他行的元）

for（int i=1;i<=n;i++）//当前在处理第 i 个未知数

{

　　int now=0；//可以作为下一个标准行的行

　　for(int j=del+1;j<=m;j++)

　　　　找到第 i 个元素的系数不为 0 的行作为now

　　if(!now) continue;//没找到，处理下一个元素

　　del++；

　　找到了，将 del 行与 now 行交换信息

　　for(int j=1;j<=n;j++)

　　　　if(j!=del)  对每一行消元

}

for(int i=del+1;i<=n;i++)  if(b[i]!=0) 无解

n-del为自由元的个数

 

 

---

 

 

 

[JSOI2008]球形空间产生器（luogu）

Description

题目描述

 

有一个球形空间产生器能够在 n 维空间中产生一个坚硬的球体。

现在，你被困在了这个 n 维球体中，你只知道球面上 n+1 个点的坐标，

你需要以最快的速度确定这个 n 维球体的球心坐标，以便于摧毁这个球形空间产生器。

 

输入格式

 

第一行是一个整数 n (1<=N=10)。

接下来的 n+1 行，每行有 n 个实数，表示球面上一点的 n 维坐标。

每一个实数精确到小数点后 6 位，且其绝对值都不超过 20000。

 

输出格式

有且只有一行，依次给出球心的 n 维坐标（ n 个实数），两个实数之间用一个空格隔开。

每个实数精确到小数点后 3 位。数据保证有解。你的答案必须和标准输出一模一样才能够得分。

 

Solution

设球心的坐标为（x[1],x[1],...,x[n]），其他点坐标为（a[i][1],a[i][2],...,a[i][n]）。

则对于 1~n+1 每个点有

$\prod\limits_{j=1}^{n}$(a[i][j]-x[i])^2=r

这是个n元二次方程组，我们将它们相减化成一元的形式:

对于 1 <= i <= n，有

$\prod\limits_{j=1}^{n}$2(a[i][j]-a[i+1][j])x[j]=$\prod\limits_{j=1}^{n}$(a[i][j]^2-a[i+1][j]^2)

于是可以愉快的用高斯消元了

 

Code

#include <cstdio>
#include <cstdlib>
#include <cmath>
#include <algorithm>
using namespace std;
const int N=20;
double c[N][N],a[N][N],b[N];
int n;
int main()
{
    scanf("%d",&n);
    for(int i=1;i<=n+1;i++)
        for(int j=1;j<=n;j++)
            scanf("%lf",&a[i][j]);
    for(int i=1;i<=n;i++)
        for(int j=1;j<=n;j++)
        {
            c[i][j]=2*(a[i][j]-a[i+1][j]);
            b[i]+=a[i][j]*a[i][j]-a[i+1][j]*a[i+1][j];
        }
    for(int i=1;i<=n;i++)
    {
        for(int j=i;j<=n;j++)
            if(fabs(c[j][i])>1e-8)
            {
                for(int k=1;k<=n;k++) swap(c[i][k],c[j][k]);
                swap(b[i],b[j]);
                break;
            }
        for(int j=1;j<=n;j++)
        {
            if(i==j) continue;
            double rate=c[j][i]/c[i][i];
            for(int k=1;k<=n;k++) c[j][k]-=c[i][k]*rate;
            b[j]-=b[i]*rate;
        }
    }
    for(int i=1;i<n;i++) printf("%.3lf ",b[i]/c[i][i]);
    printf("%.3lf\n",b[n]/c[n][n]);
    return 0;
}