小Z的袜子（莫队模板）

莫队

（莫队算法巧妙地将询问离线排序，使得其复杂度无比美妙……）

此处只讨论莫队的排序方法

• 按l,r排序

    bool operator <(const node &o)const
    {
        return l==o.l?r<o.r:l<o.l;
    }

发现l变化时r可能狂跳，复杂度接近O(n^2)

• 按pos[l],r排序（pos[i]：分块后i所在块）

设block为块的大小，按块排时l每变化block时r才可能狂跳

复杂度O（n*n/block）

• 奇偶性排序

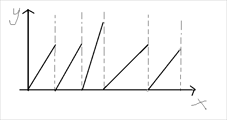
设y为r指针在的袜子编号，x为处理到的询问排序后编号，建立平面直角坐标系

（感性理解一下...）

 

两条虚线内所有pos【l】相等

发现pos[l]变化时r跳跃幅度较大

于是有了奇偶性排序

    bool operator <(const node &o)const
    {
        return pos[l]^pos[o.l]?pos[l]<pos[o.l]:pos[l]&1?r<o.r:r>o.r;
    }

 

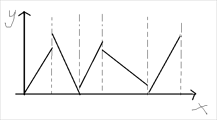
图变成这样

另外还有block=n/sqrt(m*2/3)时最快的神奇结论

 

发现一个能极大空间提高速度的技巧：

把while写成for ! ! ! 

如下

 

        for(int j=q[i-1].l;j<q[i].l;j++) del(d[j]);
        for(int j=q[i].l;j<q[i-1].l;j++) add(d[j]);
        for(int j=q[i-1].r+1;j<=q[i].r;j++) add(d[j]);
        for(int j=q[i].r+1;j<=q[i-1].r;j++) del(d[j]);

 

 

 

---

 

小Z的袜子（luogu）

Description

题目描述

作为一个生活散漫的人，小 Z 每天早上都要耗费很久从一堆五颜六色的袜子中找出一双来穿。

终于有一天，小 Z 再也无法忍受这恼人的找袜子过程，于是他决定听天由命……

具体来说，小 Z 把这 N 只袜子从 1 到 N 编号，然后从编号 L 到 R 

( 尽管小 Z 并不在意两只袜子是不是完整的一双，甚至不在意两只袜子是否一左一右，

他却很在意袜子的颜色，毕竟穿两只不同色的袜子会很尴尬。)

你的任务便是告诉小 Z，他有多大的概率抽到两只颜色相同的袜子。当然，小 Z 希望这个概率尽量高，

所以他可能会询问多个 (L,R) 以方便自己选择。

然而数据中有 L=R 的情况，请特判这种情况，输出0/1。

输入格式

输入文件第一行包含两个正整数 N 和 M。N 为袜子的数量，M 为小 Z 所提的询问的数量。

接下来一行包含 N 个正整数 C_i，其中 C_i 表示第 i 只袜子的颜色，相同的颜色用相同的数字表示。

再接下来 M 行，每行两个正整数 L, R 表示一个询问。

输出格式

包含 M 行，对于每个询问在一行中输出分数 A/B 表示从该询问的区间 [L,R] 中随机抽出两只袜子颜色相同的概率。

若该概率为 0 则输出 0/1，否则输出的 A/B 必须为最简分数。（详见样例）

Code

#include <cstdlib>
#include <cstdio>
#include <algorithm>
#include <cmath>
#define ll long long
using namespace std;
const int N=5e4+10;
int n,m,c[N],si,t,pos[N],tot;
ll s[N],ans[N][2];
struct node
{
    int l,r,id;
    bool operator <(const node &o)const
    {
        return pos[l]^pos[o.l]?pos[l]<pos[o.l]:pos[l]&1?r<o.r:r>o.r;
    }
}q[N];
ll gcd(ll a,ll b)
{
    if(a==0 || b==0) return a+b;
    else return gcd(b,a%b);
}
int main()
{
    scanf("%d%d",&n,&m);
    for(int i=1;i<=n;i++)
        scanf("%d",&c[i]);
    si=n/sqrt(m*2/3);
    t=(n+si-1)/si;
    for(int i=1;i<=t;i++)
    {
        int z=min(n,i*si);
        for(int j=(i-1)*si+1;j<=z;j++)
            pos[j]=i;
    }
    for(int i=0;i<m;i++)
    {
        scanf("%d%d",&q[tot].l,&q[tot].r);
        if(q[tot].l<q[tot].r)
        {
            ll fm=q[tot].r-q[tot].l+1;
            ans[i][0]-=fm;
            ans[i][1]=fm*(fm-1),q[tot].id=i,tot++;
        }
        else ans[i][0]=0,ans[i][1]=1;
    }
    sort(q,q+tot);
    int nl=q[0].l,nr=q[0].l;
    ll an=1;
    s[c[q[0].l]]++;
    for(int i=0;i<tot;i++)
    {
        while(nl<q[i].l) an+=1-2*s[c[nl]],s[c[nl]]--,nl++;
        while(nl-1>=q[i].l) nl--,an+=1+2*s[c[nl]],s[c[nl]]++;
        while(nr+1<=q[i].r) nr++,an+=1+2*s[c[nr]],s[c[nr]]++;
        while(nr>q[i].r) an+=1-2*s[c[nr]],s[c[nr]]--,nr--;
        ans[q[i].id][0]+=an;
    }
    for(int i=0;i<m;i++)
        if(ans[i][0]==0) puts("0/1");
        else
        {
            ll zz=gcd(ans[i][0],ans[i][1]);
            printf("%lld/%lld\n",ans[i][0]/zz,ans[i][1]/zz);
        }
    return 0;
}