A. Karen and Morning
time limit per test
2 seconds
memory limit per test
512 megabytes
input
standard input
output
standard output

Karen is getting ready for a new school day!

It is currently hh:mm, given in a 24-hour format. As you know, Karen loves palindromes, and she believes that it is good luck to wake up when the time is a palindrome.

What is the minimum number of minutes she should sleep, such that, when she wakes up, the time is a palindrome?

Remember that a palindrome is a string that reads the same forwards and backwards. For instance, 05:39 is not a palindrome, because 05:39 backwards is 93:50. On the other hand, 05:50 is a palindrome, because 05:50 backwards is 05:50.

Input

The first and only line of input contains a single string in the format hh:mm (00 ≤  hh  ≤ 23, 00 ≤  mm  ≤ 59).

Output

Output a single integer on a line by itself, the minimum number of minutes she should sleep, such that, when she wakes up, the time is a palindrome.

Examples
Input
05:39
Output
11
Input
13:31
Output
0
Input
23:59
Output
1
Note

In the first test case, the minimum number of minutes Karen should sleep for is 11. She can wake up at 05:50, when the time is a palindrome.

In the second test case, Karen can wake up immediately, as the current time, 13:31, is already a palindrome.

In the third test case, the minimum number of minutes Karen should sleep for is 1 minute. She can wake up at 00:00, when the time is a palindrome.

题意：给你一个24时制的时间 判断多少分钟后 是一个回文时间

题解：暴力

 1 #include<iostream>
 2 #include<cstdio>
 3 #include<cmath>
 4 #include<cstring>
 5 #include<algorithm>
 6 #include<map>
 7 #include<queue>
 8 #include<stack>
 9 #include<vector>
10 using namespace std;
11 int n;
12 char a[15];
13 int hh,mm;
14 int main()
15 {
16     scanf("%s",a);
17     hh=(a[0]-'0')*10+(a[1]-'0');
18     mm=(a[3]-'0')*10+(a[4]-'0');
19     for(int i=0;i<=(25*60);i++)
20     {
21         int nowmm;
22         int nowhh=hh;
23         nowmm=mm+i;
24         nowhh=nowhh+nowmm/60;
25         nowhh%=24;
26         nowmm%=60;
27         nowhh=nowhh/10+(nowhh%10)*10;
28         if(nowhh==nowmm)
29         {
30             printf("%d\n",i);
31             return 0;
32         }
33     }
34     return 0;
35 }

 

B. Karen and Coffee
time limit per test
2.5 seconds
memory limit per test
512 megabytes
input
standard input
output
standard output

To stay woke and attentive during classes, Karen needs some coffee!

Karen, a coffee aficionado, wants to know the optimal temperature for brewing the perfect cup of coffee. Indeed, she has spent some time reading several recipe books, including the universally acclaimed "The Art of the Covfefe".

She knows n coffee recipes. The i-th recipe suggests that coffee should be brewed between li and ri degrees, inclusive, to achieve the optimal taste.

Karen thinks that a temperature is admissible if at least k recipes recommend it.

Karen has a rather fickle mind, and so she asks q questions. In each question, given that she only wants to prepare coffee with a temperature between a and b, inclusive, can you tell her how many admissible integer temperatures fall within the range?

Input

The first line of input contains three integers, n, k (1 ≤ k ≤ n ≤ 200000), and q (1 ≤ q ≤ 200000), the number of recipes, the minimum number of recipes a certain temperature must be recommended by to be admissible, and the number of questions Karen has, respectively.

The next n lines describe the recipes. Specifically, the i-th line among these contains two integers li and ri (1 ≤ li ≤ ri ≤ 200000), describing that the i-th recipe suggests that the coffee be brewed between li and ri degrees, inclusive.

The next q lines describe the questions. Each of these lines contains a and b, (1 ≤ a ≤ b ≤ 200000), describing that she wants to know the number of admissible integer temperatures between a and b degrees, inclusive.

Output

For each question, output a single integer on a line by itself, the number of admissible integer temperatures between a and b degrees, inclusive.

Examples
Input
3 2 4
91 94
92 97
97 99
92 94
93 97
95 96
90 100
Output
3
3
0
4
Input
2 1 1
1 1
200000 200000
90 100
Output
0
Note

In the first test case, Karen knows 3 recipes.

  1. The first one recommends brewing the coffee between 91 and 94 degrees, inclusive.
  2. The second one recommends brewing the coffee between 92 and 97 degrees, inclusive.
  3. The third one recommends brewing the coffee between 97 and 99 degrees, inclusive.

A temperature is admissible if at least 2 recipes recommend it.

She asks 4 questions.

In her first question, she wants to know the number of admissible integer temperatures between 92 and 94 degrees, inclusive. There are 3: 92, 93 and 94 degrees are all admissible.

In her second question, she wants to know the number of admissible integer temperatures between 93 and 97 degrees, inclusive. There are 3: 93, 94 and 97 degrees are all admissible.

In her third question, she wants to know the number of admissible integer temperatures between 95 and 96 degrees, inclusive. There are none.

In her final question, she wants to know the number of admissible integer temperatures between 90 and 100 degrees, inclusive. There are 4: 92, 93, 94 and 97 degrees are all admissible.

In the second test case, Karen knows 2 recipes.

  1. The first one, "wikiHow to make Cold Brew Coffee", recommends brewing the coffee at exactly 1 degree.
  2. The second one, "What good is coffee that isn't brewed at at least 36.3306 times the temperature of the surface of the sun?", recommends brewing the coffee at exactly 200000 degrees.

A temperature is admissible if at least 1 recipe recommends it.

In her first and only question, she wants to know the number of admissible integer temperatures that are actually reasonable. There are none.

题意：给你 n个区间  q个查询[l,r] 问l~r有多少个值 属于 大于等于k个区间

题解：区间更新姿势+前缀和

 1 #include<iostream>
 2 #include<cstdio>
 3 #include<cmath>
 4 #include<cstring>
 5 #include<algorithm>
 6 #include<map>
 7 #include<queue>
 8 #include<stack>
 9 #include<vector>
10 using namespace std;
11 int n,k,q;
12 map<int,int>l;
13 int r[200010];
14 int ans[200010];
15 int main()
16 {
17     scanf("%d %d %d",&n,&k,&q);
18     int s,t;
19     l.clear();
20     for(int i=1;i<=n;i++)
21     {
22        scanf("%d %d",&s,&t);
23        l[s]++;
24        l[t+1]--;
25     }
26     int now=0;
27     for(int i=1;i<=200003;i++)
28     {
29         now+=l[i];
30         r[i]=now;
31     }
32     int jishu=0;
33     for(int i=1;i<=200003;i++)
34     {
35         if(r[i]>=k)
36             jishu++;
37         ans[i]=jishu;
38     }
39     for(int i=1;i<=q;i++)
40     {
41         scanf("%d %d",&s,&t);
42         printf("%d\n",ans[t]-ans[s-1]);
43     }
44     return 0;
45 }

 

C. Karen and Game
time limit per test
2 seconds
memory limit per test
512 megabytes
input
standard input
output
standard output

On the way to school, Karen became fixated on the puzzle game on her phone!

The game is played as follows. In each level, you have a grid with n rows and m columns. Each cell originally contains the number 0.

One move consists of choosing one row or column, and adding 1 to all of the cells in that row or column.

To win the level, after all the moves, the number in the cell at the i-th row and j-th column should be equal to gi, j.

Karen is stuck on one level, and wants to know a way to beat this level using the minimum number of moves. Please, help her with this task!

Input

The first line of input contains two integers, n and m (1 ≤ n, m ≤ 100), the number of rows and the number of columns in the grid, respectively.

The next n lines each contain m integers. In particular, the j-th integer in the i-th of these rows contains gi, j (0 ≤ gi, j ≤ 500).

Output

If there is an error and it is actually not possible to beat the level, output a single integer -1.

Otherwise, on the first line, output a single integer k, the minimum number of moves necessary to beat the level.

The next k lines should each contain one of the following, describing the moves in the order they must be done:

  • row x, (1 ≤ x ≤ n) describing a move of the form "choose the x-th row".
  • col x, (1 ≤ x ≤ m) describing a move of the form "choose the x-th column".

If there are multiple optimal solutions, output any one of them.

Examples
Input
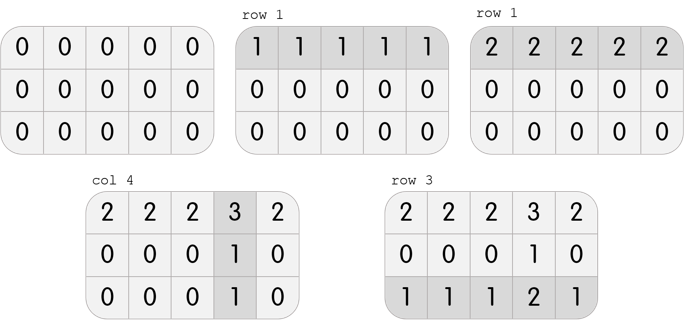
3 5
2 2 2 3 2
0 0 0 1 0
1 1 1 2 1
Output
4
row 1
row 1
col 4
row 3
Input
3 3
0 0 0
0 1 0
0 0 0
Output
-1
Input
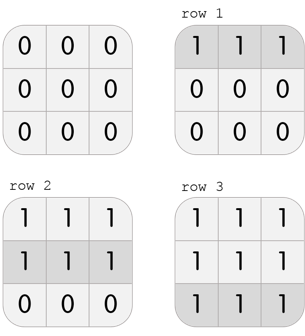
3 3
1 1 1
1 1 1
1 1 1
Output
3
row 1
row 2
row 3
Note

In the first test case, Karen has a grid with 3 rows and 5 columns. She can perform the following 4 moves to beat the level:

In the second test case, Karen has a grid with 3 rows and 3 columns. It is clear that it is impossible to beat the level; performing any move will create three 1s on the grid, but it is required to only have one 1 in the center.

In the third test case, Karen has a grid with 3 rows and 3 columns. She can perform the following 3 moves to beat the level:

Note that this is not the only solution; another solution, among others, is col 1, col 2, col 3.

题意：给你一个n*m的矩阵 现在希望用最少的操作 每次操作能使得某一行或者某一列全部减少1  输出最小的操作数 以及操作的过程 无法实现则输出-1

题解：先处理行再处理列 先处理列再处理行 暴力跑两遍  取最优；

  1 #include<iostream>
  2 #include<cstdio>
  3 #include<cmath>
  4 #include<cstring>
  5 #include<algorithm>
  6 #include<map>
  7 #include<queue>
  8 #include<stack>
  9 #include<vector>
 10 using namespace std;
 11 int n,m;
 12 int a[105][105];
 13 int b[105][105];
 14 int ans[100005];
 15 int re[100005];
 16 int ans1[100005];
 17 int re1[100005];
 18 int  main()
 19 {
 20     scanf("%d %d",&n,&m);
 21     for(int i=1; i<=n; i++)
 22     {
 23         for(int j=1; j<=m; j++)
 24         {
 25             scanf("%d",&a[i][j]);
 26             b[i][j]=a[i][j];
 27         }
 28     }
 29     int jishu=1;
 30     for(int i=1; i<=n; i++)
 31     {
 32         int minx=505;
 33         for(int j=1; j<=m; j++)
 34             minx=min(minx,a[i][j]);
 35         for(int j=1; j<=minx; j++)
 36         {
 37             ans[jishu]=1;
 38             re[jishu]=i;
 39             jishu++;
 40         }
 41         for(int j=1; j<=m; j++)
 42         {
 43             a[i][j]-=minx;
 44         }
 45     }
 46     for(int i=1; i<=m; i++)
 47     {
 48         int minx=505;
 49         for(int j=1; j<=n; j++)
 50         {
 51             minx=min(minx,a[j][i]);
 52         }
 53         for(int j=1; j<=minx; j++)
 54         {
 55             ans[jishu]=2;
 56             re[jishu]=i;
 57             jishu++;
 58         }
 59         for(int j=1; j<=n; j++)
 60         {
 61             a[j][i]-=minx;
 62         }
 63     }
 64     int flag1=1;
 65     for(int i=1; i<=n; i++)
 66     {
 67         for(int j=1; j<=m; j++)
 68         {
 69             if(a[i][j]!=0)
 70             {
 71                 flag1=0;
 72                 break;
 73             }
 74         }
 75     }
 76 
 77 
 78     for(int i=1; i<=n; i++)
 79     {
 80         for(int j=1; j<=m; j++)
 81         {
 82             a[i][j]=b[i][j];
 83         }
 84     }
 85     int jish=1;
 86     for(int i=1; i<=m; i++)
 87     {
 88         int minx=505;
 89         for(int j=1; j<=n; j++)
 90         {
 91             minx=min(minx,a[j][i]);
 92         }
 93         for(int j=1; j<=minx; j++)
 94         {
 95             ans1[jish]=2;
 96             re1[jish]=i;
 97             jish++;
 98         }
 99         for(int j=1; j<=n; j++)
100         {
101             a[j][i]-=minx;
102         }
103     }
104     for(int i=1; i<=n; i++)
105     {
106         int minx=505;
107         for(int j=1; j<=m; j++)
108         {
109             minx=min(minx,a[i][j]);
110         }
111         for(int j=1; j<=minx; j++)
112         {
113             ans1[jish]=1;
114             re1[jish]=i;
115             jish++;
116         }
117         for(int j=1; j<=m; j++)
118         {
119             a[i][j]-=minx;
120         }
121     }
122     int flag2=1;
123     for(int i=1; i<=n; i++)
124     {
125         for(int j=1; j<=m; j++)
126         {
127             if(a[i][j]!=0)
128             {
129                 flag2=0;
130                 break;
131             }
132         }
133     }
134     if(flag1==0&&flag2==0)
135     {
136         printf("-1\n");
137         return 0;
138     }
139     if(flag1==1&&flag2==1)
140     {
141         if(jishu<jish)
142         {
143             printf("%d\n",jishu-1);
144             for(int i=1; i<jishu; i++)
145             {
146                 if(ans[i]==1)
147                     printf("row ");
148                 else
149                     printf("col ");
150                 printf("%d\n",re[i]);
151             }
152         }
153         else
154         {
155             printf("%d\n",jish-1);
156             for(int i=1; i<jish; i++)
157             {
158                 if(ans1[i]==1)
159                     printf("row ");
160                 else
161                     printf("col ");
162                 printf("%d\n",re1[i]);
163             }
164         }
165         return 0;
166     }
167     if(flag1==1)
168     {
169         printf("%d\n",jishu-1);
170         for(int i=1; i<jishu; i++)
171         {
172             if(ans[i]==1)
173                 printf("row ");
174             else
175                 printf("col ");
176             printf("%d\n",re[i]);
177         }
178         return 0;
179     }
180     if(flag2==1)
181     {
182         printf("%d\n",jish-1);
183         for(int i=1; i<jish; i++)
184         {
185             if(ans1[i]==1)
186                 printf("row ");
187             else
188                 printf("col ");
189             printf("%d\n",re1[i]);
190         }
191     }
192     return 0;
193 }
194 /*
195 3 2
196 1 1
197 2 2
198 2 2
199 2 3
200 2 1 2
201 2 1 2
202 */