Noora is a student of one famous high school. It's her final year in school — she is going to study in university next year. However, she has to get an «A» graduation certificate in order to apply to a prestigious one.
In school, where Noora is studying, teachers are putting down marks to the online class register, which are integers from 1 to k. The worst mark is 1, the best is k. Mark that is going to the certificate, is calculated as an average of all the marks, rounded to the closest integer. If several answers are possible, rounding up is produced. For example, 7.3 is rounded to 7, but 7.5 and 7.8784 — to 8.
For instance, if Noora has marks [8, 9], then the mark to the certificate is 9, because the average is equal to 8.5 and rounded to 9, but if the marks are [8, 8, 9], Noora will have graduation certificate with 8.
To graduate with «A» certificate, Noora has to have mark k.
Noora got n marks in register this year. However, she is afraid that her marks are not enough to get final mark k. Noora decided to ask for help in the internet, where hacker Leha immediately responded to her request. He is ready to hack class register for Noora and to add Noora any number of additional marks from 1 to k. At the same time, Leha want his hack be unseen to everyone, so he decided to add as less as possible additional marks. Please help Leha to calculate the minimal number of marks he has to add, so that final Noora's mark will become equal to k.
The first line contains two integers n and k (1 ≤ n ≤ 100, 1 ≤ k ≤ 100) denoting the number of marks, received by Noora and the value of highest possible mark.
The second line contains n integers a1, a2, ..., an (1 ≤ ai ≤ k) denoting marks received by Noora before Leha's hack.
Print a single integer — minimal number of additional marks, that Leha has to add in order to change Noora's final mark to k.
2 10
8 9
4
3 5
4 4 4
3
Consider the first example testcase.
Maximal mark is 10, Noora received two marks — 8 and 9, so current final mark is 9. To fix it, Leha can add marks [10, 10, 10, 10] (4 marks in total) to the registry, achieving Noora having average mark equal to 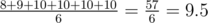 . Consequently, new final mark is 10. Less number of marks won't fix the situation.
. Consequently, new final mark is 10. Less number of marks won't fix the situation.
In the second example Leha can add [5, 5, 5] to the registry, so that making average mark equal to 4.5, which is enough to have 5 in the certificate.
题意:给你n个数 以及k 增加ans个k使得 n+ans个数的平均数四舍五入的值为k 输出最小的ans
题解:暴力ans
1 #include<iostream> 2 #include<cstdio> 3 #include<cmath> 4 #include<cstring> 5 #include<queue> 6 #include<map> 7 #include<vector> 8 #include<algorithm> 9 #define ll __int64 10 using namespace std; 11 int n,k; 12 int exm=0,sum=0; 13 int main() 14 { 15 exm=0; 16 scanf("%d %d",&n,&k); 17 for(int i=1;i<=n;i++){ 18 scanf("%d",&exm); 19 sum+=exm; 20 } 21 for(int i=0;i<100000;i++) 22 { 23 double what; 24 what=(double)(sum+k*i)/(n+i); 25 if(what>=double(k-0.5)) 26 { 27 printf("%d\n",i); 28 return 0; 29 } 30 } 31 return 0; 32 }
Summer holidays! Someone is going on trips, someone is visiting grandparents, but someone is trying to get a part-time job. This summer Noora decided that she wants to earn some money, and took a job in a shop as an assistant.
Shop, where Noora is working, has a plan on the following n days. For each day sales manager knows exactly, that in i-th day ki products will be put up for sale and exactly li clients will come to the shop that day. Also, the manager is sure, that everyone, who comes to the shop, buys exactly one product or, if there aren't any left, leaves the shop without buying anything. Moreover, due to the short shelf-life of the products, manager established the following rule: if some part of the products left on the shelves at the end of the day, that products aren't kept on the next day and are sent to the dump.
For advertising purposes manager offered to start a sell-out in the shop. He asked Noora to choose any f days from n next for sell-outs. On each of f chosen days the number of products were put up for sale would be doubled. Thus, if on i-th day shop planned to put up for sale ki products and Noora has chosen this day for sell-out, shelves of the shop would keep 2·ki products. Consequently, there is an opportunity to sell two times more products on days of sell-out.
Noora's task is to choose f days to maximize total number of sold products. She asks you to help her with such a difficult problem.
The first line contains two integers n and f (1 ≤ n ≤ 105, 0 ≤ f ≤ n) denoting the number of days in shop's plan and the number of days that Noora has to choose for sell-out.
Each line of the following n subsequent lines contains two integers ki, li (0 ≤ ki, li ≤ 109) denoting the number of products on the shelves of the shop on the i-th day and the number of clients that will come to the shop on i-th day.
Print a single integer denoting the maximal number of products that shop can sell.
4 2
2 1
3 5
2 3
1 5
10
4 1
0 2
0 3
3 5
0 6
5
In the first example we can choose days with numbers 2 and 4 for sell-out. In this case new numbers of products for sale would be equal to [2, 6, 2, 2] respectively. So on the first day shop will sell 1 product, on the second — 5, on the third — 2, on the fourth — 2. In total 1 + 5 + 2 + 2 = 10 product units.
In the second example it is possible to sell 5 products, if you choose third day for sell-out.
题意:给你n,f 以及n天的在售物品和顾客的情况 现在可以选择f天 将在售物品的数量翻倍 问如何选择 使得能够卖出的物品数量最大 输出这个值
题解:sort
1 #include<iostream> 2 #include<cstdio> 3 #include<cmath> 4 #include<cstring> 5 #include<queue> 6 #include<map> 7 #include<vector> 8 #include<algorithm> 9 #define ll __int64 10 using namespace std; 11 struct node 12 { 13 ll k,l,we; 14 }N[100005]; 15 int n,f; 16 bool cmp(struct node aa,struct node bb) 17 { 18 return aa.we>bb.we; 19 } 20 int main() 21 { 22 scanf("%d %d",&n,&f); 23 ll a,b; 24 ll exm=0; 25 for(int i=1;i<=n;i++){ 26 scanf("%I64d %I64d",&a,&b); 27 if(a>=b){ 28 exm+=b; 29 N[i].k=2*a-b;; 30 N[i].l=0; 31 N[i].we=0; 32 } 33 else{ 34 exm+=a; 35 N[i].k=a; 36 N[i].l=b-a; 37 N[i].we=min(a,b-a); 38 } 39 } 40 sort(N+1,N+1+n,cmp); 41 for(int i=1;i<=f;i++) 42 exm+=N[i].we; 43 printf("%I64d\n",exm); 44 return 0; 45 }
Leha decided to move to a quiet town Vičkopolis, because he was tired by living in Bankopolis. Upon arrival he immediately began to expand his network of hacked computers. During the week Leha managed to get access to n computers throughout the town. Incidentally all the computers, which were hacked by Leha, lie on the same straight line, due to the reason that there is the only one straight street in Vičkopolis.
Let's denote the coordinate system on this street. Besides let's number all the hacked computers with integers from 1 to n. So the i-th hacked computer is located at the point xi. Moreover the coordinates of all computers are distinct.
Leha is determined to have a little rest after a hard week. Therefore he is going to invite his friend Noora to a restaurant. However the girl agrees to go on a date with the only one condition: Leha have to solve a simple task.
Leha should calculate a sum of F(a) for all a, where a is a non-empty subset of the set, that consists of all hacked computers. Formally, let's denote A the set of all integers from 1 to n. Noora asks the hacker to find value of the expression 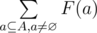 . Here F(a) is calculated as the maximum among the distances between all pairs of computers from the set a. Formally,
. Here F(a) is calculated as the maximum among the distances between all pairs of computers from the set a. Formally, 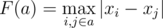 . Since the required sum can be quite large Noora asks to find it modulo 109 + 7.
. Since the required sum can be quite large Noora asks to find it modulo 109 + 7.
Though, Leha is too tired. Consequently he is not able to solve this task. Help the hacker to attend a date.
The first line contains one integer n (1 ≤ n ≤ 3·105) denoting the number of hacked computers.
The second line contains n integers x1, x2, ..., xn (1 ≤ xi ≤ 109) denoting the coordinates of hacked computers. It is guaranteed that all xi are distinct.
Print a single integer — the required sum modulo 109 + 7.
2
4 7
3
3
4 3 1
9
There are three non-empty subsets in the first sample test: ,
, 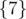 and
and 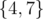 . The first and the second subset increase the sum by 0 and the third subset increases the sum by 7 - 4 = 3. In total the answer is 0 + 0 + 3 = 3.
. The first and the second subset increase the sum by 0 and the third subset increases the sum by 7 - 4 = 3. In total the answer is 0 + 0 + 3 = 3.
There are seven non-empty subsets in the second sample test. Among them only the following subsets increase the answer: 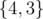 ,
, 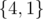 ,
, 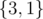 ,
, 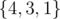 . In total the sum is (4 - 3) + (4 - 1) + (3 - 1) + (4 - 1) = 9.
. In total the sum is (4 - 3) + (4 - 1) + (3 - 1) + (4 - 1) = 9.
题意:给你n个值 处理序列的所有子集 将所有子集的权值求和输出 权值的定义:当前集合中最大值与最小值的差值
题解:先将原序列排序 写出所有的子集 以及集合中对权值贡献的最大值以及最小值 统计每个数输出的次数 可以发现规律;
1 #include<iostream> 2 #include<cstdio> 3 #include<cmath> 4 #include<cstring> 5 #include<queue> 6 #include<map> 7 #include<vector> 8 #include<algorithm> 9 #define ll __int64 10 #define mod 1000000007 11 using namespace std; 12 int n; 13 ll a[300005]; 14 ll er[300005]; 15 int main() 16 { 17 scanf("%d",&n); 18 for(int i=1; i<=n; i++) 19 scanf("%I64d",&a[i]); 20 ll e=1; 21 er[0]=1; 22 for(int i=1; i<=n; i++){ 23 e*=2; 24 e%=mod; 25 er[i]=e; 26 } 27 sort(a+1,a+1+n); 28 ll sum1=0,sum2=0; 29 for(int i=n; i>=1; i--) 30 sum1=(sum1+(er[i-1]-1)*a[i]%mod)%mod; 31 for(int i=n; i>=1; i--) 32 sum2=(sum2+(er[n-i]-1)*a[i]%mod)%mod; 33 printf("%I64d\n",(sum1-sum2+mod)%mod); 34 return 0; 35 }


 浙公网安备 33010602011771号
浙公网安备 33010602011771号