隐私保护集合求交

隐私保护集合求交

隐私保护集合求交（Private Set Intersection,PSI）是这样的一类问题：有两个参与方P1、P2分别拥有两个集合X、Y，现在这两个参与方想要在不透露彼此的各自拥有的集合信息的前提下即P1不知晓Y的任何额外信息，P2也不知晓X的任何额外信息，求得X与Y的交集。尽管可以利用通用MPC协议来实现PSI，但是针对PSI这一特定问题有更高效的专用协议---利用OPRF协议实现的PSZZ方案。

1. 定义

先将后面需要用到的定义描述如下：

定义	解释
\(OPRF\)	OPRF协议
\(PRF\)	伪随机函数
\(PSZZ\)	PSZZ协议
\(k_i\)	第i个OPRF协议中PRF所使用的密钥
\(t_j\),\(q_j\)	T矩阵的第j行，U矩阵的第j行
\(s\)	发送方在OPRF协议中的选择比特
\(r\)	接收方在OPRF中的选择比特
\(Cockoo\ hash\)	布谷鸟hash
\(B\ Stash\)	Cockoo hash中的存放元素的箱子和暂存区
\(H\)	hash函数
\(C\)	伪随机编码

2. OPRF

2.1 PRF

在介绍OPRF之间需要先介绍一下PRF协议。伪随机函数（Pseudo Random Function，PRF)是相对于真随机函数(Random Function,RF)而言的。

简要描述一下RF:对于一个函数F，其本质是一个映射，将一个输入集合X\(\rightarrow\)输出集合Y有很多种方式(其总数为\(m^n\),假设\(|X|=m,|Y|=n\))，所谓Random是指从𝐹={𝑓|𝑓:𝑋→𝑌}均匀随机的选取一个\(f\),对于一个特定的输入\(x_i\in X\)得到\(f(x_i)=y\in Y\)。

PRF是指现在有一个密钥\(k\)去选择F集合中的第\(k\)个\(f\),并不是均匀随机选取的，为了保证为随机性还需准备另一个\(f'\)是均匀随机选取的\(f\).当P1拥有密钥\(k\),P2拥有输入\(x_i\),双方执行PRF协议时P2无法区分PRF的输出\(f(x_i)\)是由P1通过自己的密钥\(k\)选取的\(f_k\)计算得到的\(f_k(x_i)\)还是由\(f'\)计算得到的\(f'(x_i)\)

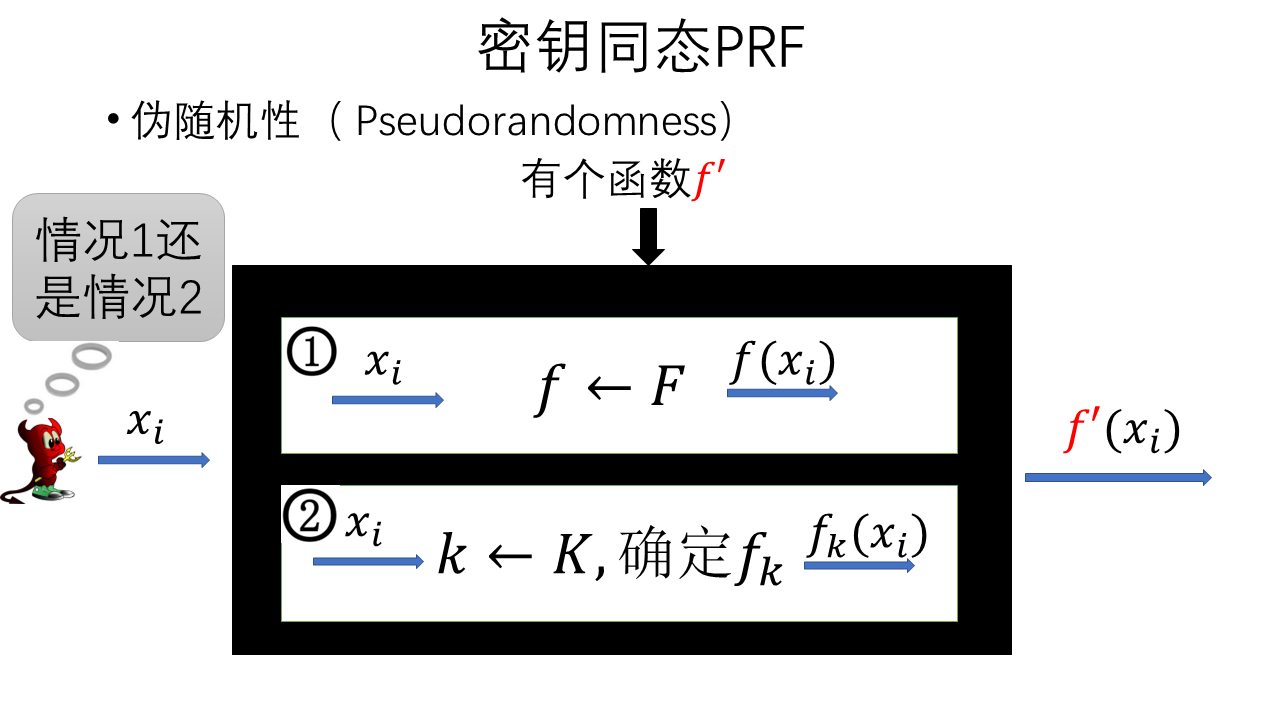
PRF的形式化定义为：

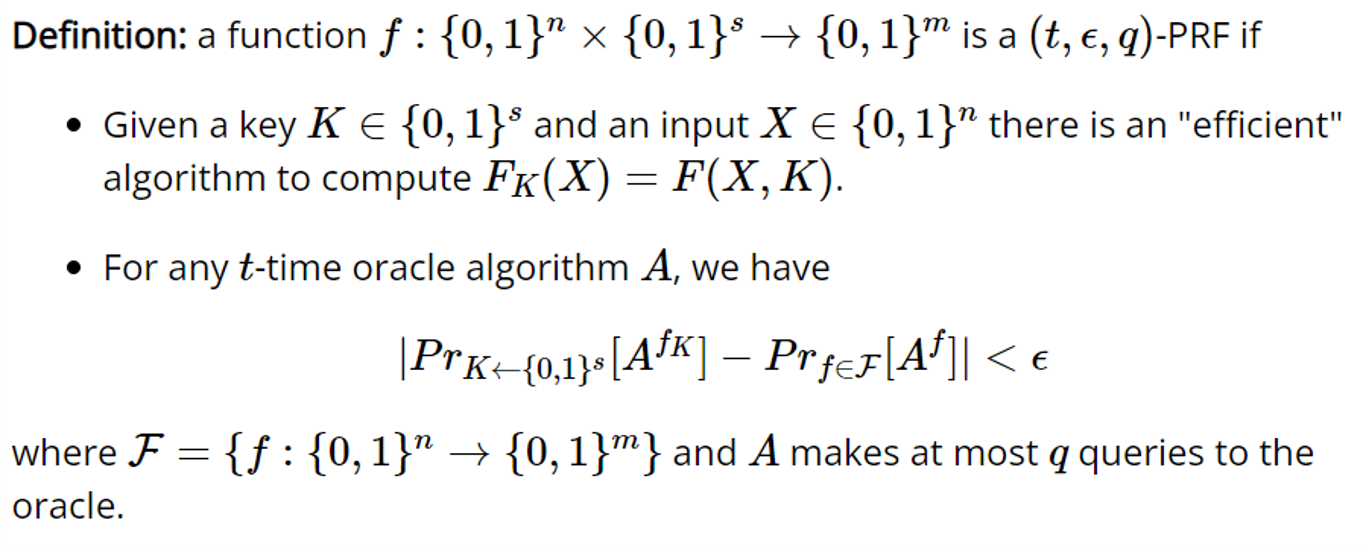
2.2 OPRF

了解了PRF之后就很容易明白OPRF：OPRF是一个MPC协议，允许两个参与方对一个PRF的F求值，其中一方持有密钥\(k\),另一方持有PRF的输入\(x\),协议令第二个参与方得到\(F_k(x)\)。

3. 布谷鸟哈希

布谷鸟哈希(Cuckoo Hasing)是Pagh 和 Rodler在2004年提出的，Cuckoo Hash是一种散列方法并不是密码学中的Hash函数，但其使用的散列值是由密码学Hash函数求得的。Cuckoo将一个含有n个元素的集合X放置在一个比n大的可容纳b个元素的固定大小的空箱子\(B\)中以及一个大小不定的暂存区中。其基本思想是：针对每一个\(x_i\in X\)，计算三个hash值\(h_1(x_i),h_2(x_i),h_3(x_i)\),如果\(B[h_1(x_i)],B[h_2(x_i)],B[h_3(x_i)]\)有一个空位置，就将\(x_i\)放置在该空位置上，若三个位置都不空则随机剔除一个位置上的元素，将\(x_i\)放置在该位置上，然后迭代插入被剔除的元素，若迭代一定次数后仍然没有将这个被剔除的元素放置在箱子中则将其放在缓冲区中，这也是Cuckoo的由来。

算法的主要执行流程：

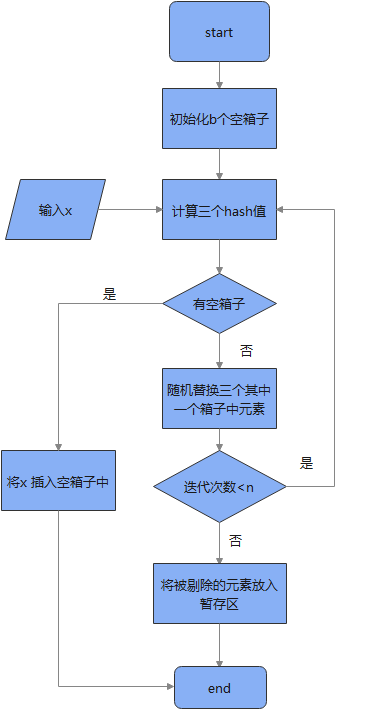
布谷鸟hash更详细的描述在这篇博客里面有：https://www.cnblogs.com/pam-sh/p/16047585.html

4. PSSZ方案

PSSZ利用了Cockoo Hash，OPRF ，OT 扩展协议来完成PSI，强烈依赖于OPRF协议。

方案描述：

• 参数：两个参与方P1，P2。其中P1拥有输入集合X,P2拥有输入集合Y。|Y|=|X|=n

• 执行过程：

1. P2运用Cockoo Hash将Y中元素放置在\(1.2n+s\)个箱子中。n是Y的大小，s是指Cockoo Hash中的暂存区大小

2. P1与P2之间执行\(1.2n+s\)个OPRF协议。P1拥有OPRF协议的私钥，P2拥有OPRF的输入。在第\(i\)个OPRF协议中，P1拥有的私钥为\(k_i\),P2的输入为\(y\in Y\),双方执行OPRF协议后P2得到\(F_{k_i}(y)\)

3. 现在P2拥有一个OPRF的输出集合OPRF-Y，OPRF-Y中的每一个元素对应Y中的每一个输入y.P1执行操作：针对每一个\(x\in X\),P1都计算一个四个值，得到两个集合H和S。对于每一个\(x\in X\),P1向\(H\)放置的三个元素为\(F_{k_{H_1(x)}}(X),F_{k_{H_2(x)}}(X),F_{k_{H_3(x)}}(X)\),其中\(H_1,H_2,H_3\)是指Cockoo hash中的三个Hash函数；P1向\(S\)中放置的元素为\(F_{k_{1.2n+j}}(X)\),\(1.2n+j\)是指元素在S中的位置，其中\(1\leq j\leq |S|\).H集合和S集合的形式化定义为：

   \[\begin{aligned} H &=\left\{F\left(k_{h_{i}(x)}, x\right) \mid x \in X \text { and } i \in\{1,2,3\}\right\} \\ S &=\left\{F\left(k_{1.2 n+j}, x\right) \mid x \in X \text { and } j \in\{1, \ldots, s\}\right\} \end{aligned} \]

   H的长度为\(3n\),S的长度为\(sn\)接下来P1将H和S发送给P2

4. P2收到H和S以后利用如下方法求得交集：对于\(y\in Y\),

   如果y被放在1.2n个箱子中，P2就在H寻找有没有y对应得OPRF-Y的输出，若有，P2将y加入交集中。

   如果y被放置在暂存区S中，P2就在S寻找有没有y对应得OPRF-Y的输出, 若有，P2将y加入交集中。

只要OPRF的输出不发生碰撞，此协议的计算结果就是正确的，并且可以抵御半诚实的参与方攻击，其安全性来自OPRF.

5. 实现

5.1 OPRF的实现

协议主要的实现在于如何去构造1.2n+s个OPRF协议，Kolesnikov等人在2016年提出了一种高效实现OPRF的协议的方案，该方案本质上就是一个OT扩展协议，协议执行的结果是构造了1.2n+s个\(\infty\)选1-OT协议。下面我将描述如何将OT协议变为OPRF，OT协议在我之前的博客有介绍：https://www.cnblogs.com/hsa0x7f/p/16477310.html

在OT扩展协议中，生成T矩阵和U矩阵的方法为：

\[\boldsymbol{t}_{j} \oplus \boldsymbol{u}_{j}=r_{j} \cdot 1^{k} \stackrel{\text { def }}{=}\left\{\begin{array}{ll} 1^{k} & \text { if } r_{j}=1 \\ 0^{k} & \text { if } r_{j}=0 \end{array}\right. \]

\(t_j,u_j\)分别表示T和U的某一行，\(r_j\)表示选择比特。这意味着\(T\oplus U\)的每一行都为全零或者全一，并且矩阵的每一行都只能实现2选1-OT协议（因为选择比特只有两种可能性）。为了实现\(\infty\)选1-OT协议，我们需要让每一个OT协议的输入选择比特为\(\infty\)多种可能性，并且其长度必须与基础OT协议的数目k相等，如何去实现这样的功能？答案是伪随机编码，更通俗的讲是一个能输出k比特长度随机数的随机预言机C。利用C我们就可以实现\(\infty\)选1-OT协议，同时T和U矩阵的定义应该修改为：

\[\boldsymbol{t}_{j} \oplus \boldsymbol{u}_{j}=C(r_{j}) \]

\(r_j\)现在是第j个OT协议的选择比特比特串，\(r_j\)可以任意长。同时，可以得到结论:

\[\boldsymbol{q}_{j}=\boldsymbol{t}_{j} \oplus\left[C\left(r_{j}\right) \cdot s\right] \]

整理得：\(\boldsymbol{t}_{j}=\boldsymbol{q}_{j} \oplus\left[C\left(r_{j}\right) \cdot s\right]\)

现在有一个关键问题是，如何从\(\infin\)选1-OT协议变换到OPRF？其实可以看到在OT协议中一方拥有\(r_j\)和\(t_j\),另一方一方拥有\(q_j\)和\(s\),直观上看\(r \mapsto H(\boldsymbol{q} \oplus[C(r) \cdot s])\)可以看作一个函数F。接受方拥有输入\(r\),只需计算\(H(t)\)作为OPRF的输出。发送方拥有密钥\(s\)和\(q\),对于任意的\(x\in X\)计算\(F_{q,s}(r)=H(\boldsymbol{q} \oplus[C(x) \cdot s])\).这样就实现了一个OPRF。通过OT实现OPRF需要有几点需要说明：

• r在PSI中就是P2的输入集合\(Y\), \(s\)是P1在执行OT协议时的选择字符串，q是P1通过OT获得的矩阵，t是P2在实行OT时生成的T矩阵。在第\(j\)个OT协议中，OPRF的输出为\(F_{q_j,s}(y)=H(\boldsymbol{q_j} \oplus[C(y) \cdot s])=H(t_j)\),\(y\in Y\),\(q_j,t_j\)分别是\(T,U\)矩阵的某一行（共1.2n+s行）即第j个协议中的密钥为\(q_j\)和s，第\(j\)个\(y\)对应的OPRF输出是\(H(t_j)\)。H是hash函数。
• 接收方接受到的为\(\boldsymbol{t}=\boldsymbol{q} \oplus[C(r) \cdot s]\),而不仅仅是\(H(\boldsymbol{t})\)
• 协议实现的多个OPRF实例中，共享了密钥\(\boldsymbol{s}\)和伪随机编码\(C\)
• 该协议仅仅适合2PC。因为在多个参与方的情况下，参与方应该只得到所有集合的交集，必须保护两两集合之间的交集信息。

5.2 我的整体实现

code:https://github.com/shenaohe/MPC
在我的实现中，有几点需要说明。

1. 实现语言为python, 使用的通信协议为Socket,两个输入集合的大小为90，基础OT协议调用数量为128，伪随机编码采用的hash函数为sha1
2. 在Cockoo hash中使用的hash函数为md5，没有采用标准的3个不同的hash函数，通过在输入后面分别添加0，1，2通过hash函数计算得到的值作为三个不同hash的输出
3. OT协议采用公钥密码学实现，采用的密码体制为RSA，p和q的长度都为128比特。

实现结果：

P1的输入集合X：0-89，即x=[b'0',b'1',...,b'89']

P2的输入集合Y：0-89，即x=[b'0',b'1',...,b'89']

协议执行server端输出：

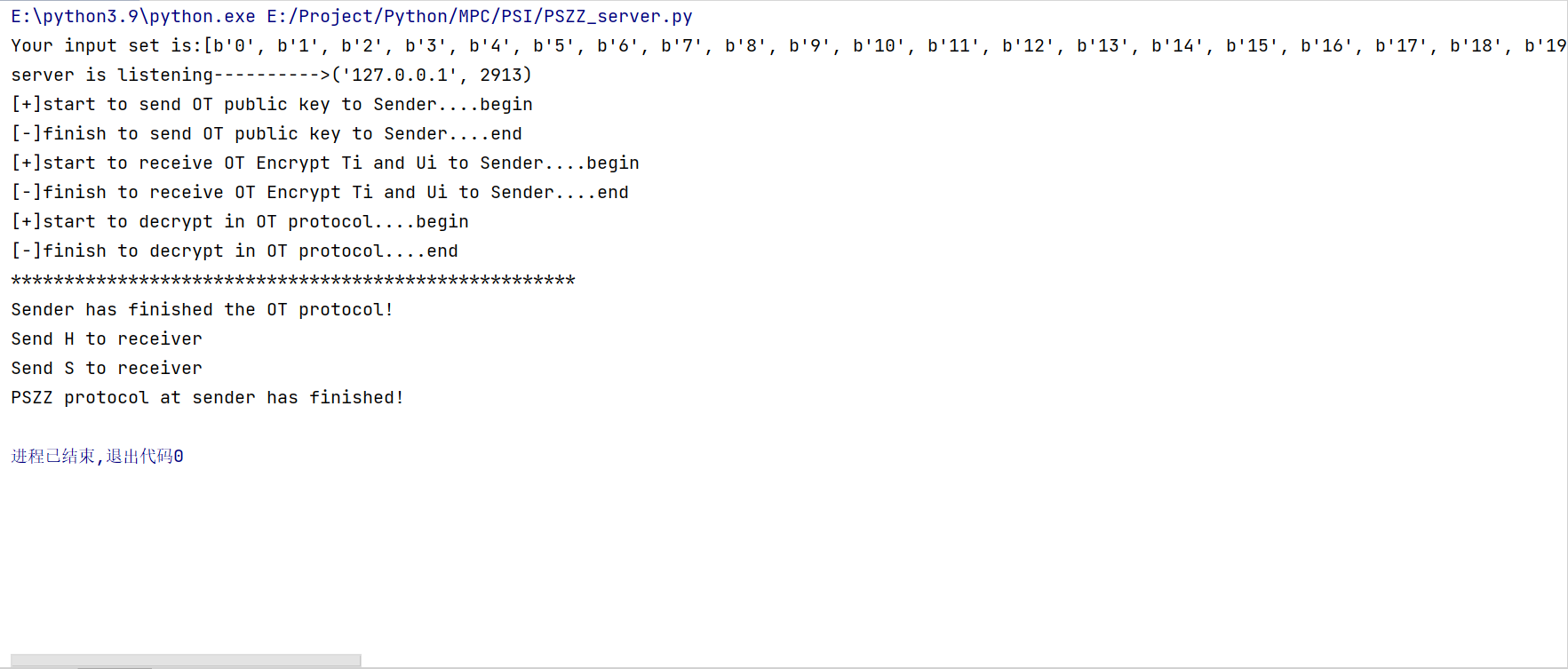
协议执行client端输出：

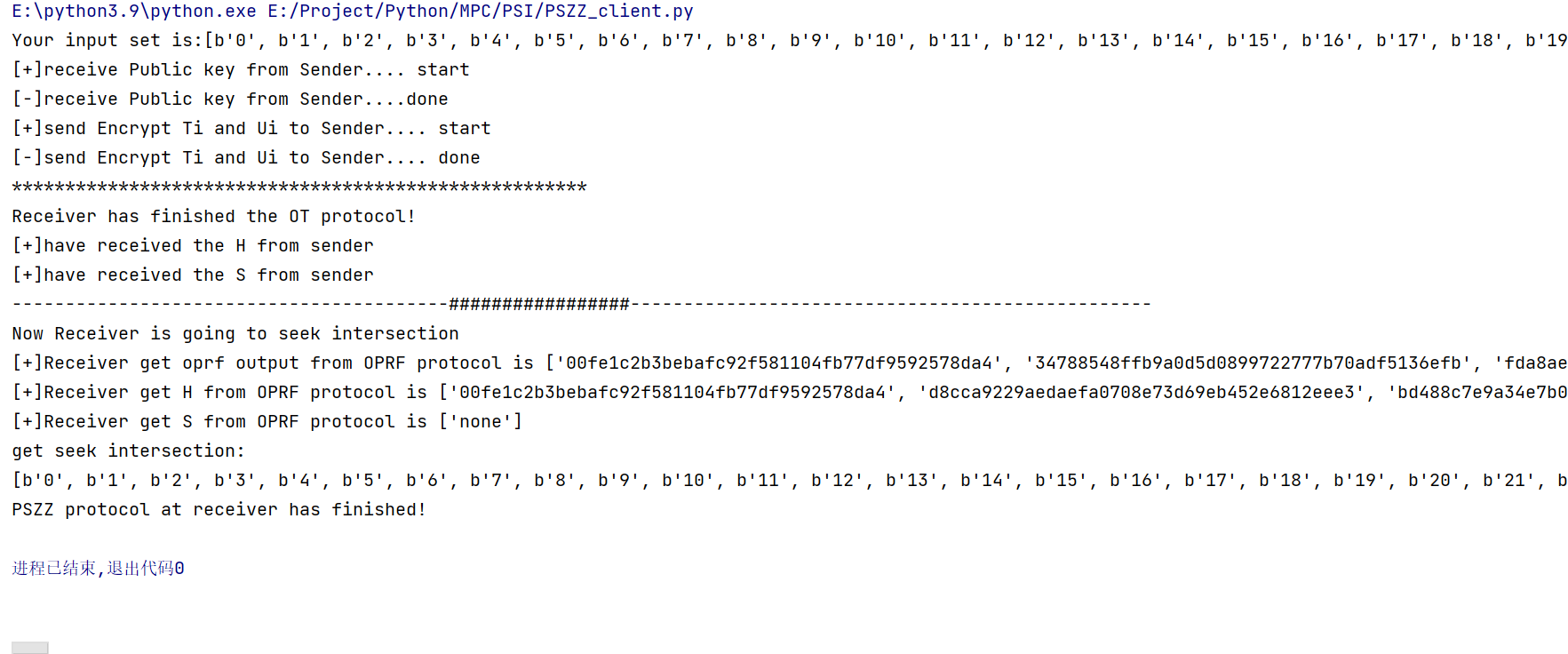
可以看到（在倒数第二行）输出结果正确。