SVD分解及线性最小二乘问题
这部分矩阵运算的知识是三维重建的数据基础。
矩阵分解
求解线性方程组:,其解可以表示为
.
为了提高运算速度,节约存储空间,通常会采用矩阵分解的方案,常见的矩阵分解有LU分解、QR分解、Cholesky分解、Schur分解、奇异分解等。这里简单介绍几种。
LU分解:如果方阵A是非奇异的,LU分解总可进行。一个矩阵可以表示为一个交换下三角矩阵和一个上三角矩阵的乘机。更整洁的形式是:一个矩阵可以表示为一个上三角矩阵和一个下三角矩阵以及一个置换矩阵的形式,即:
从而方程的解可以表示为
QR分解:矩阵可以分解为一个正交矩阵Q和一个上三角矩阵R的乘机形式。类似于LU,通常有一个正交矩阵Q,一个上三角矩阵R及一个置换矩阵E,满足:,方程的解为:
Cholesky分解:如果矩阵X是对称正定的,X可以分解为一个下三角矩阵和上三角矩阵的乘机,且下三角和上三角互为转置。
如果任何非零向量z,都有,则X为正定矩阵。虫咬条件是X的特征值全为正。
特征值分解EVD:任意n阶方阵X可以分解为XV=VD,其中D为特征值对角阵,V是特征向量矩阵。
奇异值分解SVD:任意一个m*n维的矩阵X可以分解为,其中UV为酉矩阵,S是m*n维的对角矩阵,其对角线元素为X的从大到小排序的非负奇异值。SVD分解十分强大且适用,因为任意一个矩阵都可以实现SVD分解,相比与SVD分解,特征值分解只能应用于方阵。
SVD的定义
特征值分解中,任意方阵可以有XV=VD。对于任意m*n的矩阵A,通过可以得到一个方阵,从而得到:
A的SVD分解是:
其中:U是一个m*m的正交阵,S是一个m*n的对角阵,对角元素为A的奇异值,V是一个n*n的正交阵。U的m个列向量成为A的左奇异向量,V的n个列向量称为A的右奇异向量。S完全由A决定和UV无关。
为实对称阵的特征值为
,则S中的奇异值为:
,V是
的特征向量。
在矩阵Σ中也是从大到小排列,而且σ的减少特别的快,在很多情况下,前10%甚至1%的奇异值的和就占了全部的奇异值之和的99%以上了。也就是说,我们也可以用前r大的奇异值来近似描述矩阵,这里定义一下部分奇异值分解:
三个矩阵相乘的结果将会是一个接近于A的矩阵,在这儿,r越接近于n,则相乘的结果越接近于A。
线性最小二乘问题
m个方程求解n个未知数,有三种情况:
- m=n且A为非奇异,则有唯一解,
- m>n,约束的个数大于未知数的个数,称为超定问题(overdetermined)
- m<n,负定/欠定问题(underdetermined)
通常我们遇到的都是超定问题,此时Ax=b的解是不存在的,从而转向解最小二乘问题:
J(x)为凸函数,一阶导数为0,得到:,称之为正规方程
一般解:
奇异值分解与线性最小二乘问题
这就是线性最小二乘问题的解。
特殊情况:齐次线性方程Ax=0 A的行数大于列数
此时,最小二乘解为最小特征值对应的特征向量。
感性认识:如果x是的特征向量,则目标函数:
求解方案:
,V为特征向量阵,找最小特征值对应的V中的特征向量。
,前面我们知道U是
的特征值,V是
的特征值,找S中最小奇异值对应的V的右奇异向量即可。

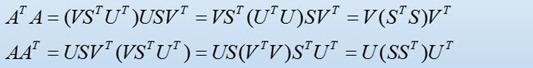


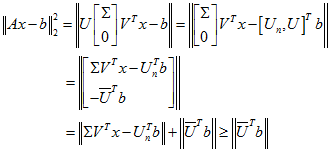

 浙公网安备 33010602011771号
浙公网安备 33010602011771号