[ACM]线段树及其扩展(动态开点,权值线段树,势能线段树,归并树,扫描线)
2.11、Segment Tree
前言:本节翻译自Segment Tree - Algorithms for Competitive Programming (cp-algorithms.com) ,有些图是自己加的,原文中的部分英文表述,我换成了更合适的中文。
如果理解不了本文中的描述,首先是本人的文字能力不足导致的,其次还可能是读者在前置知识点
递归,分治,树,二叉树的树上搜索,位运算上可能还没有理解到位。本文的主要目的是详细的介绍线段树这一知识点,所以默认读者已有以上的编程经验,如果用过多的文字来描述上述知识点就有点本末倒置了。
线段树是一种存储区间信息的数据结构,同时也是一个二叉搜索树。它能高效的查询一段区间的信息,同时还足够灵活满足修改区间信息等操作。比如查询数组中一段连续区间的和,或者在 \(\Theta(log_{}{n})\) 的时间内查询区间的最小值。除此之外线段树还允许修改数组中单个位置的信息,甚至能够同时修改整个数组。
线段树可以很容易地推广到更大的维度。比如,在二维线段树中可以在 \(\Theta(\log^2_{} {n})\) 的时间复杂度内求子矩阵的最小值或者其和。
重要的是线段树只需要线性的内存空间,长度为 \(n\) 的数组,只需花费 \(4n\) 的空间来建立线段树。
我们从建立一个最简单的线段树开始。我们想高效的求得一个数组区间内的元素和。问题的标准定义如下:
给定一个数组 \(a[0 \dots n-1]\) ,线段树要能够求的数组区间 \([l,r]\) 的总和(即计算 \(\sum^{r}_{i=l}{a[i]}\)),同时能够修改任意一个元素的值(即修改 \(a[i]=x\))。线段树需要在 \(\Theta(\log_{2}{n})\) 的时间内完成这两个操作。
这是对简单方法的改进。对于一个普通数组来说可以在 \(\Theta(1)\) 的时间内修改一个元素的值,但是求和需要 \(\Theta(n)\) 的时间。如果我们使用前缀和算法那么求和可以在 \(\Theta(1)\) 的时间内完成,但是修改一个元素的值需要 \(\Theta(n)\)的时间。
2.11.1、线段树的结构
当我们在解决数组段的时候可以采用分治的思想。
我们计算并存储整个数组中元素的和,即 \(a[0,···,n-1]\) 。 我们可以将数组划分为 \(a[0,mid]\) ,以及 \(a[mid+1,n-1]\) 其中 \(mid = \frac{0+n-1}{2}\) ,计算并存储它们的和。这两个区间又用相同的折半方式继续划分,直到区间的大小为 \(1\)。
我们可以把这些线段看成是一个完全二叉树:根节点代表区间 \(a[0,n-1]\) ,除了叶子,每个结点都有两个儿子,代表进一步划分的区间。这就是为什么这种数据结构叫做线段树(树的每个结点都代表一个段),尽管在大多数的实现代码中并没有显示的定义树的结构。下面是一个线段树的可视化表达,表示一个数组 a={ 1,3,-2,8,-7 }。
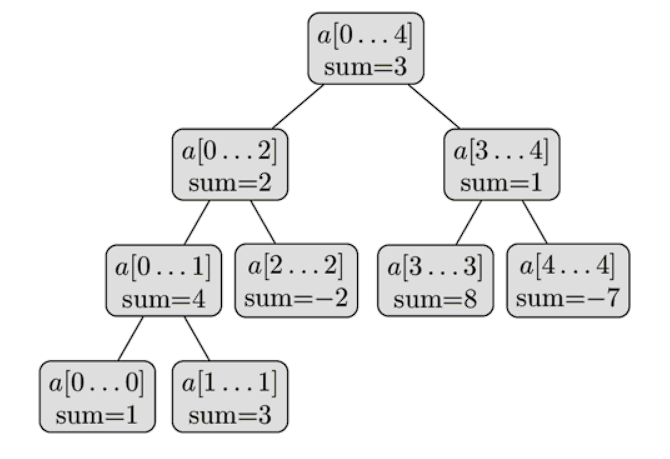
从这个线段树的简单描述中,我们可以看出线段树只需由线性个结点组成。该树的第一层有一个根节点,第二层有两个结点,第三层有4个结点,直到结点数量达到 \(n\)。因此在最坏的情况下线段树的节点可以用下面的总和来估计:
值得注意的是,当 \(n\) 不是 \(2\) 的幂次方时,线段树的最后一层将不会被填满。从上图中就可以看到这种情况。对于每一个被填满的层次,都包含了完整的 [0,n-1] 区间,层与层的区别在于划分不同,越深的层次划分的越细致,每个区间代表的长度越小。
基于以上事实,我们可以看出线段树的高度为 \(\Theta(log_{2}{n})\) ,因为从根到叶的过程中线段所代表的区间长度大约减少了一半。
2.11.2、建树
在建树之前,我们需要先决定:
- 每个结点存储什么值。比如,在求和线段树中,一个结点存储的值为区间 \([l,r]\) 中所有元素的和。
- 将线段树中的两个兄弟节点合并的操作如何进行。比如说,在求和线段树中,对于 \(a[l_1,\dots,r_1]\) 与 \(a[l_2,\dots,r_2]\) 合并为 \(a[l_1,\dots,r_2]\) 时(我们假设 \(r_1 + 1 =l_2\)),我们需要把两个结点的和加起来。
需要注意的是,在线段树中所有叶子结点都代表着原始数组(即 \(a[0,n-1]\))中的一个元素(也可以看做长度为 \(1\) 的区间)。在这些值的基础上,我们可以计算前一层的值,通过上面我们定义的合并操作。然后不断向上重复,我们就可以得到根节点的值。这是上文提到的折半划分的逆运算,被划分的两个区间信息确定后,向上合并为被划分的区间的值。
从递归的角度可以更好的描述这个过程,即从根节点递归到叶节点。在非叶子节点中,建树的过程如下:
- 递归的构造他的两个子节点。
- 合并两个子节点的值,从而构建自身这个节点。
如果递归到了叶子节点(递归的边界),即上文提到的区间长度为 \(1\) 的节点,那么我们直接把原始数组的值赋值过去就可以了(这是针对于求和线段树,对于不同的问题构造方式可能会不同)。
我们从根节点开始执行这个构造过程,所以到最后我们可以遍历到整棵树。
整个构建的时间复杂度为 \(\Theta(n)\),假设合并操作的时间为常数(合并操作被调用 \(n\) 次,这等于线段树的内部节点数)。
2.11.3、求和
现在我们需要解决区间和询问问题。对于输入的两个数字 \(l\),\(r\) 我们需要在 \(\Theta(log_{2}{n})\) 的时间复杂度内计算出区间 \(a[l,r]\) 的和。
为解决这个问题,我们需要进行树上遍历用提前计算好的区间和(在建树时存储的值)来组成我们的答案。假设我们现在遍历到了表示区间 \(a[tl \dots tr]\) 的节点上。现有以下三种情况。
-
最简单的情况便是当前所在的区间为 \([l,r]\) 的子区间,那我们直接返回答案就好了。(\(l==tl\) 且$ r==tr$ 的情况也属于这种情况)。

-
还有可能我们要查询的区间 \([l,r]\) 完全属于当前节点的左儿子所代表的区间(\(a[l,r] \in a[tl,mid]\)),或者右儿子所代表的区间(\(a[l,r] \in a[mid+1,tr]\) ,其中 \(mid = \frac{tl+tr}{2}\))。在这种情况下,我们可以直接转到相应的子节点中,并对子节点继续从这三种情况中进行处理(该过程是递归进行的)。

-
最后一种情况,查询的区间与左右儿子所代表的区间均相交。在这种情况下,我们没有其他选择,只能进行两次递归调用,每个子节点调用一次。首先我们到左子结点,计算这个节点的部分答案,然后去到右边的子节点,计算这个节点的部分答案,然后把两个答案相加。

可以看出递归的边界是 1 所对应的情况,2,3 两种情况最终都会成为情况1 在递归树中的父节点。
因此,求和查询用一个函数来处理,该函数使用左子节点或右子节点递归调用自己一次(对应上文的 2 两种情况);或者使用左子节点和右子节点递归调用自己两次(对应上文的3,将查询拆分为两个子查询)。当前所在区间成为查询区间的子区间时,直接返回在建树时预先计算好的区间和(即当前节点存储的值)。
查询区间和的过程,是一个树上遍历的过程,遍历树中所有重要的节点,使用预先计算好的区间和。这个过程的图像描述如下图。还是上文的数组 a={ 1,3,-2,8,-7 },我们现在想要计算 \(a[2,4]\) 这个区间的和。紫色对应情况3 的区间,蓝色对应情况2的区间,绿色对应情况1 的区间。灰色表示没有遍历到的区间。区间左侧文字为递归的顺序。
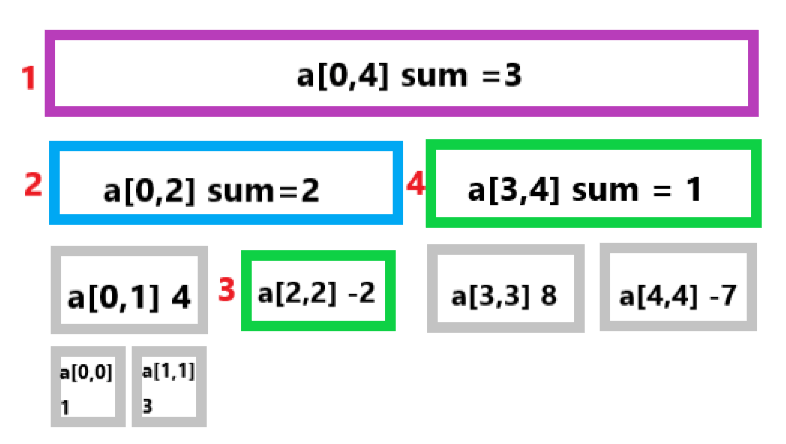
最终我们得到的结果是 \(-2+1=-1\)。
现在可以回答为什么这个算法的时间复杂度是 \(\Theta(log_{2}{n})\) 。为了展示这个复杂度,我们来看看树的每一层。可以证明,对于每一层,我们只访问不超过四个顶点。同时树的高度为 \(\Theta(log_{2}{n})\) ,总的访问个数最多为 \(4\log_{2}{n}\) ,忽略系数就是 \(\Theta(log_{2}{n})\)。
我们可以通过归纳法证明这个命题(每层最多有四个顶点)是正确的。在第一层,我们只访问一个顶点,根顶点,所以这里我们访问的顶点少于四个。现在我们来看一个任意的一层。根据归纳假设,我们最多访问四个顶点。如果我们最多只访问两个顶点,那么下一层最多有四个顶点。这是微不足道的,因为每个顶点最多只能引起两次递归调用。假设我们访问了当前层中的三到四个顶点。从这些顶点出发,我们将更仔细地分析中间的顶点。
由于查询的是连续子数组的和,这些所有的子区间组成了一条区间链,中间的部分都属于情况 1 被 [l,r] 完全覆盖,因此这些顶点不会进行任何递归调用。所以只有最左边和最右边的顶点才有可能进行递归调用(图中第二层)。这些最多只会创建四个递归调用,所以下一层也会满足这个结论。我们可以说,一个分支接近查询的左边界,第二个分支接近查询的右边界。
2.11.4、单点更新
现在我们需要完成第二个任务,修改单个结点的值,即修改原始数组中 \(a[i] = x\) (修改值或是增加值原理是一样的)。我们将会重建部分线段树,使得他符合我们修改后的数组。
单点更新操作比求和操作更加简单。由于线段树的每一层都是对整个原始数组的不同划分,因此如果修改了一个点的值,每一层有且仅有一个节点将被修改,那么时间复杂度将会是 \(\Theta(log_{2}{n})\)。
很容易看出,更新请求可以使用递归函数来实现。遍历到任意一个结点时,继续向下递归包含 \(a[i]\) 的子区间(只存在于左子区间,或者是右子区间),在回溯的时候会重新计算其和值,类似于在构建方法中完成的方式。
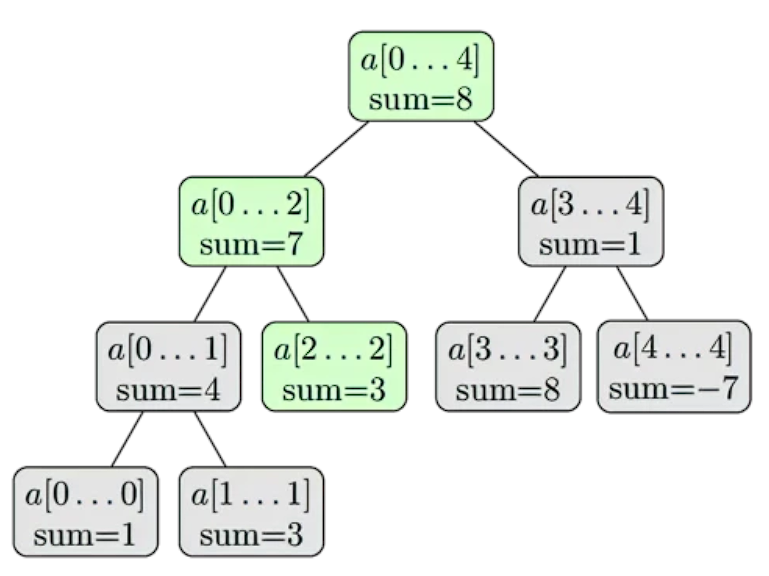
我们继续使用上面的数组 a={ 1,3,-2,8,-7 }。执行修改操作使得 \(a[2] = 3\)。三个绿色的节点将会被访问同时修改其表示的区间和的值。
2.11.5、实现
主要考虑的是如何存储线段树。当然我们可以用一个结构体来表示一个对象,这些对象存储区间的端点、区间和以及指向其子顶点的指针。然而,这需要以指针的形式存储大量冗余信息。我们将使用一个简单的技巧,通过使用隐式数据结构来提高效率:仅将总和以及所代表的区间端点存储在结构体数组中(类似用于二进制堆的方法)。
线段树节点的存储有很多的形式,这与不同人的喜好有关,本文仅介绍我自己喜欢使用的方式,即用结构体存储节点所表示的端点以及区间和。这样做的好处在于,写递归函数的时候少传递 \(2\) 个参数来表示当前访问到了那个节点,而直接从节点中取得。
下标为 \(1\) 的结构体数组存储根节点的信息,他的两个子区间的信息分别存储在下标为 \(2\),\(3\) 的位置。我们可以用 i<<1 的方式快速找到 \(i\) 节点的左儿子,用 i<<1|1 的方式快速找到 \(i\) 节点的右儿子,一个结点的父节点可以用 i>>1 的方式获取。这是非常重要的性质!
如之前提到的,线段树的总节点数要开到 \(4n\) ,可能会有多余的空间出现,但是为了不出现段错误,我们统一都初始化为 \(4n\)。
对于 \(4n\) 的解释:
- 如果 \(n\) 为 \(2\) 的幂次方,那么就不会出现有空节点的情况,存储线段树的二叉树变为满二叉树。在此情况下,线段树的节点个数为 \(2n-1\) ,有 \(n\) 个叶子节点,以及 \(n-1\) 个内部节点。
- 如果 \(n\) 不是 \(2\) 的幂次方,那么需要开 $ \lfloor log_{2}{n} \rfloor + 1 $ 层,需要多乘一个 \(2\) ,所以将会开到 \(4n\) 。
定义代码:
const int N = 1e5+10;
struct Node
{
int l,r; /// 区间端点
int sum; /// 区间和
}T[N<<2]; /// 线段树数组
int a[N]; /// 原始数组
另外,为了方便代码编写以下是我将会定义的宏:
#define ls (rt<<1) #define rs (rt<<1|1) #define L (T[rt].l) #define R (T[rt].r) #define mid ((T[rt].l + T[rt].r) >> 1)
ls表示左子区间的编号,rs表示右子区间的编号,L表示当前区间的左端点,R表示当前区间的右端点,mid表示当前区间的中间位置。
从给定 \(a[]\) 数组中构造线段树的过程如下:它是一个递归函数,参数为 rt 表示当前遍历的节点的下标,l,r 表示当前处理的节点对应的区间。在主程序中将会以 rt = 1,l = 1, r = n 被调用。if 内的代码对应的是叶子节点的处理方式,if 下面的代码对应的是非叶子节点的处理方式。
inline void push_up(int rt)
{
T[rt].sum = T[ls].sum + T[rs].sum;
}
void build(int rt,int l,int r)
{
T[rt] = {l,r,0}; /// 存储区间基本信息
if( l == r ) { /// 递归的边界,到了区间长度为 1 的子区间
T[rt].sum = a[l]; /// 将原始数组的值赋予当前区间
return ;
}
build(ls,l,mid); /// 递归的构造左子树
build(rs,mid+1,r); /// 递归的构造右子树
push_up(rt); /// 合并两个子区间的信息
}
build 函数中第一行 sum 值先赋值 \(0\) 作为临时的值,叶子结点的 sum 值由第十行赋予,非叶子节点的 sum 值由 push_up 函数赋予。需要注意的是,13,14 行的代码 ls,rs,mid 均为我定义的宏(详见上文),如果没有定义宏的话,代码将会报错。定义宏之后,代码将会更加的简洁,方便检查错误(血泪教训)。读者可以试试对比定义宏的代码,和不定义宏的代码在阅读上的体验。
求和函数也是一个递归函数,它的参数有当前处理的结点编号 rt ,所求和的区间 l,r (有些线段树的写法还有有 tl,tr 两个参数用来表示当前处理节点所对应的区间端点,但是本文的线段树结构中已经存了这两个信息,所以就不用在函数中定义这两个参数)。函数中三个 if 对应着上文提到的不同情况。第一个 if 为递归的边界,后面两个 if 将递归向下进行,搜索长度更小的区间。需要注意的是函数中 L,R,mid,ls,rs 均为宏,如果没有上文的宏定义,代码将会报错。
int range_query(int rt,int l,int r)
{
if( l <= L && r >= R ) return T[rt].sum; /// 对应情况 1
int sum = 0;
if( l <= mid ) sum += range_query(ls,l,r); /// 只进入这一个 if 为情况 2
if( r > mid ) sum += range_query(rs,l,r); /// 只进入这一个 if 为情况 2
return sum; /// 当两个 if 都进入了为 情况 3
}
最后是单点更新,这个函数有三个参数表示当前节点标号的 rt ,表示修改a[i] = x 中的 i 也就是待修改的下标 pos(这个下标是针对原始数组的),以及 val 表示 x ,即修改之后的值。
void single_update(int rt,int pos,int val)
{
if( L == R && L == val ){ /// 递归边界
T[rt].sum = val;
return ;
}
if( pos <= mid ) single_update(ls,pos,val); /// 在左子区间中
else single_update(rs,pos,val); /// 在右子区间中
push_up(rt); /// 重新合并子区间(有修改的值)
}
这里的代码结构类似于快速选择算法的 quickselection 函数。
2.11.6、小结
线段树是一颗二叉搜索树,在定义时,我们采用结构体数组的方式,而非指针节点。需要强调的是,线段树代码实现有很多版本,每个人选择自己喜欢的方式就可以了,我最开始学习线段树的时候,网上每一篇题解都用不同的风格来写,很是头痛,但是只要原理懂了,实现只是方式上的不同而已。我在上文定义的 5 个宏 L,R,mid,ls,rs 是我的编程经验,读者完全可以不用宏。
建树过程的本质是在树上进行 深度优先搜索,如果读者没有类似的编程经验,可能阅读本文会有些吃力,建议先去学习这个模块的知识。搜索到叶子节点时将会把原始数组的值赋给区间节点,回溯时会把子区间信息合并到本区间。当最后回溯到根节点(即编号为 1 的节点时)整棵树就建立完成了,每个节点都保存了它所代表的区间和以及区间的左右两个端点。
更新操作是简化的建树过程,建树时会进入两个子区间,而单点更新时只会进入其中一个,最终形成一条根节点到叶节点的路径。向下递归的过程是查找节点的过程,而向上回溯的过程是更新区间和的过程。
区间和查询操作的核心是理解三种情况,对于每个遍历到的节点我们都需要判断它属于三种情况的哪一种情况,并做出相应的处理。
push_up 函数是不必要的函数,完全可以用一行代码来代替,这也是一种编程经验,写成内联函数的形式不会影响算法的时间复杂度,还可提升代码的可读性。把相似的代码抽象成一个函数,是一个良好的编程习惯。
2.11.7、线段树的应用
线段树是一种非常灵活的数据结构,允许在许多不同的方向上进行变化和扩展。让我们试着把它们分类如下。
2.11.7.1、最大值
让我们稍微改变一下上面描述的问题的条件:现在我们将进行最大值查询,而不是查询总和。该树将具有与上述树完全相同的结构。仅把和的存储变为最大值存储,我还需要修改区间合并的方式,区间和查询将变为区间最大值查询同样要对三种情况进行处理,单点更新函数与建树函数仅需将 sum 改为 ma 就可以了。
struct Node
{
int l,r; /// 区间端点
int ma; /// 区间最大值
}T[N<<2]; /// 线段树数组
void push_up(int rt)
{
T[rt].ma = T[ls].ma>T[rs].ma?T[ls].ma:T[rs].ma;
}
int range_query(int rt,int l,int r)
{
if( l <= L && r >= R ) return T[rt].ma; /// 对应情况 1
int tema = -0x3f3f3f3f; /// 用一个很小的值来做初值
if( l <= mid ) tema = max(tema,range_query(ls,l,r) ); /// 只进入这一个 if 为情况 2
if( r > mid ) tema = max(tema,range_query(rs,l,r) ); /// 只进入这一个 if 为情况 2
return tema; /// 当两个 if 都进入了为 情况 3
}
当然,这个问题可以很容易地变成计算最小值而不是最大值。
2.11.7.2、求最大值的同时保存其出现的次数
这个任务与前一个任务非常相似。除了求最大值,我们还要求最大值出现的次数。为了解决这个问题,除了最大值之外,我们还存储了它在相应段中的出现次数。
单点更新函数与上节没有任何变化,push_up 函数为了维护新的信息做了较大修改,代码写的比较简洁可能需要多思考下。build 函数只需要在 if 中多初始化 cnt=1 就可以了。
改动最大的是查询最大值函数,并为了代码简洁我们新加了一个combine 函数来维护查询的答案(如果不这样做的话,在后面两个 if 中会有很多重复代码,形成冗余)。
const int N = 1e5+10;
struct Node
{
int l,r; /// 区间端点
int ma; /// 区间最大值
int cnt; /// 出现次数
}T[N<<2]; /// 线段树数组
int a[N]; /// 原始数组
void push_up(int rt)
{
T[rt].ma = T[ls].ma>T[rs].ma?T[ls].ma:T[rs].ma;
if(T[ls].ma == T[rs].ma) T[rt].cnt = T[ls].cnt + T[rs].cnt;
else T[rt].cnt = T[ls].ma>T[rs].ma?T[ls].cnt:T[rs].cnt;
}
/*
* pair<int,int>
* first 最大值
* second 最大值的次数
*/
pair<int,int> combine(pair<int,int> x,pair<int,int> y)
{
pair<int,int> res;
if( x.first == y.first ) res = {x.first , x.second + y.second};
else res = x.first>y.first?x:y;
return res;
}
pair<int,int> range_query(int rt,int l,int r)
{
if( l <= L && r >= R ) return {T[rt].ma,T[rt].cnt}; /// 对应情况 1
pair<int,int> tema = {-0x3f3f3f3f,1}; /// 用一个很小的值来做初值
if( l <= mid ) tema = combine(tema, range_query(ls,l,r));
if( r > mid ) tema = combine(tema, range_query(rs,l,r));
return tema; /// 当两个 if 都进入了为 情况 3
}
2.11.7.3、求 最大公约数/最小公倍数
在这个问题中,我们要计算给定数组范围内所有数的最大公约数(greatest common divisor(gcd))或是最小公倍数(lowest common multiple(lcm))。
可以用完全相同的方式来解决这个问题:在树的每个顶点中存储相应顶点的GCD / LCM就足够了。合并两个顶点可以通过计算两个顶点的GCD / LCM来完成。
这里只给出两个区间合并的代码(这是最终要的),其他部分去上一个问题类似。
void push_up(int rt)
{
T[rt].gcd = __gcd(T[ls].gcd,T[rs].gcd);
T[rt].lcm = T[ls].lcm*T[rs].lcm/__gcd(T[ls].lcm,T[rs].lcm);
}
2.11.7.4、记录 \(0\) 出现的次数,并求第 \(k-th\) \(0\) 的位置
在这个问题中我们需要计算在给定区间中 数字0出现个次数,以及整个数组中第 \(k\) 个 \(0\) 出现的位置(区间内第 \(k\) 个 \(0\) 的求法将在后文出现)。
一样的,我们需要先思考线段树要存储那些值:这次我们只需存储每个区间中存储了多少个 \(0\)。其他的建树、更新和计算区间出现的 \(0\) 的次数类似于区间求和。
我们主要来解决如何求第 \(k\) 个 \(0\) 的位置。为了解决这个问题,我们要从根节点向下遍历,每次只向左或向右移动到子区间,这主要取决于第 \(k\) 个 \(0\) 在那个区间。计算到底进入那个子区间,我们只需要用到左子区间中的信息。如果左子区间中 \(0\) 的个数大于或等于 \(k\) ,那么就进入左子区间,否则进入右子区间。需要注意的是如果我们决定要进入右子区间后, \(k\) 的值需要减去左子区间含有 \(0\) 的个数。
int find_kth_zero(int rt,int k)
{
if( k > T[rt].cnt ) return -1;
if(L == R) return L;
if( T[ls].cnt >= k ) return find_kth_zero(ls,k);
else return find_kth_zero(rs,k-T[ls].cnt);
}
2.11.7.5、找到最小的大于 \(x\) 的前缀和
给定数值 \(x\) 我要尽可能快的找到最小的下标 \(i\) 满足 \(a[0,i]\) 的和大于或等于 \(x\) (\(a[]\) 中的均为非负整数)。这个问题和前一个问题的解决办法基本一致。
* 2.11.7.6、找到区间中位置最小的大于 \(x\) 的数
给定 \(x\) 以及区间 \([l,r]\) 找到区间中最小的下标 \(i\) 使得 \(a[i] > x\)。对于这个问题线段树中只用存储端点信息以及区间最大值。
我们将这个问题分成两个部分:
- 将当前处理的这个区间转移到 \([l,r]\) 的子区间中,转移时先向左移动(满足最小),如果左子区间无法满足条件或者不在 \([l,r]\) 中再进入右区间。
- 当前区间已是 \([l,r]\) 的子区间后,搜索第一个大于 \(x\) 的位置。
之前我们的搜索过程只有 \(1\) 个搜索函数,在这个例子中由于要考虑两个因素(在 \([l,r]\) 中,最小的 \(i\) 使得 \(a[i] > x\)),所以先满足一个条件,然后再切换搜索目标去满足另一个条件。
int find_first(int rt,int val)
{
if( L == R ) return L;
if( T[ls].ma > val ) return find_first(ls,val);
else return find_first(rs,val);
}
int query(int rt,int l,int r,int val)
{
if( R < l || r < L ) return -1;
if( l <= L && r >= R ){
if( T[rt].ma <= val ) return -1;
return find_first(rt,val);
}
int te = -1;
if( l <= mid ) te = query(ls,l,r,val);
if( te == -1 && r > mid ) te = query(rs,l,r,val);
return te;
}
2.11.7.7、找到一个区间的最大子区间和
在数组 \(a[0,n-1]\) 中给定 \([l,r]\) ,找到一个连续子区间 \([l',r']\) (\(l \le l'\) 且 \(r \ge r'\)) 使其和最大化。和之前一样我们还要能够进行单点修改,原始数组中的数可能为负数,最优的子区间可以为空(其和为 \(0\),这个可以特判一下,不可为空的最优子区间小于 \(0\) 则直接输出 \(0\) 就好了)。
这是线段树非常重要的一个应用。这次我们除了存储端点信息还要存储另外 \(4\) 个值分别是:整个区间和sum,包含左端点的子区间的最大和l_ma(最大前缀和),包含右端点的子区间的最大和r_ma(最大后缀和),整个区间的最大子段和ma。
如何用这些数据构建树?我们再次以递归的方式计算它:我们首先计算左子节点和右子节点的所有四个值,然后将它们组合起来以存档当前顶点的四个值。注意,当前顶点的最大子段和ma可能有三种情况:
- 左子区间的最大子段和
T[rt].ma=T[ls].ma。 - 右子区间的最大子段和
T[rt].ma=T[rs].ma。 - 左子区间的包含右端点的最大和与右子区间的包含左端点的最大和这两者的和
T[rt].ma = T[ls].r_ma + T[rs].l_ma。
因此,当前顶点的最大子段和就是这三个值的最大值。计算最大前缀/后缀和就更容易了,我们只描述最大前缀和的计算方式,后缀的计算方法与其完全类似。答案可能的情况一共有两种:
- 左子区间的最大前缀和
- 左子区间的和加上右子区间的最大前缀和。
同样,取两者的最大值就可以得到最终答案,下面是线段树定义以及合并的代码。
struct Node
{
int l,r; /// 区间端点
int sum,l_ma,r_ma,ma;
}T[N<<2]; /// 线段树数组
void push_up(int rt)
{
T[rt].sum = T[ls].sum + T[rs].sum;
T[rt].l_ma = max( T[ls].l_ma , T[ls].sum + T[rs].l_ma );
T[rt].r_ma = max( T[rs].r_ma , T[rs].sum + T[ls].r_ma );
T[rt].ma = max({ T[ls].ma, T[rs].ma , T[ls].r_ma + T[rs].l_ma });
}
建树与单点修改的代码与之前的模式基本一致,这里就不过多赘述了。现在就只剩下了查询操作,与 求最大值的同时保存其出现的次数 这一节中使用到的方式类似。为了回答这个问题,我们像以前一样沿着树向下走,将查询区间 \([l,r]\) 分解为线段树中的几个子段,并将其中的答案组合为查询的单个答案。我们还需要用到 combine 函数将查询的答案合并就像 push_up 函数一样。
Node combine(Node x,Node y)
{
Node res = {0,0,0,0,0,0};
res.sum = x.sum + y.sum;
res.l_ma = max( x.l_ma, x.sum + y.l_ma );
res.r_ma = max( y.r_ma, y.sum + x.r_ma );
res.ma = max({ x.ma, y.ma, x.r_ma + y.l_ma });
return res;
}
Node range_query(int rt,int l,int r)
{
if( l <= L && r >= R ) return T[rt];
if( l <= mid && r > mid) return combine(range_query(ls,l,r), range_query(rs,l,r) );
else if( l <= mid ) return range_query(ls,l,r);
else if( r > mid ) return range_query(rs,l,r);
}
测试题目SPOJ GSS1。
2.11.8、归并树(在节点中保存所有子数组)
这是一个独立的子部分,与其他子部分分开,因为在线段树的每个节点,我们不以压缩形式存储有关相应区间的信息(最值,区间和,···),而是存储区间的所有元素。因此,根节点将存储数组的所有元素,左子顶点将存储数组的前半部分,右顶点存储数组的后半部分,依此类推。
在该算法最简单的应用中,我们按排序顺序存储元素。在更复杂的版本中,元素不是存储在列表中,而是存储在更高级的数据结构中(set、map等)。但所有这些方法都有一个共同点,即每个顶点都需要线性内存(即与相应段的长度成正比)。
在考虑实现这种线段树时,第一个问题自然是关于内存消耗的。直觉告诉我们这种方式的存储可能是 \(\Theta(n^2)\) 的,但实际上只需要 \(\Theta(n\log_{}{n})\) 的内存。证明思路很简单,线段树的每个满节点的层次,都将把 \(a[0,n-1]\) 全部存一次,同时树的高度是 \(\log_{}{n}\) 那么总共会存 \(\Theta(n\log_{}{n})\) 个元素。
因此,尽管这种线段树看起来很奢侈,但它只比通常的线段树多消耗一点内存。下面描述了这种数据结构的几个典型应用。值得注意的是这些线段树与 2D 数据结构的相似性(实际上这是一个 2D 数据结构,但功能相当有限)。
2.11.8.1、区间内求大于或等于一个特定数的最小数值(不带修改)
给定三个数 \((l,r,x)\) 我们要找到最小位置 \(i\) ,使得 \(a[i] \ge x\) 。
在线段树的每个顶点中,我们存储相应区间中出现的所有数字的有序排列。如何尽可能有效地构建这样的线段树呢?像往常一样,我们递归地处理这个问题:让左和右子节点的有序列表构造好,再构建当前区间的有序列表。从这个角度来看,操作现在很简单,可以在线性时间内完成:我们只需要将两个排序列表组合成一个,这可以通过使用两个指针对它们进行迭代来完成(类似归并排序的方式)。c++ STL已经实现了这个算法。
merge:归并二个已排序范围[first1, last1)和[first2, last2)到始于d_first的一个已排序范围中。
由于这种线段树的结构与归并排序算法有相似之处,所以这种数据结构也常被称为归并排序树(Merge Sort Tree)。
struct Node
{
int l,r; /// 区间端点
vector<int> vec;
}T[N<<2]; /// 线段树数组
int a[N];
void build(int rt,int l,int r)
{
T[rt].l = l,T[rt].r = r;
if( l == r ){
T[rt].vec = vector<int>(1,a[l]);
return ;
} else{
build(ls,l,mid);build(rs,l,mid+1);
merge( T[ls].vec.begin(),T[ls].vec.end(),
T[rs].vec.begin(),T[rs].vec.end(), back_inserter(T[rt].vec));
}
}
我们已经知道用线段树节点来存储这种数据会花费 \(\Theta(nlog_{}{n})\) 的内存。由于归并的实现方式,他的时间复杂度也是 \(\Theta(nlog_{}{n})\) ,毕竟每个有序序列都是在线性时间内构建。
现在我们来思考如何解决询问问题,就像传统线段树一样,我们从树根沿着这棵树向下走,将 \(a[0,n-1]\) 划分为多个分段。很明显,最终的答案是每个分段的答案中数值最小的那个。
假设现在遍历到了线段树的某个顶点,我们想要计算查询的答案,即找到大于或等于给定数的最小值。由于顶点存储了区间的有序排序,我们可以简单地对该列表执行二分查找并返回第一个大于或等于的数字。
因此在树的一个段中的查询时间为 \(\Theta(log_{}{n})\) ,整个查询的时间复杂度为 \(\log^2_{}{n}\) 。
int range_query(int rt,int l,int r,int x)
{
if( l <= L && r >= R ){
auto loc = lower_bound(T[rt].vec.begin(),T[rt].vec.end(),x);
if( loc != T[rt].vec.end() ) return *loc;
else return 0x3f3f3f3f;
}
int te = 0x3f3f3f3f;
if( l <= mid ) te = min(te, range_query(ls,l,r,x));
if( r > mid ) te = min(te, range_query(rs,l,r,x));
return te;
}
0x3f3f3f3f 代表的是一个很大的数,用来表示当前区间中没有答案。
2.11.8.2、区间内求大于或等于一个特定数的最小数值(带修改)
问题描述与上小节相同,上节的解决办法有个缺陷就是如果要进行修改操作的话时间复杂度会非常高。现在我们就需要来解决这个问题,实现 \(a[i] = x\) 单点修改操作。
解决方案类似于前一个问题的解决方案,但不是在段树的每个顶点用 vector 来存储信息,而是用一个自排序的数据结构,允许快速进行搜索数字,删除数字和插入新数字等操作。由于数组可以包含重复的数字,因此最优选择是数据结构 multiset。
构造这样的线段树的方法与前面的问题基本相同,只是现在我们需要合并 multiset 以及未排序序列。这将使建树过程的时间复杂度达到 \(\Theta(n\log^2_{}{n})\) (通常合并两个红黑树可以在线性时间内完成,但是 c++ STL 不能保证这种时间复杂度)。
查询函数也几乎是一样的,只是现在应该调用 multiset 的lower_bound 函数。
最后是修改操作,为了实现做过操作,我们将从树顶向下搜索,修改每一个含有这个元素的 multiset。删除原来的元素,插入新的元素。
struct Node
{
int l,r; /// 区间端点
multiset<int> se;
}T[N<<2]; /// 线段树数组
void build(int rt,int l,int r)
{
T[rt].l = l,T[rt].r = r;
if( l == r ){
T[rt].se.insert(a[l]);
return ;
} else{
build(ls,l,mid);build(rs,l,mid+1);
merge( T[ls].se.begin(),T[ls].se.end()
,T[rs].se.begin(),T[rs].se.end()
,inserter(T[rt].se,T[rt].se.begin()) );
/// 主要这里的 inserter 的用法。
}
}
int range_query(int rt,int l,int r,int x)
{
if( l <= L && r >= R ){
auto loc = T[rt].se.lower_bound(x);
if( loc != T[rt].se.end() ) return *loc;
else return 0x3f3f3f3f;
}
int te = 0x3f3f3f3f;
if( l <= mid ) te = min(te, range_query(ls,l,r,x));
if( r > mid ) te = min(te, range_query(rs,l,r,x));
return te;
}
void single_update(int rt,int pos,int val)
{
T[rt].se.erase(T[rt].se.find(a[pos]));
T[rt].se.insert(val);
if( L == R && L == pos){
a[pos] = val;
return ;
}
if( pos <= mid ) single_update(ls,pos,val);
else single_update(rs,pos,val);
}
2.11.8.3、区间内求大于或等于一个特定数的最小数值(分散层叠优化)
和前文的问题一样,我们要找到区间内大于或等于 \(x\) 的最小值,但是这次要在 \(\Theta(\log_{}{n})\) 的时间复杂度内完成。我们将用分散层叠算法(fractional cascading)来优化时间复杂度。
分散层叠是一种简单的技术,可让缩短同时执行的多个二分查找的运行时间。我们之前的搜索方式是将任务分为多个子任务然后独立的进行各自的搜索。分散层叠技术将用单个二分搜索替代其他所有的搜索。
分散层叠最简单、直观的应用便是解决下面这个问题:给定 \(k\) 组已排序序列,我们要找到每一组中大于或等于给定数的第一个数。
我们将合并 \(k\) 个有序序列为一个大有序序列。此外我们将把每个元素 \(y\) 在所有序列中二分搜索的结果存储在一个序列中。因此,如果我们想找到大于或等于 \(x\) 的最小值,只需要执行一次二分查询,便可从索引列表中确定每个元素中的最小值。
2.11.8.4、区间第 \(k\) 小(不带修改)
核心思想:二分第 \(k\) 小的值,每次去查区间 \([l,r]\) 中小于 \(mid\) 的值,是不是刚好 \(k\) 个。
注意需要离散化不然 \([-1e9,1e9]\) 二分的话,会超时。
待修改的话就用 multiset 。
用 vector 存储的这种写法时间复杂度要高一点。
#pragma GCC optimize(2)
#include <bits/stdc++.h>
#define ls (rt<<1)
#define rs (rt<<1|1)
#define mid (T[rt].l + T[rt].r >> 1)
#define L (T[rt].l)
#define R (T[rt].r)
#define VEC (T[rt].vec)
using namespace std;
const int N = 1e5+10;
struct Node
{
int l,r;
vector<int> vec;
}T[N<<2];
vector<int> in(N);
vector<int> a(N);
void build(int rt,int l,int r)
{
T[rt] = {l,r};
if( l == r ){
T[rt].vec = vector<int>(1,a[l]);
return ;
}
build(ls,l,mid);build(rs,mid+1,r);
merge( T[ls].vec.begin(),T[ls].vec.end(),
T[rs].vec.begin(),T[rs].vec.end(), back_inserter(T[rt].vec));
}
int count_less(int rt,int l,int r,int val)
{
if( l <= L && r >= R ){
int cnt = upper_bound(VEC.begin(),VEC.end(),val ) - VEC.begin();
return cnt;
}
int res = 0;
if(l <= mid ) res += count_less(ls,l,r,val);
if(r > mid ) res += count_less(rs,l,r,val);
return res;
}
int main()
{
ios::sync_with_stdio(false);cin.tie(nullptr);
int n,m;cin >> n >> m;
for(int i = 1; i <= n ; i++) cin >> in[i];
/// 离散化
vector<int> back(in.begin(),in.end() );
sort(in.begin()+1,in.begin()+1+n);
in.erase( unique(in.begin()+1,in.begin()+1+n),in.end() );
for(int i = 1; i <= n ; i++){
a[i] = lower_bound( in.begin()+1,in.begin()+1+n,back[i] ) - in.begin();
}
build(1,1,n);
for(int i = 1; i <= m ; i++){
int x,y,k;cin >> x >> y >> k;
int l = 1, r = N;
while( l < r ){
int m = (l + r) >> 1;
if( count_less(1,x,y,m) >= k ) r = m;
else l = m + 1;
}
cout << in[l] << endl;
}
return 0;
}
2.11.9、区间更新(懒惰传播)
上面讨论的所有线段树问题都是单点更新,然而线段树允许在 \(\Theta(\log_{}{n})\) 的时间内修改整段连续的区间数值。
2.11.9.1、区间加值,单点查询
我们从一个简单的例子开始讨论:修改操作将会把 \(a[l,r]\) 区间中所有的数字加 \(x\)。第二个查询仅返回一个单点 \(a[i]\) 的值。为了高效处理修改操作,每个结点存储的是这个区间每个数增加的数。比如,执行操作 \(a[0,n-1]\) 中所有的数都加 \(3\) ,那么我们把根节点存储的值加 \(3\) 就可以了。建树的过程可以看做把叶节点都加 \(a[i]\)。通常来说我们将会把这个添加操作执行 \(\Theta(n)\) 次,但由于我们使用线段树存储区间,所以这种更新方式只用执行 \(\Theta \log_{}{n}\) 次。
我们用一个例子来说明对于数组 \(a\{2,3,5,1\}\) ,初始化之后整个线段树如下图左边所示。现在我们执行更新操作,对 \(a[0,2]\) 的所有元素都加 \(2\) ,执行完之后如右图所示。如果我们要查询 \(a[1]\) 的数值的话,那么就会把一直到 \(a[1]\) 对应的叶子节点路径上所有节点的值加起来,即 \(0+2+3=5\) 。
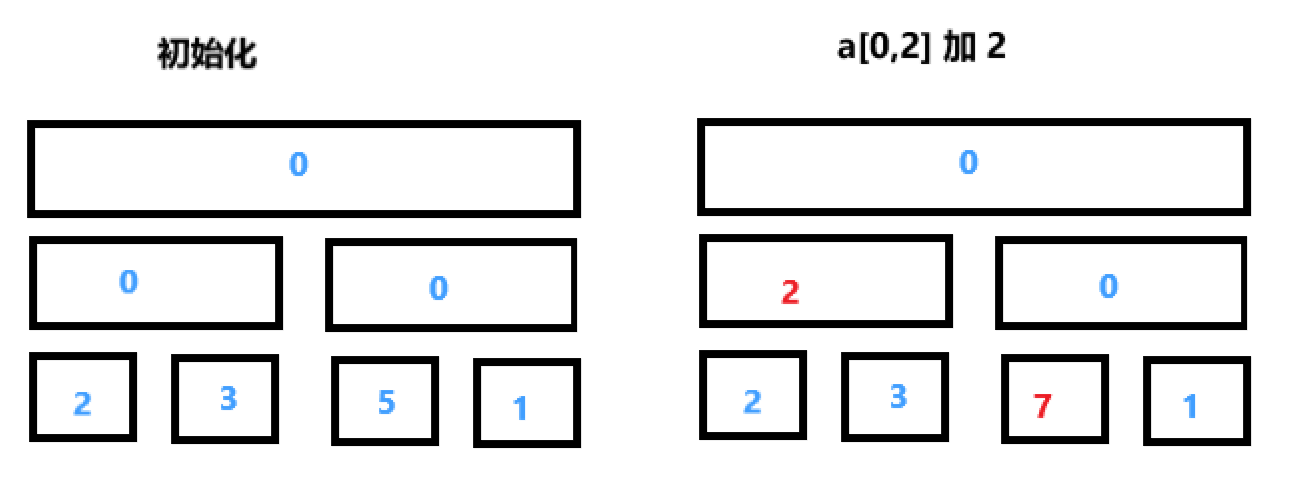
值得注意的是,这次的线段树没有合并操作。
struct Node
{
int l,r; /// 区间端点
int add;
}T[N<<2]; /// 线段树数组
int a[N];
void build(int rt,int l,int r)
{
T[rt] = {l,r,0};
if( l == r ){
T[rt].add = a[l];return ;
}else {
build(ls,l,mid);build(rs,mid+1,r);
T[rt].add = 0;
}
}
void update(int rt,int l,int r,int val)
{
if( l <= L && r >= R ){
T[rt].add += val;
return ;
}
if( l <= mid ) update(ls,l,r,val);
if( r > mid ) update(rs,l,r,val);
}
int single_query(int rt,int pos)
{
if( L == R && L == pos ) return T[rt].add;
if( pos <= mid ) return T[rt].add + single_query(ls,pos);
else return T[rt].add + single_query(rs,pos);
}
2.11.9.2、区间赋值,单点修改
现在我们要解决的问题是:把 \(a[l,r]\) 中每一个数都重新赋值为 \(p\) ,同时还要可以单点查询。
为了执行这个修改操作,我们需要在每个结点存储一个变量用以表示是否相应的区间被一个值覆盖。这就运行我们进行 懒 更新:我们只更新一些节点,让其他节点不着急更新,而不是把所有相关的节点在一次全部更新了。标记顶点意味着,相应区间的每个元素都被赋于相同的一个值。从某种意义上说,我们是懒惰的,延迟了将新值写入所有这些顶点,而只写一部分重要的节点。如果有必要,我们可以稍后再做这项乏味的工作。
例如,如果要把 \(a[0 \dots n-1]\) 的所有数字都赋为一个值,那么在线段树中实际只改变了根节点的一个数值。剩下的部分保持不变,尽管实际上这个修改应当改变树中所有节点。
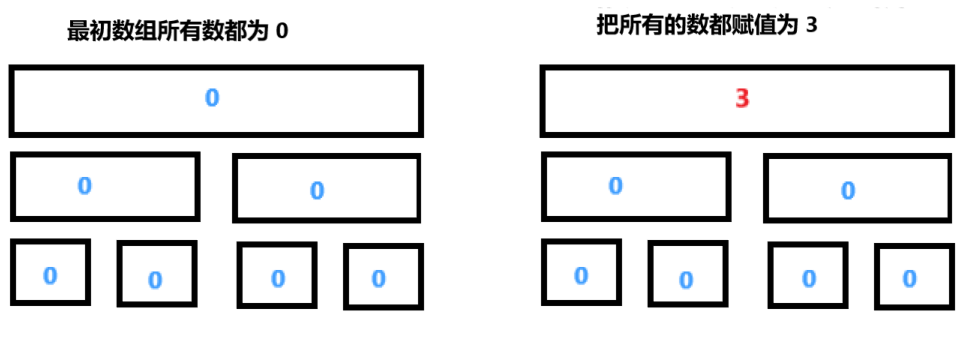
现在来处理第二个操作,将 \(a[0...n/2]\) (数组的一半)的所有数都修改为某个数。为了处理这个查询,我们必须把根节点的整个左子节点中的每个元素赋值这个数字。但在此之前,我们必须先将上次对根节点的赋值进行分发(或者说是向下传递)。这里的微妙之处在于,数组的右半部分仍然是上一次赋予的值,并且现在它没有存储任何信息。
解决这个问题的方法是将根节点的信息推送给它的子节点,也就是说,如果树的根节点被分配了一个数字,那么我们将这个数字分配给左、右子节点,并删除根节点的标记。之后,我们再把新值赋给左子节点,而不会丢失任何必要的信息。
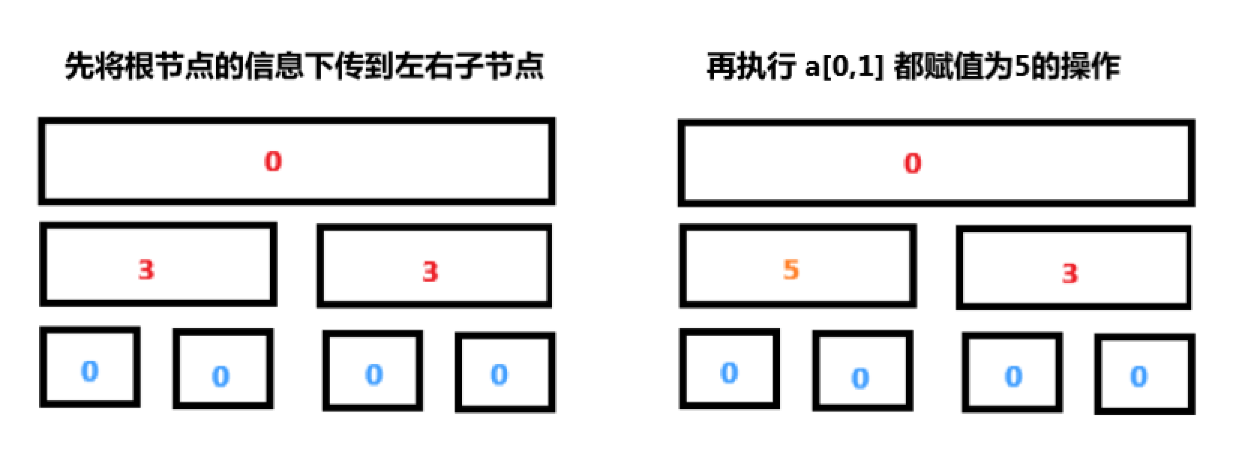
总结一下,我们得到:在树的下降过程中,对于任何操作(修改或查询),我们应该总是先将当前顶点的信息推送到它的两个子顶点。我们可以这样理解这一点,当我们从根节点下降到叶节点时,我们开始修改之前 懒得 修改的节点。在第一次修改时,我们仅仅打了一个待修改的标记,当我们再次要用到这个数据的时候(执行又一次修改或查询),我们才把数据给下传下去。懒(Lazy) 的心态是,现在如果数据还没有用到,那么我们就不着急把他向下传递,如果下面的区间开始要用到这个数据了,那么我们才把数据给他传下去,这是这一节的核心思想。 先把 \(a[l,r]\) 用最少的区间表示出来,再在这些区间上打上懒标记,这样我们才能做到不会有缺漏,同时效率也是最大化。
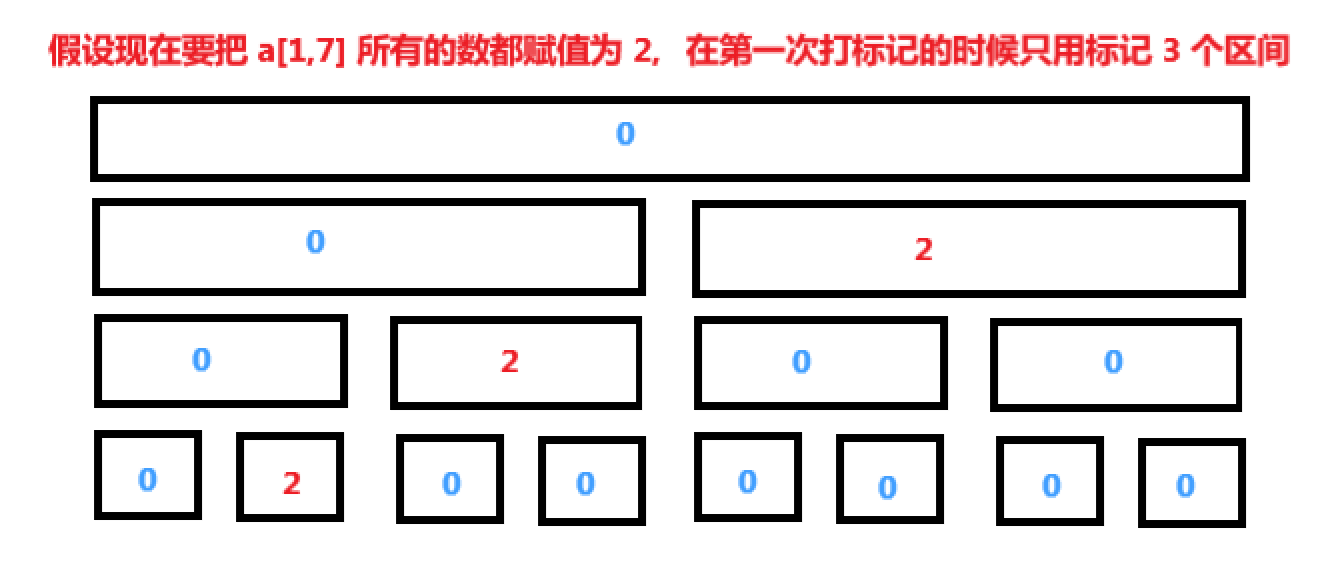
除了叶子节点之外,其他位置存储的数据都是待更新的数据,这些值最终会跟随查询操作下传到叶子节点。push_down 函数,用于下传 lazy 标记,和我们之前的 push_up 函数相反。
struct Node
{
int l,r; /// 区间端点
int data;
bool marked; /// 是否有需要下传的数据
}T[N<<2]; /// 线段树数组
int a[N];
void build(int rt,int l,int r)
{
T[rt] = {l,r,0,false};
if( l == r ){
T[rt].data = a[l];
return ;
}else {
build(ls,l,mid);build(rs,mid+1,r);
}
}
void push_down(int rt)
{
if( T[rt].marked ){
T[ls].data = T[rs].data = T[rt].data;
T[rt].marked = false;
}
}
void update(int rt,int l,int r,int val)
{
if( l <= L && r >= R ){
T[rt].data = val;
T[rt].marked = true;
return ;
}
push_down(rt);
if( l <= mid ) update(ls,l,r,val);
if( r > mid ) update(rs,l,r,val);
}
int single_query(int rt,int pos)
{
if( L == R && L == pos ) return T[rt].data;
push_down(rt);
if( pos <= mid ) return single_query(ls,pos);
else return single_query(rs,pos);
}
2.11.9.2、区间加值,区间最值
新的问题是需要在一段区间中加上一个值,同时还要能够查询一段区间的最大值。
所以对于线段树的每个顶点我们必须存储对应子线段的最大值。重要的部分是如何在修改后重新计算这些值。为了解决这个问题,我们需要在单点修改的代码基础上,在线段树定义中多一个 lazy 值(不同于上一节的 marked 标记,这将会存储数值)。lazy 将会存储还未下传给子节点的值,每次向下遍历之前,我们先把当前节点没有下传的信息传递给两个子节点。在 update 与 query 两个函数中我们都会这样做。
struct Node
{
int l,r; /// 区间端点
int ma;
int lazy; /// 是有需要下传的数据
}T[N<<2]; /// 线段树数组
int a[N];
void push_up(int rt)
{
T[rt].ma = T[ls].ma>T[rs].ma?T[ls].ma:T[rs].ma;
}
void build(int rt,int l,int r)
{
T[rt] = {l,r,0,0};
if( l == r ){
T[rt].ma = a[l];
return ;
}
build(ls,l,mid);build(rs,mid+1,r);
push_up(rt);
}
void push_down(int rt)
{
if( T[rt].lazy ){
T[ls].ma += T[rt].lazy; T[rs].ma += T[rt].lazy;
T[ls].lazy += T[rt].lazy;T[rs].lazy += T[rt].lazy;
T[rt].lazy = 0;
}
}
void range_update(int rt,int l,int r,int val)
{
if( l <= L && r >= R ){
T[rt].ma += val;
T[rt].lazy = val;
return ;
}
push_down(rt);
if( l <= mid ) range_update(ls,l,r,val);
if( r > mid ) range_update(rs,l,r,val);
}
int range_query(int rt,int l,int r)
{
if( l <= L && r >= R){
return T[rt].ma;
}
push_down(rt);
int ma = -0x3f3f3f3f;
if( l <= mid ) ma = max( ma, range_query(ls,l,r) );
if( r > mid ) ma = max( ma, range_query(rs,l,r) );
return ma;
}
上面描述的 懒标记 是线段树中非常重要的一个优化区间修改时间复杂度的方式,但是这种方式有他的局限性,能使用 lazy 标记需要满足两个条件:
- 区间节点的值可以通过当前
lazy标记来更新。 - 多次的
lazy标记能够快速合并。
对于不满足这两个条件的操作,比如开根(不满足第一点,对于维护区间和这个信息时),我们就需要用其他的方式来维护,下面我们会学到其他用于优化时间、空间的线段树写法。
2.11.10、扫描线
扫描线算法是线段树的一个应用,其主要用来计算二维坐标中矩形的周长、面积等。
顾名思义,扫描线算法的核心点在于理解 扫 这个动作以及 线 这个概念。
我们先从一个基础的问题入手:
求二维平面上的所有矩形(两边与坐标轴平行)覆盖的总面积(不重复计算重复覆盖的区域)。
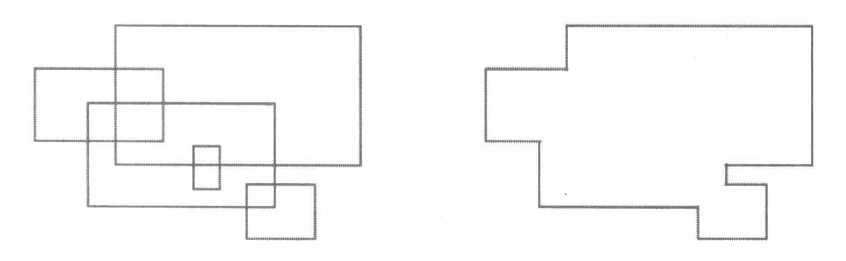
左边是数据给出的矩形,右边是我们最后要计算的面积。我们先来介绍 线 这个概念。我们把所有与 \(y\) 坐标平行的边抽离出来,同时以 \(x\) 坐标为排序标准,从小到大将这些 线 排列,如下图所示。由于我们一共有 \(n\) 个矩形,那么就会有 \(2n\) 条与 \(y\) 轴平行的边。 扫 的过程,就是从左到右依次遍历这些与 \(y\) 轴平行的边。这就是扫描线算法的核心思想。这种划分方式将所有矩形组成的区域划分为了 \(2n-1\) 个区间,之后我们只需要随着线的遍历逐一计算这些区域的面积就好了。
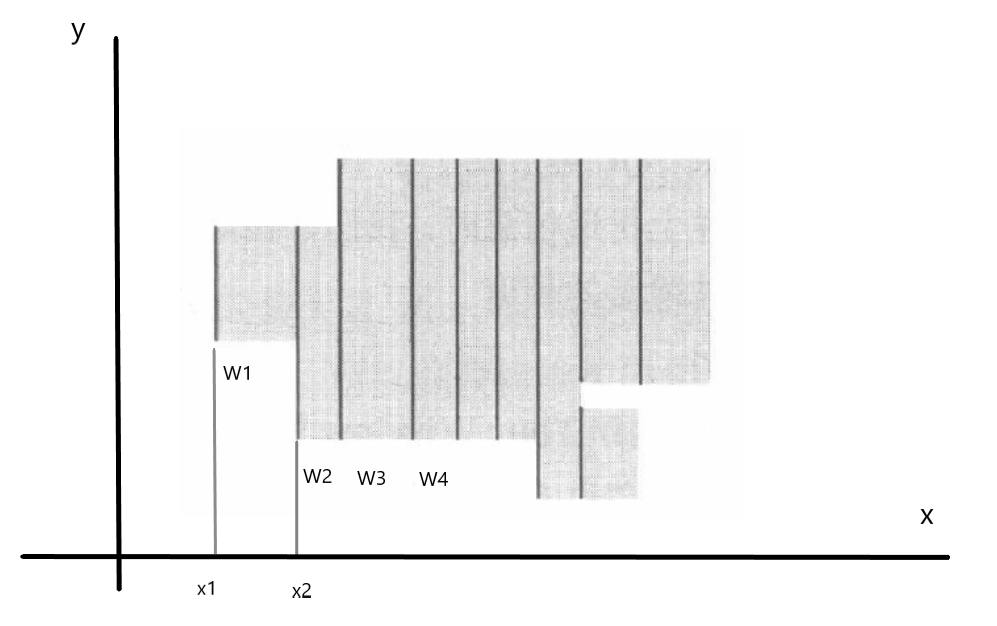
下一步就是要确定,在扫的过程中如何计算整个区域的面积。
对于每条竖边,都有一个唯一的横坐标,两条相邻竖边的横坐标之差我们记为 \(W_i\) ,即\(W_i = x_{i+1} - x_{i}\)。对于每个划分区间来说 \(W_i\) 总是易得的,而它的高即 \(H_i\) 就没那么容易计算了。我们采用一种策略,对于输入的矩形竖边中,左边的一条我们给与一个权值 \(+1\) ,右边的一条给予权值 \(-1\) ,如下图。
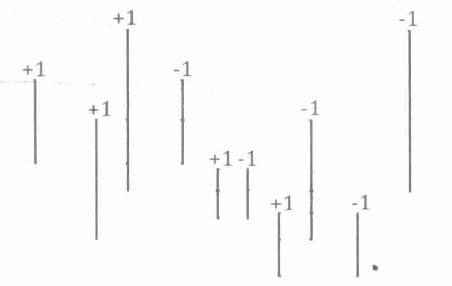
为了方便说明,我们先假设矩形的 \(4\) 个顶点坐标均为整数,对于 \(y\) 轴,我们用一个数组 \(C\) 来表示每个区域的权值(记录上图的权值)。假设第一条竖边的两个纵坐标为 \(1,3\) ,那么我们需要把 \([1,3)\) 这个区间的权值 \(+1\) 。 注意: 这个区间(\([1,3)\))的长度为 \(2\) ,\(C_1\) 表示的是 \([1,2)\) 这个区间的权值, 数组对应的不是点,而是一个长度为 \(1\) 的区间,后面的线段树中叶节点的定义同样是如此!
那么对于宽为 \(W_1\) 这个区间,我们只需要把 \(C\) 数组中所有权值为一的区间长度计算出来与 \(W_1\) 相乘,即为第一个划分区间的面积,后面的遍历过程也是这样,直至遍历到最后一条边。
可能您已经发现,这里有区间加值操作、查询整个数组中被覆盖的区间长度操作,线段树就刚好满足我们的要求。
我们用线段树来维护 \(y\) 轴的区间权值,权值大于 \(1\) 的区间就是被覆盖的区间,在从左到右扫描的过程中,我们不断更新 \(y\) 轴被覆盖的区间,遇到输入矩形的左侧边,对应的区间权值就 \(+1\) ,遇到输入矩形的右侧边,对应的区间权值就 \(-1\)。扫描完所有的竖边,那么整个划分区域的面积也就算出来了。
扫描线的思想是容易理解的,但是代码实现中有非常多重要的细节需要提高警惕。
247. 亚特兰蒂斯 - AcWing题库 我们以这个题为例题。
由于顶点坐标可能为小数,所以我们需要做离散化。还需要先对每条边以横坐标排序。
需要解释一下,如何实现的计算整个 \(y\) 轴上被覆盖的区间长度。由于争取区间加存在性质:加了之后减的一定是同一个区间。所以我们不需要将标记下传,因为不会查询到下面的区间,我们只需要整个区间的覆盖长度。所以计算一个区间的覆盖长度就出现了两种情况:
- 如果被整个覆盖的话,那么整个区间被覆盖的长度就是区间长度。
- 如果这个节点对应的区间没有被整个覆盖,那么被覆盖的区间只会是它的子区间(且这个子区间被整个覆盖),我们直接加上左右子区间被覆盖的长度就好了。
具体的实现在 push_up 中。这个函数中还有个点需要解释下 T[rt].len = dis[R+1] - dis[L] ,为什么 R+1?这个问题在之前我就解释过了,数组的一个元素代表的是一个区间,\(C_1\) 代表 \([1,2)\) ,所以这个 \(2\) 要在 \(dis_2\) 中取(因为离散化!!!)。遇到坐标不理解的地方,通常来说是没有考虑到离散化。
#include <bits/stdc++.h>
#define ls (rt<<1)
#define rs (rt<<1|1)
#define mid (T[rt].l + T[rt].r >> 1)
#define L (T[rt].l)
#define R (T[rt].r)
using namespace std;
const int N = 1e5+10;
/// 代表每条竖边
struct Vector
{
double x,y1,y2;
int k; /// 权值
bool operator < (const Vector a) const {
return x < a.x;
}
}vec[N<<1];
struct Node
{
int l,r;
int cnt; /// 完全覆盖这个区间的次数
double len; /// 区间中被覆盖的长度
}T[N<<3];/// *8 的原因是每个矩形有 2 个纵坐标,所以还要多 * 2
int n;
vector<double> dis; /// 离散化数组(仅存 y轴 坐标)
/// 返回离散化之后的值
inline int find(double x)
{
return lower_bound(dis.begin(),dis.end(),x) - dis.begin();
}
void push_up(int rt)
{
if( T[rt].cnt > 0 ) T[rt].len = dis[R+1] - dis[L]; /// 每个节点代表的是一个区间,下一个区间的左端点才是我们这个区间的末尾值
else if( L != R ) T[rt].len = T[ls].len + T[rs].len;
else T[rt].len = 0;
}
void build(int rt,int l,int r)
{
T[rt] = {l,r,0,0};
if( l == r )return ;
build(ls,l,mid);build(rs,mid+1,r);
}
void update(int rt,int l,int r,int val)
{
if( l <= L && r >= R ){
T[rt].cnt += val;push_up(rt); /// 这里要注意
return ;
}
if( l <= mid ) update(ls,l,r,val);
if( r > mid ) update(rs,l,r,val);
push_up(rt);
}
int main()
{
int t = 1;
while(~scanf("%d",&n)){
if( n == 0 ) break;
dis.clear();
int tot = 0;
for(int i = 0 ; i < n ; i++){
double x1,y1,x2,y2;
scanf("%lf%lf%lf%lf",&x1,&y1,&x2,&y2);
/// 扫描的竖边
vec[tot++] = {x1,y1,y2,+1};
vec[tot++] = {x2,y1,y2,-1};
dis.push_back(y1);dis.push_back(y2); /// 待离散化
}
/// 离散化
sort(dis.begin(),dis.end());
dis.erase( unique(dis.begin(),dis.end()), dis.end() );
/// 排序竖边
sort(vec,vec+tot); /// 所以最后少一条边
build(1,0,dis.size()-2);/// -1 是从 0 开始 ,还有个 -1 是因为节点代表的是区间
double area = 0;
/// 后面一个 find -1 的原因也是因为节点代表的是区间
/// 第一条边是不会计算面积的,只有第二条边才开始计算面积
update(1,find(vec[0].y1),find(vec[0].y2)-1,vec[0].k);
for(int i = 1; i < tot ; i++)
{
area += (vec[i].x - vec[i-1].x) * T[1].len;
update(1,find(vec[i].y1),find(vec[i].y2) - 1, vec[i].k);
}
printf("Test case #%d\n", t ++ );
printf("Total explored area: %.2lf\n\n", area);
}
}
这个代码有很多实现的细节,因为用到了很多算法线段树、离散化、二分、扫描线。
Picture - HDU 1828 - Virtual Judge (vjudge.net) 周长
2.11.11、动态开点线段树
在使用线段树这一数据结构解决问题时,我们可能会遇到以下的情况:区间的范围太大如 \([1,1e9]\),直接开会爆内存,但是要存的点只有 \(1e5\) 个。
针对这种情况,动态开点线段树便应运而生了。这种线段树在一开始只会建立一个根节点,其核心思想为:要用到这个节点对应的区间信息的时候才建立相应的节点。它与传统的线段树有以下的不同:
- 树的结构不在是完全二叉树。所以取左右儿子的方式不再是
rt<<1,rt<<1|1,而是在结构体中存储儿子节点的地址。 - 树的空间会在一开始全部开上,但是树的结构不会在一开始就建立好,仅仅在根节点创建好。
build函数与之前的作用不同了,现在的build函数可以直接理解为new Node(),相当于给你一个新的节点的地址。- 在之前的每个节点中,我们会存储节点所代表的区间 \([l,r]\) (当然也有些传统线段树版本不会存),现在我们不会存了,所以在执行更新,查询等操作的时候在函数头上要多 \(2\) 个参数来表示当前区间的范围。
使用 new 方式获取新的内存,这种方式在算法竞赛中很少使用,我们一般都采用的是使用一个数组和一个指针来模拟内存分配。代码中 T[] 数组的定义方式和之前一样(因为总共需要建立的节点数是没有变的),但是树的建立方式却不同了(后面解释)。 tot 指针就相当于一个指向空闲空间的指针,它和 T[] 数组是动态开点线段树的核心。
const int N = 1e5+10;
struct Node
{
int lson,rson; /// 存储左右儿子的指针(下标模拟的指针)
int sum,lazy;
}T[N<<2];
int root, tot;
int a[N];
int build() /// 相当于 new Node()
{
tot++; /// 初始化
T[tot].lson = T[tot].rson = T[tot].lazy = T[tot].lazy = 0;
return tot;
}
// 在main 中
tot = 0;
root = build(); /// 为 root 节点分配一个"内存"
在进行查询,更新操作的时候,可能会搜索到没有创建的节点,此时我们直接创建新的节点就可以了。
下面是一个区间加值,区间查询的题目代码与以往不同的是 \(n\) 的值为 \([1,1e9]\) ,但最多进行 \(1e5\) 次操作。
#include <bits/stdc++.h>
#define ls (T[rt].lson)
#define rs (T[rt].rson)
#define mid (L+R>>1)
#define int long long
using namespace std;
const int N = 1e5+10;
struct Node
{
int lson,rson;
int sum,lazy;
}T[N<<2];
int root, tot;
int a[N];
int build()
{
tot++;
T[tot].lson = T[tot].rson = T[tot].lazy = T[tot].lazy = 0;
return tot;
}
void create(int rt)
{
if( !ls ) ls = build();
if( !rs ) rs = build();
}
void push_up(int rt)
{
T[rt].sum = T[ls].sum + T[rs].sum;
}
void push_down(int rt,int L,int R)
{
if( T[rt].lazy ){
int ll = L ,lr = mid;
int rl = mid + 1, rr = R;
T[ls].sum += T[rt].lazy * (lr - ll + 1);
T[ls].lazy += T[rt].lazy;
T[rs].sum += T[rt].lazy * (rr - rl + 1);
T[rs].lazy += T[rt].lazy;
T[rt].lazy = 0;
}
}
void range_update(int rt,int l,int r,int L,int R,int val)
{
if( l <= L && r >= R ) {
T[rt].sum += val * (R-L+1);T[rt].lazy += val;
return ;
}
create(rt);push_down(rt,L,R);
if( l <= mid ) range_update(ls,l,r,L,mid,val);
if( r > mid ) range_update(rs,l,r,mid+1,R,val);
push_up(rt);
}
int range_query(int rt,int l,int r,int L,int R)
{
if( l <= L && r >= R ) return T[rt].sum;
create(rt);push_down(rt,L,R);
int res = 0;
if( l <= mid ) res += range_query(ls,l,r,L,mid);
if( r > mid ) res += range_query(rs,l,r,mid+1,R);
return res;
}
signed main()
{
ios::sync_with_stdio(false);
cin.tie(nullptr);
int n,m;cin >> n >> m;
root = build();
for(int i = 0; i < m ; i++){
int op,x,y,z;cin >> op >>x >> y;
if( op & 1 ){
cin >> z; range_update(root,x,y,1,n,z);
} else cout << range_query(root,x,y,1,n) << endl;
}
return 0;
}
总结:
动态开点线段树是一种新的初始化、存储线段树的方式,其他方面与传统的线段树无异。动态开点是后续知识主席树的前置知识,但它并不是一个很难的知识点。
2.11.12、权值线段树
权值线段树本质上仍然是传统的线段树,唯一的特点在于,它的作用类似于桶。举个例子如果我们要存一个数组 \(a[1,1,2,3,3,4,4,4,4,5]\) ,那么对应的权值线段长这样:
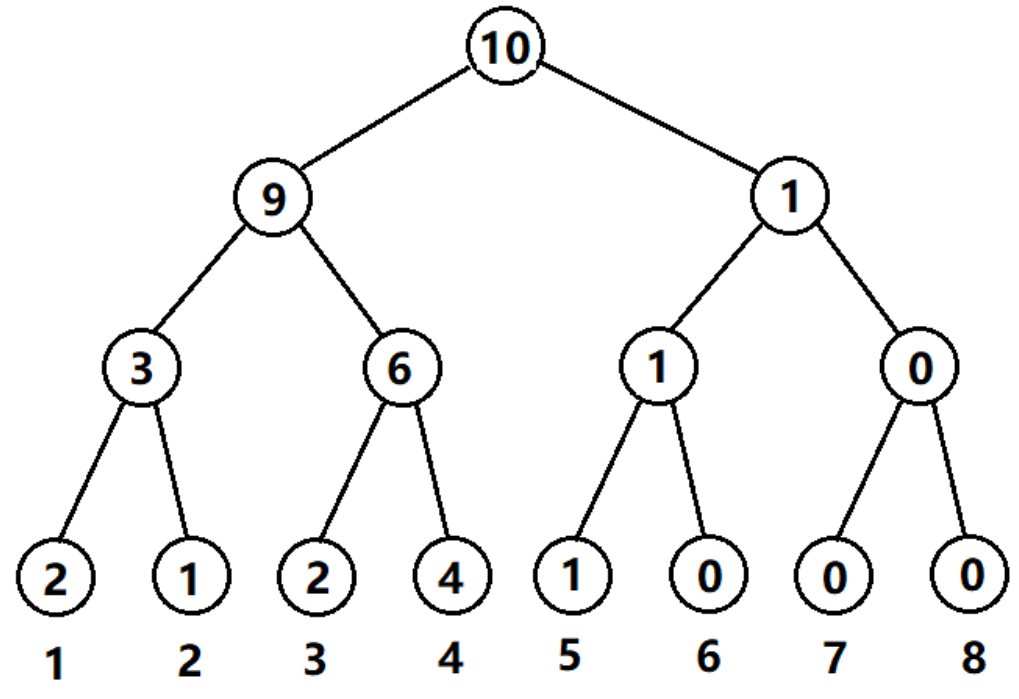
可以发现每个节点存的值为:区间下标对应的数值在整个数组中出现的次数。这个一特点使得这种线段树有非常广泛的应用,所以我们单独对这种结构的线段树进行研究,并命名为权值线段树。
再重复一次,权值线段树就是一棵普通的线段树,它的特点在于节点存储的值为区间下标对应的数值在整个数组中出现的次数。
细心的同学可能已经发现有问题了,上面一段话中有个词语特别别扭 整个数组?是的,这是权值线段树需要注意的一个事项,权值线段树中的值存的不是某个区间出现的次数,而是整个数组中数字出现的次数。也就意味着权值线段树能进行的查询操作,仅能针对整个数组进行。
这就要引出了我们权值线段树最重要的一个应用:
给定一个数组 \(a[]\) ,查询整个数组第 \(k\) 大(小)的元素的数值。P1138 第 k 小整数
我们先用用 动态开点 + 权值 的方式来写这个题。至于为什么要用这个方式来写这个题,我们先按下不表,在后面会解释。
#include <bits/stdc++.h>
#define ls (T[rt].lson)
#define rs (T[rt].rson)
#define mid (L + R >> 1)
using namespace std;
const int N = 3e5+10;
struct Node{
int lson,rson; /// 左右儿子的下标
int cnt; /// 出现了多少次
}T[N<<2];
int root,tot;
int build()
{
++tot;
T[tot].lson = T[tot].rson = T[tot].cnt = 0;
return tot;
}
void update(int &rt,int L,int R,int pos,int val)
{
if( !rt ) rt = build(); /// 如果没有这个节点就新建
if( L == R ) {
T[rt].cnt = val;return ;
}
if( pos <= mid ) update(ls,L,mid,pos,val);
else update(rs,mid+1,R,pos,val);
T[rt].cnt = T[ls].cnt + T[rs].cnt;
}
int query(int rt,int L,int R,int pos)
{
if( !rt ) return -1;/// 没有这个节点所以没有加过值,肯定没值不用新建直接返回 0
if( L == R && T[rt].cnt >= pos ) {
return L;
cout << "$" <<T[rt].cnt <<endl;
}
if( T[ls].cnt >= pos ) return query(ls,L,mid,pos);
else return query(rs,mid+1,R,pos - T[ls].cnt);
}
/// 在 [1,n] 整个数组中是否已加入这个数
bool contain(int rt,int L,int R,int val)
{
if( !rt ) return false;
if( L == R ) return T[rt].cnt>0?true:false;
if( val <= mid ) return contain(ls,L,mid,val);
else return contain(rs,mid+1,R,val);
}
int main()
{
ios::sync_with_stdio(false);
cin.tie(nullptr);
root = build();
T[0].cnt = 0;
int n,k;cin >> n >> k;
int cnt = 0;
for(int i = 0; i < n ; i++){
int te;cin >> te;
if( !contain(root,1,N,te) ) update(root,1,N,te,1),cnt++;
}
if( k <= cnt ) cout << query(root,1,N,k) << endl;
else cout << "NO RESULT" << endl;
return 0;
}
2.11.13、势能线段树
在讲势能线段之前,我们先引入势能这个概念。在物理学中势能是一个状态量,比如说重力势能,在重力势能引入后,不管一个物体按多么复杂的路线移动,最后重力势能的变化就只于高度的变化有关。这样的好处是忽略了复杂过程对计算的影响。
同样我们在这里引入势能也是一样的作用。我们来看下面这个例子
1、两个数求 \(gcd\) 的时间复杂度是 \(\Theta(\log_{}{n})\) 。
2、三个数求 \(gcd\) 的时间复杂度也是 \(\Theta(\log_{}{n})\) 。
3、\(n\) 个数求 \(gcd\) 的时间复杂度是多少呢?
直觉告诉我们,答案是 \(\Theta(n\log_{}{n})\) ,但最终的答案是 \(\Theta(n + \log_{}{n})\) 。原因在于我们每次两数求 \(gcd\) 之后的 \(ans\) ,是单调下降的,很快就会下降到 \(1\) (可能不会,如全为偶数下降到 \(2\),但只会辗转相除 \(log\) 次),那么之后的数再与 \(1\) 求 \(gcd\) 的时候就直接返回了。
我们将势能的概念引入到 \(gcd\) 求计算时间复杂度的例子中,这里的势能就是最初 \(gcd\) 的值,这个值(势能)只会单调的下降,他只会减少 \(log\) 次(基于最初的势能)。所以我们可以每次区间修改都直接下降到单点,因为这样的次数并不会太多(如果没有区间加值让它的势能又升上去的话)。
对于像区间开根号、区间 \(gcd\)、区间平方这样的区间操作来说,其对每个结点的修改量是在一定程度上是由叶结点现有的值来决定的,那么就很难实现 lazy 的合并和对区间值的直接更新,可能只有对所有叶结点进行单点修改这一种办法,而这种方法在时间开销上是绝对不允许的。
但是我们观察某些无法合并的操作如区间开根号,每个顶点最多开 \(log\) 次就会变为 \(1\) ,以后的操作都不会对这个数产生影响了。我们发现对于某些无法合并的区间操作,有着一个 最大操作次数 ,就像一个固定的势能一样,如果超过了这个势能那么之后的操作都没用了。而当连续的一段区间都势能都达到 上限 时,我们就可以像 lazy 标记一样,直接跳过这一区间。一般来说这种操作的下降是非常快的,所以均摊的时间复杂度和使用懒标记技术时花费的时间复杂度是差不多的。
我们来分析下不带修改的 区间开根号 操作的时间复杂度:
在 \(1e9\) 内的数最多开 \(6\) 次方,就会变为 \(1\)。如果 \(1 \to n\) 所有的数都开一次方,要修改 \(4n\) 个结点(也就是线段树所有的节点)。在这两个前提下,我们就可以知道,把 \(1 \to n\) 所有的数都变为 \(1\) 所要修改的次数为 \(4n \times 6\) 也就是 \(\Theta(24n)\) 的时间复杂度,这和 \(\Theta(n\log_{}{n})\) 在 \(n==1e5\) 时是同级的时间复杂度。在开完了之后对于节点的一次访问就变成了 \(\Theta(\log_{}{n})\) 了,所以总的时间复杂度为 \(\Theta(24n +n \log_{}{n})\) ,近似为 \(\Theta(n \log_{}{n})\)
所以,我们可以这样构建和操作这个线段树:
- 在每个线段树结点加入一个
势能函数,来记录和维护当前区间结点的势能情况。 - 对于每次的区间修改,若当前区间内所有结点的势能皆已为零,直接退出递归不再修改
- 若当前区间内还存在势能不为零的结点,则继续向下递归,暴力修改要求区间内每一个势能不为零的结点
总结一下,势能树的修改模式有两种情况,满势的区间我们直接跳过,没有满势的区间我们递归到叶子。势能树的势能不一定就是达到某个值,可能是区间的维护的信息满足某种条件。如果能证明,需要递归到叶子的节点能够很快的满势,之后到了区间直接返回,那么这个时候我们就可以使用势能线段树来解决这道题了。
势能线段树是非常灵活题目,主要的难点在于势能分析上面,这很多时候会要用到维护的信息的某些性质来解决问题。
2.11.14、可持续化线段树
可持久化数据结构(Perisitent data structure)表示的是一类,保存历史修改版本的数据结构。比如说我们在某个位置加了很多次值之后,想要知道没加之前的数组是什么样子的,就要用到可持久化数据结构。
可持久化线段树就是这样的能够同时维护所有的历史版本。
2.11.14.1、单点修改
2.11.15、线段树合并
2.11.x、习题
Codeforces - Xenia and Bit Operations 单点修改,单点查询
#include <bits/stdc++.h>
#define ls (rt<<1)
#define rs (rt<<1|1)
#define L (T[rt].l)
#define R (T[rt].r)
#define mid ((T[rt].l + T[rt].r) >> 1)
using namespace std;
const int N = 3e5+10;
struct Node
{
int l,r; /// 区间端点
int data;
}T[N<<2]; /// 线段树数组
int a[N];
int n,m;
void push_up(int rt)
{
if( (((int)log2(rt))&1) == (n&1) ){ // xor
T[rt].data = T[ls].data^T[rs].data;
} else { // or
T[rt].data = T[ls].data|T[rs].data;
}
}
void build(int rt,int l,int r)
{
T[rt] = {l,r,0};
if(l == r){
T[rt].data = a[l];return ;
}
build(ls,l,mid);build(rs,mid+1,r);
push_up(rt);
}
void update(int rt,int pos,int val)
{
if( L == R && L == pos ){
T[rt].data = val;return ;
}
if( pos <= mid ) update(ls,pos,val);
else update(rs,pos,val);
push_up(rt);
}
int main()
{
ios::sync_with_stdio(false);
cin.tie(nullptr);
cin >> n >> m;
for(int i = 1; i <= (1<<n) ; i++){
cin >> a[i];
}
build(1,1,(1<<n));
for(int i = 1; i <= m ; i++){
int pos,val;cin >> pos >> val;
int las = a[pos];
update(1,pos,val);
cout << T[1].data << endl;
}
return 0;
}
Codeforces - Distinct Characters Queries 区间查询,单点更新
#include <bits/stdc++.h>
#define ls (rt<<1)
#define rs (rt<<1|1)
#define L (T[rt].l)
#define R (T[rt].r)
#define mid ((T[rt].l + T[rt].r) >> 1)
using namespace std;
const int N = 1e5+10;
struct Node
{
int l,r; /// 区间端点
vector<bool> vec;
}T[N<<2]; /// 线段树数组
string c;
int n,m;
void push_up(int rt)
{
for(int i = 0; i < 26 ; i++){
T[rt].vec[i] = T[ls].vec[i] | T[rs].vec[i];
}
}
void build(int rt,int l,int r)
{
T[rt] = {l,r,vector<bool>(26,false)};
if( l == r ){
T[rt].vec[ (int)(c[l-1]-'a')] = true;
return ;
} else {
build(ls,l,mid);build(rs,mid+1,r);
push_up(rt);
}
}
void update(int rt,int pos,char val)
{
if( L == R && pos == L ){
T[rt].vec[ (int)(c[pos-1]-'a') ] = false;
T[rt].vec[ (int)(val-'a') ] = true;
c[pos-1] = val;return ;
}
if( pos <= mid ) update(ls,pos,val);
else update(rs,pos,val);
push_up(rt);
}
void combine(vector<bool> &x,vector<bool> y)
{
for(int i = 0 ; i < 26 ; i++) x[i] = x[i] | y[i];
}
vector<bool> query(int rt,int l,int r)
{
if( l <= L && r >= R ) return T[rt].vec;
vector<bool> te(26,false);
if(l <= mid) combine(te, query(ls,l,r));
if(r > mid) combine(te,query(rs,l,r));
return te;
}
int main()
{
ios::sync_with_stdio(false);
cin.tie(nullptr);
cin >> c;
int n;cin >> n;
build(1,1,c.length());
for(int i = 0; i < n ; i++){
int op;int l,r,x;char y;cin >> op;
if( op == 1 ){
cin >> x >> y;update(1,x,y);
} else{
cin >> l >> r;
auto no = query(1,l,r);
int cnt = 0 ;
for(auto it : no) if( it ) cnt++;
cout << cnt << endl;
}
}
return 0;
}
#pragma GCC optimize("03")
#include <bits/stdc++.h>
#define ls (rt<<1)
#define rs (rt<<1|1)
#define L (T[rt].l)
#define R (T[rt].r)
#define mid ((T[rt].l + T[rt].r) >> 1)
#define int long long
using namespace std;
const int N = 1e5+10;
struct Node
{
int l,r;
int sum;
}T[N<<2];
int a[N];
int n,m;
inline void push_up(int rt)
{
T[rt].sum = T[ls].sum + T[rs].sum;
}
void build(int rt,int l,int r)
{
T[rt] = {l,r,0};
if( l == r ){
T[rt].sum = a[l];return;
}
build(ls,l,mid);build(rs,mid+1,r);
push_up(rt);
}
void range_update(int rt,int l,int r)
{
if( R - L + 1 == T[rt].sum ) return ;
if( L == R ) {
T[rt].sum = sqrt(T[rt].sum);
return ;
}
if( l <= mid ) range_update(ls,l,r);
if( r > mid ) range_update(rs,l,r);
push_up(rt);
}
int range_query(int rt,int l,int r)
{
if( l <= L && r >= R ) return T[rt].sum;
int te = 0;
if( l <= mid ) te += range_query(ls,l,r);
if( r > mid ) te += range_query(rs,l,r);
return te;
}
signed main()
{
int cnt = 1;
while(~scanf("%lld",&n)){
for(int i = 1; i <= n ; i++) scanf("%lld",&a[i]);
build(1,1,n);
scanf("%lld",&m);
printf("Case #%lld:\n",cnt);
cnt ++;
for(int i = 0; i < m ;i++){
int op,x,y;
scanf("%lld %lld %lld",&op,&x,&y);
if( x > y ) swap(x,y);
if( op == 0 ){
range_update(1,x,y);
} else printf("%lld\n", range_query(1,x,y) ) ;
}
printf("\n");
}
return 0;
}
Codeforces - Ant colony 区间 gcd ,区间计数
#pragma GCC optimize("03")
#include <bits/stdc++.h>
#define ls (rt<<1)
#define rs (rt<<1|1)
#define L (T[rt].l)
#define R (T[rt].r)
#define mid ((T[rt].l + T[rt].r) >> 1)
using namespace std;
const int N = 1e5+10;
struct Node
{
int l,r;
int gcd,mi,cnt;
}T[N<<2];
int a[N];
inline void push_up(int rt)
{
T[rt].gcd = __gcd(T[ls].gcd,T[rs].gcd);
T[rt].mi = min(T[ls].mi,T[rs].mi);
if( T[ls].mi == T[rs].mi ) T[rt].cnt = T[ls].cnt + T[rs].cnt;
else T[rt].cnt = (T[ls].mi==T[rt].mi)?T[ls].cnt:T[rs].cnt;
}
void build(int rt,int l,int r)
{
T[rt] = {l,r,0,0,0};
if( l == r ) {
T[rt].gcd = T[rt].mi = a[l];T[rt].cnt = 1;
return ;
}
build(ls,l,mid);build(rs,mid+1,r);
push_up(rt);
}
Node combine(Node x,Node y)
{
Node te = {0,0,0,0,0};
te.gcd = __gcd(x.gcd,y.gcd);
te.mi = min(x.mi,y.mi);
if( x.mi == y.mi ) te.cnt = x.cnt + y.cnt;
else te.cnt = (te.mi==x.mi)?x.cnt:y.cnt;
return te;
}
Node range_query(int rt,int l,int r)
{
if( l <= L && r >= R ) return T[rt];
if( l <= mid && r > mid ) return combine(range_query(ls,l,r), range_query(rs,l,r));
else if( l <= mid ) return range_query(ls,l,r);
else if( r > mid ) return range_query(rs,l,r);
}
signed main()
{
ios::sync_with_stdio(false);
cin.tie(nullptr);
int n;cin >> n;
for(int i = 1 ; i <= n ; i ++) cin >> a[i];
build(1,1,n);
int m;cin >> m;
while(m--){
int x,y;cin >> x >> y;
auto no = range_query(1,x,y);
if( no.mi == no.gcd ) cout << (y-x+1) - no.cnt <<endl;
else cout << y-x+1 << endl;
}
return 0;
}
[P3960 NOIP2017 提高组] 列队
- \(1 \to 6\) 测试点的纯暴力写法
#include <bits/stdc++.h>
using namespace std;
const int N = 1e3+10;
int a[N][N];
int main()
{
ios::sync_with_stdio(false);
cin.tie(nullptr);
int n,m,q;cin >> n >> m >> q;
for(int i = 1; i <= n; i++)for(int j = 1; j <= m ; j++) a[i][j] = (i-1)*m + j;
for(int i = 1; i <= q; i++){
int x,y;cin >> x >> y;
int te = a[x][y];
cout << te << endl;
for(int j = y; j < m ; j++) a[x][j] = a[x][j+1];
for(int j = x; j < n ; j++) a[j][m] = a[j+1][m];
a[n][m] = te;
}
return 0;
}


 浙公网安备 33010602011771号
浙公网安备 33010602011771号