Hoppz板子
Hoppz板子_2022
前言:
还是那句话,我真的好菜
原来的算法笔记太凌乱,同时格式也不统一,不方便阅读,很多东西也没有写到点子上,在看了《算法竞赛进阶指南》之后,着实相见恨晚,这版笔记中很多叙述取自于此书。
2022_01_04
1、C++ & STL
在标题后有 * 的建议看完后面的再回来阅读。
1.1、常用库函数
1.1.1、万能头
#include <bits/stdc++.h>
原理就是套娃。我自己写的一个万能头。
// C
#ifndef _GLIBCXX_NO_ASSERT
#include <cassert>
#endif
#include <cctype>
#include <cerrno>
#include <cfloat>
#include <ciso646>
#include <climits>
#include <clocale>
#include <cmath>
#include <csetjmp>
#include <csignal>
#include <cstdarg>
#include <cstddef>
#include <cstdio>
#include <cstdlib>
#include <cstring>
#include <ctime>
#if __cplusplus >= 201103L
#include <ccomplex>
#include <cfenv>
#include <cinttypes>
#include <cstdalign>
#include <cstdbool>
#include <cstdint>
#include <ctgmath>
#include <cwchar>
#include <cwctype>
#endif
// C++
#include <algorithm>
#include <bitset>
#include <complex>
#include <deque>
#include <exception>
#include <fstream>
#include <functional>
#include <iomanip>
#include <ios>
#include <iosfwd>
#include <iostream>
#include <istream>
#include <iterator>
#include <limits>
#include <list>
#include <locale>
#include <map>
#include <memory>
#include <new>
#include <numeric>
#include <ostream>
#include <queue>
#include <set>
#include <sstream>
#include <stack>
#include <stdexcept>
#include <streambuf>
#include <string>
#include <typeinfo>
#include <utility>
#include <valarray>
#include <vector>
#if __cplusplus >= 201103L
#include <array>
#include <atomic>
#include <chrono>
#include <condition_variable>
#include <forward_list>
#include <future>
#include <initializer_list>
#include <mutex>
#include <random>
#include <ratio>
#include <regex>
#include <scoped_allocator>
#include <system_error>
#include <thread>
#include <tuple>
#include <typeindex>
#include <type_traits>
#include <unordered_map>
#include <unordered_set>
#endif
这个是他的位置

因为 Visual Studio 的 C++库中没有声明这个头文件。所以我就直接弄了一个。他的作用就是帮你写你常用的头文件,你就不用写这么多了,但是一定要清楚那个函数在那个库里面!!! 因为万一比赛的时候不支持头文件,那不是只有摆烂吗。
1.1.2、数据类型的简写
typedef long long ll;
typedef pair<int,int> pir;
ll a;
pir b;
1.1.3、关于宏
1.1.3.1、define
无参宏
在宏定义中没有参数
#define inf 0x3f3f3f3f
#define L T[rt].l
#define Mid ((T[rt].l +T[rt].r)>>1)
无参宏更像一种占位替换,他相当于直接把原来代码中的宏部分直接替换成后面的东西,仅作为字符串存储,并不会计算出他的结果。
#define N 2+2
int main()
{
int a=N*N;
printf("%d",a);
}
以我们的想法,输出的应该是 16,但是我们得到的是 8。他的计算逻辑是
直接把 N 替换到N*N 中。
所以在一些数值计算的时候一定记得加括号,同时在define语句的最后没有分号!!!
有参宏(宏函数)
C++语言允许宏带有参数。在宏定义中的参数称为形式参数,在宏调用中的参数称为实际参数。
对带参数的宏,在调用中,不仅要宏展开,而且要用实参去代换形参(有点类似printf 中的占位符)。
#define max(x,y) (x)>(y)?(x):(y); /// 实现 max 函数
值得注意的是,如果我们写一个函数形式的 max 函数是这样的:
int Max(int x, int y){return x > y ? x : y;}
区别在于,没有写变量类型!
所以这样的用法严格来说是不安全的,所以也仅仅只是我们比赛中可以这样写,但是项目中基本上不会这样写,更多的是看个人的习惯,但是一定要知道宏是不安全的!所以有些文章再说不推荐比赛的时候写宏就是这个道理。但是最主要是还是个人习惯,没必要争个胜负。
更安全的写法是用 template 后面不会扩展这个知识点,感兴趣的可以自己下去研究。
贴一个杨会的宏板子
//#pragma comment(linker,"/STACK:1024000000,1024000000")
//#pragma GCC optimize(2)
//#pragma GCC target ("sse4")
#include<bits/stdc++.h>
//typedef long long ll;
#define ull unsigned long long
//#define int __int128
#define int long long
#define F first
#define S second
#define endl "\n"//<<flush
#define eps 1e-6
#define base 131
#define lowbit(x) (x&(-x))
#define db double
#define PI acos(-1.0)
#define inf 0x3f3f3f3f
#define MAXN 0x7fffffff
#define INF 0x3f3f3f3f3f3f3f3f
#define _for(i, x, y) for (int i = x; i <= y; i++)
#define for_(i, x, y) for (int i = x; i >= y; i--)
#define ferma(a,b) pow(a%b,b-2)
#define mod(x) (x%mod+mod)%mod
#define pb push_back
#define decimal(x) cout << fixed << setprecision(x);
#define all(x) x.begin(),x.end()
#define rall(x) x.rbegin(),x.rend()
#define memset(a,b) memset(a,b,sizeof(a));
#define IOS ios::sync_with_stdio(false);cin.tie(0);
using namespace std;
#ifndef ONLINE_JUDGE
#include "local.h"
#endif
template<typename T> inline T fetch(){T ret;cin >> ret;return ret;}
template<typename T> inline vector<T> fetch_vec(int sz){vector<T> ret(sz);for(auto& it: ret)cin >> it;return ret;}
template<typename T> inline void makeUnique(vector<T>& v){sort(v.begin(), v.end());v.erase(unique(v.begin(), v.end()), v.end());}
template<typename T> inline T max_(T a,T b){if(a>b)return a;return b;}
template<typename T> inline T min_(T a,T b){if(a<b)return a;return b;}
void file()
{
#ifdef ONLINE_JUDGE
#else
freopen("D:/LSNU/codeforces/duipai/data.txt","r",stdin);
freopen("D:/LSNU/codeforces/duipai/WA.txt","w",stdout);
#endif
}
void Match()
{
#ifdef ONLINE_JUDGE
#else
Debug::Compare();
#endif // ONLINE_JUDGE
}
signed main()
{
IOS;
file();
}
Match();
return 0;
}
1.1.3.2、const
一般与数值有关的,我个人更加习惯用 const 来定义,这样数据的类型就得到了保障也更加安全。
const double eps = 1e-18; /// 表示 0.000000000000000001 区别 1e18
const int N = 1e5 + 10; /// 表示 100010 = 100000 + 10
const int maxp = 10;
const double pi = acos(-1); /// 表示圆周率
const double inf = 1e14; /// 1 后面跟上 14 个 0
同时在定义数组大小的时候,必须是 const 类型的数据才可以定义为数组的大小,常用形式为:
const int N = 2e5+10;
int a[N];
为什么+10?访问了未分配内存的空间!!!
在遍历的时候,或者计算的时候有的时候因为边界没有考虑完备,会遍历到没有定义的空间,所以为了更好的容错率一般多定义一点点。溢出的话,会报 Runtime Error 也就是直接卡死在那里,我遇到的 Runtion Error \(99\%\) 的情况都是数组越界。比如说
#include <bits/stdc++.h>
using namespace std;
vector<int> vec(100);
int main()
{
cout << vec[100] << endl;
return 0;
}
这里就访问了没有分配的内存。
1.1.3、输入,输出函数
在 c语言 中我们一般用 scanf 来输入, printf 来输出,我们会引入 <stdio.h> 这个头文件。
在 C++ 中我们一样可以用这两个来进行输入以及输出,但是我们更常用的是 cin 以及 cout 采用流式输出输出,需要引入 <iostream>。
输入
int a;
cin >>a;
输出
cout <<a <<endl;
cout << a << "\n"; // 与上面的功能相同
>> 叫做输入重定向,<<叫做输出重定向。endl 和 "\n"是一样的。
格式化输出
在 C语言 中我们可以用 %.10lf 来控制输出的精度,cout 的格式化输出较为麻烦一点
///非科学计数法输出
cout.setf(ios::fixed);
///设置输出小数点
cout << setprecision(4) << x <<endl;
一般遇到与精度有关的题的时候,我一般习惯不用流式输入输出,直接用标准输入输出。
1.1.4、与数学有关的库函数
1.1.4.1、max 与 min
虽然只是一个简单的比较大小但是都有非常非常多的写法,上述的宏定义,就不说了。
在 C++中我们可以直接用 <cmath> 库中的 max,min 函数。
#include <cmath>
#include <iostream>
using namespace std;
int main()
{
cout << max(1, 2) << endl;
return 0;
}
但是一般我们都直接用三目运算,a>b?a:b,或者写成内联函数的形式
inline int Max(int a, int b) { return a > b ? a : b; }
int main()
{
int a = 1, b = 2;
cout << Max(1, b) << endl;
// cout << (a > b ? a : b) << endl;
return 0;
}
内联函数会在编译的时候,在内联函数中的代码内嵌到原位置中,这样就可以提升运行的速度。
如果要比赛大小的数大于2怎么办?
在C++11中,支持使用大括号把要取大小的数都框起来,类似初始化数组的形式。
int ma = max({1,2,3,4,5,6})
如果我是要取得一个数组中的最大值和最小值呢?
1.1.4.2、max_element 与 min_element
要使用这两个函数,要引入 <algorithm>这个库,这两个函数的作用就是返回一个指向数组中的最大值或最小值的指针或迭代器,使用 * 取到地址、迭代器所对应的值。
int a[]={1,9,2,3,4};
int te = *max_element(a,a+5);
cout << te <<endl;
注意:诸如后面的
sort,lower_bound,这种对 \(l,r\) 区间进行操作的,都是在左闭右开 \([l,r)\) 的区间中进行操作,比如 $(a,a+5) $ 实际上是 \((a+0,a+5)\),我们知道在 C 语言中是从 \(0\) 开始的的,所以在有 \(5\) 个数字的数组中,最大下标是 \(4\),虽然是写的 \([0,5)\) 但是实际操作了的是 \([0,4]\) 。
1.1.4.3、pow 与 sqrt
首先,不要用 pow!!! 不要用 pow!!! 不要用 pow !!! 因为精度有问题。
pow(a,b)是用来求 a 的 b 次方等于多少,在校范围中,精度还是准确的,但是稍微打一点点,不会爆double,long long 他就不准确了,卡了整个集训队1个小时的教训。
这种误差在不同的C++标准中,可能不同,比如 CodeBlocks 采用的C++标准就会出现,但是Visual Studio 与 Visual Studio Code 都不会出现(这两不是同一个软件!!!)。
综上,自己手写个pow。
sqrt(a) 是用来一个数开二次方的结果,也就是取根号。
根据不用的数据类型可以选用:
- sqrt
- sqrtf
- sqrtl


关于精度
printf("%.30lf\n", sqrtl(2));
printf("%.30lf\n", sqrtf(2));
1.1.4.4 其他数学函数
/// 1、 三角函数
double sin(double); // 正弦
double cos(double); // 余弦
double tan(double); // 正切
/// 2 、反三角函数
double asin(double); // 结果介于[-PI / 2, PI / 2]
double acos(double); // 结果介于[0, PI]
double atan(double); // 反正切(主值),结果介于[-PI / 2, PI / 2]
double atan2(double, double); // 反正切(整圆值),结果介于[-PI, PI]
/// 3 、双曲三角函数
double sinh(double);
double cosh(double);
double tanh(double);
/// 4 、指数与对数
double frexp(double value, int* exp); // 这是一个将value值拆分成小数部分f和(以2为底的)指数部分exp,并返回小数部分f,即f * 2 ^ exp。其中f取值在0.5~1.0范围或者0。
double ldexp(double x, int exp); // 这个函数刚好跟上面那个frexp函数功能相反,它的返回值是x * 2 ^ exp
double modf(double value, double* iptr); // 拆分value值,返回它的小数部分,iptr指向整数部分。
double log(double); // 以e为底的对数
double log10(double); // 以10为底的对数
double log2(double); // 以2为底的对数
double pow(double x, double y); // 计算x的y次幂
float powf(float x, float y); // 功能与pow一致,只是输入与输出皆为浮点数
double exp(double); // 求取自然数e的幂
/// 5 、取整
double ceil(double); // 取上整,返回不比x小的最小整数
double floor(double); // 取下整,返回不比x大的最大整数,即 高斯函数[x]
/// 6 、绝对值
int abs(int i); // 求整型的绝对值
double fabs(double); // 求实型的绝对值
double cabs(struct complex znum); // 求复数的绝对值
/// 7 、标准化浮点数
double frexp(double f, int* p); // 标准化浮点数,f = x * 2 ^ p,已知f求x, p(x介于[0.5, 1])
double ldexp(double x, int p); // 与frexp相反,已知x, p求f
/// 8 、取整与取余
double modf(double, double*); // 将参数的整数部分通过指针回传,返回小数部分
double fmod(double, double); // 返回两参数相除的余数
/// 9 、其他
double hypot(double x, double y); // 已知直角三角形两个直角边长度,求斜边长度
double ldexp(double x, int exponent); // 计算x* (2的exponent次幂)
double poly(double x, int degree, double coeffs[]); // 计算多项式
1.1.5、upper_bound(),lower_bound()
只能升序使用,降序无法使用,同时返回的是指针或迭代器,需要引入<algorithm>
int a[] = { 1,2,4,4,6,7 };
int loc1 = lower_bound(a, a + 6, 3) - a;
int loc2 = lower_bound(a, a + 6, 4) - a;
int loc3 = upper_bound(a, a + 6, 3) - a;
auto loc4 = upper_bound(a, a + 6, 3);
cout << loc1 << endl;
cout << loc2 << endl;
cout << loc3 << endl;
cout << *loc4 << endl;
lower_bound(l,r,val)返回指向第一个大于等于val的元素的位置的迭代器(或指针)。upper_bound(l,r,val)返回指向第一个大于val的元素的位置的迭代器(或指针)。
我们可以用最后返回的地址,减去首地址的方式来得到这个元素的下标,或者直接用解引用运算符来获取这个地址所代表的值。
最大化最小值
->大于等于val的最小的值
int loc = *lower_bound(l,r,val);
最小化最大值
->小于等于val的最大的值
int loc = *--upper_bound(l,r,val) - a;
注意 upper_bound 前面的 -- 因为其返回的是大于 val的第一个数,所以要--
1.1.6、sort()
我们最常用的基本上就是 sort 他的作用就是排序,但是内部实现是非常复杂的,他会根据不用的数据量来采用不用的排序算法,他的期望时间复杂度是非常优秀的,需引入<algorithm>。
sort(a,a+n)默认升序sort(a,a+n,less<int>())升序sort(a,a+n,greater<int>())降序
我们也可以自己写一个排列升序的比较函数
bool cmp(int a, int b){return a > b;}
int main()
{
int a[] = { 1,2,4,4,6,7 };
sort(a, a + 6, cmp);
cout << a[0] << endl;
}
同时对于一个结构体,我们也可以安不同的标准来进行排序。
在一次考试中,我想以数学为第一排序,如果数学相同,就以语文为第二排序,如果语文相同就以英文为第三排序,排序标准是成绩高的排在前面。
struct Node { int ma; int ch; int en; //bool operator < (Node b) { // if (ma == b.ma) { // if (ch == b.ch) { // return en > b.en; // } // return ch > b.ch; // }; // return ma > b.ma; //} }; bool cmp(Node a, Node b) { if (a.ma == b.ma) { if (a.ch == b.ch) { return a.en > b.en; } return a.ch > b.ch; }; return a.ma > b.ma; } int main() { Node stu[5]; stu[0] = { 99,99,2 }; stu[1] = { 88,100,100 }; stu[2] = { 99,2,99 }; stu[3] = { 99,99,100 }; stu[4] = { 100,100,100 }; sort(stu, stu + 5,cmp); /* * 或者我们把注释的解除,直接用 * sort(stu,stu+5); * 效果是一样的 */ for (int i = 0; i < 5; i++) { cout << stu[i].ma << ' ' << stu[i].ch << ' ' << stu[i].en << endl; } }
1.1.7、unique()
首先,这个函数只能对相同元素在并邻在一块的序列进行去重。不能对相同元素七零八落地分布的一般序列进行去重,可以对一般数组进行排序后再用
unique实现去重目的即可,因为排好序的的序列里面相同元素一定存储在连续的地址块。
他的作用是把不重复的元素移到前面来,需要引入<algorithm>,比如说
\(\{1,2,2,3,5,5,6,7\}\) 在进行 unique 之后,就会变成
\(\{1,2,3,5,6,7,6,7\}\)最后返回一个指向第二个 6 的指针(假定为 p),在这个指针之后的所有元素都是不需要的,也就是说,我们的新的去重后的数组变成了 \([a,p)\) (a,p均为指针)
int a[] = { 1,2,2,3,5,5,6,7 };
unique(a, a + 8);
for (int i = 0; i < 8; i++) cout << a[i] << ' '; cout << endl;
1.1.8、memset()
需引入<cstring>这个函数的作用是把一个数组中的一个区间全部变成一个值,但是这个值只能是一个两位重复的16进制数 比如说 0x13131313,0x3f3f3f3f ,0x00000000,但是输入的时候只用输入 0x13。
memset(a,0x13,sizeof a) 第一个参数是输出需要赋值的首地址,第二个是值,第三个是需要初始化的范围,从首地址开始后面的多大的范围内。
memset(a, 0x13, sizeof a);
cout << a[0] << ' ' << 0x13131313 << ' ' << 0x13 << endl;
所以,想要赋值为 1 的话,是不行的。
memset(a, 0x1, sizeof a);
cout << a[0] << ' ' << 0x01010101 << ' ' << 0x1 << endl;
但是很多时候其实写一个 for循环就好了,这个只是有的时候比较方便,比如说 0,和 0x3f3f3f3f。
1.1.9、reverse()
需引入<algorithm> ,作用是把一个数组中的一个区间反转。
int a[] = {1,2,3};
reverse(a, a + 3);
for (int i = 0; i < 3; i++)cout << a[i] << ' '; cout << endl;
1.1.10、nth_element
求区间第 K 小数。
对于 a[9]={4,7,6,9,1,8,2,3,5};
1.1.11、is_sorted
检查区间是否有序
int a[];
if( is_sorted(a,a+n) ) cout << "YES"<<endl;
else cout << "NO" << endl;
1.2、string
1.2.1、什么是 string
string 中文名称 字符串 ,他的底层就是 char [] ,但是为了使字符串的操作更加方便,专门衍生出一个新的数据类型 string ,但是他自带了很多的方法,便于我们对字符串进行操作。
1.2.2、读入与输出 string
string s;
cin >> s; // 不能读入一行中的空格
getline(cin,s); // 能读入空格
cout <<s <<endl;
1.2.3、字典序与大小比较
我们按照 ASCII码定义字符串的大小;
字典序,就是按照字典(ASCII码)中出现的先后顺序进行排序。比如说:
"cba" 按照字典序排列后 变成 "abc"。
这个对于一个字符串内部的字典序排序,那么对于一个字符串数组,我们安装字典序排列是怎么样的呢?
对于字符串,先比较首字符,首字母小的排前面,如果首字母相同,再比较第二个字符,以此类推。
比如说: "abc","cbb","abd","cbbb" 排列后的结果为:
"abc","abd","cbb",cbbb
1.2.4、一些作用于 string 的函数
- 交换两个字符串
string a = "233", b = "322";
swap(a, b);
cout<< a << endl;
- 添加,赋值字符串
string s = "";
s += "a";
cout << s << endl;
s += "b";
cout << s << endl;
s.append("233");
cout << s << endl;
s.push_back('s'); // 注意和 append 的区别
cout << s << endl;
- 插入字符串
string s = "13";
s.insert(1, "22");
cout << s << endl;
- 删除字符串
string s = "1223";
s.erase(1,2);
cout << s << endl;
- 比较字符串的内容(字典序大小)
string a = "abc", b = "abd";
if (a > b)cout << 1;
else if (a < b) cout << 2;
else if (a == b) cout << 3;
else if (a >= b) cout << 4;
else if (a <= b) cout << 4;
else if( a.empty() ) cout << 5; // 如果字符串为空返回 true,反之 false
- 返回字符串大小(长度)
string a = "abc";
cout << a.size() << ' ' << a.length() << endl;
- 取子串
string a = "abcdef";
// 从下标 1 开始,后面 3 位
string sub = a.substr(1, 3);
cout << sub << endl;
- 搜寻某子串或字符
string a = "abcdef";
// 从下标 1 开始,后面 3 位
if (a.find("h") == string::npos) {
cout << "Not Find" << endl;
}
if (a.find("h") == -1) {
cout << "Not Find" << endl;
}
cout << a.find("cd") << endl;
找到的话,返回起始子串的起始下标,未找到返回 string::npos 其实就是 -1。
1.3、C++特性
1.3.1、解绑
ios::sync_with_stdio(false);
C++ 为了保证程序在使用了 printf 和 cout 时不发生冲突,进行了兼容性处理。cin、cout之所以效率低,就是因为先把要输出的东西存入缓冲区,再输出,导致效率降低。因此,很多人都会选择使用 scanf 和 printf 以加快运行速度。如果我们不同时使用这两种输出方法的话,为了提高运行速度,我们可以将其解除绑定,这样做了之后就不能同时混用cout 和 printf。
cin.tie(0);cout.tie(0);
同时,C++ 在默认的情况下 cin 与 cout 也是绑定的,每次执行 << 操作符的时候都要调用 flush,这样会增加 I/O 负担。可以通过tie(0)(0表示NULL)来解除 cin 与 cout 的绑定,进一步加快执行效率。
切记,解绑后不要在使用 scanf 和 printf 函数 !!!
1.3.2、auto 数据类型*
这个东西可以自动的把定义变量变成赋值变量的类型。这里我们用<typeinfo>来帮助我们输出数据的类型。
#include <typeinfo>
#include <bits/stdc++.h>
using namespace std;
int main()
{
auto te = 3.1415926;
cout << typeid(te).name() << endl;
return 0;
}
这样有很多很多的好处,比如说后面我们要学的STL容器 中的迭代器,每个容器的迭代器,要写很长,我们直接一个 auto 就可以搞定,比如说:
#include <typeinfo>
#include <bits/stdc++.h>
using namespace std;
int main()
{
vector<int> vec;
vec.push_back(1);
vector<int>::iterator it = vec.begin();
cout << *it << endl;
/// 对比
auto itt = vec.begin();
cout << *itt << endl;
cout << typeid(it).name() << endl;
cout << typeid(itt).name() << endl;
return 0;
}
还有就是我们后面在学队列的时候也会常用
queue<pair<int, int>> que;
while (!que.empty()) {
auto no = que.front();
que.pop();
...
}
这样也更加快捷,但是这样的话,代码的可读性会降低!!!
1.3.3、加强 for 循环*
加强 for 循环,在其他的语言中如 Java ,JavaScirpt 中叫做 forEach 当然最新的C++版本中也引入了 for_each函数。他依赖于上面的 auto 数据类型。
容器中的单变量应用
vector<int> vec(10,1);
for (auto it : vec) {
it = 3;
cout << it << endl;
}
我们运行后可以发现,这里的值输出的任然是 1。所以单一的用 auto it 来遍历是无法修改原始容器中的数据的。要使用 & 取地址符,就像在函数中传递参数一样。
vector<int> vec(10,1);
for (auto &it : vec) {
it = 3;
cout << it << endl;
}
容器中多变量的应用
map<string, int> mp;
mp["a"] = 1;
mp["b"] = 2;
for (auto it : mp) {
cout << it.first << ' ' << it.second << endl;
}
for (auto [a, b] : mp) {
cout << a << ' ' << b << endl;
}
后面的那种形式是 C++17 的新特性,如果用的C++版本低于 C++17是无法使用的!!!
1.4、C++ STL
1.4.1、什么是STL
C++标准
首先需要介绍的是 C++ 本身的版本。由于 C++ 本身只是一门语言,而不同的编译器对 C++ 的实现方法各不一致,因此需要标准化来约束编译器的实现,使得 C++ 代码在不同的编译器下表现一致。
标准模板库 STL
标准模板库(英文:Standard Template Library,缩写:STL),是一个C++软件库,大量影响了C++标准程序库但并非是其的一部分。其中包含4个组件,分别为算法、容器、函数、迭代器。
模板是C++程序设计语言中的一个重要特征,而标准模板库正是基于此特征。标准模板库使得C++编程语言在有了同Java一样强大的类库的同时,保有了更大的可扩展性。

STL 将在数据上执行的操作与要执行操作的数据分开,分别以如下概念指代:
- 容器:包含、放置数据的地方。
- 迭代器:在容器中指出一个位置、或成对使用以划定一个区域,用来限定操作所涉及到的数据范围。
- 算法:要执行的操作。
1.4.2、容器
在计算机科学中,容器以一种遵循特定访问规则的系统的方法来存储对象。
思考:我们之前的存储对象有些什么? 数组, 单个元素。


1.4.2.1、vector
std::vector 是 STL 提供的 内存连续的、可变长度 的数组(亦称列表)数据结构。能够提供线性复杂度的插入和删除,以及常数复杂度的随机访问。
-
为什么使用vector?
- vector 重写了比较运算符和赋值运算符
- vector 的可变长性
- vector的内存是动态分配的
-
vector的定义以及初始化
vector<int> a; /// 定义一个可边长度的数组,注意没有写数组大小 vector<int> a(10); /// 定义一个长度为10的可变长数组,用 () 来声明了初始化时的长度 vector<int> a(10,1); /// 定义一个长度为10 ,同时每一位的数据是 1 的数组。vector不仅仅支持定义基础数据类型的可变长数组,还可以定义自定义结构体的可变长数组。struct Node { string name; int val; }; vector<Node> vec(10,{"Hoppz",100});定义二维结构体的几种方式:
vector<int> a[10]; /// 注意区别上面 () 定义的数组 vector< vector<int> > vec(10); vector< vector<int> > arr(7,vector<int>(8,1));有几个需要注意的点:
- 第一行定义的方式是无法
-
元素访问
vector提供了如下几种方法进行元素访问at()
v.at(pos)返回容器中下标为pos的引用。如果数组越界抛出std::out_of_range类型的异常。operator[]
v[pos]返回容器中下标为pos的引用。不执行越界检查。front()
v.front()返回首元素的引用。back()
v.back()返回末尾元素的引用。data()
v.data()返回指向数组第一个元素的指针。 -
vector中的迭代器

-
与长度有关的 函数
empty()返回一个bool值,即v.begin() == v.end(),true为空,false为非空。size()返回容器长度(元素数量),即std::distance(v.begin(), v.end())。
-
元素的删除及修改
clear()清除所有元素insert()支持在某个迭代器位置插入元素、可以插入多个。复杂度与pos距离末尾长度成线性而非常数的erase()删除某个迭代器或者区间的元素,返回最后被删除的迭代器。复杂度与insert一致。push_back()在末尾插入一个元素,均摊复杂度为 常数,最坏为线性复杂度。pop_back()删除末尾元素,常数复杂度。
vector<int> vec;
vec.push_back(1);
vec.push_back(2);
vec.push_back(3);
cout << vec.size() << endl;
if (!vec.empty()) cout << "not empty" << endl;
vec.insert(vec.begin(), 2);
vec.erase(vec.begin(), vec.end() - 2);
cout << vec.front() <<endl;
1.4.2.2、deque
deque 为一个给定类型的元素进行线性处理,像 vector 一样,它能够快速地随机访问任一个元素,并且能够高效地插入和删除容器的头部以及尾部元素。但是 vector 是不可以对头部元素进行处理的。
在头部的操作与尾部一样,push_front ,pop_front,其他很多东西都很类似,就不做过多赘述了。
1.4.2.3、set
set 是关联容器,是一个自动排序,不可重复,的集合,在 搜索 、移除 和 插入 操作上拥有对数复杂度 \(nlog(n)\) 。set 内部通常采用平衡二叉树实现。平衡二叉树的特性使得 set 非常适合处理需要同时兼顾查找、插入与删除的情况。
-
插入与删除
insert(x)当容器中没有等价元素的时候,将元素 x 插入到set中。erase(x)删除值为 x 的 所有 元素,返回删除元素的个数。( 与后面的multiset 有区别)erase(pos)删除迭代器为 pos 的元素,要求迭代器必须合法。erase(first,last)删除迭代器在 范围内的所有元素。clear()清空set。
-
查询操作
count(x)返回set内键为 x 的元素数量。find(x)在set内存在键为 x 的元素时会返回该元素的迭代器,否则返回end()迭代器。lower_bound(x)返回指向首个不小于给定键的元素的迭代器。如果不存在这样 的元素,返回end()。upper_bound(x)返回指向首个大于给定键的元素的迭代器。如果不存在这样的元素,返回end()。empty()返回容器是否为空。size()返回容器内元素个数。
set<int> se;
se.insert(3);
se.insert(2);
se.insert(1);
// cout << se[0] << endl; 不支持
cout << *se.begin() << endl; /// set默认按照升序排列,所以最前面就是最小的值
cout << *(--se.end()) << endl;
for (auto it : se) { cout << it << ' '; }cout << endl;
se.erase(1);
cout << *se.begin() << endl;
// 返回的是迭代器
if (se.find(1) == se.end()) cout << "not find this key" << endl;
// 返回的是这个数的数量
if (se.count(2) != 0) cout << "find this key" << endl;

- set 在贪心中使用
在贪心算法中经常会需要出现类似 找出并删除最小的大于等于某个值的元素。这种操作能轻松地通过 set 来完成。
```c++
// 现存可用的元素
set<int> se;
// 需要大于等于的值
int x;
// 查找最小的大于等于x的元素
set<int>::iterator it = se.lower_bound(x);
if (it == se.end()) {
// 不存在这样的元素,则进行相应操作……
} else {
// 找到了这样的元素,将其从现存可用元素中移除
se.erase(it);
// 进行相应操作……
}
**例1**
> [**Hyperset - CodeForces 1287B** ](https://vjudge.net/problem/CodeForces-1287B)
>
> ---
>
> Bees Alice and Alesya gave beekeeper Polina famous card game "Set" as a Christmas present. The deck consists of cards that vary in four features across three options for each kind of feature: number of shapes, shape, shading, and color. In this game, some combinations of three cards are said to make up a *set*. For every feature — color, number, shape, and shading — the three cards must display that feature as either all the same, or pairwise different. The picture below shows how sets look.
>
> 
>
> Polina came up with a new game called "Hyperset". In her game, there are nn cards with kk features, each feature has three possible values: "S", "E", or "T". The original "Set" game can be viewed as "Hyperset" with $ k=4$.
>
> Similarly to the original game, three cards form a *set*, if all features are the same for all cards or are pairwise different. The goal of the game is to compute the number of ways to choose three cards that form a *set*.
>
> Unfortunately, winter holidays have come to an end, and it's time for Polina to go to school. Help Polina find the number of sets among the cards lying on the table.
>
> **Input**
>
> The first line of each test contains two integers nn and kk ($1≤n≤1500$, $1≤k≤30$ — number of cards and number of features.
>
> Each of the following nn lines contains a card description: a string consisting of kk letters "S", "E", "T". The ii-th character of this string decribes the ii-th feature of that card. All cards are distinct.
>
> **Output**
>
> Output a single integer — the number of ways to choose three cards that form a set.
>
> #### Examples
>
> **input**
>
> ```
> 3 3
> SET
> ETS
> TSE
> ```
>
> **output**
>
> ```
> 1
> ```
>
> **input**
>
> ```
> 3 4
> SETE
> ETSE
> TSES
> ```
>
> **output**
>
> ```
> 0
> ```
>
> **input**
>
> ```
> 5 4
> SETT
> TEST
> EEET
> ESTE
> STES
> ```
>
> **output**
>
> ```
> 2
> ```
>
> Note
>
> In the third example test, these two triples of cards are *sets*:
>
> 1. "SETT", "TEST", "EEET"
> 2. "TEST", "ESTE", "STES"
```c++
#include <bits/stdc++.h>
using namespace std;
int n,m,ans;
string s[2000];
set<string> se;
int main()
{
ios::sync_with_stdio(false);
cin.tie(0);
cout.tie(0);
cin >>n >> m;
for(int i = 0; i < n ; i++){
cin >> s[i];
se.insert(s[i]);
}
for(int i = 0 ; i < n ; i++){
for(int j = i + 1 ; j < n ; j++){
string te = "";
for(int k = 0 ; k < m; k++){
if( s[i][k] == s[j][k] ){
te += s[i][k];
}
else{
if( (int)(s[i][k] + s[j][k]) == 167 ){
te+='E';
}
else if( (int)(s[i][k] + s[j][k]) == 152 ){
te+='T';
}
else te += 'S';
}
}
if( se.find(te) != se.end()){
ans++;
//cout <<s[i] << endl <<s[j] << endl << te << endl << endl;
}
}
}
cout << ans/3 <<endl;
return 0;
}
1.4.2.4、map
-
什么是键值对


在将后者与前者结合起来就是map了

-
map
map是有序键值对容器,它的元素的键是唯一的。搜索、移除和插入操作拥有对数复杂度。map通常实现为红黑树。你可能需要存储一些键值对,例如存储学生姓名对应的分数:
Tom 0,Bob 100,Alan 100。但是由于数组下标只能为非负整数,所以无法用姓名作为下标来存储,这个时候最简单的办法就是使用 STL 中的map了! -
插入与删除操作
- 可以直接通过下标访问来进行查询或插入操作。例如
mp["Alan"]=100。 - 通过向
map中插入一个类型为pair<Key, T>的值可以达到插入元素的目的,例如mp.insert(pair<string,int>("Alan",100));或者mp.insert({key,value}) erase(key)函数会删除键为key的 所有 元素。返回值为删除元素的数量。erase(pos): 删除迭代器为 pos 的元素,要求迭代器必须合法。erase(first,last): 删除迭代器在 \([first,last)]\) 范围内的所有元素。clear()函数会清空整个容器。
下标访问中的注意事项
在利用下标访问
map中的某个元素时,如果map中不存在相应键的元素,会自动在map中插入一个新元素(一般都是用次方法插入),并将其值设置为默认值(对于整数,值为零;对于有默认构造函数的类型,会调用默认构造函数进行初始化)。当下标访问操作过于频繁时,容器中会出现大量无意义元素,影响
map的效率。因此一般情况下推荐使用find()函数来寻找特定键的元素。 - 可以直接通过下标访问来进行查询或插入操作。例如
-
查询操作
count(x): 返回容器内键为 x 的元素数量。复杂度为 (关于容器大小对数复杂度,加上匹配个数)。find(x): 若容器内存在键为 x 的元素,会返回该元素的迭代器;否则返回end()。lower_bound(x): 返回指向首个不小于给定键的元素的迭代器。upper_bound(x): 返回指向首个大于给定键的元素的迭代器。若容器内所有元素均小于或等于给定键,返回end()。empty(): 返回容器是否为空。size(): 返回容器内元素个数。
map_demo01
map<string,int> mp;
mp["Hoppz"] = 233;
mp["Gary"] = 111;
mp["qiubi"] = 222;
cout << mp["Hoppz"] << endl;
for (auto it : mp) {
cout << it.first << ' ' << it.second << endl;
}
mp["aa"] = 22;
mp["ab"] = 23;
cout << endl;
for (auto it : mp) {
cout << it.first << ' ' << it.second << endl;
}
map_demo02
map<string,int> mp;
mp["Hoppz"] = 233;
mp["Gary"] = 111;
mp["qiubi"] = 222;
if (mp["qiuqiu"] == 233) {
cout << "qiuqiu" << endl;
}
if (mp.count("qxq")) {
cout << "qxa" << endl;
}
for (auto it : mp) {
cout << it.first << ' ' << it.second << endl;
}
例2
A Dyson Sphere is a hypothetical megastructure that completely encompasses a star and captures a large percentage of its power output. The concept is a thought experiment that attempts to explain how a spacefaring civilization would meet its energy requirements once those requirements exceed what can be generated from the home planet’s resources alone. Only a tiny fraction of a star’s energy emissions reach the surface of any orbiting planet. Building structures encircling a star would enable a civilization to harvest far more energy.
One day, Moca has another idea for a thought experiment. Assume there is a special box called Dyson Box. The gravitational field in this box is unstable. The direction of the gravity inside the box can not be determined until it is opened.
The inside of the box can be formed as a 2-dimensional grid, while the bottom left corner’s coordinate is $ (0, 0)$ and the upper right corner’s coordinate is (\(2 · 10^5,2 · 10^5\) ). There will be n events. In the i-th event, a new cube will appear, whose upper right corner’s coordinate is (\(x_i , y_i\)) and bottom left corner’s coordinate is (\(x_i − 1, y_i − 1\)).
There are two directions of gravity in the box, vertical and horizontal. Suppose Moca opens the box after the i-th event. In that case, she has $ \frac{1} {2}$ probability of seeing the direction of the gravity inside the box is vertical, and the other $ \frac{1} {2}$ probability is horizontal. And then, she will measure the total length of the outline of all the cubes. If the direction of gravity is horizontal, all the cubes inside will move horizontally to the left under its influence. Similarly, vertical gravity will cause all the cubes to move downward.
Moca hates probability, so that she is asking for your help. If you have known the coordinates of all the cubes in chronological order, can you calculate the total length of these two cases after each event?
Input
The first line contains one integer n (1 ≤ n ≤ 2 · 105 ) – the number of cubes. Each of the following n lines describes a cube with two integers xi , yi (1 ≤ xi , yi ≤ 2 · 105 ). It is guaranteed that no two cubes have the same coordinates.
Output
For each of the n cubes, print one line containing two integers – two answers when the the direction of gravity is vertical and horizontal.
Note
In the only example, the inside of the box is as below, and the bold lines mark the outline of all the cubes. After the 1-st event:
1.4.2.5、pair
这里补充一个数据类型 pair ,可以把它理解为为 first ,second 两个值的一个数组,这两个值可以是不同的数据类型比如,pair<string,int>,他的实现是基于 struct 结构体的,所以我们在访问他的数据的时候不用调用方法,当然我们也可以自己写一个 struct 。
struct Node
{
string first;
int second;
};
pair<string,int> pir;
// 两者都可以
- 定义
pair<string,int> pir; /// 定义一个 first 为 string类型,second 为 int 类型的 pair
pair<string, vector<int>> /// 定义一个 first 为 string类型 ,second 为 vector<int> 数组的一个 pair
- 赋值
在C++ 11中我们可以直接用 {} 来对其进行赋值,但是如果不支持 C++11 ,不支持 {} 赋值的话,可以用 make_pair() 函数进行赋值。
pair<string,int> pir = {"Hoppz",233};
pir = make_pir("Hoppz",233);
- 调用
如果我们要调用元素的值我们可以直接用成员运算符. 来访问,大家可以理解为上面提到的,struct Node 这个结构体访问他的 first,second 变量。
pair<string,int> pir = {"Hoppz",233};
pir.first = "Gary";
pir.second = "23333";
cout << pir.fisrt << ' ' << pir.second <<endl;
- 数组
我们可以定义一个 pair 数组,就和普通的数组一样。
const int N= 2e5+10;
pair<string,int> pir[N];
1.4.3、Struct 重写 & 在 STL容器中的应用
#include <iostream>
#include <iomanip>
#include <cstdio>
#include <set>
#include <algorithm>
using namespace std;
struct Point
{
double x,y;
Point(double _x,double _y){
x = _x,y = _y;
}
bool operator < (const Point& b) const{
if( x == b.x ){
return y< b.y;
}
return x < b.x;
}
Point(){}
};
int main()
{
set<Point> se;
se.insert({3,24325});
se.insert({283,25});
se.insert({21453,2435});
se.insert({213,35});
for(auto it :se){
cout << it.x << ' ' <<it .y <<endl;
}
return 0;
}
1.4.4、关于 __int128
一般来说,我们用的最大的数据类型是 long long 他相当于一个 64位 的二进制数,在C++ 的 Linux 环境下,可以使用 __int128 a 来定义一个 128位 的二进制数。他最大可以用来表示 \(1.7e38\) ,也就是最大38位的数,而 long long 最大可以表示 \(9.2e19\)。
注意:
__int128在windows环境下无法使用,只有在Linux环境下可以使用,同时__int128的读入要单独写读入函数和快读一个原理,输出是可以用printf和cout的。#include <bits/stdc++.h> #define int __int128 using namespace std; int read() { int ans = 0, f = 1; char c = getchar(); while (!isdigit(c)) { if (c == '-')f = -1; c = getchar(); } while (isdigit(c)) { ans = ans * 10 + c - '0'; c = getchar(); } return ans * f; } signed main() { int t;t = read(); return 0; }
1.5、位运算
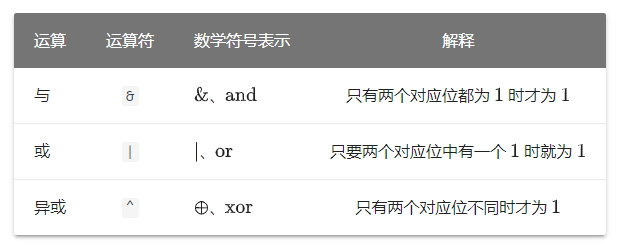
技巧

2、基础算法
2.1、快速幂
C ++底层原理(不用把数据开成 long long,如果 p 在 int 内)
在 C++ 中,两个数值执行算术运算时,以参与运算的最高数值类型基准,与保存结果的变量类型无关。换言之,虽然两个 32位整数 的乘积可能超过 int 类型的表示范围,但是 CPU 只会用 1 个 32位寄存器 保存结果,造成我们常说的越界现象。因此,我们必须把 **其中一个数强转为 64 位整数类型 long long ** 参与运算,从而得到正确的结果。最终对 p 取模以后,执行赋值操作,该结果会被隐式转换成 int 存回 ans 中。
数学原理
以求 \(5^{11}\) 为例,\(11\) 的二进制表示为 1011 ,那么
所以我们就可以迭代的求 \(5\) 的 \(2\) 的幂次方就ok了
代码
int qmi(int a, int b, int p)
{
int ans = 1 % p;
while (b) {
if (b & 1) ans = (long long)a * ans % p;
b >>= 1;
a = (long long)a * a % p;
}
return ans;
}
2.2、差分
差分的推论
如果对一个区间进行 +1 or -1 操作
- 最少的操作次数
- 最少的操作次数有多少种不同的答案
令原数组为 a \(a_1,a_2,...,a_n\),差分数组为 b
\(b[0] = a[0] ;b[n+1] = 0\)
对原序列的操作,相当于在差分数组 \(b_1,b_2,..,b_{n+1}\) 中 选出任意两个数,一个加一,一个减一。目标是把 \(b_2,b_3,...,b_n\) 全变成 \(0\) ,最终得到的数列 a 就是由 \(n\) 个 \(b_1\) 构 成。
从 \(b_1,b_2,...,b_n+1\) 中任选两个数的方法可分为四类:
- 选 \(b_i\) 和 \(b_j\) ,其中 \(2\le i,j\le n\) 。这种操作会改变 \(b_2,b_3,b_n\) 中的两个数的值。
- 选 \(b_1\) 和 $
2.3、二分
二分的基础用法...
2.3.1、整数集合上的二分
在单调序列 a 中查找 \(\ge x\) 的数中最小的一个。 最大化最小值
while (l < r) {
int mid = (l + r) >> 1;
if (a[mid] >= x) r = mid;
else l = mid + 1;
}
在单调序列 a 中查找 \(\le x\) 的数中最大的一个。最小化最大值
while (l < r) {
int mid = (l + r + 1) >> 1;
if (a[mid] <= x) l = mid;
else r = mid - 1;
}
注意
lower_bound,upper_bound与之的区别。
最小化最大值例题:
2.4、贪心
贪心是一种在每次决策时当前意义下最优策略的算法,因此,使用贪心法要求问题的整体最优策略可以由局部最优性推导出。这个非常非常非常重要
2.4.1、排序不等式
排队打水https://www.acwing.com/problem/content/description/915/
2.5、归并
2.5.1、归并排序
2.5.2、双路归并
2.5.3、多路归并
m 个序列,每个序列有 n 个数,在每个序列中只选一个数出来求和,我们可以知道一共有 \(n^m\) 种结果,输出结果中最小的 n 个数。链接
首先我们对于只有 \(2\) 个序列来说(从两个序列中各选 \(1\) 个数求和,最小的 \(n\) 个数),设第一个序列为 \(a_i\) , 第二个序列为 \(b_i\) ,我们对 \(a_i\) 序列排好序。以以下的形式构成矩阵。
\((b_1+a_1) + (b_1+a_2) + (b_1+a_3)+...+(b1+an)\)
\((b_2+a_1) + (b_2+a_2) + (b_2+a_3)+...+(b2+an)\)
\((b_3+a_1) + (b_3+a_2) + (b_3+a_3)+...+(b3+an)\)
\(...\)
\((b_n+a_1) + (b_n+a_2) + (b_n+a_3)+...+(bn+an)\)
因为 \(a_i\) 序列是有序的,那么最小的一组和,必定出现在第一列 (\(b_1+a_1\) or \(b_2+a_1\) ...),我们选出第一列中最小的值然后删去(假定为 \(b_j\)),那一列的第一个数就变成了 \((b_j+a_2)\) ,
\((b_1+a_1) + (b_1+a_2) + (b_1+a_3)+...+(b1+an)\)
\((b_2+a_1) + (b_2+a_2) + (b_2+a_3)+...+(b2+an)\)
\(...\)
\((b_j+a_2) + (b_j+a_3)+...+(bj+an)\)
\(...\)
\((b_n+a_1) + (b_n+a_2) + (b_n+a_3)+...+(bn+an)\)
此时任然满足,最小的一组和,必须出现在第一列中。所以我们就按照这样的方式就可求出以两个序列最小的 \(n\) 组和。对于 \(n\) 组序列,我们直接用 \(1,2\) 组的结果与 \(3\) 组归并,得到的结果再与第 \(4\) 组归并,以此类推,我们就求出了结果。
那么现在的问题就是如何选出第一列中最小的值然后删去,这就用堆来维护就可以了。以上。
#include <bits/stdc++.h>
using namespace std;
typedef pair<int, int> pir;
const int N = 2e3 + 10, M = 1e3 + 10;
int a[N], b[N], c[N];
int m, n;
void merger()
{
priority_queue< pir, vector<pir>,greater<pir> > pro;
for (int i = 0; i < n; i++) pro.push({a[0]+b[i],0 });
for (int i = 0; i < n; i++) {
auto no = pro.top(); pro.pop();
c[i] = no.first;
pro.push({ no.first - a[no.second] + a[no.second + 1] , no.second + 1 });
}
memcpy(a, c, sizeof c);
}
void solve()
{
cin >> m >> n;
// 先读入第一行,方便处理
for (int i = 0; i < n; i++)cin >> a[i];
sort(a, a + n);
for (int i = 1; i < m; i++) {
for (int j = 0; j < n; j++) cin >> b[j];
merger();
}
for (int i = 0; i < n; i++) {
cout << a[i] << ' ';
}cout << endl;
}
int main()
{
cin.tie(0)->sync_with_stdio(false);
int t; cin >> t;
while (t--)solve();
return 0;
}
2.x、经典问题
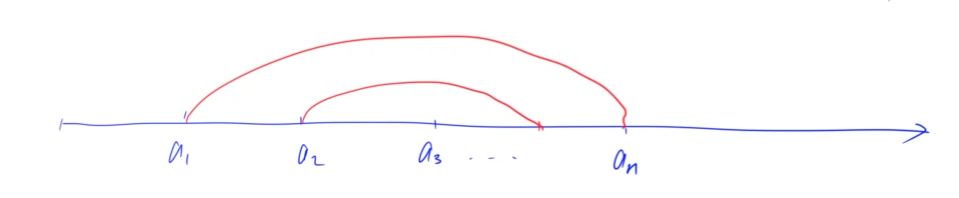
2.x.1、仓库选址
在一条数轴上有 \(N\) 家商店,它们的坐标分别为 \(A1∼AN\)。现在需要在数轴上建立一家货仓,每天清晨,从货仓到每家商店都要运送一车商品。为了提高效率,求把货仓建在何处,可以使得货仓到每家商店的距离之和最小。

相当于我们要求
由绝对值不等式我们知道 \(|x-a| + |x-b| \ge |a-b|\) ,也就是说求一个点到另外两个点的距离和最小,我们把要求的这个点放在任意,这两点之间都可以。
把这个定义拓展在多个点求一个点,我们可以采用两两配对的方式,第一个点和最后一个点配对,第二个的点和倒数第二个点配对,以此类推。
我们就可以发现在个数为奇数的情况,最中间那个数的位置就是最优解,如果是偶数的情况,中间两个数之间的任意位置都可以。
int n;
cin >> n;
vector<int> vec(n);
for (int i = 0; i < n; i++) {
cin >> vec[i];
}
sort(vec.begin(), vec.end());
int64_t s = vec[(n >> 1)],sum=0;
for (int i = 0; i < n; i++) {
sum += abs(vec[i] - s);
}
cout << sum << endl;
2.x.2、均分纸牌问题(中位数)
有 \(M\) 个人排成一行,他们手中分别有 \(C[1],C[2],...,C[M]\) 张牌,在一次操作中,可以把自己的手中的牌交给他旁边的一个人,求至少需要多少次操作,让每个人手中的纸牌数量是相等的。保证所有人的手牌数量之和能整除人数。最右边的人只能给他左边的人,最左边的人只能给他左边的人。
(题目:均分纸牌_变形)
首先我们定义
对于第一个人 \(C[1]\)
- 若 \(C[1] > ave\) ,则第一个人需要给第二人 \(C[1] - ave\) 张牌,即把 \(C[2]\) 加上 \(C[1]-ave\)。
- 若 \(C[2]<ave\) ,则第一个人需要从第二个人手里拿 \(ave - C[1]\) 张牌,即把 \(C[2]\) 减去 \(ave-C[1]\)。
对于之后的每一个人我们都按照这类方式来考虑,即使在之后的某个时刻 \(C[i]\) 变为了负数也没事。

int n,sum = 0;
cin >> n;
for (int i = 0; i < n; i++) {
cin >> c[i]; sum += c[i];
}
int ave = sum / n;
int op_num = 0;
for (int i = 0; i < n; i++) {
if (c[i] != ave) {
op_num += abs(ave - c[i]);
c[i + 1] += c[i] - ave;
}
}
cout << op_num << endl;
环形均分纸牌,所有人围成一个圈,也就是说第一个人可以给最后一个人牌,最后一个人也可以给第一个人牌。

合适取得最小值呢?
当 \(x_n\) 等于序列 \(c\) 的中位数时,该式取得最小值
#include <bits/stdc++.h>
using namespace std;
typedef long long ll;
const int N = 1e6 + 10;
ll a[N];
ll st[N];
int main()
{
ios::sync_with_stdio(false);
cin.tie(nullptr);
int n;
cin >> n;
ll sum = 0;
for(int i = 1; i <= n ; i++){
cin >> a[i]; sum += a[i];
}
ll ave = sum / n;
ll pre = 0;
for (int i = 1; i <= n; i++) {
pre += a[i];
st[i] = i * ave - pre;
}
nth_element(st + 1, st + (n >> 1)+1 , st + n+1);
ll te = st[(n >> 1) + 1],ans = 0;
for (int i = 1; i <= n; i++) {
ans += abs(te - st[i]);
}
cout << ans << endl;
return 0;
}
3、搜索
3.x、树与图的深度优先遍历
4、数论
4.1、数学技巧总结
4.1.1、分治求 \(1+p^1+p^2+...+p^c\)
-
若 c 为奇数
\[sum(p,c) = (1+p+···+ p^{\frac{c-1}{2}}) +(p^{\frac{c+1}{2}} + ···+ p^c)\\ =(1+p+···+p^{\frac{c-1}{2}}) + p^{\frac{c+1}{2}} \times(1+p+···+p^{\frac{c-1}{2}})\\ =(1+p^{\frac{c+1}{2}})\times sum(p,\frac{c-1}{2}) \] -
若 c 为偶数
\[sum(p,c) = 1 + p \times sum(p,c-1) \]
代码
4.1.2、等差,等比数列
等差数列
等比数列:
4.1.4、一些公约数公式
\(gcd(x,y) = gcd(x,y-x)\)
4.1.5、平方和
例如 \(n == 3\) 的情况
5、数据结构
5.2、树状数组 (Binary Indexed Tree)
5.2.1、树状数组概念
5.2.1.1、引入
回忆一下之前学过的差分,以及前缀和。
运用差分的知识,我们可以很快的实现区间加法,但是有个很明显的弊端就是如果我们要得到某个位置在操作完成后的值,时间复杂度是 \(O(k)\) 的,\(k\) 为这个值在数组中从前先后的位置,也就是我们要把差分数组求出他的前缀和,我们才知道他变化后具体的值为多少。
现在我们要学习的树状数组就可以很好的解决这个问题。
5.2.1.2、树状数组原理
这一小节,我们来解决对于一个数,我们如何把他划分成 \(log_n\) 个小区间,这个问题。
首先我们把任意正整数,用二进制的方式书写,以 11 为例,他的二进制表示为 1011 。
我们把一个数 \(x\) 的二进制 01 数组记为 \(A_k = \{A_{k-1},A_{k-2},...,A_{2},A_{1},A_{0}\}\) ,如果这个位置不等于 0 那么 \(A_k=2^{k}\),否则为 \(0\)。
我们再提取出所有非 0 项,表示为 \(\{A_{i_1},A_{i_2},..A_{i_m}\}\) ,同时满足 \(A_{i_1} > A_{i_2} > ... > A_{i_m}\)。进一步的,区间 \([1,x]\) 可以被分成 \(O(log_x)\) 个小区间:
-
长度为 \(A_{i_1}\) 的小区间 \([1,A_{i_1}]\)
-
长度为 \(A_{i_2}\) 的小区间 \([A_{i_1}+1,A_{i_1} +A_{i_2}]\)
-
长度为 \(A_{i_3}\) 的小区间 \([A_{i_1}+A_{i_2}+1,A_{i_1}+A_{i_2}+A_{i_3}]\)
...
对于 11 来说 \(A_k = \{8,0,2,1\}\) ,\(A_i=\{8,2,1\}\),进一步的,区间 \([1,11]\) 就可以表示为 \(\{[1,8],[9,10],[11] \}\) 这三个小区间。
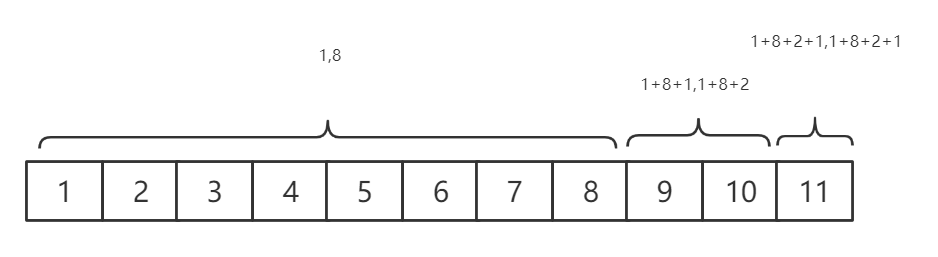
这些小区间的共同点是:若结尾为 \(R\) ,则区间长度就等于 \(R\) 的 二进制分解 下最小的 \(2\) 次幂,即 lowbit(R) ,我们还是用上面的 11 来举例 \(x = 11 = 2^3 + 2^1 + 2^0\) ,区间 [1,11] 就可以分解为 [1,8],[9,10],[11] 三个小区间,长度分别为 lowbit(8) = 8 ,lowbit(10) = 2 ,lowbit(11) = 1 。
5.2.1.3、lowbit 原理
lowbit(n) 定义为非负整数 \(n\) 在二进制表示下 最低位的 1 及其后面所以的 0 构成的数值。例如 \(n=10\) 的二进制表示为 \((1010)_2\) ,则 \(lowbit(n) = 2 = (10)_2\) 。
设 \(n>0\) ,\(n\) 的 第 \(k\) 位是 \(1\) ,第 \(0\sim k-1\) 位都是 \(0\)。
为了实现 lowbit 运算,先把 \(n\) 取反,此时第 \(k\) 位变为 \(0\),第 \(0\sim k-1\) 位都是 \(1\)。再令 \(n=n+1\),此时因为进位,第 \(k\) 位变成 \(1\) ,第\(0\sim k-1\) 位都是 \(0\)。
在上面的取反加 \(1\) 操作后, \(n\) 的第 \(k+1\) 到最高位恰好与原来取反,所以 n&(~n+1) 仅有第 \(k\) 位为 \(1\),其余位都是 \(0\)。而在补码下,~n = -1-n 因此
所以,我们就得到了 lowbit(x) = x&(-x) 这个公式。
5.2.1.4、什么是树状数组
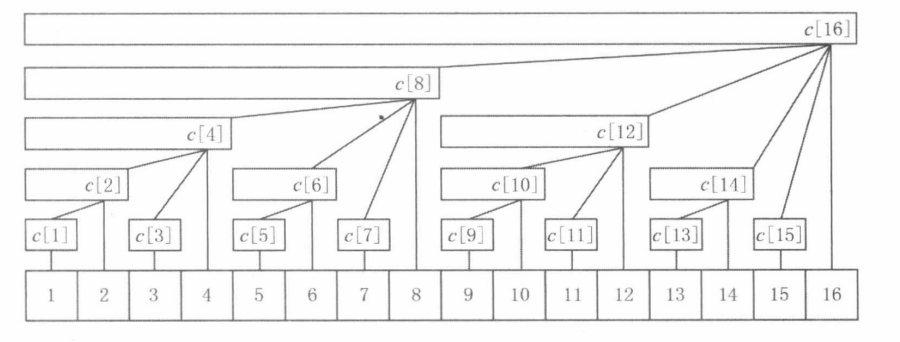
树状数组(Binary Indexed Tree,简称BIT)可以简单的理解为一个高效维护前缀和的数据结构,他的主要思想就基于上述的子区间划分。对于给定的序列 \(a\) ,我们建立一个数组 \(c\) ,其中 \(c[x]\) 保存序列 \(a\) 的区间 \([x-lowbit(x) + 1,x]\) 中所有数的和。
事实上,数组 \(c\) 可以看做一个下图所示的树形结构,最下边的一行是 \(N\) 的叶子节点 \((N=16)\) ,代表数值 \(a[1\sim N]\)。该结构满足以下性质:
-
每个内部节点 \(c[x]\) 保存以它为根的子树的中所有叶节点的和。
-
每个内部节点 \(c[x]\) 的子节点个数等于
lowbit(x)的位数。 -
除树根外,每个内部节点 \(c[x]\) 的父节点是 \(c[x+lobwbit(x)]\)
-
树的深度为 \(log_N\)
如果 \(N\) 不是 \(2\) 的整数次幂,那么树状数组是一个具有同样性质的森林结构。
5.2.2、树状数组的基本操作
我们用数组 \(c\) 来存储树状数组,每一 \(c[i]\) 表示的就是他所代表的区间的前缀和,如上图所示。
对于序列 \(a=\{1,3,9,2,3,5,1,2\}\) ,那么
5.2.2.1、单点加值
我们可以发现 \(a[1]\) 的值,会在后面的 \(a[2],a[4],a[8]\) 中都有记录,同时可以发现 \(1+lobit(1)=2\) ,\(2+lowbit(2) = 4\) , $4+lowbit(4) =8 $ ,所以我们在 \(a[x]\) 位置上加值的时候要把他后面所有包含了这个数的区间都加上 \(val\)。
#define lowbit(x) ((x)&(-x))
int c[N]; // 表示树状数组
int n; // 表示一共有多少个数
void add(int x, int val)
{
while (x <= n) {
c[x] += val;
x += lowbit(x);
}
}
5.2.2.2、查询前缀和
我们要查询 \(1 \sim x\) 这个区间的前缀和要怎么做呢?
根据我们之前对区间进行的划分,我们直接查询所有的区间就好了。
int query(int x)
{
int sum = 0;
while (x > 0) {
sum += c[x];
x -= lowbit(x);
}
return sum;
}
如果我们要查询单点的值怎么办呢?
直接用 query(x) - query(x-1) 就好了,当然如果 x==1 的话,就是求出来的答案。
如果是查询区间值的话,也是同样的道理。
至此,所有的 BIT 操作就讲完了,其他都是不同的应用,\(c\) 数组的含义不同。
所以,BIT 的本质其实就是,前缀和,但是我们可以在前缀和上进行修改,通过上面的推到,很容易算出, 单点加值,和查询前缀和 这两个查询的时间复杂度都是 \(log_n\) 的。
#include <bits/stdc++.h>
#define lowbit(x) ((x)&(-x)) // 一定要打括号!!!!
using namespace std;
typedef long long ll;
const int N = 1e6 + 10;
ll c[N]; // 树状数组
ll a[N]; // 原数组
int n, m; // n表示数的个数,m表示操作次数
void add(ll x, ll val)
{
while (x <= n) {
c[x] += val;
x += lowbit(x);
}
}
ll query(int x)
{
ll sum = 0;
while (x > 0) {
sum += c[x];
x -= lowbit(x);
}
return sum;
}
int main()
{
cin.tie(0)->sync_with_stdio(false);
cin >> n >> m;
for (int i = 1; i <= n; i++) { // 一般来说数据结构的题都从 1 开始存储
cin >> a[i];
add(i, a[i]); // 初始化
}
for (int i = 0; i < m; i++) {
int op, l, r;
cin >> op >> l >> r;
if (op == 1) {
add(l, r);
}
else {
cout << query(r) - query(l - 1) << endl;
}
}
return 0;
}
5.2.2.3、区间修改
区间加法的做法就是把 \(c\) 数组,定义为差分数组,我们在前面的单点修改中, \(c\) 数组中,直接存的就是原数组的前缀和,但是如果我们要支持区间修改的话,就需要把 \(c\) 数组定义为差分数组。add 和 query 函数都不用变换。
#include <bits/stdc++.h>
#define lowbit(x) ((x)&(-x)) // 一定要打括号!!!!
using namespace std;
typedef long long ll;
const int N = 1e6 + 10;
ll c[N]; // 树状数组
ll a[N]; // 原数组
int n, m; // n表示数的个数,m表示操作次数
void add(ll x, ll val)
{
while (x <= n) {
c[x] += val;
x += lowbit(x);
}
}
ll query(int x)
{
ll sum = 0;
while (x > 0) {
sum += c[x];
x -= lowbit(x);
}
return sum;
}
int main()
{
cin.tie(0)->sync_with_stdio(false);
cin >> n >> m;
for (int i = 1; i <= n; i++) { // 一般来说数据结构的题都从 1 开始存储
cin >> a[i];
}
for (int i = 0; i < m; i++) {
int op, l, r,val;
cin >> op >> l;
if (op == 1) {
cin >> r >> val;
add(l, val); // 差分操作
add(r + 1, val * (-1));
}
else {
cout << query(l) + a[l] << endl;
}
}
return 0;
}
可以看到这份代码和上面的代码,基本上没有什么改变,只有main里面的逻辑有一点点变化。
区间修改,区间查询,树状数组也是可以做到的,在逻辑上要稍微难一点,这里就不介绍了。
5.2.2.4、树状数组求逆序对
#include <bits/stdc++.h>
#define int long long
#define lowbit(x) ((x)&(-x));
using namespace std;
const int N = 5e5 + 10;
int b[N];
int n;
int sum[N];
void add(int x)
{
while (x <= n) { sum[x]++;x += lowbit(x); }
}
int query(int x)
{
int ans = 0;
while (x) {ans += sum[x]; x -= lowbit(x);}
return ans;
}
signed main()
{
cin.tie(0)->sync_with_stdio(false);
while (cin >> n && n ) {
vector<int> a;
memset(sum, 0x00, sizeof sum);
for (int i = 0; i < n; i++) {
int te; cin >> te; a.push_back(te);
b[i] = a[i];
}
// 离散化
sort(a.begin(), a.end());
a.erase(unique(a.begin(), a.end()), a.end());
for (int i = 0; i < n; i++) {
b[i] = (lower_bound(a.begin(), a.end(), b[i]) - a.begin()) + 1;
}
int ans = 0;
for (int i = 0; i < n; i++) {
// 当前放了i个数进去,我们求小于 b[i] 的数有多少个
// 那么 i - query(b[i]) 就代表的是大于 b[i]的有多少个数了
ans += i - query(b[i]);
add(b[i]);
}
cout << ans << endl;
}
return 0;
}
5.3、线段树(Segment Tree)
5.3.1____线段树概念
5.3.1.1____引入
有一类这样的问题 RMQ Range Minimum/Maximum Query问题,求区间最大值或最小值。设有长度为 \(n\) 的数列 {\(a_1,a_2,.. .,a_n\)} ,需要进行以下操作。
(1)求最值:给定 $ i,j \le n $ 求 {\(a_1,a_2,.. .,a_n\)} 中的最值。
(2)修改元素:给定 k 和 x 把,\(a_k\) 改为 x 。
5.3.1.2____什么是线段树
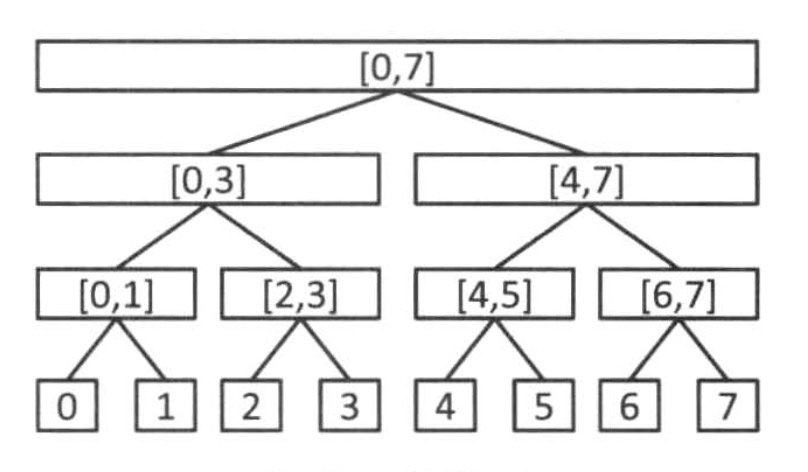
线段树是算法竞赛中常用的用来维护 区间信息 的数据结构,用完全二叉树来构造。
线段树可以在 \(\Theta (logN)\) 的时间复杂度内实现单点修改、单点查询、区间修改、区间查询(区间求和,求区间最大值,求区间最小值)等操作。
线段树的实现是基于分治思想的二叉树结构,用于在区间上进行信息通信。与按照二进制位(2的次幂)进行区间划分的树状数组相比,线段树是一种更加通用的数据结构:
- 线段树的每个结点都代表一个区间。
- 线段树具有唯一的根节点,代表的区间是整个统计范围,如 \([1,N]\)。
- 线段树的每个叶节点都代表一个长度为 \(1\) 的区间 \([x,x]\) ,表示一个数。
- 对于每个内部节点 \([l,r]\) ,他的左子节点(左儿子)是 \([l,mid]\) ,右子节点(右儿子)是 \([mid+1,r]\) ,其中 $mid = \left \lfloor (l+r)/2 \right \rfloor $ (向下取整)。
区间视角

二叉树视角
上图展示了一棵线段树。可以发现,除去最后一层,整棵线段树一定是一个完全二叉树,树的深度为 \(O(logN)\) 。因此,我们按照 父子2倍 节点编号:
- 根节点编号为 \(1\)。
- 编号为 \(x\) 的节点的左子节点编号为 \(x \cdot 2\) ,右子节点编号为 \(x \cdot 2 + 1\) 。
这样一来,我们就能简单的用一个 struct 数组来保存线段树。当然,树的最后一层节点在数组中保存的位置不是连续的,直接空出数组中多余的位置即可。
5.3.1.3____线段树的表示
线段树是建立在线段(或区间)基础上的树,树的每个结点代表一条线段 \([L,R]\)。
我们一般用struct来存储线段树的结点(也可以用多个数组来模拟,看个人喜好)
const int N = 1e5 + 5;
strcut Node
{
int l,r;
int sum;
}Tree[N<<2];
-
线段树的会提前把所有的会用到的结点的内存提前分配好,通过建树来初始化每一个结点使得区间和输入数组相对应。
-
$ l,r $ 表示此结点在在输入数组中所表示的区间,\(sum\) 看问题而定,可以是区间和,区间最值等等。
-
叶子结点的 \(l\) 值与 \(r\) 值相等,表示输入数组的下标(从1开始,为的是方便计算左右儿子)在 \(l\) (或 \(r\) )处的元素值。
-
每个非叶子结点都代表某些相邻叶子结点的合并。
-
由于线段树用完全二叉树构造,一个结点的左右儿子结点不用存储,直接通过公式计算。
假如我们的输入数组为 { 1 , 3 , 5 , 7 , 9 , 11 }
在数组中的结构:
Tree[] = {36, 9, 27, 4, 5, 16, 11, 1, 3, NULL, NULL, 7, 9, NULL, NULL}
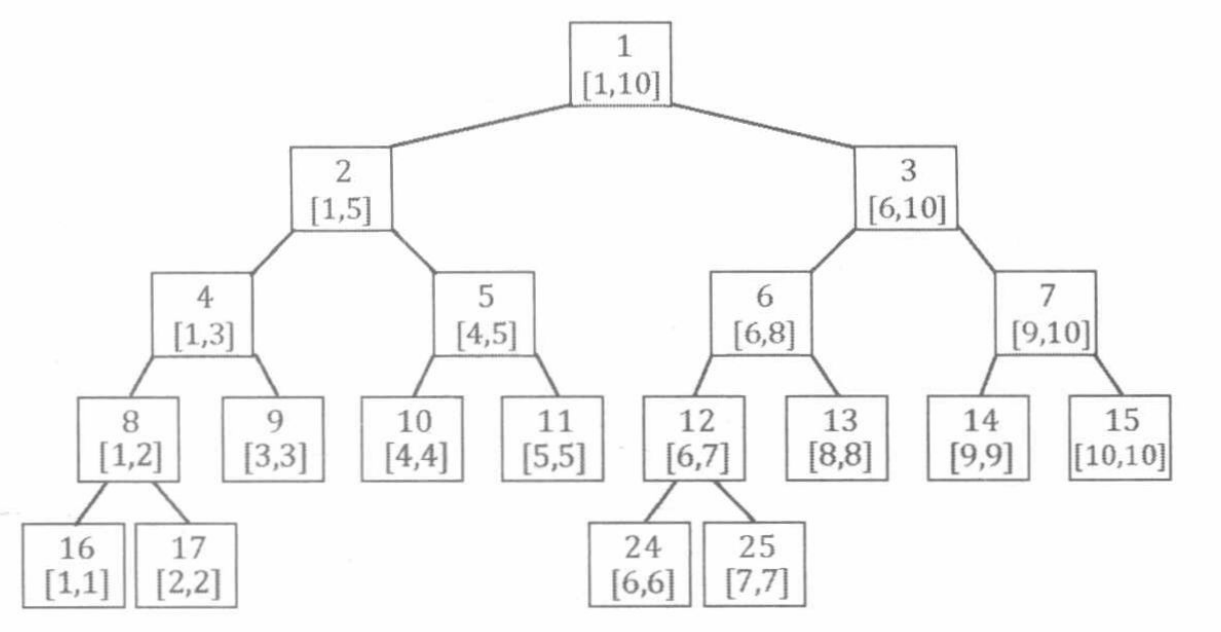
5.3.1.4____线段树的空间计算
如果 \(n\) 是2的幂次方,那么就不会出现有结点为NULL的情况,也就是说没有空间的浪费。在此情况下,线段树的结点个数为2n-1,有n个叶子结点,以及n-1个内部结点(非叶子结点)。
(可以数一下图中的内部结点和叶子结点的个数)
如果 \(n\) 不是2的幂次方,那么线段树的结点个数为 2x-1 (x为第一个比 \(n\) 大的 \(2\) 的幂次方数),但是在我们做题的时候通常直接多乘个 \(2\) 就好了( T[N*4] || T[N>>2] )
1.5____关于取左右儿子的问题
在之前的树形结构中,我们都是用指针来指向左右儿子。由于线段树基于完全二叉树实现,这一特性,我们可以直接算出每个结点对应的左右儿子结点的坐标。通过坐标的随意存取访问在效率上肯定是比指针更高的,但是别忘了完全二叉树存在空间的浪费,所以各有各的好,我们选择在比赛中对我们更好的解决办法。
-
左儿子:rt * 2rt << 1 -
右儿子:rt * 2 + 1rt << 1|1这里用位运算,可以提升运行效率,
5.3.2____单点修改,单点查询,区间查询
5.3.2.1____建树
建树我们是通过从 \([1,n]\) 开始,递归的把树建立起来(其过程类似DFS)
后面的代码都是以求区间和为例
void push_up(int rt)
{
Tree[rt].sum = Tree[rt << 1].sum + Tree[rt << 1|1].sum
}
void build(int rt,int l,int r)
{
Tree[rt].l = l , Tree[rt].r = r; // 结点 rt
if( l == r ){ /// 递归到了叶结点
Tree[rt].sum = A[r]; /// A为输入数组
return ;
}
int mid = l + r >> 1;
build( rt<<1 , l , mid );
build( rt<<1|1, mid + 1 , r );
push_up( rt );
}
5.3.2.2____单点修改
单点修改的过程和建树的过程类似,其过程相当于在树上二分。
在更新 \(a_i\) 的值时,需要对包含 \(i\) 所有区间对应结点的值重新进行计算。在更新时,可以从下面的结点开始向上不断更新,把每个结点的值更新为左右两个儿子的值的和就好。
一般这个过程我们用push_up函数来解决,在建树的时候我们也会执行这个操作。
void update(int rt,int pos,int val)
{
if( Tree[rt].l == Tree[rt].r ){ /// 如果到了pos这个位置就更新
A[pos] +=val;
Tree[rt].sum +=val;
return ; /// 一定要return
}
int mid = ( Tree[rt].l + Tree[rt].r ) >> 1;
if( pos <= mid ) update( rt << 1,pos,val ); /// 注意思考什么时候是if-else,什么时候是if-if
else update( rt << 1|1, pos, val );
push_up(rt); /// 更新父结点
}
5.3.2.3____单点查询
单点查询和单点更新基本相同
int update(int rt,int pos)
{
if( Tree[rt].l == Tree[rt].r ){ /// 如果到了pos这个位置就更新
return Tree[rt].sum; /// 一定要return
}
int mid = ( Tree[rt].l + Tree[rt].r ) >> 1;
int res = 0;
if( pos <= mid ) res = update( rt << 1,pos ); /// 注意思考什么时候是if-else,什么时候是if-if
else res = update( rt << 1|1, pos );
return res;
}
5.3.2.4____区间查询
区间查询和我们单点查询在思想上有点不同,还记得我前面代码中的注释吗?
区别if-else 以及if-if ,我们在单点修改的时候,我们的搜索树只会遍历到一个结点的左结点或右结点。但是在区间修改中,a我们可能把一个结点的左右儿子都遍历了,因为我们要求的区间在多数情况下是无法直接取得的(也就是说没有一个结点直接代表我们要求的整个区间)。
所有通常情况下,我们求解的区间是很多个区间的叠加,这也是线段树最难的地方,在后面因为区间取值的问题,我们会有很多复杂的操作(人话就是做好心理准备)。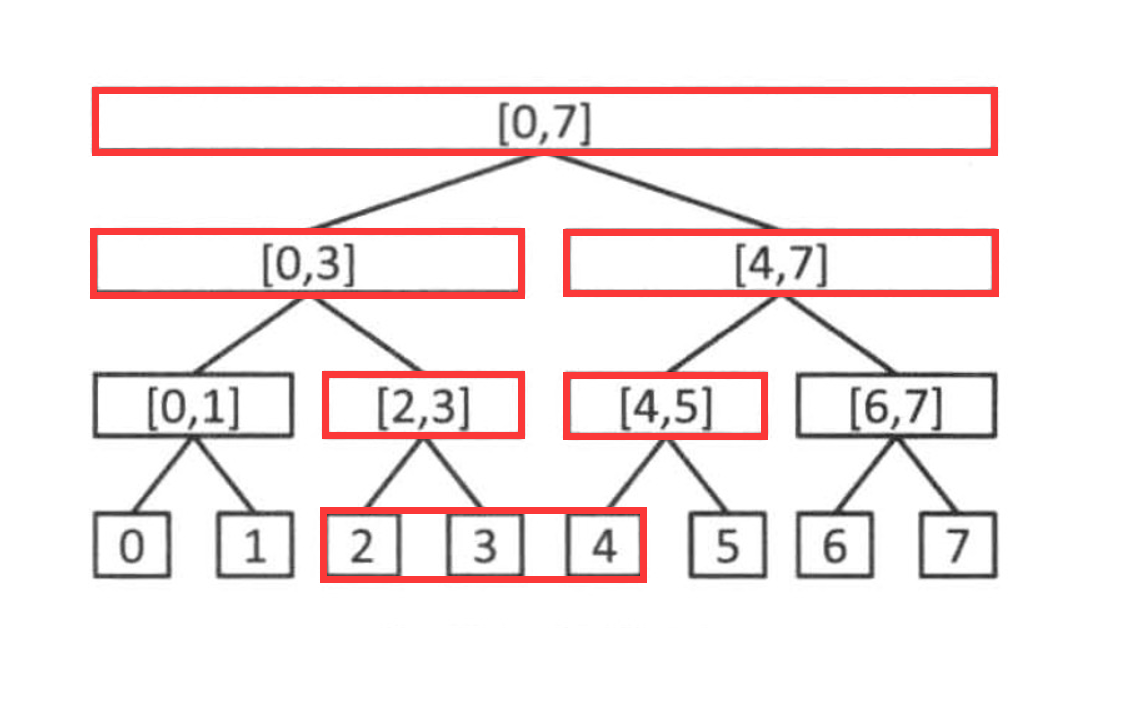
int update(int rt,int l,int r)
{
if( l <= Tree[rt].l && r >= Tree[rt].r ){ /// 如果到了pos这个位置就更新
return Tree[rt].sum; /// 一定要return
}
int mid = ( Tree[rt].l + Tree[rt].r ) >> 1;
int res = 0;
if( l <= mid ) res += update( rt << 1,l,r ); /// 注意思考什么时候是if-else,什么时候是if-if
if( r > mid ) res += update( rt << 1|1, l,r );
return res;
}
5.3.2.5____例题
例1
给定一个正整数数列 a1,a2,…,an,每一个数都在 0∼p−1 之间。
可以对这列数进行两种操作:
- 添加操作:向序列后添加一个数,序列长度变成 n+1;
- 询问操作:询问这个序列中最后 L 个数中最大的数是多少。
程序运行的最开始,整数序列为空。
一共要对整数序列进行 m 次操作。
写一个程序,读入操作的序列,并输出询问操作的答案。
输入格式
第一行有两个正整数 m,p,意义如题目描述;
接下来 m 行,每一行表示一个操作。
如果该行的内容是
Q L,则表示这个操作是询问序列中最后 L 个数的最大数是多少;如果是
A t,则表示向序列后面加一个数,加入的数是 (t+a) mod p。其中,t 是输入的参数,a 是在这个添加操作之前最后一个询问操作的答案(如果之前没有询问操作,则 a=0)。第一个操作一定是添加操作。对于询问操作,L>0 且不超过当前序列的长度。
输出格式
对于每一个询问操作,输出一行。该行只有一个数,即序列中最后 L 个数的最大数。
数据范围
\(1≤m≤2×10^5\)
\(1≤p≤2×10^9\)
0≤t<p输入样例:
10 100 A 97 Q 1 Q 1 A 17 Q 2 A 63 Q 1 Q 1 Q 3 A 99输出样例:
97 97 97 60 60 97样例解释
最后的序列是 97,14,60,96
#include <bits/stdc++.h>
using namespace std;
const int N = 2e5+10;
struct Node{
int l,r;
int sum;
}T[N<<2];
void push_up(int rt)
{
T[rt].sum = max(T[rt << 1].sum , T[rt << 1|1].sum);
}
void build(int rt,int l, int r)
{
T[rt] = {l,r,0};
if( T[rt].l == T[rt].r ){
return ;
}
int mid = (l + r) >> 1;
build(rt << 1,l,mid),build(rt <<1|1,mid+1,r);
push_up(rt);
}
void update(int rt,int pos,int val)
{
if( T[rt].l == T[rt].r && T[rt].r == pos ){
T[rt].sum = val;
return ;
}
int mid = ( T[rt].l + T[rt].r ) >>1;
if( pos <= mid ) update(rt <<1,pos,val);
else update(rt <<1|1,pos,val);
push_up(rt);
}
int query(int rt,int l,int r)
{
if( l <= T[rt].l && r >= T[rt].r ){
return T[rt].sum;
}
int mid = (T[rt].l + T[rt].r) >> 1;
int l_son = 0,r_son = 0;
if( l <= mid ) l_son = query(rt <<1,l,r);
if( r > mid ) r_son += query(rt <<1|1,l,r);
return max(l_son,r_son);
}
int main()
{
ios::sync_with_stdio(false);
cin.tie(nullptr);
cout.tie(nullptr);
int n,p,res = 0 ,cnt = 1;
cin >> n >> p;
build(1,1,n);
for(int i = 0; i < n ; i++){
char c;
int x;
cin>> c>>x;
if( c == 'A' ){
update(1,cnt++, (x+res)%p );
}else{
res = query( 1,cnt - x,cnt-1 );
cout <<res << "\n";
}
}
return 0;
}
5.3.3____区间修改,Lazy标记
首先我们来思考一下,之前我们在线段树上做的修改操作,是单点修改,如果我们现在想要对一个区间都进行同一个操作(区间加,区间减等)呢?
我们一次单点修改的时间复杂度是 \(O(log_n)\) ,那么如果要修改的区间长度为 \(m\) 那么用单点修改的方式就会变成 \(O(mlog_n)\) ,显然这个结果是很低效的,所以我们才有了 \(Lazy\) 标记。
试想一下,如果我们在一次修改指令中发现节点 \(p\) 代表的区间 \([p_l,p_r]\) 被修改区间 \([l,r]\) 完全覆盖(例如下图我们要查找的区间是 [2,4],代表 [2,3]的节点就被完全覆盖),并且逐一更新了子树 \(p\) 中的所有节点,但是在之后的查询指令中却根本没有用到 \([l,r]\) 的子区间作为候选答案,那么更新 \(p\) 的整个子树做的都是无用功。

换言之,我们在执行修改指令时,同样可以在 \(l \le p_l \le p_r \le r\) 的情况下就立即返回 ,只不过在回溯之前向节点 \(p\) 增加一个标记,表示 这个节点曾经被修改,但其子节点还未被更新。
如果在后续的治疗中,需要从节点 \(p\) 向下递归,我们再检查 \(p\) 是否具有标记。若有标记,就根据标记信息更新 \(p\) 的两个子节点,同时为 \(p\) 的;两个子节点增加标记,然后清楚 \(p\) 节点的标记。
也就是说,除了在修改指令中直接划分的 \(O(log_N)\) 个结点之外,对任意结点的修改都延迟到 后续操作中递归进入他的父节点时再来执行。这样一来,每条查询或修改指令的时间复杂度都降低到了 \(O(log_N)\) 。
这就是 Lazy 标记 ,提供了线段树中,从上往下传递信息的方式。
5.3.3.2____push_down lazy 标记下传
void push_down(int rt)
{
/// 如果lazy标记非空,我们就把标记下传
if( Tree[rt].lazy != 0 ){
int mid = (Tree[rt].l + Tree[rt].r) >> 1;
/// 更新子节点
Tree[rt << 1].sum += Tree[rt].lazy * ( mid - Tree[rt].l + 1); /// 注意这后面的值
Tree[rt << 1 | 1].sum += Tree[rt].lazy * ( Tree[rt].r - mid) ; /// 注意这后面的值
/// 继续把标记下传
Tree[rt << 1].lazy += Tree[rt].lazy;
Tree[rt << 1|1].lazy += Treert].lazy;
/// 清空当前节点的lazy标记
Tree[rt].lazy = 0;
}
}
5.3.3.3____带lazy标记的,区间修改
void rangeUpdate(int rt, int l,int r,int val)
{
if( l <= Tree[rt].l && r >= Tree[rt].r ){
Tree[rt].sum += val * (Tree[rt].r - Tree[rt].l + 1); /// 把所有的区间中的值都先修改
Tree[rt].lazy += val;
return ;
}
int mid = ( Tree[rt].l + Tree[rt].r ) >> 1;
push_down(rt); /// 标记下传
if( l <= mid ) rangeUpdate( rt << 1,l,r,val );
if( r > mid ) rangeUpdate( rt << 1|1,l,r,val );
push_up(rt); /// 区间值上传
}
5.3.3.4____带标记下传的区间查询
ll rangeQuery(int rt,int l ,int r)
{
if( l <= Tree[rt].l && r >= Tree[rt].r ){
return Tree[rt].sum;
}
ll mid = ( Tree[rt].l + Tree[rt].r ) >> 1;
push_down(rt); /// 标记下传
ll son = 0;
if( l <= mid ) son += rangeQuery(rt << 1,l,r); /// 查询左儿子
if( r > mid ) son += rangeQuery(rt << 1|1,l,r); /// 查询右儿子
push_up(rt);
return son;
}
5.3.3.5____例题
A Simple Problem with Integers - POJ 3468
You have N integers, \(A_1, A_2, ... , A_N\). You need to deal with two kinds of operations. One type of operation is to add some given number to each number in a given interval. The other is to ask for the sum of numbers in a given interval.
Input
The first line contains two numbers N and Q. 1 ≤ N,Q ≤ 100000.
The second line contains N numbers, the initial values of A1, A2, ... , AN. -1000000000 ≤ Ai ≤ 1000000000.
Each of the next Q lines represents an operation.
"C a b c" means adding c to each of Aa, Aa+1, ... , Ab. -10000 ≤ c ≤ 10000.
"Q a b" means querying the sum of Aa, Aa+1, ... , Ab.Output
You need to answer all Q commands in order. One answer in a line.
Sample Input
10 5 1 2 3 4 5 6 7 8 9 10 Q 4 4 Q 1 10 Q 2 4 C 3 6 3 Q 2 4Sample Output
4 55 9 15
#include <iostream>
#include <algorithm>
using namespace std;
const int N = 1e5 + 10;
typedef long long ll;
ll a[N];
struct Node
{
ll l ,r;
ll sum;
ll lazy;
}T[N<<2];
void push_up(int rt)
{
T[rt].sum = T[rt << 1].sum + T[rt << 1|1].sum;
}
void push_down(int rt)
{
if( T[rt].lazy != 0 ){
int mid = (T[rt].l + T[rt].r) >> 1;
T[rt << 1].sum += T[rt].lazy * ( mid - T[rt].l + 1);
T[rt << 1 | 1].sum += T[rt].lazy * ( T[rt].r - mid) ;
T[rt << 1].lazy += T[rt].lazy;
T[rt << 1|1].lazy += T[rt].lazy;
T[rt].lazy = 0;
}
}
void build(int rt,int l,int r)
{
T[rt] = {l,r,0,0};
if( l == r ){
T[rt].sum = a[l];
return ;
}
int mid = (l + r) >> 1;
build(rt<<1,l,mid),build(rt <<1|1,mid+1,r);
push_up(rt);
}
void rangeUpdate(int rt, int l,int r,int val)
{
if( l <= T[rt].l && r >= T[rt].r ){
T[rt].sum += val * (T[rt].r - T[rt].l + 1);
T[rt].lazy += val;
return ;
}
int mid = ( T[rt].l + T[rt].r ) >> 1;
push_down(rt);
if( l <= mid ) rangeUpdate( rt << 1,l,r,val );
if( r > mid ) rangeUpdate( rt << 1|1,l,r,val );
push_up(rt);
}
ll rangeQuery(int rt,int l ,int r)
{
if( l <= T[rt].l && r >= T[rt].r ){
return T[rt].sum;
}
ll mid = ( T[rt].l + T[rt].r ) >> 1;
push_down(rt);
ll son = 0;
if( l <= mid ) son += rangeQuery(rt << 1,l,r);
if( r > mid ) son += rangeQuery(rt << 1|1,l,r);
push_up(rt);
return son;
}
int main()
{
ios::sync_with_stdio(false);
cin.tie(0);
cout.tie(0);
int n,m;
cin >> n >> m;
for(int i = 1 ; i <= n ; i ++ ) cin >> a[i];
build(1,1,n);
for(int i = 0 ; i < m ; i++ ){
char op ;
ll x,y,z;
cin >> op;
if( op == 'C' ){
cin >> x >> y >> z;
rangeUpdate(1,x,y,z);
}else{
cin >> x >> y;
cout << rangeQuery(1,x,y) << "\n";
}
}
return 0;
}
5.3.4、最大子段和问题
5.3.5、势能线段树
5.3.6、动态开点线段树
5.3.7、线段树合并
[P2824 HEOI2016/TJOI2016]排序 - 洛谷 | 计算机科学教育新生态 (luogu.com.cn)
5.3.x____习题
Mayor's posters
AB市,字节城的市民无法忍受在市长竞选活动中,候选人随心所欲的在各处张贴选举海报。所以字节城的市民最终决定建立一个选民墙来介绍这些信息,规则如下:
每个候选人都可以在墙上贴一张海报。
每张海报高度和这个选民墙的高度一致;宽度可以是任意的整数字节(字节是整个城市的长度单位)。
这个信息墙被分成几段,每段的宽度是一个字节。
每张海报必须完全覆盖连续的墙段。
字节城的市民建立了一个长度为 $ 1e7$ 的选民墙(如此就有足够的空间给候选人来张贴自己的海报)。当竞选活动重新开始时,候选人在墙上张贴自己的海报,海报与海报之间的宽度相差很大。此外,候选人开始把他们的海报张贴在已经被其他海报占据的墙上。字节城的每个人都很好奇,在选举的最后一天,谁的海报会被看到(全部或部分)。
你的任务是计数到最后有多少张海报可以被看到。
#include <set>
#include <algorithm>
#include <iostream>
#include <vector>
#define ls rt << 1
#define rs rt << 1|1
using namespace std;
const int N = 1e5 + 10;
const int INF = 0x3f3f3f3f;
struct Node
{
int l,r;
int tp;
int lazy;
}T[N << 2];
inline void push_down(int rt)
{
if( T[rt].lazy != 0 ){
T[ls].tp = T[rt].lazy;
T[ls].lazy = T[rt].lazy;
T[rs].tp = T[rt].lazy;
T[rs].lazy = T[rt].lazy;
T[rt].lazy = 0;
}
}
inline void push_up(int rt)
{
if( T[ls].tp != T[rs].tp ) T[rt].tp = INF;
else T[rt].tp = T[ls].tp;
}
void build(int rt,int l,int r)
{
T[rt] = {l,r,0,0};
if( l == r ){
return;
}
int mid = (l + r) >> 1;
build(ls,l,mid),build(rs,mid+1,r);
}
inline void rangeUpdate(int rt,int l,int r,int val)
{
if( l <= T[rt].l && r >= T[rt].r ){
T[rt].tp = val;
T[rt].lazy = val;
return ;
}
int mid = (T[rt].l + T[rt].r) >>1;
push_down(rt);
if( l <= mid ) rangeUpdate( ls,l,r,val );
if( r > mid ) rangeUpdate( rs,l,r,val );
push_up(rt);
}
inline int getTpye(int rt,int pos)
{
if( T[rt].l == T[rt].r && T[rt].l == pos ){
return T[rt].tp;
}
int mid = ( T[rt].l + T[rt].r ) >>1;
int son = 0;
push_down(rt);
if(pos <= mid) son = getTpye( ls,pos );
else son = getTpye(rs,pos);
return son;
}
int main()
{
ios::sync_with_stdio(false);
cin.tie(0);
cout.tie(0);
int k;
cin >> k;
while(k--){
int n;
cin >> n;
///离散化
vector<pair<int,int> > a(n);
vector<int> ans;
for(int i = 0; i < n ; i ++){
cin >> a[i].first >> a[i].second;
ans.push_back(a[i].first);
ans.push_back(a[i].second);
}
sort(ans.begin(),ans.end());
ans.erase( unique(ans.begin(),ans.end()),ans.end() );
int len = ans.size();
for(int i = 1 ; i < len; i ++){
if( ans[i] - ans[i-1] > 1 ){
ans.push_back( ans[i-1] + 1 );
}
}
sort(ans.begin(),ans.end());
// for(int i = 0 ; i < ans.size() ; i++ ){
// cout << ans[i] << " \n"[i == ans.size()];
// }
build(1,1,ans.size());
/// 贴海报
len = a.size();
for(int i =0 ; i < len ; i++){
int x = lower_bound(ans.begin(), ans.end() , a[i].first) - ans.begin() + 1;
int y = lower_bound(ans.begin(), ans.end() , a[i].second) - ans.begin() + 1;
rangeUpdate( 1,x,y,i+1 );
}
//cout <<endl;
len = ans.size();
set<int> se;
for(int i = 1 ; i <= len ; i++ ){
int te = getTpye(1,i);
se.insert( te );
}
se.erase(0);
cout <<se.size() <<endl;
}
return 0;
}
Balanced Lineup
在日常的挤奶任务中,John的 N 头牛总是排成一条线,并且顺序不会改变。一天,John决定和一些奶牛组织一场极限飞盘游戏。为了方便,他会选择在牛群中连续的一群牛来玩这个游戏。然而为了让所有的牛都能愉快的玩耍,所选的牛之间的升高差距不能太大。
他需要你的帮助来确定这群牛中最矮和最高的牛之间的身高差异。
维护区间最大值,最小值
#include <iostream>
#include <algorithm>
#include <cmath>
using namespace std;
typedef pair<int,int> pir;
const int N = 5e4+10;
int a[N];
struct Node
{
int l,r;
int ma;
int mi;
}T[N<<2];
void push_up(int rt)
{
T[rt].ma = max( T[rt<<1].ma,T[rt<<1|1].ma );
T[rt].mi = min( T[rt<<1].mi,T[rt<<1|1].mi );
}
void build(int rt,int l,int r)
{
T[rt] = {l,r,0,0};
if( l == r ){
T[rt].ma = T[rt].mi = a[l];
return ;
}
int mid = ( l + r ) >> 1;
build(rt <<1,l,mid),build(rt<<1|1,mid+1,r);
push_up(rt);
}
pir rangeQuery(int rt ,int l ,int r)
{
if( l <= T[rt].l && r >= T[rt].r ){
return {T[rt].ma,T[rt].mi};
}
int mid = (T[rt].l + T[rt].r) >>1;
pir l_son,r_son;
l_son = r_son = { 0,2000000 };
if( l <= mid ) l_son = rangeQuery(rt<<1,l,r);
if( r > mid ) r_son = rangeQuery(rt<<1|1,l,r);
return { max(l_son.first,r_son.first) , min( l_son.second,r_son.second ) };
}
int main()
{
ios::sync_with_stdio(false);
cin.tie(0);
cout.tie(0);
int n,m;
cin >> n >>m;
for(int i = 1; i <= n ; i ++) cin >> a[i];
build(1,1,n);
//
// for(int i = 1; i < 15 ; i++){
// cout << T[i].ma << endl;
// }
for(int i = 0 ; i < m ; i++){
int x,y;
cin >>x >>y;
pir ans = rangeQuery(1,x,y);
cout << ans.first-ans.second << endl;
}
return 0;
}
Can you answer these queries?
如果是0就把区间开根,1就查询区间
#include <bits/stdc++.h>
using namespace std;
typedef long long ll;
const int N = 1e5+5;
ll A[N];
struct Node
{
ll l,r;
ll sum;
}tree[N*4];
inline void push_up( ll rt)
{
tree[rt].sum = tree[rt<< 1].sum + tree[rt << 1|1].sum;
}
inline void build( ll rt, ll l, ll r)
{
tree[rt].l = l ,tree[rt].r = r;
if(l == r)
tree[rt].sum = A[r];
else
{
ll mid = (l + r) >> 1;
build(rt << 1,l ,mid);
build(rt << 1|1,mid +1 ,r);
push_up(rt);
}
}
inline void Update(int rt,int l,int r)
{
if( tree[rt].l == tree[rt].r)
{
tree[rt].sum = (ll)sqrt( (double)tree[rt].sum );
return ;
}
if( l <= tree[rt].l && r >= tree[rt].r && tree[rt].sum == tree[rt].r - tree[rt].l + 1 ) return ;
ll res = 0;
ll mid = ( tree[rt].l + tree[rt].r ) >> 1;
if( l <= mid ) Update(rt << 1,l ,r);
if( r > mid ) Update( rt << 1|1,l,r );
push_up(rt);
}
inline ll Query(int rt,int l,int r)
{
if( l <= tree[rt].l && r >= tree[rt].r ) return tree[rt].sum;
int mid = (tree[rt].l + tree[rt].r) >> 1;
ll res = 0;
if( l <= mid ) res += Query(rt << 1,l , r);
if( r > mid ) res += Query(rt << 1|1,l ,r);
return res ;
}
int main()
{
ios::sync_with_stdio(false);
cin.tie(0);
int n,m;
int cnt = 1;
while(cin >> n)
{
cout << "Case #" << cnt++ <<':' <<endl;
for(int i = 1; i <= n ; i++) cin >> A[i];
build(1,1,n);
cin >> m;
for(int i = 0 ; i < n ; i++)
{
int cmd,x,y;
cin >> cmd >>x >>y;
if( x > y) swap(x,y);
if( cmd == 1)
{
cout << Query(1 ,x,y) <<endl;
}
else
{
Update(1,x,y);
}
}
cout << endl;
}
return 0;
}
I Hate It
#include <bits/stdc++.h>
using namespace std;
const int N = 200005;
int A[N],tree[N*4];
void push_up(int rt)
{
tree[rt] = max(tree[rt << 1] , tree[rt<<1|1]) ;
}
void build(int rt,int l ,int r)
{
if( l == r)
{
tree[rt] = A[r];
}
else
{
int mid = (l + r) >>1;
build(rt << 1, l ,mid);
build(rt << 1|1 , mid +1 , r);
push_up(rt);
}
}
void Update(int rt,int l,int r ,int pos,int val)
{
if( r == l )
{
tree[rt] = val;
A[pos] = val;
return ;
}
else
{
int mid = (l + r) >> 1;
if( pos <= mid ) Update( rt << 1,l ,mid,pos,val );
else Update( rt<<1|1 ,mid +1, r,pos,val );
push_up(rt);
}
}
int Query(int rt,int l, int r ,int start,int ed)
{
if( l > ed || r < start ) return 0;
if( start <= l && ed >= r ) return tree[rt];
else
{
int mid = (l + r) >> 1;
int l_son = Query(rt << 1,l,mid,start,ed);
int r_son = Query(rt << 1|1,mid+1,r,start,ed);
return max(l_son , r_son);
}
}
int main()
{
ios::sync_with_stdio(false);
cin.tie(0);
int n ,m;
while(cin >> n>> m)
{
for(int i = 1; i <= n ; i++) cin >> A[i];
build( 1,1,n );
for(int i = 1; i <= m ; i++)
{
char cmd;
int x,y;
cin >> cmd >>x >> y;
if( cmd == 'Q' ){
cout << Query(1,1,n,x,y) << endl;
}
else{
Update(1,1,n,x,y);
}
}
}
return 0;
}
5.4、单调栈
单调栈,顾名思义就是在一个栈中的元素都是单调递增的。其可维护一个数的, 左/右边,第一个 大/小于 这个数的数。
左边一个比他小的数
int n; cin >> n;
for (int i = 0; i < n; i++)cin >> a[i];
for (int i = 0; i < n; i++) {
// 如果破坏了单调性,就去除
while (tot && sta[tot] >= a[i]) tot--;
if (!tot) ans[i] = -1;
else ans[i] = sta[tot]; // sta[] 为数组模拟的栈,tot为栈顶指针
sta[++tot] = a[i];
}
for (int i = 0; i < n; i++) cout << ans[i] << ' ';cout << endl;
- 左边第一个比他大的数
int n; cin >> n;
for (int i = 0; i < n; i++)cin >> a[i];
for (int i = 0; i < n; i++) {
while (tot && a[i] >= sta[tot]) tot--;
if (!tot) ans[i] = -1;
else ans[i] = sta[tot];
sta[++tot] = a[i];
}
for (int i = 0; i < n; i++)cout << ans[i] << ' ';cout << endl;
- 右边第一个比他小的数
在求右边的时候我们都需要倒过来入栈,把需要更新答案的位置入栈,碰到右边满足调整的,再出栈,并记录结构
for (int i = 0; i < n; i++)cin >> a[i];
memset(ans, -1, sizeof ans);
for (int i = 0; i < n; i++) {
while (tot && a[i] < a[sta[tot]]) {
ans[sta[tot]] = a[i]; tot--;
}
sta[++tot] = i;
}
for (int i = 0; i < n; i++)cout << ans[i] << ' '; cout << endl;
- 右边第一个比他大的数
// 不是上题的标准代码,但是改改就可以了
for (int i = 0; i < n; i++)cin >> a[i];
memset(ans, -1, sizeof ans);
for (int i = 0; i < n; i++) {
//if (!tot) { sta[++tot] = i; continue; }
while (tot && a[i] > a[sta[tot]] ) {
ans[sta[tot]] = a[i]; tot--;
}
sta[++tot] = i;
}
for (int i = 0; i < n; i++)cout << ans[i] << ' '; cout << endl;
单调栈算法的时间复杂度为 O(n)。借助单调性处理问题的思想在于及时排除不可能的选项,保持策略集合的高度有效性和秩序性。
5.5、单调队列
- 用队列维护集合的最值
- 删除没有用的元素
- 队列就有单调性
O(1)取队头,找最值
int n,m; cin >> n >> m;
for (int i = 1; i <= n; i++) {
cin >> sum[i]; sum[i] += sum[i - 1];
}
int ma = -0x3f3f3f3f; /// 模拟队列,hh为队头,tt为队尾
for (int i = 1; i <= n; i++) {
if (q[hh] < i - m) hh++;
while (tt >= hh && sum[q[tt]] >= sum[i]) tt--;
ma = max(ma, sum[i] - sum[q[hh]]);
q[++tt] = i;
}
cout << ma << endl;
6、动态规划
6.1、线性DP
6.1.1、最长上升子序列 (Longest increasing subsequence)
| LIS | n^2 版本 |
|---|---|
| 状态表示 | dp[i] 表示以 a[i] 结尾的 最长上升子序列长度 |
| 区间划分 |
const int N = 1e3 + 10;
int a[N]; /// 原数组
int dp[N]; /// dp[i] 表示以 a[i] 结尾的 最长上升子序列长度
int main()
{
cin.tie(0)->sync_with_stdio(false);
int n; cin >> n;
for (int i = 1; i <= n; i++)cin >> a[i], dp[i] = 1;
int ma = 0;
for (int i = 1; i <= n; i++) {
for (int j = 1; j < i; j++) {
if (a[i] > a[j]) dp[i] = max(dp[i], dp[j] + 1);
}
ma = max(ma, dp[i]);
}
cout << ma << endl;
return 0;
}
| LIS | nlogn 版本 |
|---|---|
| 状态表示 | dp[i] 表示长度为 i 的最长上升子序列,最小的结尾是哪个 |
| 区间划分 |
const int N = 1e5 + 10;
int a[N];
int dp[N]; //dp[i] 表示长度为 i 的最长上升子序列,最小的结尾是哪个
int main()
{
cin.tie(0)->sync_with_stdio(false);
int n; cin >> n;
for (int i = 1; i <= n; i++)cin >> a[i];
int cnt = 1; dp[1] = a[1];
for (int i = 2; i <= n; i++) {
if (a[i] > dp[cnt]) dp[++cnt] = a[i];
else {
int loc = lower_bound(dp + 1, dp + cnt + 1, a[i]) - dp;
dp[loc] = a[i];
}
}
cout << cnt << endl;
return 0;
}
6.1.2、最长公共子序列问题(Longest common subsequence)
const int N = 1e3 + 10;
char a[N],b[N];
int dp[N][N];
int main()
{
cin.tie(0)->sync_with_stdio(false);
int n, m; cin >> n >> m;
for (int i = 1; i <= n; i++)cin >> a[i];
for (int i = 1; i <= m; i++)cin >> b[i];
for (int i = 1; i <= n; i++) {
for (int j = 1; j <= m; j++) {
if (a[i] != b[j]) dp[i][j] = max(dp[i][j - 1], dp[i - 1][j]);
else dp[i][j] = dp[i - 1][j - 1] + 1;
}
}
cout << dp[n][m] << endl;
return 0;
}
6.1.3、最长公共上升子序列 (Longest common increasing subsequence)
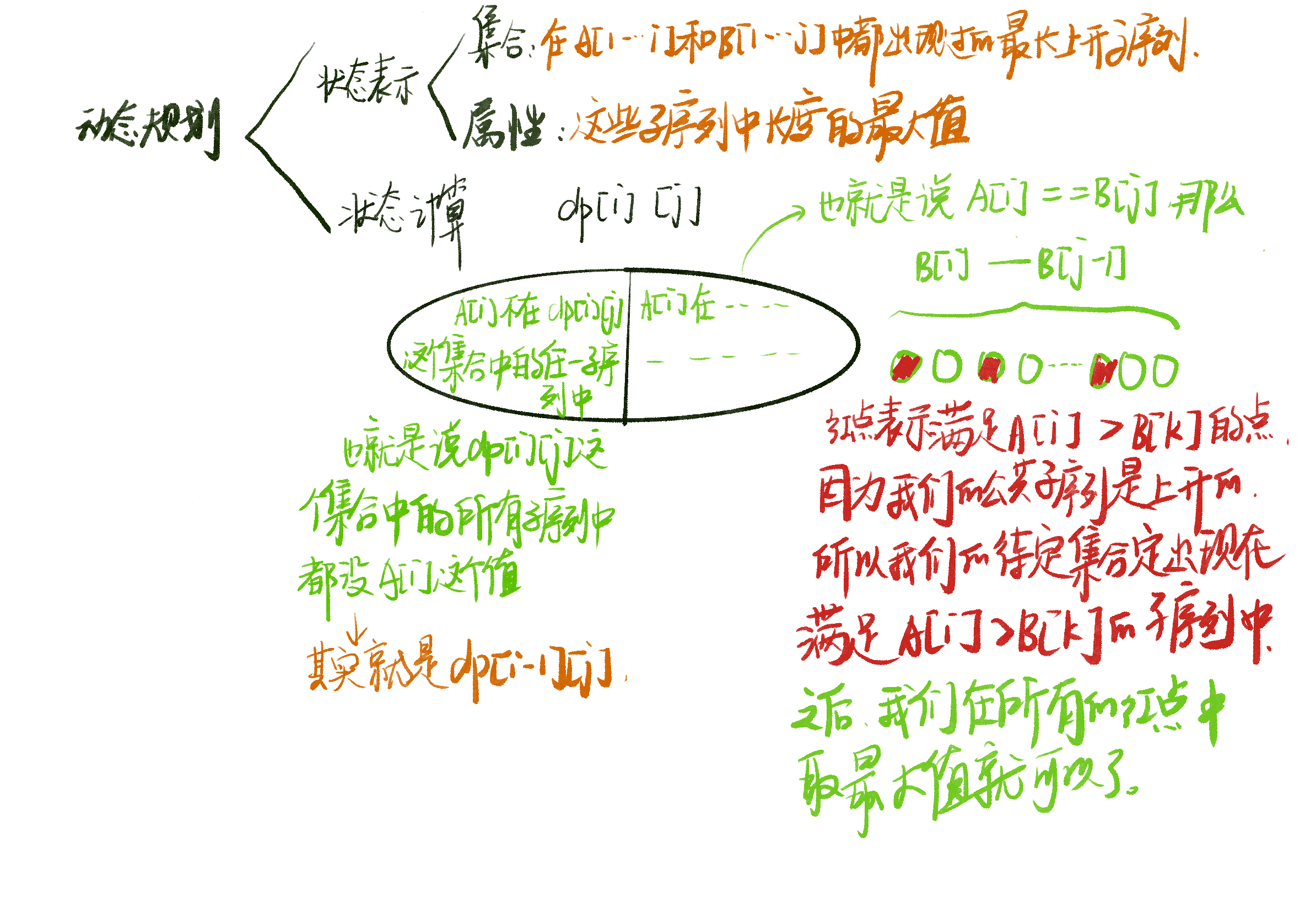
我们先按照思路写出 \(O(n^3)\) 的算法
#include <bits/stdc++.h>
using namespace std;
const int N = 3e3 + 10;
int dp[N][N];
int a[N], b[N];
int main()
{
cin.tie(0)->sync_with_stdio(false);
int n; cin >> n;
for (int i = 1; i <= n; i++)cin >> a[i];
for (int i = 1; i <= n; i++)cin >> b[i];
for (int i = 1; i <= n; i++) {
for (int j = 1; j <= n; j++) {
dp[i][j] = dp[i - 1][j];
if (a[i] == b[j]) {
for (int k = 1; k < j; k++) {
if (a[i] > b[k])dp[i][j] = max({ dp[i][j], dp[i][k] + 1 });
}
/// j = 1的情况,不会进入循环
dp[i][j] = max(1, dp[i][j]);
}
}
}
int res = 0;
for (int i = 1; i <= n; i++)res = max(res, dp[n][i]);
cout << res << endl;
return 0;
}
在 \(n= 3000\) 的时间复杂的下,显然时间复杂度太高了,所以我们要采取一定的优化。我们观察第三层循环:

这样我们就可以用一个值来不断更新最大值就好了。
#include <bits/stdc++.h>
using namespace std;
const int N = 3e3 + 10;
int dp[N][N];
int a[N], b[N];
int main()
{
cin.tie(0)->sync_with_stdio(false);
int n; cin >> n;
for (int i = 1; i <= n; i++)cin >> a[i];
for (int i = 1; i <= n; i++)cin >> b[i];
for (int i = 1; i <= n; i++) {
int maxv = 0;
for (int j = 1; j <= n; j++) {
dp[i][j] = dp[i - 1][j];
if (a[i] == b[j]) dp[i][j] = max(dp[i][j], maxv+1);
if (a[i] > b[j])maxv = max(maxv, dp[i - 1][j]);
}
}
int res = 0;
for (int i = 1; i <= n; i++)res = max(res, dp[n][i]);
cout << res << endl;
return 0;
}
6.1.4、分级
给定长度为 N 的序列 A,构造一个长度为 N 的序列 B,满足:
- BB 非严格单调,即 B1≤B2≤…≤BN 或 B1≥B2≥…≥BN。
- 最小化 \(S=\sum^{N}_{i=1}|A_i - B_i|\)。
只需要求出这个最小值 S。

#include <bits/stdc++.h>
using namespace std;
const int N = 2e3 + 10,inf = 0x3f3f3f3f;
int dp[N][N];
int a[N], b[N];
int n;
int work()
{
for (int i = 1; i <= n; i++)b[i] = a[i];
sort(b + 1, b + 1 + n);
for (int i = 1; i <= n; i++) {
int minv = inf;
for (int j = 1; j <= n; j++) {
minv = min(minv, dp[i-1][j]);
dp[i][j] = minv + abs(a[i] - b[j]);
}
}
int res = inf;
for (int i = 1; i <= n; i++)res = min(res, dp[n][i]);
return res;
}
int main()
{
cin.tie(0)->sync_with_stdio(false);
cin >> n;
for (int i = 1; i <= n; i++)cin >> a[i];
int res = work();
reverse(a + 1, a + 1 + n);
res = min(res, work());
cout << res << endl;
return 0;
}
6.1.5、移动服务
一个公司有三个移动服务员,最初分别在位置 1,2,3 处。
如果某个位置(用一个整数表示)有一个请求,那么公司必须指派某名员工赶到那个地方去。
某一时刻只有一个员工能移动,且不允许在同样的位置出现两个员工。
从 p 到 q 移动一个员工,需要花费 c(p,q)。
这个函数不一定对称,但保证 c(p,p)=0。
给出 N 个请求,请求发生的位置分别为 p1∼pN。
公司必须按顺序依次满足所有请求,且过程中不能去其他额外的位置,目标是最小化公司花费,请你帮忙计算这个最小花费。
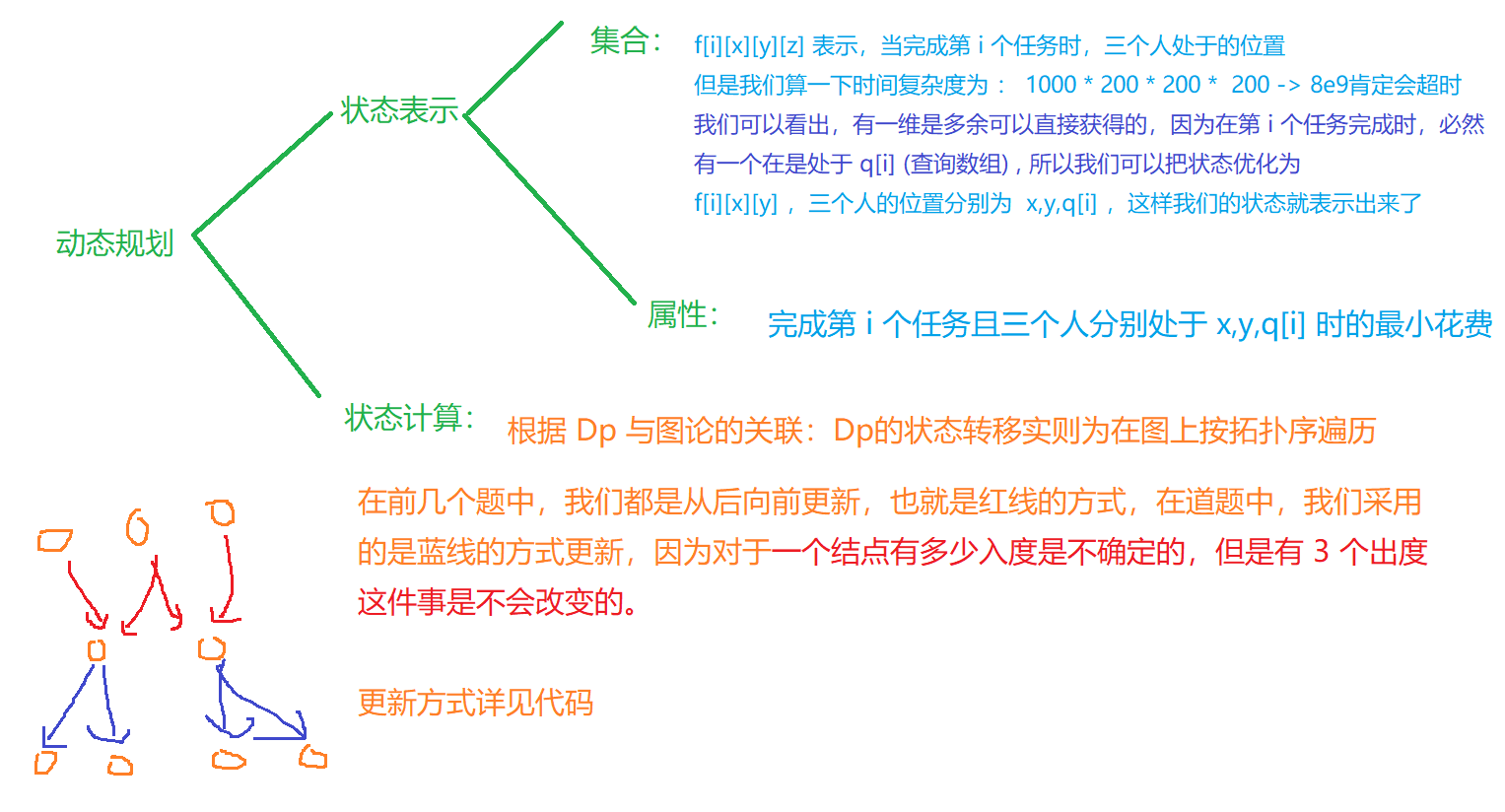
#include <bits/stdc++.h>
using namespace std;
const int N = 210, L = 1010;
int dp[L][N][N];
int w[N][N];
int q[L];
int main()
{
cin.tie(0)->sync_with_stdio(false);
int n, l; cin >> l >> n;
for (int i = 1; i <= l; i++)for (int j = 1; j <= l; j++)cin >> w[i][j];
for (int i = 1; i <= n; i++)cin >> q[i];
memset(dp, 0x3f, sizeof dp);
q[0] = 3;
dp[0][1][2] = 0;
for(int i = 0; i <= n ; i++)
for (int j = 1; j <= l; j++) {
for (int k = 1; k <= l; k++) {
int no = q[i],ne = q[i+1] ,val = dp[i][j][k];
if (j == k || j == no || k == no) continue; // 任意两人不能在同一点
// j 第一个人 ,k 第二个人, no 第三个人
// 派 j 去 ne
dp[i + 1][k][no] = min(dp[i + 1][k][no], val + w[j][ne]);
// 派 k 去 ne
dp[i + 1][j][no] = min(dp[i + 1][j][no], val + w[k][ne]);
// 派 no 去 ne
dp[i + 1][j][k] = min(dp[i + 1][j][k], val + w[no][ne]);
}
}
int res = 0x3f3f3f3f;
for (int i = 1; i <= l; i++)for (int j = 1; j <= l; j++) {
int no = q[n];
if (i == j || i == no || j == no) continue; // 任意两人不能在同一点
res = min(res, dp[n][i][j]);
}
cout << res << endl;
return 0;
}
6.1.6、饼干
圣诞老人共有 M 个饼干,准备全部分给 N 个孩子。
每个孩子有一个贪婪度,第 ii 个孩子的贪婪度为 g[i]。
如果有 a[i] 个孩子拿到的饼干数比第 i 个孩子多,那么第 i 个孩子会产生 g[i]×a[i]的怨气。
给定 N、M和序列 g,圣诞老人请你帮他安排一种分配方式,使得每个孩子至少分到一块饼干,并且所有孩子的怨气总和最小。
首先由贪心中的 排序不等式 我们可以知道 g[i] 越大的孩子,应该得到更多的饼干,如果对 g[i] 从大到小排序,那么这个序列从左到右获得的饼干数量也应该是单独递减的(非严格)。
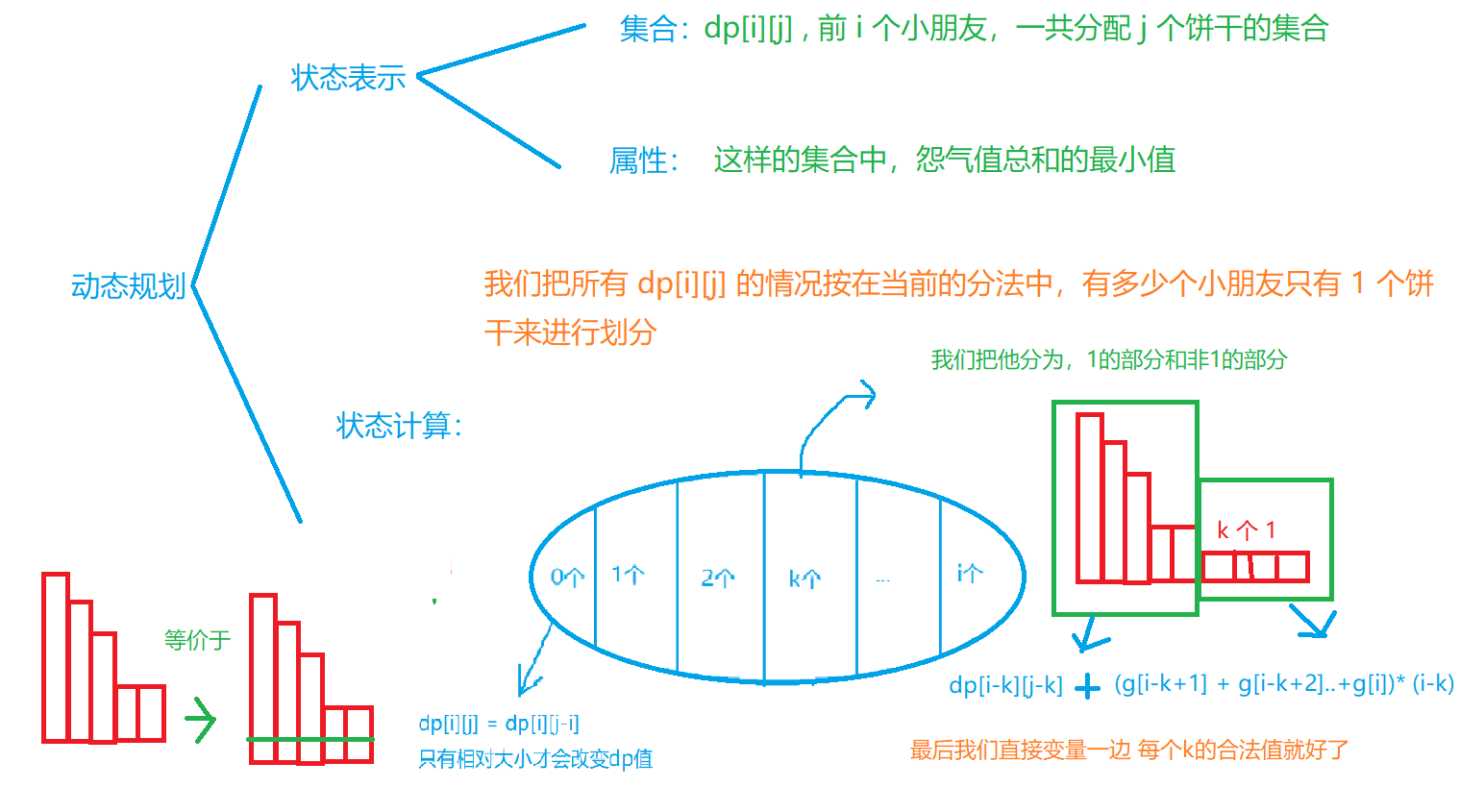
对于最后的路径打印,因为从后向前是递增的,所以我们利用这个递增的特性输出就可以了。
#include <bits/stdc++.h>
using namespace std;
const int N = 35,M = 5010;
pair<int, int> g[N];
int dp[N][M];
int sum[N];
int ans[N];
int main()
{
cin.tie(0)->sync_with_stdio(false);
int n, m; cin >> n >> m;
for (int i = 1; i <= n; i++) {
cin >> g[i].first; g[i].second = i;
}
sort(g + 1, g + 1 + n, greater<pair<int,int> >());
for (int i = 1; i <= n; i++)sum[i] = sum[i - 1] + g[i].first;
memset(dp, 0x3f, sizeof dp);
dp[0][0] = 0;
for (int i = 1; i <= n; i++) {
for (int j = i; j <= m; j++) {
if (j >= i) dp[i][j] = dp[i][j - i];
for (int k = 1; k <= i && k <= j ; k++) {
// 最后一个是 g[i-k+1] ,在求前缀和时 sum[i-k+1-1]抵消了
dp[i][j] = min(dp[i][j], dp[i - k][j - k] + (sum[i] - sum[i - k]) * (i - k));
}
}
}
cout << dp[n][m] << endl;
// h 是从后向前,递增的当前第 i 位分配了多少个饼干
int i = n, j = m,h = 0;
while (i) {
if (j >= i && dp[i][j] == dp[i][j - i]) j -= i, h++;
else {
for (int k = 1; k <= i && k <= j; k++) {
if (dp[i][j] == dp[i - k][j - k] + (sum[i] - sum[i - k]) * (i - k)) {
for (int u = i; u > i - k; u--) ans[g[u].second] = 1 + h;
i -= k, j -= k;
break;
}
}
}
}
for (int i = 1; i <= n; i++)cout << ans[i] << ' ';
cout << endl;
return 0;
}
6.2、背包
6.2.1、01背包
- 状态表示 (
dp[i][j])
- 集合: 在
1-i这些物品中,选出总体积为j的物品的集合- 属性:
w的最大值- 状态计算
- (
if (v[i] <= j)) 选第i个物品- 不选第
i个物品
#include <bits/stdc++.h>
using namespace std;
const int N = 1010;
int v[N], w[N];
int dp[N][N];
int main()
{
cin.tie(0)->sync_with_stdio(false);
int n, m; cin >> n >> m;
for (int i = 1; i <= n; i++)cin >> v[i] >> w[i];
for (int i = 1; i <= n; i++) {
for (int j = 1; j <= m; j++) {
// 不选第 i 个物品
dp[i][j] = dp[i - 1][j];
// 选第 i 个物品
if (v[i] <= j)dp[i][j] = max(dp[i][j], dp[i - 1][j - v[i]] + w[i]);
}
}
cout << dp[n][m] << endl;
return 0;
}
通过状态转移方程,我们发现,每一阶段 i 的状态只与上一阶段 i-1 的状态有关。所有我们可以使用 滚动数组 的方式来优化空间。
int dp[2][N];
int main()
{
cin.tie(0)->sync_with_stdio(false);
int n, m; cin >> n >> m;
for (int i = 1; i <= n; i++)cin >> v[i] >> w[i];
for (int i = 1; i <= n; i++) {
for (int j = 1; j <= m; j++) {
// 不选第 i 个物品
dp[i & 1][j] = dp[(i - 1) & 1][j];
// 选第 i 个物品
if (v[i] <= j) dp[i & 1][j] = max(dp[i & 1][j], dp[(i - 1) & 1][j - v[i]] + w[i]);
}
}
cout << dp[n&1][m] << endl;
return 0;
}
滚动数组的代码和原始的代码唯一的区别就是在 i 这一层加上了 &1 这个操作,那么就会根据奇偶性来调用当前一轮的数据和上一轮的数据。从而使得空间复杂度从 O(NM) 降低到了 O(M)
6.2.2、完全背包
7、图论
8、字符串
8.1、字符串的最小表示法
定义:对于一个字符串 S,求 S 的循环的同构字符串 s 中字典序最小的一个。(对于字符串 1234 他的循环同构字符串可以为 3412,2341)

对于数组的最小表示
void get_min(int *b)
{
const int len = 6; /// 数组长度
static int a[len<<1];
for (int i = 0; i < (len << 1); i++) a[i] = b[i % len];// 复制一份 b在b的后面,把这个结果赋值给 a
int i = 0, j = 1, k;
while (i < len && j < len) {
// k 表示的是当前比对的第几位
for (k = 0; k < len && a[i + k] == a[j + k]; k++); // 注意这里只移动指针
if (k == len) break;
// 上面的小于下面的
if (a[i + k] > a[j + k]) {
i += k + 1;
if (i == j) i++;
}
else {
j += k + 1;
if (i == j) j++;
}
}
k = min(i, j);
for (int i = 0; i < 6; i++)b[i] = a[i + k];
}
8.2、字符串 Hash
记忆时注意:
get中p[r-l]- 初始化
p[0] = Mod
typedef unsigned long long ull;
const int N = 1e5 + 10, Mod = 131;
ull h[N], p[N]; //h -> 从1-i 这个字符串的hash值,p -> Mod ^(i+1) 次方的值
char s[N];
inline ull get(int l, int r) { return h[r] - h[l - 1] * p[r - l]; }
signed main()
{
int n; cin >> n;
cin >> s;
h[0] = (ull)(s[0]); p[0] = Mod;
for (int i = 1; i < n; i++) {
h[i] = h[i - 1] * Mod + s[i];
p[i] = p[i - 1] * Mod;
}
}
9、计算几何
9.1、平面几何前置知识
///非科学计数法输出
cout.setf(ios::fixed);
///设置输出小数点
cout << setprecision(4) << x <<endl;
9.2、点
9.2.1、点的表示
在计算几何的题目中,基本上都是实数计算,所以我们一般都使用精度更高的 double 来进行计算。double 类型的数据在读入的时候要使用 %lf ,在输出的时候要使用 %f 。
struct Point
{
double x,y;
Point(){} /// 无参构造
Point(double _x,double _y):x(_x),y(_y){} /// 有参构造
}P[N];
9.2.2、两点之间的距离
两点距离公式: \(dis = \sqrt{(x_1-x_2)^2 + (y_1-y_2)^2}\)
double distance(Point P){
hypot(x-P.x,y-P.y); /// 库函数,求根号下,两数平方和
}
9.3、向量
9.3.1、计算机中的向量
我们一般表示一个向量也是直接用一个点来表示,方向是从原点指向(x,y)坐标
比如说 Point (4,2) 这个点就表示的是从原点指向 B 的一个向量,因为向量是可以平移的,所以为了方便计算,我们直接用一个点来表示一个向量。
在计算中的,我们处理区间的运算,多数是在坐标原点处理的,可能他真实的情况是 \((A_1,C_1)\) ,\((A_2,B_2)\) 这样的情况,但是我们都将其平移到原点处理
9.3.2、点积(Dot Product)
向量的基本运算是 点积 和 叉积 ,计算几何的各种操作几乎都基于这两种运算。
已知两个 \(\vec{a},\vec{b}\) 向量 ,它们的夹角为 \(\theta\) ,那么:$ a \cdot b = |a||b|\cos \theta $
就是这两个向量的 数量积,也叫 点积 或 内积 。点积的几何意义为: \(\vec{a}\) 在 \(\vec{b}\) 上的投影乘以 \(\vec{b}\) 的模长
9.3.2.1、向量间的投影
由点积公式:$ a \cdot b = |a||b|\cos \theta $
double operator * (Point b){
return x*b.x + y*b.y;
}
我们可以发现 \(|a|\cos \theta\) ,\(|b|\cos \theta\) 都为一个向量到另一个向量的投影。
我们就可以通过点积来计算相互之间的投影:
\(|b|\cos \theta = \frac{ \vec{a} \cdot \vec{b}}{|\vec{a}|}\)
\(|a|\cos \theta = \frac{ \vec{a} \cdot \vec{b}}{|\vec{b}|}\)
9.3.2.2、点积与\(cos \theta\)
夹角 \(\theta\) 与点积大小的关系:
(补充cos的图)
- 若 \(\theta = 0°\) ,\(\vec{a} \cdot \vec{b} = |\vec{a}||\vec{b}|\) ,同向共线
- 若 \(\theta = 180°\) ,\(\vec{a} \cdot \vec{b} = -|\vec{a}||\vec{b}|\) ,反向向共线
- 若 \(\theta = 90°\) ,\(\vec{a} \cdot \vec{b} = 0\) ,垂直
- 若 \(\theta < 90°\) ,\(\vec{a} \cdot \vec{b} > 0\) ,两向量的夹角为锐角
- 若 \(\theta > 90°\) ,\(\vec{a} \cdot \vec{b} < 0\) ,两向量的夹角为钝角
从上面我们可以发现,我们可以通过点积的结果来判断,共线的方向,以及垂直
9.3.3、叉积(Cross Product)
我们定义向量 \(\vec{a},\vec{b}\) 的向量积为一个向量,记为 \(\vec{a} \times \vec{b}\) ,其模与方向定义如下:
- \(|\vec{a} \times \vec{b}| = |\vec{a}||\vec{b}|\sin<a,b>\)
- \(\vec{a} \times \vec{b}\) 与 \(\vec{a},\vec{b}\) 都垂直,且 \(\vec{a} \times \vec{b} ,\vec{a},\vec{b}\) 都符合右手法则。
我的右手和官方的不太一样,平摊(正面或者反面朝上)右手,大拇指和第一个向量方向相同,四指指向另一个(如果别扭就翻过来)。
手心向上,大于零,手心向下,小于零。我觉得这样方便点。
向量积也叫外积,也叫叉积。
double operator ^ (Point b){
return x*b.y - y*b.x;
}
9.3.3.1、求平行四边形面积
然而注意到向量积的模,联想到三角形面积计算公式 \(S = \frac{1}{2}ab\sin{C}\) ,我们可以发现向量积的几何意义是: \(|\vec{a} \times \vec{b}|\) 是以为 $\vec{a},\vec{b} $ 为邻边的平行四边形的面积。
9.3.3.2、判断A,B向量方向关系
若 \(\vec{a} \times \vec{b} > 0\) ,\(\vec{b}\) 在 \(\vec{a}\) 的逆时针方向;
若 \(\vec{a} \times \vec{b} < 0\) ,\(\vec{b}\) 在 \(\vec{a}\) 的顺时针方向;
若 \(\vec{a} \times \vec{b} = 0\) , \(\vec{b}\) 与 \(\vec{a}\) 可能同向共线,也可能反向共线(刚才的点积就可以判断是同向共线还是反向共线),还可能平行。
9.3.4、向量的运算
9.3.4.1、向量模长
向量模长,就是原点到 (x,y) 坐标的距离(在我们的上述的建模方式下),对于向量 \(\vec{a}=(x,y)\) ,\(|\vec{a}|=\sqrt{(x-0)^2+(y-0)^2}\) ,所以我们用与求两点距离的方式来求向量的模长。
double len(){
return hypot(x,y);
}
/// 长度的平方,便于之后的计算
double len2(){
return x*x + y*y;
}
9.3.4.2、向量加、减
上图可以看到 \(\vec{AC}+\vec{AB}\) 的值就是坐标 \(D(C_x+B_x,C_y+B_y)\)
同时可以看到 \(\vec{AB}-\vec{AC}\) 的值就是坐标 \(\vec{CB}(B_x-C_x,B_y-C_y)\)
Point operator + (Point b){
return Point( x+b.x,y+b.y );
}
Point operator - (Point b){
return Point( x-b.x,y-b.y );
}
( 注:这些 operator 都是直接重载的结构体运算符,如果没有这方面的前置知识,请先学习如果重载结构体的运算符 )
9.3.4.3、向量数乘(放缩)
对于 \(\vec{a}=(x,y)\) ,\(\lambda \vec{a}=(\lambda x,\lambda y)\) ,除法的话等价于\(\frac{\vec{a}}{\lambda}=\frac{1}{\lambda}\vec{a}=(\frac{1}{\lambda} x,\frac{1}{\lambda} y)\)
Point operator * (double k){
return Point(k*x,k*y);
}
Point operator / (double k){
return Point(x/k , y/k);
}
对于数乘的具体应用是,把一个向量变为长度为 \(r\) 的向量,但是向量方向不变
Point trunc(double r){
double l = len();
r /= l;
return Point(x*r,y*r);
}
9.3.4.4、判断向量相等
因为计算机运行精度问题,所以我们不能直接用 == 来判断 double 类型的数据是否相等,这里引入,eps 来表示题目允许的误差范围,sgn 来代替比较运算符。
const double eps = 1e-8;
int sgn(double x)
{
if(fabs(x) < eps ) return 0;
if( x < 0 ) return -1;
else return 1;
}
1e-8 表示的是\(1\times 10^{-8}\) 是判断两值相等所允许的误差范围,比如 \(1.000000002\) 与 \(1.000000005\) 被视为相等的两个数,均表示 \(1.00000000\) ,如果两数相减的值,小于 eps 那么我们就视为这是两个相等的数,基于此,我们可重载 < ,== 运算符。小于运算符的排序规则是,x 小的,y 小的在前,x作为第一标准,y作为第二标准。
bool operator == (Point b) {
return sgn(x-b.x) == 0 && sgn(y-b.y) == 0;
}
bool operator < (Point b){
return sgn(x-b.x)==0?sgn(y-b.y)<0:b.x;
}
9.3.4.5、两向量夹角
前缀知识:
-
atan(x)表示求的是x的反正切,其返回值为\([-\frac{\pi}{2},+\frac{\pi}{2}]\)之间的一个数。 -
atan2(y,x)求的是y/x的反正切,其返回值为\([-\pi,+\pi]\)之间的一个数。
kuangbin用的方法是
double rad(Point a,Point b){
Point p = *this;
return fabs( atan2( fabs( (a-p)^(b-p) ) , (a-p)*(b-p) ) );
}
我看了一眼没有理解,就直接推了一遍,并测试了在精度为 esp=1e-10的情况下,两则的答案相同
我自己的公式推导:
对于两个从原点出发的向量
由点积公式可得: $x_1 y_1+x_2y_2 = |A|\cdot |B|\cdot \cos \theta $ ,由模长公式和反三角函数可得 \(\theta = \acos({\frac{x_1 y_1+x_2y_2}{\sqrt{x_1^2+y_1^2} \times \sqrt{x_2^2+y_2^2}} })\)
/// 求 a,b 向量对于原点的夹角
/// 如果是三个数的夹角的话,this 为中间的那个点,a,b为两端
/// return fabs( acos( ((a-tp)*(b-tp))/( (a-tp).len() * (b-tp).len() ) ) )
double rad(Point a,Point b){
Point tp = *this;
return fabs(acos( (tp*b)/(tp.len() * b.len()) ));
}
哦哦哦,我明白了,kuangbin的是这样推的,还是推荐用kuangbin的因为代码更加简介,我的推导只用了点积(之后会讲解),或者也可以只用叉积,但是如果我们把叉积与点积 相除,就会得到 kuangbin 的式子,下面为推导。
\(叉积:x_1 y_2-x_2y_1 = |A|\cdot |B|\cdot \sin \theta\)
\(点积:x_1 y_1+x_2y_2 = |A|\cdot |B|\cdot \cos \theta\) ,相除可得
$\frac{\sin \theta }{\cos \theta } = \frac{x_1 y_2-x_2y_1}{x_1 y_1+x_2y_2} $,进一步推导 \(\tan \theta = \frac{\vec{a} \cdot \vec{b} }{\vec{a} \times \vec{b} }\),然后求个反三角函数就好了,之后学习了点积和叉积的计算,同时我们重载了运算符之后,就会发现用这个方法来实现求夹角,代码就会比较精简。
kuangbin yyds!
9.3.4.6、向量旋转
设 \(\vec{a}=(x,y)\) ,倾角为 $\theta $ ,长度为 \(l = \sqrt{x^2+y^2}\) 。则 \(x=l\cos{\theta},y=l\sin{\theta}\) 。令其逆时针旋转 \(\alpha\) 度角,得到向量 \(\vec{b} = ( l\cos(\theta + \alpha),l\sin(\theta + \alpha) )\) 。
由三角恒等变换得,\(b = (l(\cos{\theta}\cos{\alpha}-\sin{\theta}\sin{\alpha}),(\sin{\theta}\sin{\alpha}+\cos{\theta}\sin{\alpha}))\)
将 \(x,y\) 的值带入式子得到,\(b=(x\cos{\alpha}-y\sin{\alpha},y\cos{\alpha}+x\sin{\alpha})\)
绕着 P 点旋转
Point rotata(Point p,double angle){
Point v = (*this) - p;
double c = cos(angle) , s = sin(angle);
return Point(p.x + v.x * c - v.y * s , p.y + v.x *s + v.y * c);
/// 绕原点旋转后,加上原来P点的偏移量
}
对于特殊的选择 90°,我们知道 \(\cos{90°}=0\) 所以就直接变成了
///逆时针旋转90度
Point rotleft(){
return Point(y,-x);
}
///顺时针旋转90度
Point rotright(){
return Point(y,-x);
}
9.3.5、向量板子
struct Point
{
double x,y;
double angle;
int id;
Point(){} /// 无参构造
Point(double _x,double _y){
x = _x; y = _y;
} /// 有参构造
/// 向量加法
Point operator + (const Point b) const{
return Point( x+b.x,y+b.y );
}
/// 向量乘法
Point operator - (const Point b) const{
return Point( x-b.x,y-b.y );
}
/// 向量数乘
Point operator * (const double k) const{
return Point(k*x,k*y);
}
/// 向量数除
Point operator / (const double k) const{
return Point(x/k , y/k);
}
bool operator == (const Point b) const{
return sgn(x-b.x) == 0 && sgn(y-b.y) == 0;
}
bool operator < (const Point b) const {
return sgn(x-b.x)==0?sgn(y-b.y)<0:x<b.x;
}
/// 点积
double operator * (const Point b) const{
return x*b.x + y*b.y;
}
/// 叉积
double operator ^ (const Point b) const{
return x*b.y - y*b.x;
}
/// 两点之间的距离
double distance(const Point P) const {
return hypot(x-P.x,y-P.y); /// 库函数,求根号下,两数平方和
}
/// 向量长度
double len(){
return hypot(x,y);
}
/// 长度的平方,便于之后的计算
double len2(){
return x*x + y*y;
}
/// 化为长度为 r 的向量
Point trunc(double r){
double l = len();
r /= l;
return Point(x*r,y*r);
}
/// 以 p 为中心点,pa,pb的夹角大小
double rad(Point a,Point b){
Point p = *this;
return fabs( atan2( fabs( (a-p)^(b-p) ) , (a-p)*(b-p) ) );
}
/// 绕 p点 逆时针选择 angle 度
Point rotate(Point p,double angle){
Point v = (*this) - p;
double c = cos(angle) , s = sin(angle);
return Point(p.x + v.x * c - v.y * s , p.y + v.x *s + v.y * c);
/// 绕原点旋转后,加上原来P点的偏移量
}
///逆时针旋转90度
Point rotleft(){
return Point(y,-x);
}
///顺时针旋转90度
Point rotright(){
return Point(y,-x);
}
};
9.4、点与直线
9.4.1、直线,线段的表示
在计算几何中,直线,线段我们都用两个 Point 来表示,如果把 Point 视为点的话,那么所组成的就是线段,如果把 Point 视为向量的话,那么所组成的就是直线。
struct Line
{
Point s,e;
Line(){}
Line(Point _s,Point _e):s(_s),e(_e){}
};
9.4.1.1、由解析式来表示直线
- 斜截式式 \(y=kx+b\)
- 标准方程 \(ax + by + c = 0\)
通常,我们采用斜截式的时候是用直线与 \(x\) 轴的顺时针倾斜角与直线上一点来得到两点。
我们设直线的斜倾角为 \(\theta\) ,斜率为 \(k\) ,已知两点 \(P_1(x_1,y_1),P_2(x_2,y_2)\)
\(k = \frac{y1-y2}{x1-x2}\) ,\(\tan{\theta}= \frac{y1-y2}{x1-x2}=k\) ,那么\(\theta = atan(k)\)。
Line(Point p,double angle){
s = p;
if( sgn(angle - pi/2) == 0 ) e = (s + Point(0,1));
else e = (s + Point(1,tan(angle)));
}
///ax + by + c = 0;
Line(double a,double b,double c){
if( sgn(a) == 0 ) {
s = Point(0,-c/b);
e = Point(1,-c/b);
}
else if(sgn(b) == 0) {
s = Point(-c/a,0);
e = Point(-c/a,1);
}
else {
s = Point(0,-c/b);
e = Point(1,(-c-a)/b);
}
}
9.4.1.2、线段长度
就是两点之间的距离
double length(){
return s.distance(e);
}
9.4.1.3、直线基于 x 轴的斜倾角
就是用 4.1.1 中的公式来求
注:
const doubel pi = acos(-1);
double angle(){
double k = atan2(e.y-s.y , e.x-s.x);
if( sgn(k) < 0 ) k += pi;
if( sgn(k-pi) == 0 ) k -=pi;
return k;
}
9.4.2、点与直线
9.4.2.1、点与直线的位置关系
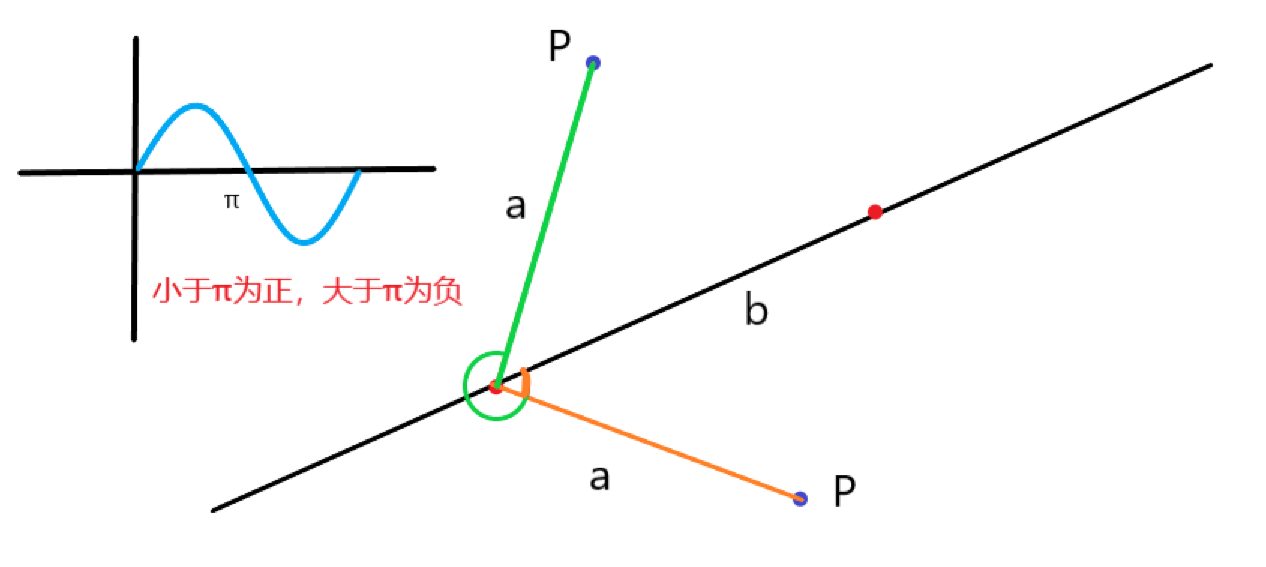
在二维平面上,点和直线有 3 种位置关系,点在直线左侧,点在直线右侧,点在直线上。记点为 \(P\),直线上的点为 \(P_1,P_2\) ,取 \(P_1P\),\(P_1P_2\) 构成向量用叉积就能得到位置关系。
///点与直线关系
///1在左侧
///2在右侧
///3在直线
int relation(Point p){
int c = sgn( (p-s) ^ (e -s) );
if(c < 0) return 1;
else if(c > 0) return 2;
else return 3;
}
9.4.2.2、点到直线的距离
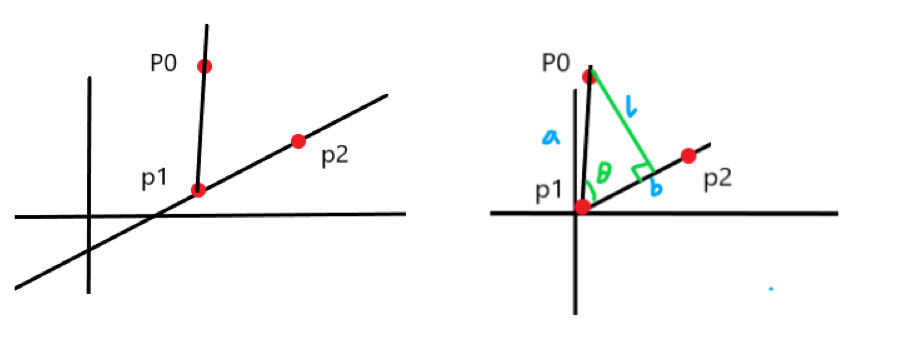
如图,我们设点 \(P_0\),取直线点 \(P_1,P_2\),我们用\(P_0-P_1,P_2-P_1\) 来将 \(P_1\) 点移动到原点,我们要求的点到直线的距离的长度设为 \(l\),\(P_0-P_1,P_2-P_1\) 两个向量的夹角设为 \(\theta\)。
通过叉积公式 \(\vec{a} \times \vec{b} = |\vec{a}||\vec{b}|\sin{\theta}\)
我们可以得到 \(|\vec{b}|\sin{\theta}= \frac{\vec{a} \times \vec{b}}{|\vec{a}|}=l\),这样我们就得到了点到直线的距离的计算公式,因为叉积是有正负的,所以最后要取个绝对值。
double dispointtoline(Point p){
return fabs( (p-s)^(e-s) ) / length();
}
9.4.2.3、点在直线上的投影(垂足)
还是上面哪个图,这次我们是要求 \(|\vec{b}|*\cos|\theta|\) , 我自己想的就是直接用点积来求,但是 kuangbin 和 黑书 都是用的成比例的方式,是因为求 cos 损失精度?需要 fabs ?
...
我去模拟了一下,才发现 lineProg 这个函数的返回值是 Point !!!所以这波是数学不过关。 我之前一直理解的是标量投影。但是这里我们求的是矢量投影,见百度百科。

设 \(P_0\) 到 \(P_1P_2\) 的垂足为 \(P_3\) (均为向量),为了计算不用cos 所以我们要求一个 \(k = \frac{|P_3-P_1|}{|P_2-P_1|}\) ,长度比例嘛, \(P_3\) 就是我们要求的 矢投影。
由点积的公式:$ (P_0-P_1) \cdot (P_2-P_1) = |P_0-P_1||P_2-P_1|\cos \theta $ ,我们把 \(P_3\) 引入
公式变为 : \((P_0-P_1) \cdot (P_2-P_1) = |P_2-P_1| * |P3-P_1|\)
带入 k 的式子中: $ k = \frac{|P_3-P_1|}{|P_2-P_1|}=\frac{(P_0-P_1) \cdot (P_2-P_1)}{|P_2-P_1| * |P_2-P_1|} $
所以,$P_3 = P_1 + k*(P_2-P_1) $
/// 返回点p在直线上的投影
Point lineprog(Point p){
return s + ( ( (e-s)*((e-s)*(p-s)) ) / ( (e-s).len2() ) );
}
这个也想相当于是,求点到直线的垂足向量。
9.4.2.4、点关于直线的对称点
求一个点对一条直线的对称点。先求点 \(P\) 在直线上的投影点 \(P_3\) (承接上一小节),再求对称点 。
就是把垂足的长度延长一倍就好了。
Point symmetrypoint(Point p){
Point q = lineprog(p);
return Point(2*q.x-p.x,2*q.y-p.y);
}
一组测试数据
int main() { Point p = Point(4,5); Line l = Line( Point(0,0),Point(1,10) ); Point te = l.lineprog(p) ; printf("%.10f\n%.10f\n",te.x,te.y); Point t = l.symmetrypoint(p); printf("%.10f\n%.10f",t.x,t.y); return 0; } /* 输出 0.5346534653 5.3465346535 -2.9306930693 5.6930693069 */
9.4.3、点与线段
9.4.3.1、点与线段的位置关系
判断点 \(p\) 是否在线段上, 先用叉积判断是共线,再判断是否与端点组成的线段与原线段形成钝角。
在 3.1.2 节,我们知道:
若 \(\theta = 180°\) ,\(\vec{a} \cdot \vec{b} = -|\vec{a}||\vec{b}|\) ,反向向共线
同时点 \(p\) 还有可能在端点上,所以最后为 \(\le 0\)
bool point_on_seg(Point p){
return sgn((p-s)^(e-s) ) == 0 && sgn( (p-s)*(p-e) ) <= 0 ;
}
9.4.3.2、点到线段的距离
点到线段的距离和点到直线的距离有所不同,设点为 \(P\) ,线段\(AB\) 。
在 P到AB的垂线长度,P到A的距离,P到B的距离,三者中取最小值。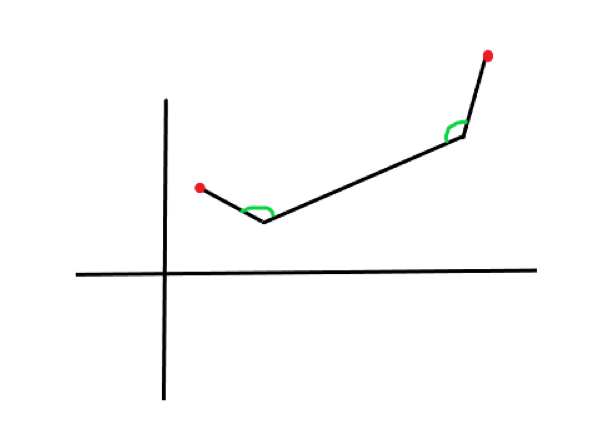
这是 if 判断的情况
double dispointtoseg(Point p){
if( sgn((p-s)*(e-s)) < 0 || sgn((p-e)*(s-e))<0 )
return min( p.distance(s),p.distance(e) );
return dispointtoline(p);
}
9.5、直线与线段
9.5.1、直线与直线的位置关系
9.5.1.1、判断直线与直线平行
在3.2.2小节,我们知道:
若 \(\vec{a} \times \vec{b} = 0\) , \(\vec{b}\) 与 \(\vec{a}\) 可能同向共线,也可能反向共线(刚才的点积就可以判断是同向共线还是反向共线),还可能平行。
bool parallel(Line v){
return sgn( (e-s)^(v.e-v.s) ) == 0 ;
}
9.5.1.2、两直线位置关系
思路就是,先判断平行,再判断是否共线,如果都不是的话那肯定是相交了。
这里共线我们直接用点与直线的共线来判断。
/// 判断两直线的位置关系
///0 平行
///1 共线
///2 相交
int linecrossline(Line v){
if( v.parallel(*this) ) return v.relation(s) == 3;
return 3;
}
9.5.2、直线与线段的位置关系
(-1)^(1) = 2
/// 直线与线段位置关系 -*this line -v seg
//2 规范相交
//1 非规范相交(顶点处相交)
//0 不相交
int linecrossseg(Line v){
int d1 = sgn( (e-s)^(v.s-s) );
int d2 = sgn( (e-s)^(v.e-s) );
if( (d1 ^ d2) == -2 ) return 2;
return (d1==0||d2==0);
}
9.5.3、线段与线段的位置关系
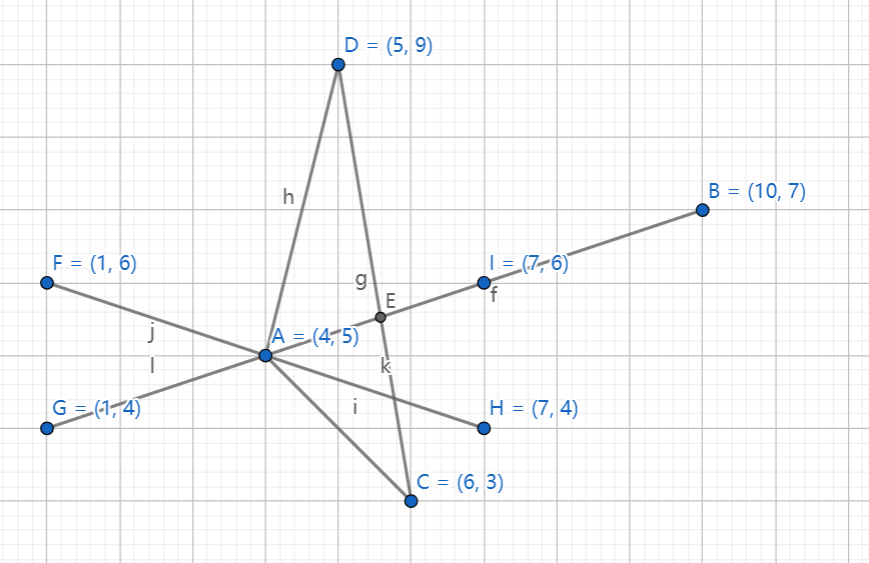
可用上图数据进行验证
///两线段相交判断
///2 规范相交
///1 非规范相交
///0 不想交
int segcrossseg(Line v) {
int d1 = sgn((e - s) ^ (v.s - s));
int d2 = sgn((e - s) ^ (v.e - s));
int d3 = sgn((v.e - v.s) ^ (s - v.s));
int d4 = sgn((v.e - v.s) ^ (e - v.s));
if ((d1 ^ d2) == -2 && (d3 ^ d4) == -2)return 2;
return (d1 == 0 && sgn((v.s - s) * (v.s - e)) <= 0) ||
(d2 == 0 && sgn((v.e - s) * (v.e - e)) <= 0) ||
(d3 == 0 && sgn((s - v.s) * (s - v.e)) <= 0) ||
(d4 == 0 && sgn((e - v.s) * (e - v.e)) <= 0);
}
9.5.4、线段到线段的距离
double disssegtoseg(Line v){
return min( { dispointtoseg(v.s),dispointtoseg(v.e) ,v.dispointtoseg(s), v.dispointtoseg(e) } );
}
直线到直线的距离,只有当两直线平行的时候才有意义,在两直线平行的情况下,我们直接随便取一个直线的 s,e 然后求点到直线的距离就可以了。
9.5.5、两条直线的交点
两直线,两线段的求交点是一样的,但是都要先判断是否相交,再求交点
Point crosspoint(Line v){
double a1 = (v.e-v.s)^(s-v.s);
double a2 = (v.e-v.s)^(e-v.s);
return Point( (s.x*a2-e.x*a1)/(a2-a1) , (s.y*a2-e.y*a1)/(a2-a1) );
}
9.6、线板子
struct Line
{
Point s,e;
Line(){}
Line(Point _s,Point _e){
s =_s; e= _e;
}
/// 点斜
Line(Point p,double angle){
s = p;
if( sgn(angle - pi/2) == 0 ) e = (s + Point(0,1));
else e = (s + Point(1,tan(angle)));
}
///ax + by + c = 0;
Line(double a,double b,double c){
if( sgn(a) == 0 ) {
s = Point(0,-c/b);
e = Point(1,-c/b);
}
else if(sgn(b) == 0) {
s = Point(-c/a,0);
e = Point(-c/a,1);
}
else {
s = Point(0,-c/b);
e = Point(1,(-c-a)/b);
}
}
/// 线段长度
double length(){
return s.distance(e);
}
/// 返回 0 <= angle <= pi 的基于 x轴 的斜倾角
double angle(){
double k = atan2(e.y-s.y , e.x-s.x);
if( sgn(k) < 0 ) k += pi;
if( sgn(k-pi) == 0 ) k -=pi;
return k;
}
///点与直线关系
//1 在左侧
//2 在右侧
//3 在直线
int relation(Point p){
int c = sgn( (p-s) ^ (e -s) );
if(c < 0) return 1;
else if(c > 0) return 2;
else return 3;
}
/// 点到直线的距离
double dispointtoline(Point p){
return fabs( (p-s)^(e-s) ) /length();
}
/// 返回点p在直线上的投影点(垂足)
Point lineprog(Point p){
return s + ( ( (e-s)*((e-s)*(p-s)) ) / ( (e-s).len2() ) );
}
/// 返回点p在直线上的对称点
Point symmetrypoint(Point p){
Point q = lineprog(p);
return Point(2*q.x-p.x,2*q.y-p.y);
}
/// 点与线段的位置关系
bool point_on_seg(Point p){
return sgn((p-s)^(e-s) ) == 0 && sgn( (p-s)*(p-e) ) <= 0 ;
}
/// 点到线段的距离
double dispointtoseg(Point p){
if( sgn((p-s)*(e-s)) < 0 || sgn((p-e)*(s-e))<0 )
return min( p.distance(s),p.distance(e) );
return dispointtoline(p);
}
/// 判断平行
bool parallel(Line v){
return sgn( (e-s)^(v.e-v.s) ) == 0 ;
}
/// 判断两直线的位置关系
//0 平行
//1 共线
//2 相交
int linecrossline(Line v){
if( v.parallel(*this) ) return v.relation(s) == 3;
return 3;
}
/// 直线与线段位置关系 -*this line -v seg
//2 规范相交
//1 非规范相交(顶点处相交)
//0 不相交
int linecrossseg(Line v){
int d1 = sgn( (e-s)^(v.s-s) );
int d2 = sgn( (e-s)^(v.e-s) );
if( (d1 ^ d2) == -2 ) return 2;
return (d1==0||d2==0);
}
///两线段相交判断
///2 规范相交
///1 非规范相交
///0 不想交
int segcrossseg(Line v) {
int d1 = sgn((e - s) ^ (v.s - s));
int d2 = sgn((e - s) ^ (v.e - s));
int d3 = sgn((v.e - v.s) ^ (s - v.s));
int d4 = sgn((v.e - v.s) ^ (e - v.s));
if ((d1 ^ d2) == -2 && (d3 ^ d4) == -2)return 2;
return (d1 == 0 && sgn((v.s - s) * (v.s - e)) <= 0) ||
(d2 == 0 && sgn((v.e - s) * (v.e - e)) <= 0) ||
(d3 == 0 && sgn((s - v.s) * (s - v.e)) <= 0) ||
(d4 == 0 && sgn((e - v.s) * (e - v.e)) <= 0);
}
/// 线段到线段的距离
double disssegtoseg(Line v){
return min( min( dispointtoseg(v.s),dispointtoseg(v.e)) , min(v.dispointtoseg(s), v.dispointtoseg(e) ) );
}
/// 求两直线的交点
Point crosspoint(Line v){
double a1 = (v.e-v.s)^(s-v.s);
double a2 = (v.e-v.s)^(e-v.s);
return Point( (s.x*a2-e.x*a1)/(a2-a1) , (s.y*a2-e.y*a1)/(a2-a1) );
}
};
9.6、多边形
之前的多数来自于
kuangbin计算几何板子,黑书,之后的可能就是我自己想的很多方法了
9.6.1、多边形的表示
maxp 为点的数量,狂兵的把求凸包,求极角排序都写在 struct 里面了,但是我觉得这个应该是在 点集上进行的操作,所以我写在了外面。
const int maxp = 1e5+10;
struct Polygon
{
int n;
Point p[maxp];
Line l[maxp];
/// 在多边形中添加点
void add(Point q){
p[n++] = q;
}
/// 获取所有的线段
void getLine(){
for(int i = 0; i < n ; i++){
l[i] = Line(p[i],p[(i+1)%n]);
}
}
};
9.6.2、多边形判定与求得
9.6.2.1、极角排序
对于一个二维平面上的点集,我们选择点集中,最左下角的点,做 J 点到 x轴 的平行线,为直线 JA,然后逆时针旋转 直线JA ,接触其他点的先后循序就是 极角排序 的结果。
如果有两个点与 JA 都相交,那么我们定义与 J 的距离短的优先级高。
- atan2得到极角排序
在 3.4.5 中我们知道了 atan 与 atan2 的区别,因为 atan2 的取值是在 \([-\pi,+\pi]\) 所以,我们用 atan2 来求,直线之间的夹角,因为极角排序其实就是夹角排序。
之前狂兵的板子中的
Point是没有angle属性的。我这里把极角排序从多边形中独立出来,多边形就只处理多边形那些关系,不管求凸包,极角排序这些,因为这些其实都是 点集 在干的事。
我调整了一下点的位置,把他们都变成了整数。
我先是这样写的 atan2 cmpAtan2Point 为最左下角的 J
te[i].angle = atan2( te[i].x - cmpAtan2Point.x,te[i].y - cmpAtan2Point.y );
然后我发现我是 x,y 写反了,最后他变成了 J与y轴平行,顺时针的过去!还有一个值得注意的问题:
\(atan2 \in [-\pi,+\pi]\) 所以,刚才的与
y轴平行的情况中B点的值为负,反而排到前面了,所以计算atan2的时候小于零的数都 \(+2π\) 。同时要注意,在
Point中,我们之前重载的<是x小就小x 的优先级比 y 高,这里我们需要提高 y 的优先级
修改的代码:
/// Point 的重载
bool operator < (Point b) const {
return sgn(y-b.y)==0?sgn(x-b.x)<0:y<b.y;
}
/// -------------------------------------------------///
/// 用来指定排序的极点
Point cmpAtan2Point = Point(inf,inf);
/// sort cmp
bool cmpAtan2(Point a,Point b)
{
if( sgn(a.angle - b.angle) == 0 ) return a.distance(cmpAtan2Point) < b.distance(cmpAtan2Point );
return a.angle < b.angle;
}
Point te[N];
int main()
{
te[0] = {6,10};
te[1] = {8,2};
te[2] = {10,6};
te[3] = {10,14};
te[4] = {12,4};
te[5] = {12,8};
te[6] = {16,12};
te[7] = {18,10};
te[8] = {18,8};
te[9] = {18,4};
te[10] = {6,8}; /// 我又加了一个,来验证负数的情况
/// 取到最小的数,所以需要重载运算符
for(int i = 0; i < 11 ; i++){
cmpAtan2Point = min(cmpAtan2Point,te[i]);
}
cout << cmpAtan2Point.x << ' ' << cmpAtan2Point.y << endl;
for(int i = 0; i < 11 ; i++){
if( te[i] == cmpAtan2Point ){
te[i].angle = 0;
}
else{
te[i].angle = atan2( te[i].x - cmpAtan2Point.x,te[i].y - cmpAtan2Point.y );
if( sgn(te[i].angle) < 0 ) te[i].angle += 2*pi;
}
}
sort(te,te+11,cmpAtan2);
for(int i = 0 ; i < 11 ; i++){
cout << te[i].angle <<endl;
cout <<te[i].x << ' ' << te[i].y <<endl;
}
return 0;
}
最后的结果:(注意这是 做J垂直于Y顺时针的极角排序)

修改为 J平行于X轴,逆时针扫
te[i].angle = atan2( te[i].y - cmpAtan2Point.y , te[i].x - cmpAtan2Point.x); ///只用修改这里
- 叉积得到极角排序
这个比较老火,主要是用来排序,以左下角为极点的。
bool cmpCross(const Point a,const Point b)
{
double d = sgn((a-cmpPoint)^(b-cmpPoint)) ;
if( d == 0 ) return sgn( a.distance(cmpPoint) - b.distance(cmpPoint) ) < 0;
return d > 0;
}
9.6.2.2、得到凸包
Gradham 扫描法的变种,Andrew 算法
///--------------------- 凸包 --------------------///
/// 求之前的点集
Point convexP[N];
int Sizep; /// 点集大小
void getconvex(Polygon &convex)
{
/// 按照 x 从小到大排序,如果 x 相同,按 y 排序。
sort(convexP,convexP+Sizep);
convex.n = Sizep;
for(int i = 0 ; i < min(Sizep,2) ; i ++){
convex.p[i] = convexP[i];
}
/// 特判
if( convex.n == 2 && ( convex.p[0] == convex.p[1] ) ) convex.n--;
if( Sizep <= 2 ) return ;
int &top = convex.n;
top = 1;
for(int i = 2; i < Sizep ; i++){
while( top && sgn( (convex.p[top] - convexP[i])^(convex.p[top-1]-convexP[i]) ) <= 0 ) top--;
convex.p[++top] = convexP[i];
}
int temp = top;
convex.p[++top] = convexP[Sizep-2];
for(int i = Sizep-3 ; i >= 0 ; i--){
while( top != temp && sgn( (convex.p[top] -convexP[i])^(convex.p[top-1]-convexP[i])) <= 0 ) top --;
convex.p[++top] = convexP[i];
}
if( convex.n == 2 && ( convex.p[0] == convex.p[1] ) ) convex.n--;
/// 这样求出来的顺时针的凸包,如果要逆时针的话,来一次极角排序就好了。
/// 极角排序
cmpPoint = convex.p[0];
sort(convex.p,convex.p+convex.n,cmpCross);
}
9.6.2.3、判定多边形是否为凸多边形
如果直接用点集来判断的话,要先求一波极角排序
bool isconvex(){
bool s[2];
memset(s,0,sizeof s);
for(int i = 0 ; i < n ; i++){
int j = (i+1)%n;
int k = (j+1)%n;
s[ sgn( (p[j]-p[i])^(p[k]-p[i]))+1 ] = true;
if( s[0] && s[2] ) return false;
}
return true;
}
9.6.3、多边形周长
double getcircumference(){
double sum = 0;
for(int i = 0 ; i < n ; i++){
sum += p[i].distance(p[(i+1)%n]);
}
return sum;
}
9.6.4、多边形面积
如果是凹多边形,要按顺序排列才行。凸多边形,跑一边极角。
double getarea(){
double sum = 0;
for(int i = 0; i < n ; i++){
sum += (p[i]^p[(i+1)%n]);
}
return fabs(sum)/2;
}
9.6.5、多边形的重心
对于面积切割的加权平均。三角形的顶点重量都是分均的,但是多边形就不是了,所以要面积分均才是真正的重心。下图的这个5边形的重心要向上移,而不是在中间。
Point getbarycenter(){
Point ret(0,0);
double area = 0 ;
for(int i = 1; i < n-1 ; i++){
double tmp = (p[i]-p[0])^(p[i+1]-p[0]);
if( sgn(tmp) == 0 ) continue;
area += tmp;
ret.x += (p[0].x + p[i].x + p[i+1].x)/3*tmp;
ret.y += (p[0].y + p[i].y + p[i+1].y)/3*tmp;
}
if( sgn(area)) ret = ret/area;
return ret;
}
9.6.6、点与多边形
9.6.6.1、点与多边形的位置关系
//3 点上
//2 边上
//1 内部
//0 外部
int relationpoint(Point q){
/// 在点上
for(int i = 0; i < n; i++){
if( p[i] == q ) return 3;
}
getLine(); /// 之前getline了的话,可以注释节约时间
/// 在边上
for(int i = 0; i < n ; i++){
if( l[i].point_on_seg(q) ) return 2;
}
/// 在内部
int cnt = 0;
for(int i = 0 ; i < n ; i++){
int j = (i+1)%n;
int k = sgn( (q-p[j])^(p[i]-p[j]) );
int u = sgn( p[i].y - q.y );
int v = sgn( p[j].y - q.y );
if( k > 0 && u < 0 && v >= 0 ) cnt ++;
if( k < 0 && v < 0 && u >= 0 ) cnt--;
}
return cnt != 0;
}
9.6.7、直线与多边形
-
判断线段 \(AB\) 是否在任意多边形 \(Poly\) 以内:不相交且两端点 \(A,B\) 均在多边形以内。
-
判断线段 \(AB\) 是否在凸多边形 \(Poly\) 以内:两端点 \(A,B\) 均在多边形以内。
9.6.8、多边形与多边形
判断任意两个多边形是否相离:属于不同多边形的任意两边都不相交 且 一个多边形上的任意点都不被另一个多边形所包含。
int relationpolygon(Polygon Poly){
getLine();
Poly.getLine();
for(int i1 = 0 ; i1 < n ; i1++){
int j1 = (i1+1)%n;
for(int i2 = 0 ; i2 <= Poly.n ; i2++){
int j2 = (i2+1)%Poly.n;
Line l1 = Line(p[i1],p[j1]);
Line l2 = Line(Poly.p[i2],Poly.p[j2]);
if( l1.segcrossseg(l2) ) return 0;
if( Poly.relationpoint(p[i1]) || relationpoint(Poly.p[i2]) ) return 0;
}
}
return 1;
}
9.6.5、多边形与圆
9.6.6、多边形板子
struct Polygon
{
int n;
Point p[maxp];
Line l[maxp];
/// 在多边形中添加点
void add(Point q){
p[n++] = q;
}
/// 获取所有的线段
void getLine(){
for(int i = 0; i < n ; i++){
l[i] = Line(p[i],p[(i+1)%n]);
}
}
/// 判断多边形是不是凸包
/// 如果是直接对点集效验的话,要先极角排序
bool isconvex(){
bool s[2];
memset(s,0,sizeof s);
for(int i = 0 ; i < n ; i++){
int j = (i+1)%n;
int k = (j+1)%n;
s[ sgn( (p[j]-p[i])^(p[k]-p[i]))+1 ] = true;
if( s[0] && s[2] ) return false;
}
return true;
}
/// 多边形周长
double getcircumference(){
double sum = 0;
for(int i = 0 ; i < n ; i++){
sum += p[i].distance(p[(i+1)%n]);
}
return sum;
}
/// 多边形面积
double getarea(){
double sum = 0;
for(int i = 0; i < n ; i++){
sum += (p[i]^p[(i+1)%n]);
}
return fabs(sum)/2;
}
/// 重心
Point getbarycenter(){
Point ret(0,0);
double area = 0 ;
for(int i = 1; i < n-1 ; i++){
double tmp = (p[i]-p[0])^(p[i+1]-p[0]);
if( sgn(tmp) == 0 ) continue;
area += tmp;
ret.x += (p[0].x + p[i].x + p[i+1].x)/3*tmp;
ret.y += (p[0].y + p[i].y + p[i+1].y)/3*tmp;
}
if( sgn(area)) ret = ret/area;
return ret;
}
/// 判断点与任意多边形的关系
//3 点上
//2 边上
//1 内部
//0 外部
int relationpoint(Point q){
/// 在点上
for(int i = 0; i < n; i++){
if( p[i] == q ) return 3;
}
// getLine(); /// 之前getline了的话,可以注释节约时间
/// 在边上
for(int i = 0; i < n ; i++){
if( l[i].point_on_seg(q) ) return 2;
}
/// 在内部
int cnt = 0;
for(int i = 0 ; i < n ; i++){
int j = (i+1)%n;
int k = sgn( (q-p[j])^(p[i]-p[j]) );
int u = sgn( p[i].y - q.y );
int v = sgn( p[j].y - q.y );
if( k > 0 && u < 0 && v >= 0 ) cnt ++;
if( k < 0 && v < 0 && u >= 0 ) cnt--;
}
return cnt != 0;
}
/// 判断多边形是否与多边形相离
int relationpolygon(Polygon Poly){
getLine();
Poly.getLine();
for(int i1 = 0 ; i1 < n ; i1++){
int j1 = (i1+1)%n;
for(int i2 = 0 ; i2 <= Poly.n ; i2++){
int j2 = (i2+1)%Poly.n;
Line l1 = Line(p[i1],p[j1]);
Line l2 = Line(Poly.p[i2],Poly.p[j2]);
if( l1.segcrossseg(l2) ) return 0;
if( Poly.relationpoint(p[i1]) || relationpoint(Poly.p[i2]) ) return 0;
}
}
return 1;
}
};
/// 用来指定排序的极点
Point cmpPoint = Point(inf,inf);
/// 需重载 Point 的小于符号
bool cmpAtan2(Point a,Point b)
{
if( sgn(a.angle - b.angle) == 0 ) return a.distance(cmpPoint) < b.distance(cmpPoint );
return a.angle < b.angle;
}
/// 慎用,第一个基本上就够了
bool cmpCross(const Point a,const Point b)
{
double d = sgn((a-cmpPoint)^(b-cmpPoint)) ;
if( d == 0 ) return sgn( a.distance(cmpPoint) - b.distance(cmpPoint) ) < 0;
return d > 0;
}
///--------------------- 凸包 --------------------///
/// 求之前的点集
Point convexP[N];
int Sizep; /// 点集大小
void getconvex(Polygon &convex)
{
/// 按照 x 从小到大排序,如果 x 相同,按 y 排序。
sort(convexP,convexP+Sizep);
convex.n = Sizep;
for(int i = 0 ; i < min(Sizep,2) ; i ++){
convex.p[i] = convexP[i];
}
/// 特判
if( convex.n == 2 && ( convex.p[0] == convex.p[1] ) ) convex.n--;
if( Sizep <= 2 ) return ;
int &top = convex.n;
top = 1;
for(int i = 2; i < Sizep ; i++){
while( top && sgn( (convex.p[top] - convexP[i])^(convex.p[top-1]-convexP[i]) ) <= 0 ) top--;
convex.p[++top] = convexP[i];
}
int temp = top;
convex.p[++top] = convexP[Sizep-2];
for(int i = Sizep-3 ; i >= 0 ; i--){
while( top != temp && sgn( (convex.p[top] -convexP[i])^(convex.p[top-1]-convexP[i])) <= 0 ) top --;
convex.p[++top] = convexP[i];
}
if( convex.n == 2 && ( convex.p[0] == convex.p[1] ) ) convex.n--;
/// 这样求出来的顺时针的凸包,如果要逆时针的话,来一次极角排序就好了。
/// 极角排序
// cmpPoint = convex.p[0];
// sort(convex.p,convex.p+convex.n,cmpCross);
}
9.7、圆
9.7.1、圆的表示
struct Circle
{
Point c;
double r;
Circle(){}
Circle(Point _c,double _r):c(_c),r(_r){}
Circle(double x,double y,double _r){ /// 点的坐标,圆心
c = Point(x,y); r = _r;
}
bool operator == (Circle v){
return (p == v.p) && sgn(r-v.r) == 0;
} /// 以圆心为主排序,半径为副排序
bool operator < (Circle v) const{
return ( (p<v.p) || (p == v.p) && sgn(r-v.r)<0 );
}
/// 面积
double area(){
return pi*r*r;
}
/// 周长
double circumference(){
return 2*pi*r;
}
};
9.7.2、点和圆的关系
/// 点和圆的位置关系
//0 圆外
//1 圆上
//2 圆内
int relationPoint(Point b){
double dst = b.distance(p);
if( sgn(dst-r)<0 ) return 2;
if( sgn(dst-r)==0 ) return 1;
return 0;
}
9.7.3、直线和圆的关系
9.7.3.1、直线和圆的位置关系
比较的是圆心到直线的距离和半径的关系
//0 圆外
//1 圆上
//2 园内
int relationLine(Line v){
double dst = v.dispointtoline(p);
if( sgn(dst-r) < 0 ) return 2;
if( sgn(dst-r) == 1 ) return 1;
return 0;
}
9.7.3.2、直线和圆的交点
9.7.4、线段和圆的关系
比较的是圆心到线段的距离和半径的关系
int relationSeg(Line v){
double d = p.dispointtoSeg(p);
if( sgn(dst-r) < 0 ) return 2;
if( sgn(dst-r) == 0 ) return 1;
return 0;
}
9.7.5、圆与圆的关系
9.7.5.1、圆与圆的位置关系
//5 相离
//4 外切
//3 相交
//2 内切
//1 内含
int relationcircle(Circle v){
double d = p.distance(v.p);
if( sgn( d-r-v.r ) > 0 ) return 5;
if( sgn( d-r-v.r ) == 0 ) return 4;
double l = fabs(r-v.r);
if( sgn( d-r-v.r ) < 0 && sgn(d-l) > 0 ) return 3;
if( sgn( d-l ) == 0 ) return 2;
if( sgn( d-l ) < 0 ) return 1;
}
9.7.5.2、圆与圆的交点个数
9.7.5.3、圆与圆的交点
9.7.5.4、两圆相交面积
9.7.6、直线和圆的交点
9.7.7、圆与三角形
9.7.7.1、三角形内接圆
9.7.7.2、三角形外接圆
9.7.7.3、圆与三角形相交面积
9.7.8、最小圆覆盖
9.8、专题
9.8.1、求凸包
9.6.2.2
9.8.2、最近点对
9.8.3、旋转卡壳
9.8.4、最远点对
9.8.4、半平面交
9.8.5、最小矩形覆盖
9.9、测试题
9.9.1、【LightOJ 1203】凸包+最小顶点夹角
9.9.2、【2020ICPC 昆明】线段与直线相交判断
这个题可以说是我计算几何的梦魇。今年上半年打昆明的时候,很快就发现了这个题是铜,但是到最后都没有过,今天知道原因了,没有排序的优先级有问题....
题意
给你一个点集,让你求任意一个点,与其他点所组成的直线与一条线段的第 k 个交点。保证没有3点共线。
题解
直接我们打个表,把所有的交点已经坐标都求出来,计算几何怎么搞都行,只要是基础的那些求交点,平行,都是\(O(1)\) 的世界复杂度。但是一定要对交点排序,排序的标准是距离线段第一个点的距离的长度!!。
还有就是,计算几何别用 cin !!! 计算几何别用 cin !!! 计算几何别用 cin !!!
#include <bits/stdc++.h>
using namespace std;
const double eps = 1e-8;
int sgn(double x)
{
if(fabs(x) < eps ) return 0;
if( x < 0 ) return -1;
else return 1;
}
const int N = 1e3+10;
const int pi = acos(-1);
//square of a double
inline double sqr(double x){return x*x;}
struct Point
{
double x,y;
Point(){} /// 无参构造
Point(double _x,double _y):x(_x),y(_y){} /// 有参构造
/// 向量加法
Point operator + (Point b){
return Point( x+b.x,y+b.y );
}
/// 向量乘法
Point operator - (Point b){
return Point( x-b.x,y-b.y );
}
/// 向量数乘
Point operator * (double k){
return Point(k*x,k*y);
}
/// 向量数除
Point operator / (double k){
return Point(x/k , y/k);
}
bool operator == (Point b) {
return sgn(x-b.x) == 0 && sgn(y-b.y) == 0;
}
bool operator < (Point b){
return sgn(x-b.x)==0?sgn(y-b.y)<0:b.x;
}
/// 点积
double operator * (Point b){
return x*b.x + y*b.y;
}
/// 叉积
double operator ^ (Point b){
return x*b.y - y*b.x;
}
/// 两点之间的距离
double distance(Point P){
return hypot(x-P.x,y-P.y); /// 库函数,求根号下,两数平方和
}
}P[N];
struct Line
{
Point s,e;
Line(){}
Line(Point _s,Point _e):s(_s),e(_e){}
/// 直线与线段位置关系 -*this line -v seg
//2 规范相交
//1 非规范相交(顶点处相交)
//0 不相交
int linecrossseg(Line v){
int d1 = sgn( (e-s)^(v.s-s) );
int d2 = sgn( (e-s)^(v.e-s) );
if( (d1 ^ d2) == -2 ) return 2;
return (d1==0||d2==0);
}
/// 求两直线的交点
Point crosspoint(Line v){
double a1 = (v.e-v.s)^(s-v.s);
double a2 = (v.e-v.s)^(e-v.s);
return Point( (s.x*a2-e.x*a1)/(a2-a1) , (s.y*a2-e.y*a1)/(a2-a1) );
}
};
double t1,t2,t3,t4;
vector<Point> ans[N];
bool cmp(Point a,Point b){
return a.distance(Point{t1,t2}) < b.distance(Point{t1,t2});
}
int main()
{
int n,m;
scanf("%d%d",&n,&m);
scanf("%lf%lf%lf%lf",&t1,&t2,&t3,&t4);
Line seg = Line(Point(t1,t2),Point(t3,t4));
for(int i = 1 ; i <= n ; i++){
scanf("%lf%lf",&P[i].x,&P[i].y);
}
for(int i = 1; i <= n ; i ++){
for(int j = 1; j <= n ; j++){
if(i ==j)continue;
Line tel = Line(P[i],P[j]);
if( tel.linecrossseg(seg) ){
Point tep = tel.crosspoint(seg);
ans[i].push_back(tep);
}
}
}
for(int i = 1 ; i <= n ; i++){
sort(ans[i].begin(),ans[i].end(),cmp);
}
while(m--){
int te1,te2;
scanf("%d%d",&te1,&te2);
if( ans[te1].size() < te2 ){
puts("-1");
continue;
}
printf("%.6f %.6f\n",ans[te1][te2-1].x,ans[te1][te2-1].y);
}
return 0;
}
9.9.3、【POJ - 2007】极角排序
#include <iostream>
#include <cmath>
#include <stdio.h>
#include <algorithm>
using namespace std;
const double eps = 1e-8;
const double inf = 1e14;
int sgn(double x)
{
if(fabs(x) < eps ) return 0;
if( x < 0 ) return -1;
else return 1;
}
struct Point
{
double x,y;
double angle;
Point(){} /// 无参构造
Point(double _x,double _y){
x = _x; y = _y;
} /// 有参构造
/// 向量加法
Point operator + (Point b) const{
return Point( x+b.x,y+b.y );
}
/// 向量乘法
Point operator - (Point b) const{
return Point( x-b.x,y-b.y );
}
bool operator == (Point b) const{
return sgn(x-b.x) == 0 && sgn(y-b.y) == 0;
}
bool operator < (Point b) const {
return sgn(x-b.x)==0?sgn(y-b.y)<0:x<b.x;
}
/// 叉积
double operator ^ (Point b) const{
return x*b.y - y*b.x;
}
}P;
/// 用来指定排序的极点
Point cmpPoint = Point(inf,inf);
bool cmpCross(const Point &a,const Point &b)
{
double d = (a-cmpPoint)^(b-cmpPoint) ;
// if( sgn(d) == 0 ) return sgn( a.distance(cmpPoint) - b.distance(cmpPoint) ) < 0;
return d >= 0;
}
Point te[100];
int main()
{
int it = 0;
while(scanf("%lf%lf",&te[it].x,&te[it].y) != EOF) ++it;
cmpPoint = Point(0,0);
sort(te+1,te+it,cmpCross);
for(int i = 0 ; i < it ; i++){
printf("(%.0f,%.0f)\n",te[i].x,te[i].y);
}
return 0;
}
/*
80 20
50 -60
0 0
70 -50
60 30
-30 -50
90 -20
-30 -40
-10 -60
90 10
*/
9.9.4、【CF 598C】极角排序
9.9.5、【LightOj 1203】 凸包 + 边夹角
#include <iostream>
#include <cmath>
#include <stdio.h>
#include <algorithm>
#include <vector>
using namespace std;
const double eps = 1e-18;
int sgn(double x)
{
if(fabs(x) < eps ) return 0;
if( x < 0 ) return -1;
else return 1;
}
const int N = 1e5+10;
const int maxp = 1e5+10;
const double pi = acos(-1);
const double inf = 1e14;
//square of a double
inline double sqr(double x){return x*x;}
/*
* Point ()
* distance(Point P) - distance from this to P
* len() - get the length from (0,0) to (x,y)
* trunc(double r) - transform to the vector which length is r
* rad(Point a)
*/
struct Point
{
double x,y;
double angle;
int id;
Point(){} /// 无参构造
Point(double _x,double _y){
x = _x; y = _y;
} /// 有参构造
Point operator + (const Point b) const{return Point( x+b.x,y+b.y );}
Point operator - (const Point b) const{return Point( x-b.x,y-b.y );}
/// 向量数乘
Point operator * (const double k) const{
return Point(k*x,k*y);
}
/// 向量数除
Point operator / (const double k) const{
return Point(x/k , y/k);
}
bool operator == (const Point b) const{
return sgn(x-b.x) == 0 && sgn(y-b.y) == 0;
}
bool operator < (const Point b) const {
return sgn(x-b.x)==0?sgn(y-b.y)<0:x<b.x;
}
/// 点积
double operator * (const Point b) const{
return x*b.x + y*b.y;
}
/// 叉积
double operator ^ (const Point b) const{
return x*b.y - y*b.x;
}
/// 两点之间的距离
double distance(const Point P) const {
return hypot(x-P.x,y-P.y); /// 库函数,求根号下,两数平方和
}
/// 向量长度
double len(){
return hypot(x,y);
}
/// 以 p 为中心点,pa,pb的夹角大小
double rad(Point a,Point b){
Point p = *this;
return fabs( atan2( fabs( (a-p)^(b-p) ) , (a-p)*(b-p) ) );
}
};
struct Polygon
{
int n;
Point p[maxp];
};
/// 用来指定排序的极点
Point cmpPoint = Point(inf,inf);
/// 慎用,第一个基本上就够了
bool cmpCross(const Point a,const Point b)
{
double d = sgn((a-cmpPoint)^(b-cmpPoint)) ;
if( d == 0 ) return sgn( a.distance(cmpPoint) - b.distance(cmpPoint) ) < 0;
return d > 0;
}
///--------------------- 凸包 --------------------///
/// 求之前的点集
Point convexP[N];
int Sizep; /// 点集大小
void getconvex(Polygon &convex)
{
/// 按照 x 从小到大排序,如果 x 相同,按 y 排序。
sort(convexP,convexP+Sizep);
convex.n = Sizep;
for(int i = 0 ; i < min(Sizep,2) ; i ++){
convex.p[i] = convexP[i];
}
/// 特判
if( convex.n == 2 && ( convex.p[0] == convex.p[1] ) ) convex.n--;
if( Sizep <= 2 ) return ;
int &top = convex.n;
top = 1;
for(int i = 2; i < Sizep ; i++){
while( top && sgn( (convex.p[top] - convexP[i])^(convex.p[top-1]-convexP[i]) ) <= 0 ) top--;
convex.p[++top] = convexP[i];
}
int temp = top;
convex.p[++top] = convexP[Sizep-2];
for(int i = Sizep-3 ; i >= 0 ; i--){
while( top != temp && sgn( (convex.p[top] -convexP[i])^(convex.p[top-1]-convexP[i])) <= 0 ) top --;
convex.p[++top] = convexP[i];
}
if( convex.n == 2 && ( convex.p[0] == convex.p[1] ) ) convex.n--;
}
Polygon poly;
void solve()
{
int n;
cin >> n;
Sizep = n;
for(int i = 0; i < n ; i++){
double tex,tey;
scanf("%lf%lf",&tex,&tey);
convexP[i] = Point(tex,tey);
}
if( n <= 2 ) {puts("0.000000");return ;}
getconvex(poly);
double ans_angle = 1e5;
for(int i = 0; i < poly.n ; i++){
int j = (i+1)%poly.n;
int k = (j+1)%poly.n;
// printf("%.2f %.2f %.2f\n",poly.p[j].x,poly.p[i].x,poly.p[k].x);
double te_angle = poly.p[j].rad(poly.p[i],poly.p[k]);
ans_angle = min(te_angle,ans_angle);
}
printf("%.6f\n",((ans_angle)*180.0)/pi) ;
return ;
}
int main()
{
int t;
scanf("%d",&t);
for(int i = 1; i <= t ; i++){
printf("Case %d: ",i);
solve();
}
}
/*
2
11
6 10
8 2
10 6
10 14
12 4
12 8
16 12
18 10
18 8
18 4
6 8
4
0 0
10 0
10 10
2 1
1
3
0 0
3 0
0 3
*/
9.10、kuangbin 计算几何板子
const double eps = 1e-8;
const double pi = acos( -1.0);
///Compares a double to zero
int sgn(double x)
{
if( fabs(x) < eps ) return 0;
if( x < 0 ) return -1;
else return 1;
}
///square of a double
inline double sqr(double x) { return x * x; }
/////////////////////////////////////////////////
struct Point
{
double x,y;
Point(){} ///no arguments constructor
Point(double _x,double _y) {
x = _x , y = _y; ///arguments constructor
}
/*void input(){
scanf("%lf%lf",&x,&y);
}
void output(){
printf("%.2f %.2f\n",x,y);
}*/
bool operator == (Point b) const{
return sgn(x - b.x) == 0 && sgn(y - b.y) == 0;
}
bool operator < (Point b) const{
return sgn(x - b.x) == 0? sgn(y - b.y) < 0 : x < b.x;
}
///数量积
Point operator - (const Point &b) const{
return Point(x - b.x , y - b.y);
}
Point operator + (const Point &b) const{
return Point(x + b.x , y + b.y);
}
Point operator * (const double &k) const{
return Point(x * k , y * k );
}
Point operator / (const double &k) const{
return Point(x / k , y / k);
}
///叉积
double operator ^ (const Point &b) const{
return x * b.y - y * b.x;
}
///点积
double operator * (const Point &b) const{
return x * b.x + y * b.y;
}
///线段的长度
double len(){
return hypot(x,y); ///<cmath>
}
///长度的平方
double len2(){
return x * x + y * y;
}
///返回两点的距离
double distance(Point p){
return hypot( x - p.x , y - p.y );
}
///计算 pa 和 pb 的夹角
double rad(Point a,Point b){
Point p = *this;
return fabs( atan2( fabs( (a-p)^(b-p) ) , (a-p)*(b-p) ) );
}
///化为长度为r的向量
Point trunc(double r){
double l = len();
if( !sgn(l) ) return *this;
r /= l;
return Point(-y,x);
}
///逆时针旋转90度
Point rotleft(){
return Point(y,-x);
}
///顺时针旋转90度
Point rotright(){
return Point(y,-x);
}
///绕着p点逆时针
Point rotata(Point p,double angle){
Point v = (*this) - p;
double c = cos(angle) , s = sin(angle);
return Point(p.x + v.x * c - v.y * s , p.y + v.x *s + v.y * c);
}
};
struct Line
{
Point s,e;
Line(){}
Line( Point _s, Point _e ){ s =_s ; e=_e; }
///由斜倾角angle与任意直线一点确定直线 y = kx + b;
void input( Point _s, Point _e ){ s =_s ; e=_e; }
Line(Point p,double angle){
s = p;
if( sgn(angle - pi/2) == 0 ) e = (s + Point(0,1));
else e = (s + Point(1,tan(angle)));
}
///ax + by + c = 0;
Line(double a,double b,double c){
if( sgn(a) == 0 )
{
s = Point(0,-c/b);
e = Point(1,-c/b);
}
else if(sgn(b) == 0)
{
s = Point(-c/a,0);
e = Point(-c/a,1);
}
else
{
s = Point(0,-c/b);
e = Point(1,(-c-a)/b);
}
}
double length(){ return s.distance(e);}
///直线与线段相交判断
///-*this line -v seg
///2规范相交,1非规范相交,0不相交
bool linecrossseg(Line v){
return sgn( (v.s - e) ^ (s - e) ) * sgn(( v.e-e ) ^ (s -e) ) <= 0;
}
///点与直线关系
///1在左侧
///2在右侧
///3在直线
int relation(Point p){
int c = sgn( (p-s) ^ (e -s) );
if(c < 0) return 1;
else if(c > 0) return 2;
else return 3;
}
///点在线段上的判断
bool point_on_seg(Point p){
return sgn((p-s)^(e-s) ) == 0 && sgn( (p-s)*(p-e) ) <= 0 ;
}
///两向量平行(对应直线平行或重合)
bool parallel(Line v){
return sgn( (e-s)^( v.e - v.s ) ) == 0;
}
///两直线关系 0-平行,1-重合,2-相交
int linecrossline(Line v){
if( (*this).parallel(v) )
return v.relation(s) == 3;
return 2;
}
///得到交点,需先判断直线是否相交
Point crosspoint(Line v){
double a1 = ( v.e - v.s ) ^ ( s - v.s );
double a2 = ( v.e - v.s ) ^ ( e - v.s );
return Point( (s.x * a2 - e.x * a1)/(a2 - a1) , (s.y *a2 - e.y *a1)/(a2 - a1));
}
///点到线段的距离
double dispointtoseg(Point p){
if( sgn( (p - s)*(e - s) < 0 ) || sgn( (p-e)*(s-e) ) < 0 )
return min( p.distance(s),p.distance(e) );
return dispointtoline(p);
}
/// 点到直线的距离
double dispointtoline(Point p){
return fabs( (p-s)^(e-s) ) / length();
}
/// 返回点p在直线上的投影
Point lineprog(Point p){
return s + ( ( (e-s)*((e-s)*(p-s)) ) / ( (e-s).len2() ) );
}
///两线段相交判断
///2 规范相交
///1 非规范相交
///0 不想交
int segcrossseg(Line v) {
int d1 = sgn((e - s) ^ (v.s - s));
int d2 = sgn((e - s) ^ (v.e - s));
int d3 = sgn((v.e - v.s) ^ (s - v.s));
int d4 = sgn((v.e - v.s) ^ (e - v.s));
if ((d1 ^ d2) == -2 && (d3 ^ d4) == -2)return 2;
return (d1 == 0 && sgn((v.s - s) * (v.s - e)) <= 0) ||
(d2 == 0 && sgn((v.e - s) * (v.e - e)) <= 0) ||
(d3 == 0 && sgn((s - v.s) * (s - v.e)) <= 0) ||
(d4 == 0 && sgn((e - v.s) * (e - v.e)) <= 0);
}
};
struct triangle
{
Point A,B,C;
Line a,b,c;
triangle(){}
triangle(Point _A,Point _B,Point _C){ A = _A ; B = _B ; C = _C;}
///求重心
Point incenter(){
return Point( ( A.x + B.x + C.x ) / 3, ( A.y + B.y + C.y ) / 3);
}
};
///已知三点求圆心与半径模板
void cal(int a,int b,int c)//求外心 ,外心为三角形三边的垂直平分线交点,
{
double a1 = p[b].x - p[a].x, b1 = p[b].y - p[a].y, c1 = (a1*a1 + b1*b1)/2;
double a2 = p[c].x - p[a].x, b2 = p[c].y - p[a].y, c2 = (a2*a2 + b2*b2)/2;
double d = a1 * b2 - a2 * b1;
x = p[a].x + (c1*b2 - c2*b1)/d,y = p[a].y + (a1*c2 - a2*c1)/d;
r = dis2(a);
}
struct circle{
Point p; ///圆心
double r; ///半径
circle(){}
circle( Point _p,double _r ) { p = _p ; r = _r; }
bool operator == (circle v){
return (p == v.p) && sgn(r - v.r) == 0;
}
bool operator < (circle v) const{
return ( (p<v.p) || (p == v.p) && sgn( r - v.r ) < 0 );
}
double area(){
return pi*r*r;
}
double circumference(){
return 2*pi*r;
}
/// 点与圆的关系
///0 在圆外
///1 在圆上
///2 在圆内
int relation(Point b)
{
double dst = b.distance(p);
if( sgn(dst - r) < 0 ) return 2;
else if( sgn(dst-r) == 0 ) return 1;
return 0;
}
///线段与园的关系
///比较的是圆心到线段的距离和半径的的关系
int relationseg(Line v){
double dst = v.dispointtoseg(p);
if( sgn(dst - r) < 0 ) return 2;
else if( sgn(dst - r) == 0 ) return 1;
return 0;
}
/// 直线和圆的关系
/// 比较的是圆心到直线的距离和半径的关系
int relationline(Line v){
double dst = v.dispointtoline(p);
if( sgn(dst - r) == 0 ) return 2;
else if( sgn( dst - r) == 0) return 1;
return 0;
}
/// 求直线和圆的交点个数
int pointcrossline(Line v,Point &p1,Point &p2){
if( !(*this).relationline(v) ) return 0;
Point a = v.lineprog(p);
double d = v.dispointtoline(p);
d = sqrt(r*r - d*d);
if( sgn(d) == 0 ){
p1 = a,p2 = a;
return 1;
}
p1 = a + (v.e - v.s).trunc(d);
p2 = a - (v.e - v.s).trunc(d);
return 2;
}
/// 求圆和三角形 pab 的相交面积
double areatriangle( Point a,Point b ){
if( sgn((p-a)^(p-b)) == 0 ) return 0.0;
Point q[5];
int len =0;
q[len++] = a;
Line l(a,b);
Point p1,p2;
if( pointcrossline( l,q[1],q[2] ) == 2 ){
if( sgn( ( a - q[1] )*( b - q[1] ) ) < 0 ) q[len ++] = q[1];
if( sgn( ( a - q[2] )*( b - q[2] ) ) < 0 ) q[len ++] = q[2];
}
q[len ++] = b;
if( len == 4 && sgn( (q[0]-q[1])*(q[2]-q[1]) ) > 0 ) swap( q[1],q[2] );
double res = 0;
for(int i = 0 ; i < len - 1; i++){
if( relation(q[i]) == 0 || relation( q[i + 1] ) == 0 ){
double arg = p.rad( q[i],q[i + 1] );
res += r*r*arg/2.0;
}
else{
res += fabs( (q[i] - p) ^ ( q[i+ 1] - p ) ) / 2.0;
}
}
return res;
}
};
const int maxp = 1100;
const int maxl = 2200;
struct polygon
{
int n; ///点的数量
Point p[maxp];
Line l[maxl];
struct cmp{
Point p;
cmp(const Point &p0){ p = p0;}
bool operator()( const Point &aa ,const Point &bb){
Point a = aa,b = bb;
int d = sgn( (a-p)^(b-p) );
if(d == 0) return sgn( a.distance(p) - b.distance(p)) < 0;
return d > 0;
}
};
///极角排序
///mi为最左下角的点
void norm(){
Point mi = p[0];
for(int i = 1; i < n; i ++) mi = min(mi,p[i]);
sort(p, p + n, cmp(mi) );
}
/// 判断任意点与多边形的关系
/// 3在顶点上
/// 2在边上
/// 1在内部
/// 0在外面
int relationpoint(Point tep)
{
for(int i = 0 ; i < n ; i++){
if( p[i] == tep ) return 3;
}
for(int i = 0 ; i < n; i++){
if( l[i].point_on_seg(tep) ) return 2;
}
int tecnt = 0;
for(int i = 0 ; i < n ; i++)
{
int j = (i + 1) % n;
int c = sgn( (tep - p[j]) ^ (p[i] - p[j]) );
int u = sgn( p[i].y - tep.y );
int v = sgn( p[j].y - tep.y );
if( c > 0 && u < 0 && v >=0 ) tecnt ++;
if( c < 0 && u >= 0 && v < 0 ) tecnt --;
}
return tecnt != 0;
}
/// 得到凸包
/// 得到的凸包里的点编号是 0 ~ n-1 的
void getconvex(polygon &convex)
{
sort(p , p + n);
convex.n = n;
for(int i = 0 ; i < min(n,2) ; i++){
convex.p[i] = p[i];
}
///特判
if( convex.n == 2 && (convex.p[0] == convex.p[1]) ) convex.n--;
if( n <= 2) return;
int &top = convex.n;
top = 1;
for(int i = 2; i < n ; i++){
while(top && sgn( (convex.p[top] - p[i]) ^ (convex.p[top-1] - p[i])) <= 0 ) top --;
convex.p[++top] = p[i];
}
int temp = top;
convex.p[++top] = p[n-2];
for(int i = n - 3; i >=0 ; i--)
{
while( top!=temp && sgn( (convex.p[top] - p[i]) ^ (convex.p[top-1] - p[i]) ) <=0 ) top--;
convex.p[++top] = p[i];
}
if( convex.n == 2&& ( convex.p[0] == convex.p[1]) ) convex.n --; ///特判
convex.norm();///得到的是顺时针的点,排序后逆时针
}
///判断是不是凸多边形,用点集,不是得到凸包之后的多边形
bool isconvex(){
bool s[2];
memset(s,false,sizeof(s));
for(int i = 0 ; i < n ; i++){
int j = (i + 1) % n;
int k = (j + 1) % n;
s[ sgn((p[j] - p[i]) ^ (p[k]-p[i]) ) + 1] =true;
if( s[0] && s[2]) return false;
}
return true;
}
///得到周长
double getcircumference(){
double sum = 0;
for(int i = 0 ; i < n ; i++){
sum += p[i].distance( p[(i + 1)%n] );
}
return sum;
}
///得到面积
double getarea()
{
double sum = 0;
for(int i = 0; i < n ; i++){
sum += ( p[i]^p[ (i+1)%n ] );
}
return fabs(sum)/2;
}
///得到重心
Point getbarycentre(){
Point ret(0,0);
double area = 0;
for(int i = 1; i < n - 1; i ++){
double tmp = ( p[i] - p[0] ) ^ (p[i + 1] - p[0]);
if( sgn(tmp) == 0 ) continue;
area += tmp;
ret.x += ( p[0].x + p[i].x + p[i + 1].x ) / 3 * tmp;
ret.y += ( p[0].y + p[i].y + p[i + 1].y ) / 3 * tmp;
}
if( sgn(area) ) ret = ret / area;
return ret;
}
///多边形和园交的面积
double areacircle(circle c){
double ans = 0;
for(int i = 0; i < n ; i++)
{
int j = (i + 1) %n;
if( sgn( (p[j] - c.p) ^ ( p[i] - c.p )) >= 0 )
ans += c.areatriangle( p[i],p[j] );
else ans -= c.areatriangle( p[i],p[j] );
}
return fabs(ans);
}
///多边形和圆的关系
/// 2圆完全在多边形内
/// 1圆在多边形里面,碰到了多边形边界
/// 0其他
int relationcircle(circle c){
int x = 2;
if( relationpoint(c.p) != 1 ) return 0; ///圆心不在内部
for(int i = 0; i < n ; i++){
if( c.relationseg(l[i] ) == 2 ) return 0;
if( c.relationseg(l[i] ) == 1 ) x = 1;
}
return x;
}
};
9.11、Hoppz 计算几何板子
#include <iostream>
#include <cmath>
#include <stdio.h>
#include <algorithm>
#include <vector>
#include <cstring>
using namespace std;
const double eps = 1e-18;
int sgn(double x)
{
if(fabs(x) < eps ) return 0;
if( x < 0 ) return -1;
else return 1;
}
const int N = 1e5+10;
const int maxp = 10;
const double pi = acos(-1);
const double inf = 1e14;
//square of a double
inline double sqr(double x){return x*x;}
/*
* Point ()
* distance(Point P) - distance from this to P
* len() - get the length from (0,0) to (x,y)
* trunc(double r) - transform to the vector which length is r
* rad(Point a)
*/
struct Point
{
double x,y;
double angle;
int id;
Point(){} /// 无参构造
Point(double _x,double _y){
x = _x; y = _y;
} /// 有参构造
/// 向量加法
Point operator + (const Point b) const{
return Point( x+b.x,y+b.y );
}
/// 向量乘法
Point operator - (const Point b) const{
return Point( x-b.x,y-b.y );
}
/// 向量数乘
Point operator * (const double k) const{
return Point(k*x,k*y);
}
/// 向量数除
Point operator / (const double k) const{
return Point(x/k , y/k);
}
bool operator == (const Point b) const{
return sgn(x-b.x) == 0 && sgn(y-b.y) == 0;
}
bool operator < (const Point b) const {
return sgn(x-b.x)==0?sgn(y-b.y)<0:x<b.x;
}
/// 点积
double operator * (const Point b) const{
return x*b.x + y*b.y;
}
/// 叉积
double operator ^ (const Point b) const{
return x*b.y - y*b.x;
}
/// 两点之间的距离
double distance(const Point P) const {
return hypot(x-P.x,y-P.y); /// 库函数,求根号下,两数平方和
}
/// 向量长度
double len(){
return hypot(x,y);
}
/// 长度的平方,便于之后的计算
double len2(){
return x*x + y*y;
}
/// 化为长度为 r 的向量
Point trunc(double r){
double l = len();
r /= l;
return Point(x*r,y*r);
}
/// 以 p 为中心点,pa,pb的夹角大小
double rad(Point a,Point b){
Point p = *this;
return fabs( atan2( fabs( (a-p)^(b-p) ) , (a-p)*(b-p) ) );
}
/// 绕 p点 逆时针选择 angle 度
Point rotate(Point p,double angle){
Point v = (*this) - p;
double c = cos(angle) , s = sin(angle);
return Point(p.x + v.x * c - v.y * s , p.y + v.x *s + v.y * c);
/// 绕原点旋转后,加上原来P点的偏移量
}
///逆时针旋转90度
Point rotleft(){
return Point(y,-x);
}
///顺时针旋转90度
Point rotright(){
return Point(y,-x);
}
};
struct Line
{
Point s,e;
Line(){}
Line(Point _s,Point _e){
s =_s; e= _e;
}
/// 点斜
Line(Point p,double angle){
s = p;
if( sgn(angle - pi/2) == 0 ) e = (s + Point(0,1));
else e = (s + Point(1,tan(angle)));
}
///ax + by + c = 0;
Line(double a,double b,double c){
if( sgn(a) == 0 ) {
s = Point(0,-c/b);
e = Point(1,-c/b);
}
else if(sgn(b) == 0) {
s = Point(-c/a,0);
e = Point(-c/a,1);
}
else {
s = Point(0,-c/b);
e = Point(1,(-c-a)/b);
}
}
/// 线段长度
double length(){
return s.distance(e);
}
/// 返回 0 <= angle <= pi 的基于 x轴 的斜倾角
double angle(){
double k = atan2(e.y-s.y , e.x-s.x);
if( sgn(k) < 0 ) k += pi;
if( sgn(k-pi) == 0 ) k -=pi;
return k;
}
///点与直线关系
//1 在左侧
//2 在右侧
//3 在直线
int relation(Point p){
int c = sgn( (p-s) ^ (e -s) );
if(c < 0) return 1;
else if(c > 0) return 2;
else return 3;
}
/// 点到直线的距离
double dispointtoline(Point p){
return fabs( (p-s)^(e-s) ) /length();
}
/// 返回点p在直线上的投影点(垂足)
Point lineprog(Point p){
return s + ( ( (e-s)*((e-s)*(p-s)) ) / ( (e-s).len2() ) );
}
/// 返回点p在直线上的对称点
Point symmetrypoint(Point p){
Point q = lineprog(p);
return Point(2*q.x-p.x,2*q.y-p.y);
}
/// 点与线段的位置关系
bool point_on_seg(Point p){
return sgn((p-s)^(e-s) ) == 0 && sgn( (p-s)*(p-e) ) <= 0 ;
}
/// 点到线段的距离
double dispointtoseg(Point p){
if( sgn((p-s)*(e-s)) < 0 || sgn((p-e)*(s-e))<0 )
return min( p.distance(s),p.distance(e) );
return dispointtoline(p);
}
/// 判断平行
bool parallel(Line v){
return sgn( (e-s)^(v.e-v.s) ) == 0 ;
}
/// 判断两直线的位置关系
//0 平行
//1 共线
//2 相交
int linecrossline(Line v){
if( v.parallel(*this) ) return v.relation(s) == 3;
return 3;
}
/// 直线与线段位置关系 -*this line -v seg
//2 规范相交
//1 非规范相交(顶点处相交)
//0 不相交
int linecrossseg(Line v){
int d1 = sgn( (e-s)^(v.s-s) );
int d2 = sgn( (e-s)^(v.e-s) );
if( (d1 ^ d2) == -2 ) return 2;
return (d1==0||d2==0);
}
///两线段相交判断
///2 规范相交
///1 非规范相交
///0 不想交
int segcrossseg(Line v) {
int d1 = sgn((e - s) ^ (v.s - s));
int d2 = sgn((e - s) ^ (v.e - s));
int d3 = sgn((v.e - v.s) ^ (s - v.s));
int d4 = sgn((v.e - v.s) ^ (e - v.s));
if ((d1 ^ d2) == -2 && (d3 ^ d4) == -2)return 2;
return (d1 == 0 && sgn((v.s - s) * (v.s - e)) <= 0) ||
(d2 == 0 && sgn((v.e - s) * (v.e - e)) <= 0) ||
(d3 == 0 && sgn((s - v.s) * (s - v.e)) <= 0) ||
(d4 == 0 && sgn((e - v.s) * (e - v.e)) <= 0);
}
/// 线段到线段的距离
double disssegtoseg(Line v){
return min( min( dispointtoseg(v.s),dispointtoseg(v.e)) , min(v.dispointtoseg(s), v.dispointtoseg(e) ) );
}
/// 求两直线的交点
Point crosspoint(Line v){
double a1 = (v.e-v.s)^(s-v.s);
double a2 = (v.e-v.s)^(e-v.s);
return Point( (s.x*a2-e.x*a1)/(a2-a1) , (s.y*a2-e.y*a1)/(a2-a1) );
}
};
struct Polygon
{
int n;
Point p[maxp];
Line l[maxp];
/// 在多边形中添加点
void add(Point q){
p[n++] = q;
}
/// 获取所有的线段
void getLine(){
for(int i = 0; i < n ; i++){
l[i] = Line(p[i],p[(i+1)%n]);
}
}
/// 判断多边形是不是凸包
/// 如果是直接对点集效验的话,要先极角排序
bool isconvex(){
bool s[2];
memset(s,0,sizeof s);
for(int i = 0 ; i < n ; i++){
int j = (i+1)%n;
int k = (j+1)%n;
s[ sgn( (p[j]-p[i])^(p[k]-p[i]))+1 ] = true;
if( s[0] && s[2] ) return false;
}
return true;
}
/// 多边形周长
double getcircumference(){
double sum = 0;
for(int i = 0 ; i < n ; i++){
sum += p[i].distance(p[(i+1)%n]);
}
return sum;
}
/// 多边形面积
double getarea(){
double sum = 0;
for(int i = 0; i < n ; i++){
sum += (p[i]^p[(i+1)%n]);
}
return fabs(sum)/2;
}
/// 重心
Point getbarycenter(){
Point ret(0,0);
double area = 0 ;
for(int i = 1; i < n-1 ; i++){
double tmp = (p[i]-p[0])^(p[i+1]-p[0]);
if( sgn(tmp) == 0 ) continue;
area += tmp;
ret.x += (p[0].x + p[i].x + p[i+1].x)/3*tmp;
ret.y += (p[0].y + p[i].y + p[i+1].y)/3*tmp;
}
if( sgn(area)) ret = ret/area;
return ret;
}
/// 判断点与任意多边形的关系
//3 点上
//2 边上
//1 内部
//0 外部
int relationpoint(Point q){
/// 在点上
for(int i = 0; i < n; i++){
if( p[i] == q ) return 3;
}
// getLine(); /// 之前getline了的话,可以注释节约时间
/// 在边上
for(int i = 0; i < n ; i++){
if( l[i].point_on_seg(q) ) return 2;
}
/// 在内部
int cnt = 0;
for(int i = 0 ; i < n ; i++){
int j = (i+1)%n;
int k = sgn( (q-p[j])^(p[i]-p[j]) );
int u = sgn( p[i].y - q.y );
int v = sgn( p[j].y - q.y );
if( k > 0 && u < 0 && v >= 0 ) cnt ++;
if( k < 0 && v < 0 && u >= 0 ) cnt--;
}
return cnt != 0;
}
/// 判断多边形是否与多边形相离
int relationpolygon(Polygon Poly){
getLine();
Poly.getLine();
for(int i1 = 0 ; i1 < n ; i1++){
int j1 = (i1+1)%n;
for(int i2 = 0 ; i2 <= Poly.n ; i2++){
int j2 = (i2+1)%Poly.n;
Line l1 = Line(p[i1],p[j1]);
Line l2 = Line(Poly.p[i2],Poly.p[j2]);
if( l1.segcrossseg(l2) ) return 0;
if( Poly.relationpoint(p[i1]) || relationpoint(Poly.p[i2]) ) return 0;
}
}
return 1;
}
};
struct Circle
{
Point p;
double r;
Circle(){}
Circle(Point _p,double _r):p(_p),r(_r){}
Circle(double x,double y,double _r){ /// 点的坐标,圆心
p = Point(x,y); r = _r;
}
bool operator == (Circle v){
return (p == v.p) && sgn(r-v.r) == 0;
} /// 以圆心为主排序,半径为副排序
bool operator < (Circle v) const{
return ( (p<v.p) || (p == v.p) && sgn(r-v.r)<0 );
}
/// 面积
double area(){
return pi*r*r;
}
/// 周长
double circumference(){
return 2*pi*r;
}
/// 点和圆的位置关系
//0 圆外
//1 圆上
//2 圆内
int relationPoint(Point b){
double dst = b.distance(p);
if( sgn(dst-r)<0 ) return 2;
if( sgn(dst-r)==0 ) return 1;
return 0;
}
/// 直线和圆的关系
//0 相离
//1 相切
//2 相交
int relationLine(Line v){
double dst = v.dispointtoline(p);
if( sgn(dst-r) < 0 ) return 2;
if( sgn(dst-r) == 0 ) return 1;
return 0;
}
/// 线段和圆的关系
int relationSeg(Line v){
double dst = v.dispointtoseg(p);
if( sgn(dst-r) < 0 ) return 2;
if( sgn(dst-r) == 0 ) return 1;
return 0;
}
/// 两圆的关系
//5 相离
//4 外切
//3 相交
//2 内切
//1 内含
int relationcircle(Circle v){
double d = p.distance(v.p);
if( sgn( d-r-v.r ) > 0 ) return 5;
if( sgn( d-r-v.r ) == 0 ) return 4;
double l = fabs(r-v.r);
if( sgn( d-r-v.r ) < 0 && sgn(d-l) > 0 ) return 3;
if( sgn( d-l ) == 0 ) return 2;
if( sgn( d-l ) < 0 ) return 1;
}
};
/// 用来指定排序的极点
Point cmpPoint = Point(inf,inf);
/// 需重载 Point 的小于符号
bool cmpAtan2(Point a,Point b)
{
if( sgn(a.angle - b.angle) == 0 ) return a.distance(cmpPoint) < b.distance(cmpPoint );
return a.angle < b.angle;
}
/// 慎用,第一个基本上就够了
bool cmpCross(const Point a,const Point b)
{
double d = sgn((a-cmpPoint)^(b-cmpPoint)) ;
if( d == 0 ) return sgn( a.distance(cmpPoint) - b.distance(cmpPoint) ) < 0;
return d > 0;
}
///--------------------- 凸包 --------------------///
/// 求之前的点集
Point convexP[N];
int Sizep; /// 点集大小
void getconvex(Polygon &convex)
{
/// 按照 x 从小到大排序,如果 x 相同,按 y 排序。
sort(convexP,convexP+Sizep);
convex.n = Sizep;
for(int i = 0 ; i < min(Sizep,2) ; i ++){
convex.p[i] = convexP[i];
}
/// 特判
if( convex.n == 2 && ( convex.p[0] == convex.p[1] ) ) convex.n--;
if( Sizep <= 2 ) return ;
int &top = convex.n;
top = 1;
for(int i = 2; i < Sizep ; i++){
while( top && sgn( (convex.p[top] - convexP[i])^(convex.p[top-1]-convexP[i]) ) <= 0 ) top--;
convex.p[++top] = convexP[i];
}
int temp = top;
convex.p[++top] = convexP[Sizep-2];
for(int i = Sizep-3 ; i >= 0 ; i--){
while( top != temp && sgn( (convex.p[top] -convexP[i])^(convex.p[top-1]-convexP[i])) <= 0 ) top --;
convex.p[++top] = convexP[i];
}
if( convex.n == 2 && ( convex.p[0] == convex.p[1] ) ) convex.n--;
/// 这样求出来的顺时针的凸包,如果要逆时针的话,来一次极角排序就好了。
/// 极角排序
// cmpPoint = convex.p[0];
// sort(convex.p,convex.p+convex.n,cmpCross);
}
最小圆覆盖
inline int PIC(Circle C,Point a){return dcmp(Len(a-C.O)-C.r)<=0;}//判断点A是否在圆C内
inline Circle Min_Circle(Point *P,Re n){//【求点集P的最小覆盖圆】
// random_shuffle(P+1,P+n+1);
for(int i = 0 ; i < n ; i++) swap(P[i],P[rand()%n+1]);
Circle C=Circle(P[0],0);
for(int i=1;i<n;++i)if(!C.relationPoint(P[i])){
C=Circle(P[i],0);
for(Rinte j=1;j<i;++j)if(!C.relationPoint(P[j])){
C.p=(P[i]+P[j])*0.5,C.r=P[j].distance(C.p);
for(int k=1;k<j;++k)if(!C.relationPoint(P[j]))C=getcircle(P[i],P[j],P[k]);
}
}
return C;
}
10、经典模型
10.1、括号匹配问题
合法括号序列:
- 左括号数 == 右括号数
- 在所有的前缀中 左括号数 >= 右括号数
- 只有
)与(判读字符串是否为合法括号序列
原理是用栈来存,但是我们直接用一个 tot 来表示有多少左括号就好了
string s;
cin >> s;
int tot = 0, flag = 1;
for (auto it : s) {
if (it == '(') tot++;
else if (it == ')' ) tot--;
if (tot < 0) flag = 0;
}
if (flag) cout << "YES" << endl;
else cout << "NO" << endl;
解法一:
我们把括号抽象到二维平面坐标上,起点在 (0,0) ,遇到 ( 横坐标纵坐标都 +1,遇到)横坐标纵坐标都 -1。
对于)((())))(()()) 就变成了
每一个向下的线段就代表一个) ,每一个向上的线段就代表 (。可以发现,任意两个在同一水平线的点之间如果没有在这个水平线下的点,就表示一段合法的括号序列,例如B,H,I,O。我们就可以基于这个性质来做这个题。
我们从前向后把所有的下标压入栈中。如果遇到匹配的情况,我们就删除这一组,这样就便于下一组匹配。例如当DE--EF 匹配,DE 删除,EF不会压入栈中,之后CD 在 栈顶与 FG 就可以匹配。未匹配的括号就可以作为匹配串的分界点,方便我们更新答案例如AB 与HI。
#include <bits/stdc++.h>
using namespace std;
const int N = 1e6 + 10;
int st[N];
int main()
{
ios::sync_with_stdio(false);cin.tie(0); cout.tie(0);
string s;
cin >> s;
stack<int> sta;
int ans = 0;
int cnt = 0, ma =0;
for (int i = 0; i < s.length(); i++) {
if (!sta.empty() && s[i] == ')' && s[sta.top()] == '(') { sta.pop(); }
else sta.push(i);
int res = 0;
if (!sta.empty()) res = i - sta.top();
else res = i + 1;
if (res == ma) cnt++;
else if(res > ma) { ma = res; cnt = 1; }
}
if (ma)cout << ma << ' ' << cnt << endl;
else cout << "0 1" << endl;
return 0;
}
直接贪心,能匹配的都匹配,不能匹配就不管,用 tot 来计数模拟栈中元素。
#include <bits/stdc++.h>
using namespace std;
int main()
{
ios::sync_with_stdio(false);cin.tie(0); cout.tie(0);
string s;
cin >> s;
int tot = 0,ans = 0; ///有多少左括号
for (auto it : s) {
if (it == '(') tot++;
if (it == ')' && tot > 0) tot--,ans++;
}
cout << (ans << 1) << endl;
return 0;
}
10.2、奇数码
奇数码是八数码的一个扩展,在一个 \(n*n\) 的网格中进行,其中 \(n\) 为奇数, \(1\) 个空格和 \(1\) 到 \(n*n-1\) 个数恰好不重不漏地分布在 \(n*n\) 的网格中。空格移动的规则与八数码相同。
问是否能重一个局面,转移到另一个局面?
结论 : 奇数码游戏两个局面可达,当且仅当两个局面下网格中的数依次写成 \(1\) 行 $n*n -1 $ 个元素后(不考虑空格),逆序对个数的奇偶性相同。
推广: \(n\) 为偶数的情况,两个局面可达,当且仅当写成序列后,
逆序对数之差和两个局面下空格所在的行数之差奇偶性相同。
10.3、开关灯问题
\(n\times n\) 的 矩阵,按动可以使周围的灯都变换状态,初始全灭,如何全亮



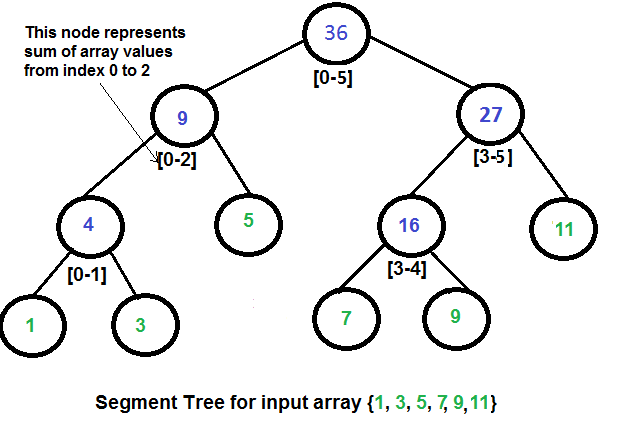

 浙公网安备 33010602011771号
浙公网安备 33010602011771号