【前言】树的遍历,根据访问自身和其子节点之间的顺序关系,分为前序,后序遍历。对于二叉树,每个节点至多有两个子节点(特别的称为左,右子节点),又有中序遍历。由于树自身具有的递归性,这些遍历函数使用递归函数很容易实现,代码也非常简洁。借助于数据结构中的栈,可以把树遍历的递归函数改写为非递归函数。
在这里我思考的问题是,很显然,循环可以改写为递归函数。递归函数是否借助栈这种数据结构改写为循环呢。因为函数调用中,call procedure stack 中存储了流程的 context,调用和返回相当于根据调用栈中的 context 进行跳转。而采用 stack 数据结构时,主要还是一个顺序循环结构,主要通过 continue 实现流程控制。
首先,给出遍历二叉树的序的定义:
(1)前序遍历:当前节点,左子节点,右子节点;
(2)中序遍历:左子节点,当前节点,右子节点;
(3)后序遍历:左子节点,右子节点,当前节点。
对二叉查找树 BST 来说,中序遍历的输出,是排序结果。所以这里我以一个 BST 的中序遍历为主要例子说明问题。一个简单的 BST 如下图所示(为了保证美观精确,下图由我临时编写的一个 VC 窗口程序绘制为样本进行加工得到的):
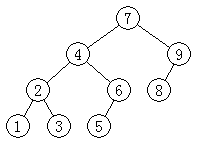
其中序遍历的输出为:1,2,3,4,5,6,7,8,9;
首先给出中序遍历的递归函数,代码如下:
1 typedef struct tagNODE 2 { 3 int nVal; 4 int bVisited; //是否被访问过 5 struct tagNODE *pLeft; 6 struct tagNODE *pRight; 7 } NODE, *LPNODE; 8 9 //中序遍历二叉树(递归版本) 10 void Travel_Recursive(LPNODE pNode) 11 { 12 if(pNode != NULL) 13 { 14 Travel_Recursive(pNode->pLeft); 15 _tprintf(_T("%ld, "), pNode->nVal); 16 Travel_Recursive(pNode->pRight); 17 } 18 }
很明显,对应于前面给出的定义,只需要调整上述代码中行号为 14,15,16 的顺序,就可以得到相应的遍历序。
现在,引入栈数据结构,它是一个元素为节点指针的数组,将上面的递归函数改写为非递归函数。中序遍历的基本方法是:
(1)将根节点 push 入栈;
(2)当栈不为空时,重复(3)到(5)的操作:
(3)偷窥栈顶部节点,如果节点的左子节点不为 NULL,且没有被访问,则将其左子节点 push 入栈,并跳到(3)。
(4)当被偷窥的节点没有左子树,pop 该节点出栈,并访问它(同时标记该节点为已访问状态)。
(5)当该节点的右子节点不为空,将其右子节点 push 入栈,并跳到(3)。
根据以上方法,给出非递归函数的中序遍历版本代码如下:
1 typedef struct tagNODE 2 { 3 int nVal; 4 int bVisited; //是否被访问过 5 struct tagNODE *pLeft; 6 struct tagNODE *pRight; 7 } NODE, *LPNODE; 8 9 //辅助数据结构 10 LPNODE g_Stack[256]; 11 int g_nTop; 12 13 //遍历二叉树,借助于stack数据结构的非递归版本 14 void TravelTree() 15 { 16 //while the stack is not empty 17 while(g_nTop >= 0) 18 { 19 //peek the top node in stack; 20 LPNODE pNode = g_Stack[g_nTop]; 21 22 //push left child; 23 if(pNode->pLeft != NULL && !pNode->pLeft->bVisited) 24 { 25 ++g_nTop; 26 g_Stack[g_nTop] = pNode->pLeft; 27 continue; 28 } 29 30 //pop and visit it; 31 _tprintf(_T("%ld, "), pNode->nVal); 32 pNode->bVisited = 1; 33 --g_nTop; 34 35 //push right child; 36 if(pNode->pRight != NULL && !pNode->pRight->bVisited) 37 { 38 ++g_nTop; 39 g_Stack[g_nTop] = pNode->pRight; 40 continue; 41 } 42 } 43 }
以前面的 BST 为例,在非递归函数中,栈状态的动态变化如下图所示(下图主要由 Excel 和 Photoshop 制作):

在上面的代码的 while 循环体内,可以分为三个小的代码块:
(1)pop 栈顶的节点,并访问此节点 (line 30 ~ 33);
(2)push 左子节点 (line 22 ~ 28);
(3)push 右子节点 (line 35 ~ 41);
只要调整 while 循环体中的这三个代码块的顺序,就可以分别实现三种遍历序。例如,前序:(1)(2)(3);后序:(2)(3)(1)。
从上面的代码中,有两点需要说明:
(1)最后一个代码块中的 continue 可以不需要写,但为了可以调整代码块的顺序,两个 continue 都是需要的。
(2)因为前序遍历的逻辑的简洁性,不借助于 bVisited 标记,也可以完成遍历,但为了通用,还是需要这个节点标记。
最后,补充上其他并不重要的方法,创建树,释放树,main 函数的代码如下(把已有所有代码拼在一起即构成完整的 Demo 程序):

//左右 Child 定义 #define LCHILD 0 #define RCHILD 1 typedef struct tagNODE { int nVal; int bVisited; //是否被访问过 struct tagNODE *pLeft; struct tagNODE *pRight; } NODE, *LPNODE; LPNODE g_Stack[256]; int g_nTop; LPNODE InsertNode(LPNODE pParent, int nWhichChild, int val) { LPNODE pNode = (LPNODE)malloc(sizeof(NODE)); memset(pNode, 0, sizeof(NODE)); pNode->nVal = val; if(pParent != NULL) { if(nWhichChild == LCHILD) pParent->pLeft = pNode; else pParent->pRight = pNode; } return pNode; } //递归释放二叉树的内存 void FreeTree(LPNODE pRoot) { if(pRoot != NULL) { FreeTree(pRoot->pLeft); FreeTree(pRoot->pRight); //_tprintf(_T("freeing Node (%ld) ...\n"), pRoot->nVal); free(pRoot); } } int _tmain(int argc, _TCHAR* argv[]) { //索引为 0 的元素不使用。 LPNODE pNodes[10] = { 0 }; pNodes[1] = InsertNode(pNodes[0], LCHILD, 7); pNodes[2] = InsertNode(pNodes[1], LCHILD, 4); pNodes[3] = InsertNode(pNodes[1], RCHILD, 9); pNodes[4] = InsertNode(pNodes[2], LCHILD, 2); pNodes[5] = InsertNode(pNodes[2], RCHILD, 6); pNodes[6] = InsertNode(pNodes[3], LCHILD, 8); pNodes[7] = InsertNode(pNodes[4], LCHILD, 1); pNodes[8] = InsertNode(pNodes[4], RCHILD, 3); pNodes[9] = InsertNode(pNodes[5], LCHILD, 5); //push 根节点 g_nTop = 0; g_Stack[g_nTop] = pNodes[1]; TravelTree(); _tprintf(_T("\n")); Travel_Recursive(pNodes[1]); _tprintf(_T("\n")); FreeTree(pNodes[1]); return 0; }
可以看到,释放树(FreeTree)这个函数,就是按照后序遍历的顺序进行释放的。
【补充】和本文相关的我写的其他博客文章:
(1)采用路径模型实现遍历二叉树的方法。2013-5-18;
(2)[非原创]树和图的遍历。2008-8-10;
【后记】
献给曾经向我请教“采用非递归方法遍历树”的 小玉(littlehead)学妹。




 浙公网安备 33010602011771号
浙公网安备 33010602011771号