对kmp算法的理解与应用

近日刷题是遇到了kmp算法,再进一步在b站上找网课学习之后,对此有了更深一步理解

对于长度为 mm 的字符串 ss，其前缀函数 \pi(i)(0 \leq i < m)π(i)(0≤i<m) 表示 ss 的子串 s[0:i]s[0:i] 的最长的相等的真前缀与真后缀的长度。特别地，如果不存在符合条件的前后缀，那么 \pi(i) = 0π(i)=0。其中真前缀与真后缀的定义为不等于自身的的前缀与后缀。

我们举个例子说明：字符串 aabaaabaabaaab 的前缀函数值依次为 0,1,0,1,2,2,30,1,0,1,2,2,3。

\pi(0) = 0π(0)=0，因为 aa 没有真前缀和真后缀，根据规定为 00（可以发现对于任意字符串 \pi(0)=0π(0)=0 必定成立）；

\pi(1) = 1π(1)=1，因为 aaaa 最长的一对相等的真前后缀为 aa，长度为 11；

\pi(2) = 0π(2)=0，因为 aabaab 没有对应真前缀和真后缀，根据规定为 00；

\pi(3) = 1π(3)=1，因为 aabaaaba 最长的一对相等的真前后缀为 aa，长度为 11；

\pi(4) = 2π(4)=2，因为 aabaaaabaa 最长的一对相等的真前后缀为 aaaa，长度为 22；

\pi(5) = 2π(5)=2，因为 aabaaaaabaaa 最长的一对相等的真前后缀为 aaaa，长度为 22；

\pi(6) = 3π(6)=3，因为 aabaaabaabaaab 最长的一对相等的真前后缀为 aabaab，长度为 33。

有了前缀函数，我们就可以快速地计算出模式串在主串中的每一次出现

 

 

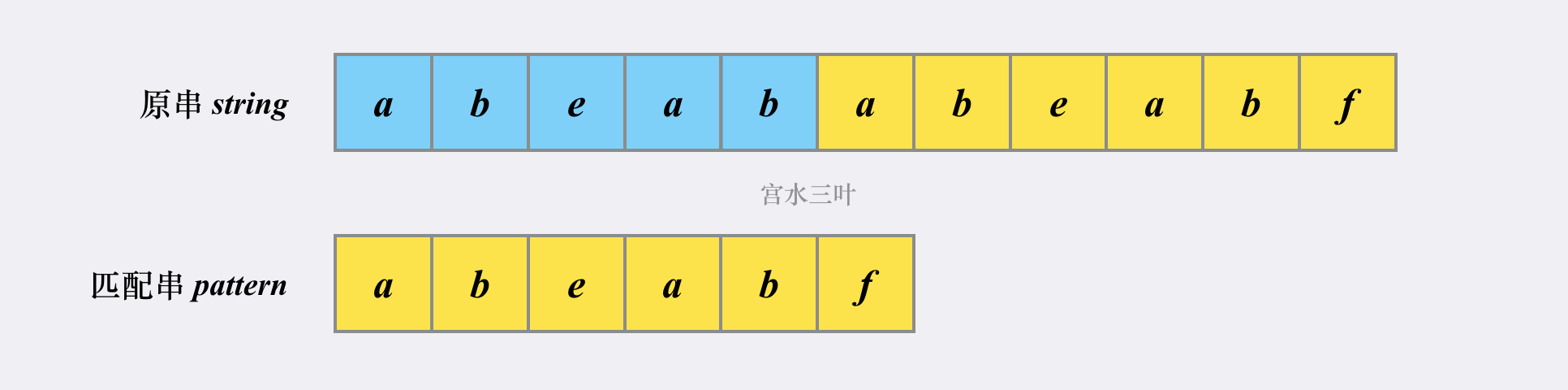
 这里借用力扣某位大佬的图解释下

我们可以先看看如果不使用 KMP，会如何进行匹配（不使用 substring 函数的情况下）。

首先在「原串」和「匹配串」分别各自有一个指针指向当前匹配的位置。

首次匹配的「发起点」是第一个字符 a。显然，后面的 abeab 都是匹配的，两个指针会同时往右移动（黑标）。

在都能匹配上 abeab 的部分，「朴素匹配」和「KMP」并无不同

作者：AC_OIer
链接：https://leetcode-cn.com/problems/implement-strstr/solution/shua-chuan-lc-shuang-bai-po-su-jie-fa-km-tb86/
来源：力扣（LeetCode）

而kmp算法之所以能够简化运算的原因,就在于其next数组,next数组帮助你跳过了很多不正确的选项,使运算更加简单,下面我们用一行简单的代码来求解next数组

void getvoid GetNext(int next[],int length,char *s){

void GetNext(char*s,int length,int next[])

{

    next[0]=0;

    int i=1,j=0;

//首先我们初始化j等于零,其中,j表示的是模式串前缀的最后一个数的下标志,同时也表示前后缀相同的最大值,j表好似的是后缀的最后一个下标所指的位置

    for(i=1;i<length;i++){

        while(j>0 && s[i]!=s[j]){

            j=next[j-1];　　　　　　//当其不相等的时候,用while循环回溯

        }

        if(s[i]==s[j])　　　　　　　//相等的时候j向前加

        {

            j++;

        }

        next[i]=j;　　　　　　　　//更新next数组,,主义,这里使用next[i]=j

    }

}

    

int strStr(char* haystack, char* needle) {

    int numssize1=strlen(haystack);

    int numssize2=strlen(needle);//先得到模式串和目标川的长度

    

    if(numssize2==0){

        return 0;//若模式串的长度为零,返回零,符合c语言中的定义???

    }

    int next[numssize2];

    int j=0,i=0;

    GetNext(needle,numssize2, next);//初始化next数组

    for(i=0;i<numssize1;i++)

    {

        while(j>0 && haystack[i]!=needle[j]){   //此时的i和j和上文的i,j表示的意思不同,初学者常犯的错误(当然也包括我)

            j=next[j-1];                                  //若匹配不成功 则回溯,正是在这一步简化了运算,为何,因为既然数组下标能够加到j,说明其前面的几个数必然已经和目标串的前j个字符

                                                              //匹配成功了,那么这时i不动,我们只需要在比较第needle[next[j-1]+1]和haystack[i]即可,换句话说,

                                                              //此时重置了匹配进程,haystack中只有前next[j-1]个数被用到了,而不是向之前一样j个都被用到了,

                                                             //相反,此时若匹配失败的话,将会因为while循环不断回溯,一直到0时,将会(注意此时,j任然指向needle)

        }

        if(haystack[i]==needle[j]){

            j++;                                         //此时如匹配成功,j++

        }

        if(j==numssize2)                      //说明历经考研之后,j成功来到了了末尾,注意!此时j在最后一次时为j-1,相等后+1,即此时next[j]已经越界了,知识我们没有使用而已,此后如要

        return (i-numssize2+1);              //重新使用的话,还是得小心

                                                          //此时i已经指到对应位置+numssize的地方,又根据题意要求,我们加上1

    }

    return -1;                                   //若经历了所有遍历后,函数没有在上一个出口返回,说明没有目标川中没有与模式串匹配的地方,那么,返回-1

}

想说的,该注意的点都已经,写在注释里,希望能对大家有所帮助!!!