图总结

一、思维导图

 

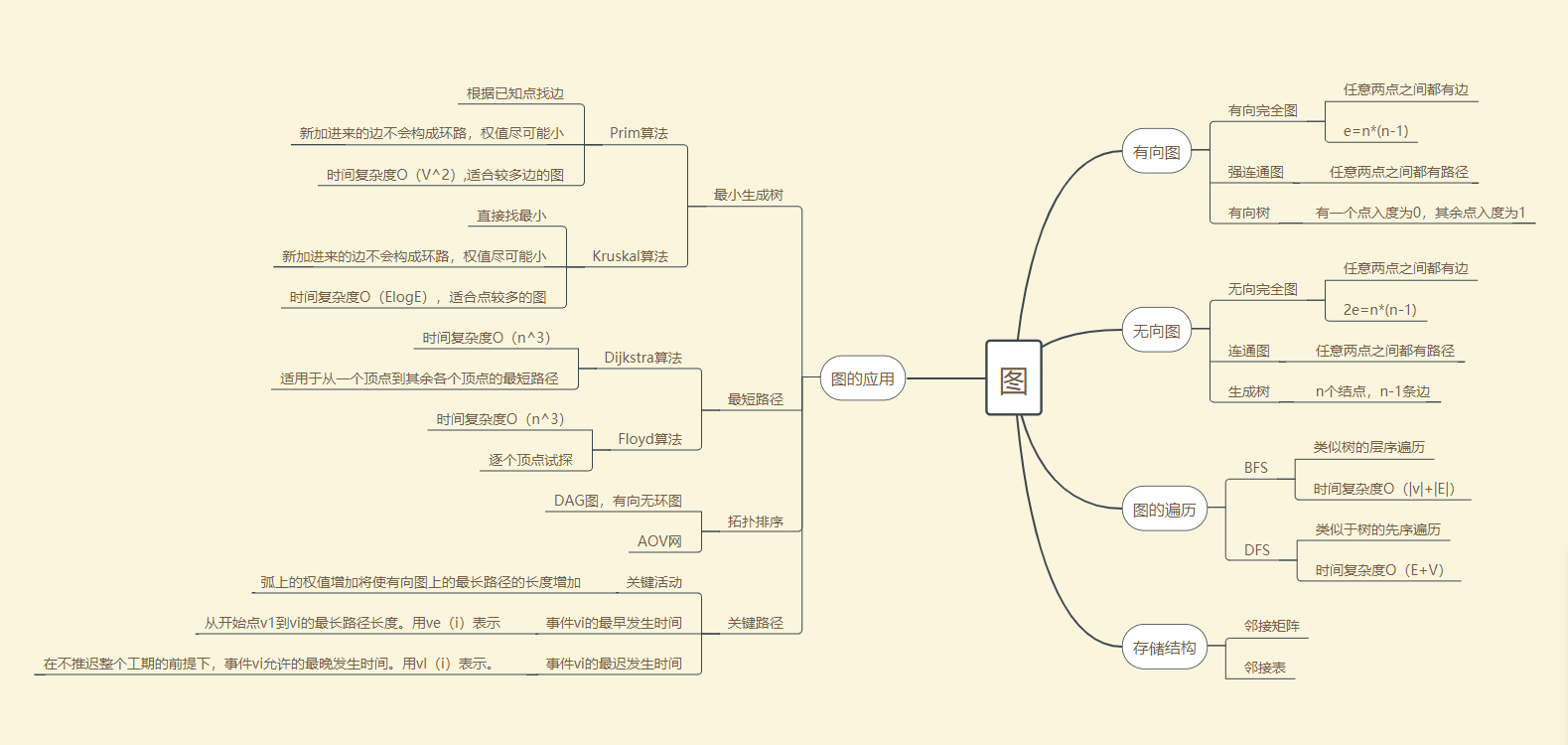
 二、重要概念的笔记

1.图的遍历

深度优先遍历(DFS)：深度优先遍历的思想类似于树的先序遍历。其遍历过程可以描述为：从图中某个顶点v出发，访问该顶点，然后依次从v的未被访问的邻接点出发继续深度优先遍历图中的其余顶点，直至图中所有与v有路径相通的顶点都被访问完为止。

 

 

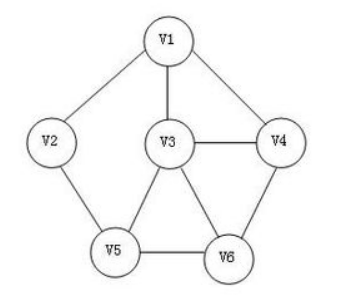
遍历序列为V1→V2→V5→V3→V4→V6

广度优先遍历（BFS）：图的广度优先遍历算法是一个分层遍历的过程，和树的层序遍历算法类同，是从图的某一顶点V0出发，访问此顶点后，依次访问V0的各个未曾访问过的邻接点；然后分别从这些邻接点出发，直至图中所有已被访问的顶点的邻接点都被访问到；若此时图中尚有顶点未被访问，则另选图中一个未被访问的顶点作起点，重复上述过程，直至图中所有顶点都被访问为止。

 

 

 

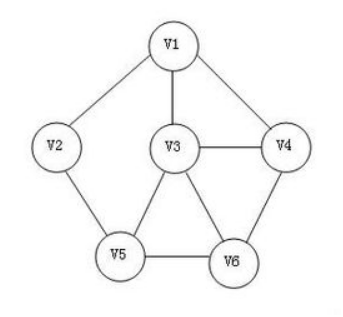
遍历序列为V1→V2→V3→V4→V5→V6

 

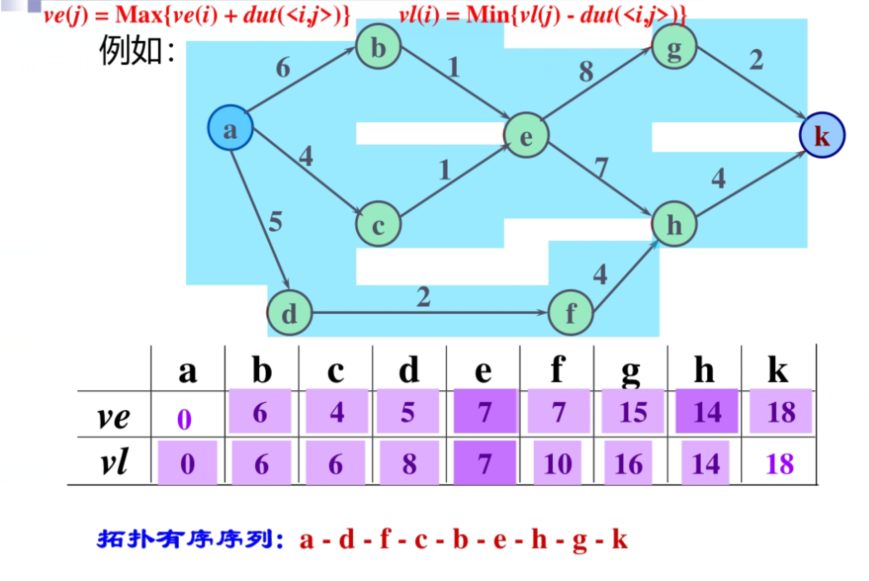
2.拓扑排序

 

 

DAG有向无环图

 

AOV网：顶点表示活动，弧表示活动间先后关系的有向图，即活动在顶点上的网络

 

拓扑序列：将AOV所有顶点v0,v1,...vn-1排成线性序列vi0,vi1,...vin-1，满足：若vi到vj有一条路径，则vi排在vj前面。vi0,vi1,...vin-1就是一个拓扑序列（不一定唯一）

 

拓扑排序步骤：

 

在有向图中选一个入度为0的顶点，且输出；

 

在图中删除该顶点和以它为尾的弧；

 

重复这两部，直至全部顶点输出，此时得到无环有向图的所有顶点的拓扑序列；或者图中剩下顶点中再也没有入度为0的顶点，此时拓扑序列不存在，且图中必有环。

 

 

3.最小生成树

构造的最小生成树并不一定唯一，但最小生成树的权值之和一定是相同的。

Prim算法

void Prim(MGraph g,int v){
    int lowcost[MAXv];
    int min;
    int closest[MAXV],i,j,k;
    for(i=0;i<g.n;i++){
        lowcost[j]=g.edges[v][i];
        closest[i]=v;
    }
    for(i=1;i<g.n;i++){
        min=INF;
        for(j=0;j<g.n;j++){
            if(lowcost[j]!=0&&lowcost[j]<min){
                min=lowcost[j];
                k=j;
            }
            printf("边(%d,%d)权为：%d\n",closest[k],k,min);
            lowcost[k]=0;
        }
        for(j=0;j<g.n;j++){
        if(g.edges[k][j]!=0&&g.edges[k][j]<lowcost[j]){
                lowcost[j]=g.edges[k][j];
                closest[j]=k;
            }
        }
    }
}

 

Kruskal算法

void Kruskal(MGraph g){
    int i,j,u1,v1,sn1,sn2,k;
    int vset[MAXV];
    Edge E[MaxSize];
    k=0;
    for(i=0;i<g.n;i++){
        for(j=0;j<g.n;j++){
            if(g.edges[i][j]!=0&&g.edges[i][j]!=INF){
                E[k].u=i;E[k].v=j;
                E[k].w=g.edges[i][j];
                k++;
            }
        }
    }
    InsertSort(E,g,e);
    for(i=0;i<g.n;i++) vest[i]=i;
    k=1;j=0;
    while(k<g.n){
        u1=E[j].u;v1=E[j].v;
        sn1=vset[u1];sn2=vset[v1];
        if(sn1!=sn2){
            cout<<u1,v1,E[j].w;
            k++;
            for(i=0;i<g.n;i++)
                if(vset[i]==sn2) 
                    vset[i]=sn1;
        }
        j++;
    }
}

4.最短路径

Dijkstra算法

 

 

 

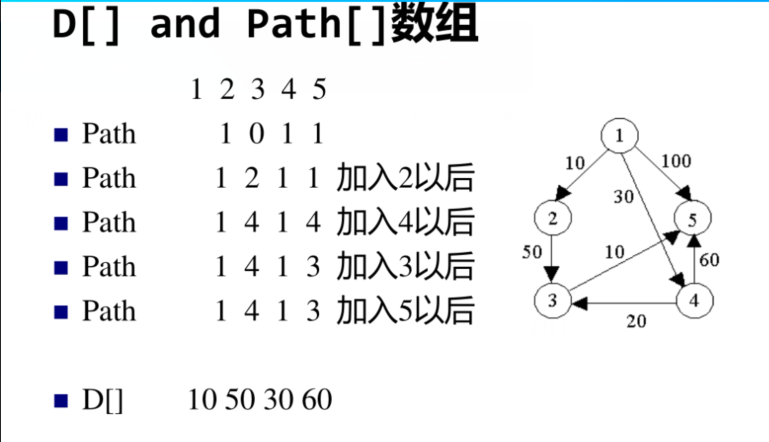
算法实现：

 

 

三、疑难问题

 

 

#include<iostream>

using namespace std;

#define MAXVEXNUM 501
//点,边
typedef  int ArcCell;
typedef char VexType;

typedef struct {
    VexType vexs[MAXVEXNUM];//点的集合
    ArcCell arcs[MAXVEXNUM][MAXVEXNUM];//边的集合
    int vexNum, arcNum;
    int color[MAXVEXNUM];
}MyGraph;

void CreateDGraphFromConsole(MyGraph& G, int vexNum, int arcNum);
int JudgeGraph(MyGraph& G);

int main() {
    int n, i, e, k, j, m,t,x;
    int min,max;
    int V[MAXVEXNUM];
    MyGraph G;
    cin >> n >> e>>k;
    CreateDGraphFromConsole(G, n, e);
    cin >> m;
    for (i = 0; i < m; i++) {
        min = 500;
        max = 0;
        t = 0;
        for (j = 0; j < n; j++) {
            cin >> G.color[j];
            for (x = 0; x < t; x++) {
                if (V[x] == G.color[j])
                    break;
            }
            if (x == t) {
                V[t++] = G.color[j];
            }
        }
        if (t != k) {
            cout << "No" << endl;
        }
        else {
            if (JudgeGraph(G))
                cout << "Yes" << endl;
            else
                cout << "No" << endl;
        }
    }
}
void CreateDGraphFromConsole(MyGraph& G, int vexNum, int arcNum) {
    int i, j, k;
    int a,b;
    G.vexNum = vexNum;
    G.arcNum = arcNum;
    for (i = 0; i < vexNum; i++) {
        for (j = 0; j < vexNum; j++)
            G.arcs[i][j] = 0;
    }
    for (k = 0; k < arcNum; k++) {
        cin >> a >> b;
        G.arcs[a-1][b-1] = 1;
        G.arcs[b-1][a-1] = 1;
    }
}
int JudgeGraph(MyGraph& G) {
    int i, j;
    for (i = 0; i < G.vexNum; i++) {
        for (j = 0; j < G.vexNum; j++) {
            if (G.arcs[i][j]) {
                if (G.color[i] == G.color[j])
                    return 0;
            }
        }
    }
    return 1;
}