BUAA_OO第三单元总结性博客作业——JML
在第三单元的面向对象课程中我们第一次接触了JML语言以及基于JML规范的规格化设计。在之前一系列关于面向对象思想的学习认识中,我们知道了Java是一种面向对象的语言,面向对象思想的一个重要原则就是将过程性的思考尽可能地延迟。而作为Java建模语言,JML给予了我们一种全新的方式来看待Java的类和方法,其通过将一些符号语言显式地插入到Java程序代码中,来描述一个方法所要求的前提以及期望达到的效果,而将过程性的思考延迟到了方法的设计中。
JML理论基础
JML是用于对Java程序进行规格化设计的一种表示语言,是一种行为接口规格语言,基于Larch方法构建,BISL提供了对方法和类型的规格定义手段。
使用JML来声明性的描述一个方法或类的预期行为可以显著提高整体的开发进程,JML引入了大量用于描述方法行为的结构,例如:模型域、量词、断言可视范围、预处理、后出路、条件继承、正常行为规范(normal_behavior)以及异常行为规范(exceptional_behavior)等。
其中,对数据规格的抽象主要有两种:
约束(constraint):主要描述数据状态变化应该满足的要求
不变式(incariant):主要描述数据状态应该满足的要求
对方法行为的规格描述包括:
前置条件(requires):描述方法输入数据的要求
后置条件(ensures):方法执行结果满足的约束
作用范围(assignable):方法能够修改的类成员属性
以及相应的JML表达式:
原子表达式
\result表达式:表示一个非 void 类型的方法执行所获得的结果,即方法执行后的返回值。
\old( expr )表达式:用来表示一个表达式 expr 在相应方法执行前的取值。
\not_assigned(x,y,...)表达式:用来表示括号中的变量是否在方法执行过程中被赋值。
\not_modified(x,y,...)表达式:与上面的\not_assigned表达式类似,该表达式限制括号中的变量在方法执行期间的取 值未发生变化。
\nonnullelements( container )表达式:表示 container 对象中存储的对象不会有 null 。
\type(type)表达式:返回类型type对应的类型(Class)。
\typeof(expr)表达式:该表达式返回expr对应的准确类型。
量化表达式
\forall表达式:全称量词修饰的表达式。
\exists表达式:存在量词修饰的表达式。
\sum表达式:返回给定范围内的表达式的和。
\product表达式:返回给定范围内的表达式的连乘结果。
\max表达式:返回给定范围内的表达式的最大值。
\min表达式:返回给定范围内的表达式的最小值。
\num_of表达式:返回指定变量中满足相应条件的取值个数。
将这些建模标记,包括表达式语句等的规格描述,以JAVA注释的方式加入到程序代码中,对正常编译没有影响,并且能够精确地描述代码、减少bug的出现以及规范用户对类与方法的使用。JML可用于开展规格化设计,在代码工作开始前规范代码行为,也可针对已有的代码实现书写其相应规格,从而提高可维护性。
JML应用工具链情况
可以使用开源的JML编译器来编译含有JML标记的代码,所生成的类文件会在运行时自动检查JML规范,若程序未实现规范中规定的事情,JML运行期断言检查编译器会抛出一个unchecked exception来说明程序违背了哪一条规范。JMLdoc工具与Javadoc工具类似,可在生成的HTML格式文档中包含JML规范,JMLUnit可以生成一个Java类文件测试的框架。SMT Solver工具可以以静态方式来检查代码实现对规格的满足情况。
二、SMT Solver
SMT:(可满足性模理论-Satisfiability Modulo Theories)
在计算机科学和数学逻辑中,可满足性模理论(SMT)问题是关于经典一阶逻辑中表达的背景理论与等式相结合的逻辑公式的决策问题。通常在计算机科学中使用的理论的例子是实数理论,整数理论以及诸如列表,阵列,位向量等各种数据结构的理论。SMT可以被认为是一种形式约束满足问题,从而形成约束规划的某种形式化方法。——摘自知乎
openjml使用SMT Solver来对检查程序实现是否满足所设计的规格(specification)。目前openjml封装了四个主流的solver,包括z3,cvc4,simplify与yices2。
三、JMLUnitNG/JMLUnit
我自行构造了一份java代码,并为其撰写了JML规格,使用jmlunitng来生成测试数据。
代码如下:
1 package demo; 2 3 public class Demo { 4 /*@ public normal_behaviour 5 @ ensures \result == lhs + rhs; 6 */ 7 public static long compare(long lhs, long rhs) { 8 return lhs + rhs; 9 } 10 11 /*@ public normal_behavior 12 requires param >= 0; 13 ensures \result >= 10; 14 also public normal_behavior 15 requires param < 0; 16 ensures \result < -10; 17 @*/ 18 public static int makeHole(int param) { 19 if(param >= 0) { 20 return param + 10; 21 }else{ 22 return param - 10; 23 } 24 } 25 public static void main(String[] args) { 26 compare(114514,1919810); 27 makeHole(10); 28 makeHole(-10); 29 } 30 }
使用jmlunitng生成测试文件
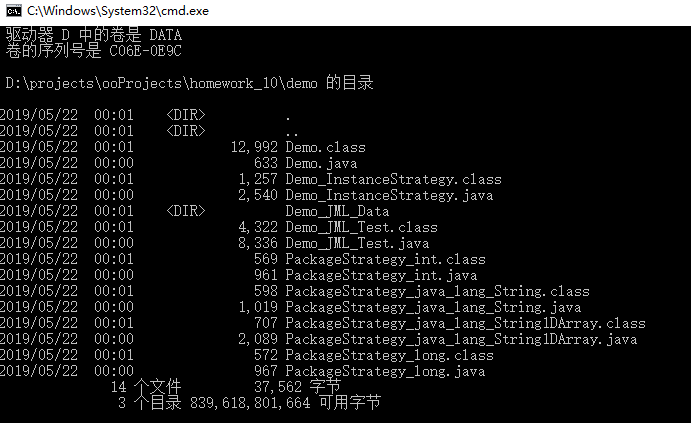
生成文件树:

使用javac编译测试文件
执行测试
过程示意图如下:
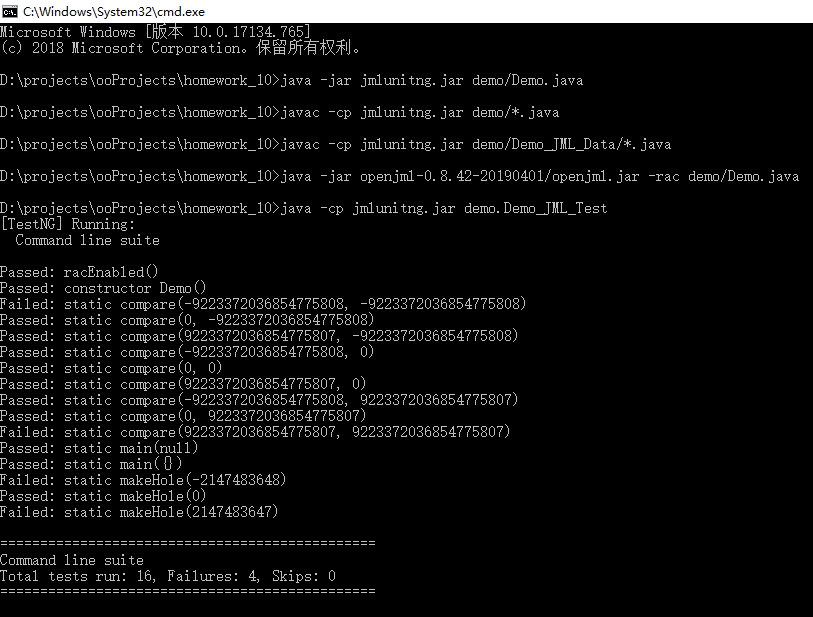
从jmlunitng反馈的结果来看,上述代码对JML规格的实现还是存在问题的。从自动生成的测试样例给出的数据分析,原代码的实现对于compare与makeHole方法均存在整数溢出的问题。
四、架构设计
第一次作业
这次作业主要是实现Mypath与MypathContainer两个分别继承Path与PathContainer两个官方提供接口的类。
Path类中主要存储一个路径内的所有结点,按照规格说明,我使用HashMap存储每一个结点序号与结点之间的对应关系,并自行构建了一个HashSet数组,存储所有的DistinctNode,getDistinctNodeCount()方法直接返回HashSet数组的大小,并设计一个getDistinctNode()方法,使得PathContainer类能够获取Path类中的HashSet数组,在计算PathContainer中的所有不同结点数时,能够简化对每一个Path中相同结点的计数。
PathContainer类主要存储各个path,并为每个path分配Pathid,我使用两个hashmap来建立path与pathid之间的双向映射,使得通过path得到id或者通过pathid查找path都是O(1)的复杂度,以空间换时间,这个方法需要重写path类的hashcode。同样地,在PathContainer中也使用了一个名为dinstictNodeList的HashMap来存储不同结点,key为每一个Node的值,value为Node的出现次数,在每一次add与remove时通过path的getDistinctNode()方法维护这个hashmap,将对dintinctNode的处理分散到每一个add与remove中,减小了时间复杂度。
第一次作业架构:
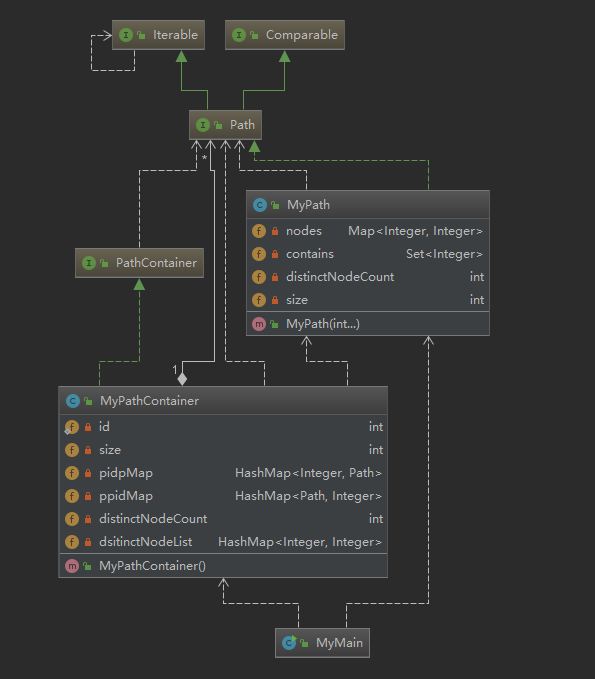
第二次作业
第二次作业相对第一次作业,将PathContainer类拓展成了Graph类,实际上就是将第一次作业PathContainer中两两之间相对独立的Path连通,实现一个由诸多结点,路径组成的无向图系统。
第二次作业相对第一次作业,仅仅多实现了containsNode(),containsEdge(),isConnected(),getShortestPathLength(),四个方法。我基本没有改动第一次作业的任何代码,对于第一个containsNode()方法,直接返回dintinctNodeList中是否含有这个node即可。对于后三个方法的实现,则需要在MyGraph类中,增加对图的处理,由于第二次作业对图的的处理较为简单(也为了偷懒),我并没有将图单独封装成一个类,而是在MyGraph中新增了一个静态二维数组egraph以及一个存储边的名为edges的HashMap来实现。
对于图的处理,主要通过addtograph(),removefromgraph(),updateNodes()这三个方法维护图的结构(同时更新了Graph中所含的edges),通过floyd()方法进行最短路径计算(同时也计算出了两个结点是否连接)。主要实现如下:
当收到add与remove指令时,首先更新edges数组:
若为add指令,直接向edges中塞入path中所含的所有边;
若为remove指令则较为繁琐,需要判断这个结点在图中出现了几次,再确定是否要从distinctNodeList以及edges中移除。
接着调用floyd()方法,使用floyd算法计算图中所有结点之间的最短路径。在这里使用了egraph静态数组作为存储边的邻接矩阵。需要说明的是,为了构造每一个node与静态数组下标index的一一映射,我使用两个hashmap构造了node与数组下标的双向映射。并在每一次floyd进行前,都重新构建node与index的映射关系,并根据映射以及edges中存储的边重置邻接矩阵。这样实现虽然繁琐,但确保了每次使用floyd算法对这个n*n的静态数组进行计算时,n的大小都等于此时Graph中distinctNodeCount的大小,一定程度上减小了时间复杂度。
floyd算法具体实现:
1 protected void floyd() { 2 //清空映射关系 3 indexnodemap.clear(); 4 nodeindexmap.clear(); 5 //清空邻接矩阵 6 if (edges.isEmpty()) { 7 for (int i = 1; i <= distinctNodeCount; i++) { 8 for (int j = 1; j < distinctNodeCount; j++) { 9 if (i == j) { 10 egraph[i][j] = 0; 11 } else { 12 egraph[i][j] = INF; 13 } 14 } 15 } 16 return; 17 } 18 int index = 1; 19 //建立映射关系 20 for (int node : dsitinctNodeList.keySet()) { 21 indexnodemap.put(index, node); 22 nodeindexmap.put(node, index); 23 index++; 24 } 25 //重置邻接矩阵 26 for (int i = 1; i <= distinctNodeCount; i++) { 27 for (int j = 1; j <= distinctNodeCount; j++) { 28 if (i == j) { 29 egraph[i][j] = 0; 30 } else { 31 String key = 32 gethash(indexnodemap.get(i), indexnodemap.get(j)); 33 if (edges.containsKey(key)) { 34 egraph[i][j] = 1; 35 } else { 36 egraph[i][j] = INF; 37 } 38 } 39 } 40 } 41 //核心算法 42 for (int k = 1; k <= distinctNodeCount; k++) { 43 for (int i = 1; i <= distinctNodeCount; i++) { 44 for (int j = 1; j <= distinctNodeCount; j++) { 45 if (egraph[i][j] > egraph[i][k] + egraph[k][j]) { 46 egraph[i][j] = egraph[i][k] + egraph[k][j]; 47 } 48 } 49 } 50 } 51 }
第二次作业架构:
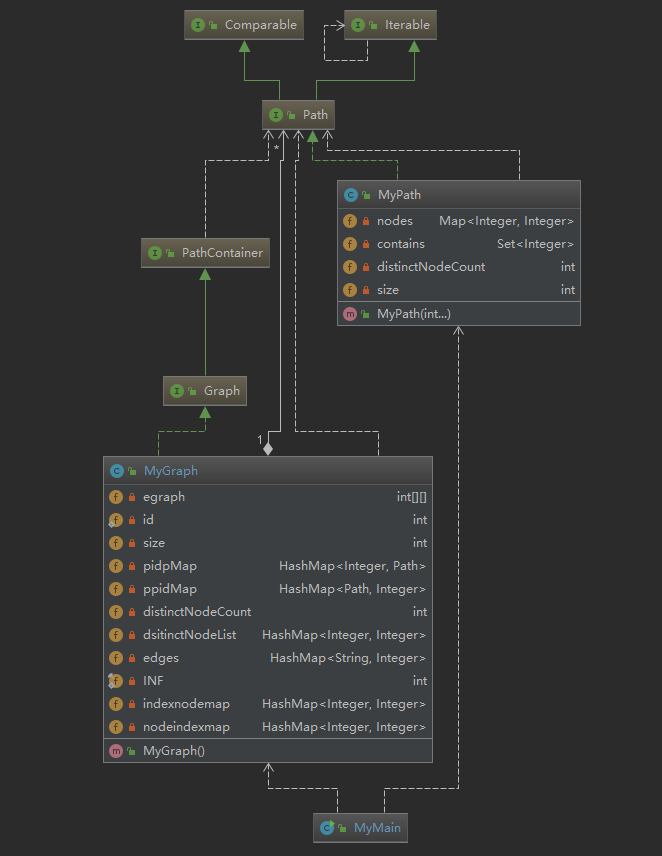
第三次作业
第三次作业我同样采用了第二次作业的总体思路,但由于这次作业中对图的处理较为繁琐,迫不得已我封装了一个MyRailWayGraph类,将与图有关的计算全放在这个图类中进行。
相比第二次作业,第三次作业也仅仅增加了4个方法,但这四个方法中每一个方法都需要为其设计专门的存储结构。
我最先解决的是最小联通块的问题,采用了并查集的思想。使用了一个名为prev的HashMap来存储各个结点之间的连通性。在每一次add之后调用union()方法,遍历prev并更新连通结点,在每一次remove之后就比较麻烦了,需要清空prev数组,并且遍历图中所有的Path,重新得到prev数组,具体实现在unionAfterRemove()方法中。最后得到的连通块个数就是prev数组中value的种类。
对于剩下的三个涉及到权值的“最小问题”,我采用了讨论区中大佬的算法,将剩下的三个方法统一建模,与第二次作业中的最短路径问题所用的邻接矩阵放在一起,在同一次floyd算法下跑一遍,得到任意两个不同结点之间的各种最小值。
具体实现包括:
对于LeastTransfer(最小换乘次数),构建换乘图,首先把一个Path中所有节点之间的权重全部设置为1。这样的话,我们从节点i1到节点i2的搭乘线路数就是以1为权值的图的最短路径,最小换乘数=最短线路数-1。
对于LeastPrice(最小票价),构建票价图,首先把一个Path中所有边的weight设置为1,对每一个Path单独用floyd算法跑一遍,Path内部的两个结点均为连通的,算出path内部两个结点之间的票价(这样算出的结果也可以理解在同一个路径中两个节点之间的票价,不需要换乘)。在每次构建邻接矩阵时,为体现换乘数,再将所有设置的边权值加2存在邻接矩阵中,若两个节点同时存在于不同路径中,则取最小值存入。最后的最低票价即为floyd以该权重计算出的最短路径 - 2。
对于LeastUnpleasantValue(最小不满意度),构建满意度图,同样需要首先把一个Path中所有点连通,先计算出路径中每条边的不满意度,再使用floyd算出路径内所有节点之间的不满意度。在每次构建邻接矩阵时,为体现换乘,将所有权重加32存入满意度图中。最低不满意度 = floyd以该权重计算出的最短路径 - 32。
floyd算法具体实现:
1 for (int k = 1; k <= nodenum; k++) { 2 for (int i = 1; i <= nodenum; i++) { 3 for (int j = 1; j <= nodenum; j++) { 4 //最短路径 5 if (egraph[i][j] > egraph[i][k] + egraph[k][j]) { 6 egraph[i][j] = egraph[i][k] + egraph[k][j]; 7 } 8 //最小换乘 9 if (leastTransferGraph[i][j] > leastTransferGraph[i][k] + leastTransferGraph[k][j]) { 10 leastTransferGraph[i][j] = leastTransferGraph[i][k] + leastTransferGraph[k][j]; 11 } 12 //最小票价 13 if (leastPriceGraph[i][j] > leastPriceGraph[i][k] + leastPriceGraph[k][j]) { 14 leastPriceGraph[i][j] = leastPriceGraph[i][k] + leastPriceGraph[k][j]; 15 } 16 //最小不满意度 17 if (leastUnpleasantValueGraph[i][j] > 18 leastUnpleasantValueGraph[i][k] + leastUnpleasantValueGraph[k][j]) { 19 leastUnpleasantValueGraph[i][j] = 20 leastUnpleasantValueGraph[i][k] + leastUnpleasantValueGraph[k][j]; 21 } 22 } 23 } 24 }
在每次add与remove之后,都会进行一遍上述计算过程,接下来任意调用与那四个“最短问题”有关的方法就只需要根据映射直接从矩阵从取出数据。由于add与remove指令最多只有50条,且限制了distinctNode最多为120个,floyd算法在边多节点少的情况下占有优势,实测并不会出现CPU时间过长的情况。
第三次作业架构
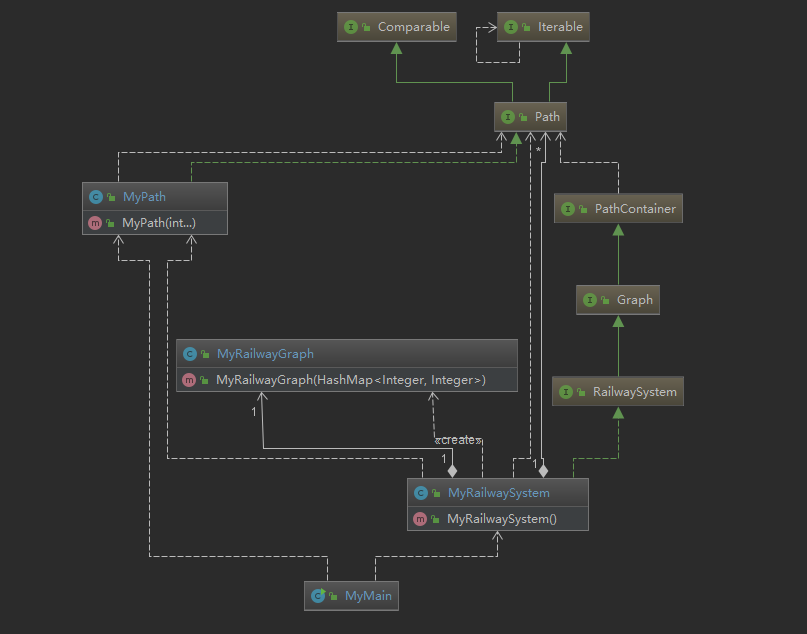
三次作业间的继承与拓展
第三单元三次与JML规格有关的作业体现出了继承式增量设计,人为构造需求的增量和可能的一些变化,从课程组提供的接口文件可以看出,每一次作业需要实现的接口都继承了上一次作业,并在上一次作业的基础上新增了几个方法。Mypath类在第一次作业写好之后三次作业基本就没有动过它,MyPathContainer类一直继承发展到了MyRailwaySystem类。论方法所占比重来看,第一次作业实现的方法是最多的,但每一个方法也相对简单。而后两次作业每次都只需要增加少数的几个方法,但每个方法都需要设计复杂的数据结构与算法为其服务。这三次作业最理想的设计应该是每一次作业都保留上一次的类,并分别新建MyGraph类与MyRailwaySystem类,分别继承上一个类,形成"MyPathContainer---MyGraph---MyRailwaySystem"这样的继承关系,但由于我在写代码时未处理好将变量修饰为protected时checkstyle的报错问题,后两次作业我都是直接在前一次类的基础上直接改名字并直接敲代码来实现的……
五、bug分析
三次作业在公测与互测中均没有被发现bug,由于指导书上的话,
公测和互测都将使用指令的形式模拟容器的各种状态,从而测试各个接口的实现正确性,即是否满足JML规格的定义。可以认为,只要代码实现严格满足JML,就能保证正确性。
对于每一个方法,我都看了一遍接口源代码给出的规格说明,避开了一些坑。
但是在代码书写完毕本地运行测试时,还是发现了一些bug。
第二次作业测试中发现了数组越界的bug,第二次作业总节点个数不超过250个,而我只开了大小为int[250][250]的二维数组,在跑共有250个不同节点的极限数据时发生数组越界,最后通过扩大数组解决。
第三次作业测试中,对于四个“最短问题”,忽略了当两个节点相等时的处理,导致出错。
由于第三次作业输入格式较为简单,我自己用C捏了一个简单的数据生成器,使用rand()函数造了许多随机数据,对自己的代码进行了大量功能测试与压力测试,确保了正确性。
六、心得体会
架构设计不是一个阶段,而是一个活动,是一种思维方式
在前面的作业中老师与助教多次强调要要合理设计自己代码的架构,减少重构,但迫于完成作业的压力,我并没有在特别注意架构问题。直到这两次作业我才逐渐认识到了架构的重要性。特别是这一单元的作业,课程组为我们提供了现成的接口设计,直接推动我们按照课程组希望的方向设计我们的架构,让我们把重心放在了各个方法的设计以及规格的实现上。当然,架构与方法实现是相辅相成的,好的架构能让方法的具体实现更加游刃有余,避免了复杂凌乱的代码带来的灾难。
在这一单元我们第一次接触到了规格以及基于规格的代码实现。在老师上课对规格的描述中,多次提到了规格之于代码设计与代码验证的重要性。在第一次实验课接触到规格以及自己书写几段简单的规格后,对规格这种繁琐的表述方式还是有点不理解,为了设计的严谨,撰写规格的时间会远远超过直接敲代码的时间,不可否认有完备的规格之后,代码的实现将会变得容易,但为此付出的代价是否背离了一开始写代码的初衷。老师上课也提到过,对一般的企业用户来说,程序员更愿意通过大量测试来验证代码的正确性,只有对正确性要求非常高的工业界,愿意花大量成本构造完备的规格验证。相信OO课程组如此大力地介绍规格的重要,是为了培养我们的工程化意识,锻炼我们的工程能力。



 浙公网安备 33010602011771号
浙公网安备 33010602011771号