【学习笔记】从零开始的导数
这段时间学习了一下数学上的导数和导函数，决定写一篇从零开始的学习笔记，保证一个没有学过任何导数知识的初中生只要愿意看都能看懂。
本文主要为了使读者更好地理解，对于概念性的东西可能不甚严谨，抱歉！
如果有关于概念的建议，也欢迎留言建议。
1. 平均变化率
1.1 定义
定义 : 对于一个函数 \(f(x)\), 其在 \([x_1, x_2]\) 的区间内的平均变化值定义为 过 \((x_1, f(x_1)), (x_2, f(x_2))\) 的直线的斜率。（\(x_1≠x_2\)）
所以易得到 ：(设平均变化率为 \(k\)) \(k = \frac{f(x_1)-f(x_2)}{x_1-x_2}\)
也可以写成 : \(k = \frac{\Delta y}{\Delta x}\) ( \(\Delta y = y_1-y_2=f(x_1)-f(x_2) ; \Delta x= x_1-x_2\))
1.2 图像 & 性质
对于过 \((x_1, f(x_1)), (x_2, f(x_2))\) 的直线，易理解这是函数的一条割线。
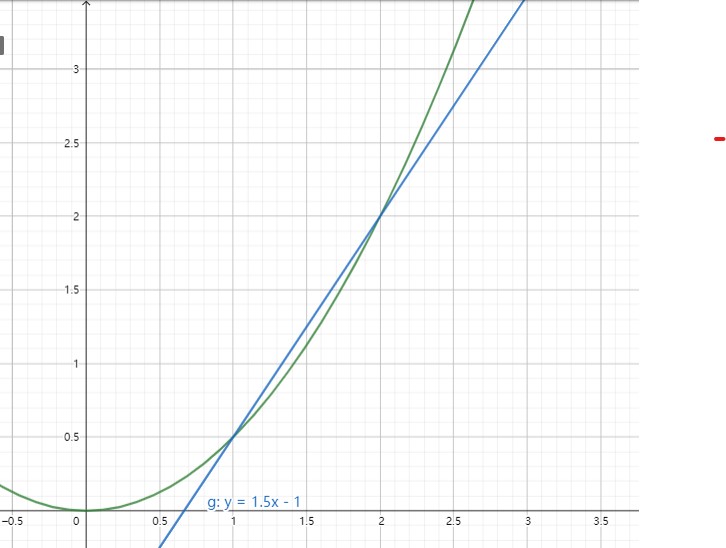
上图 : 对于函数 \(f(x)=\frac{1}{2}x^2\), 对于这个函数在 \([1, 2]\) 的区间内的平均变化值(过 \((1, \frac{1}{2}), (2, 2)\)) 对应的直线
这个性质看上去没什么用，不过下面的小节我们会了解到这条性质特殊化后的意义（剧透：函数的割线 \(\rightarrow\) 函数的切线）
1.3 应用
除了出题，貌似没有任何应用。
For OIers & ACMers: 洛谷习题 【数学 1.1.1】平均变化率
2. 切线 & 导数
2.1 定义
切线定义 : 对于一个函数 \(f(x)\), 过 \((x_1, f(x_1))\) 且仅过该点的一条直线称为过该点的切线。
导数定义 : 对于一个函数 \(f(x)\), 过 \((x_1, f(x_1))\) 且仅过该点的一条直线的斜率称为过该点的导数。（这跟后面要说的导数有很大不同。事实上，我们一般说的导数（也就是后面要说的）是导函数的简称）
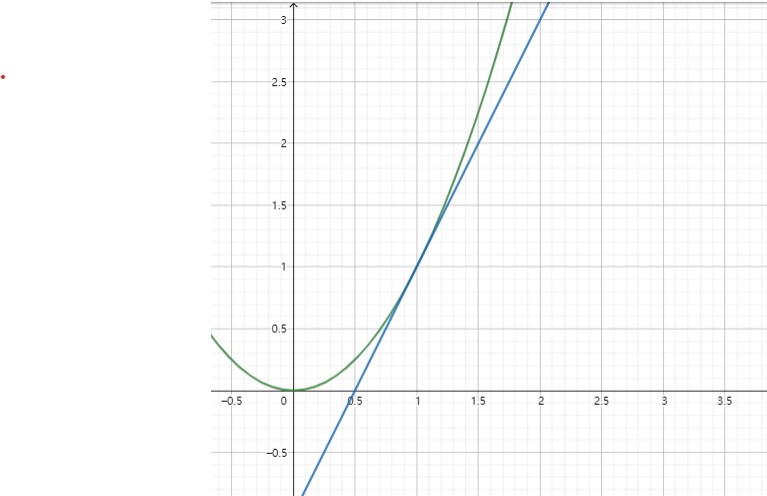
如图，为 \(f(x)=x^2\) 于 \((1, 1)\) 处的切线 \(y=2x-1\) (导数为 \(2\))。
但要注意，上述的定义是不严谨的！
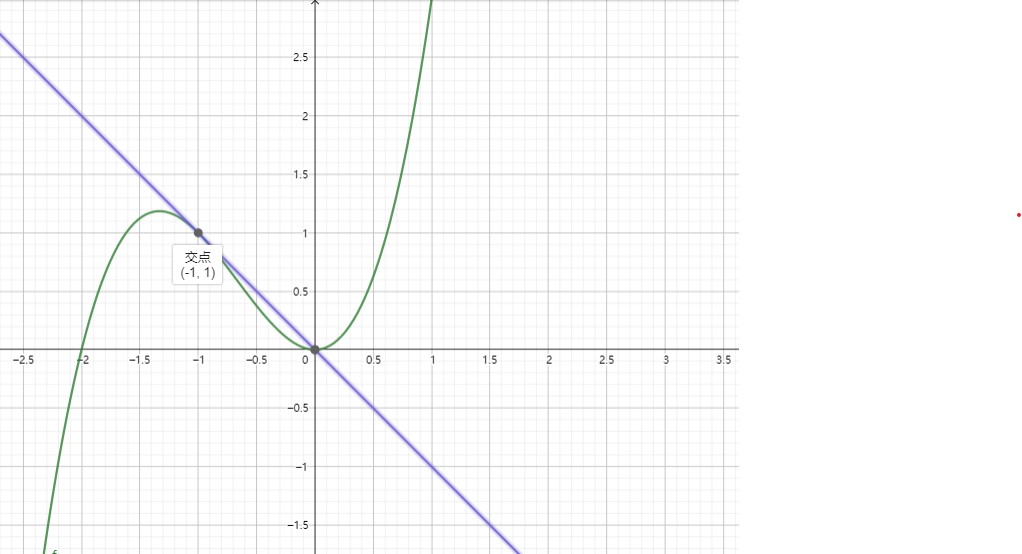
如图，为 \(f(x)=x^3+2x^2\) 于 \((-1, 1)\) 处的切线 \(y=-x\) (导数为 \(-1\))。可见，该点的切线还过函数另一点 \((0, 0)\)。
我不知道如何给出一个规范的定义，暂时也没有查到，查到再补定义的坑吧。（如果有人有好的定义，麻烦评论）
2.3 求法
有了前面“平均变化率”的铺垫，我们可以想到，\(f(x)\) 在 \((x_1, f(x_1))\) 的导数其实可以看成 \(f(x)\) 在 \([x_1, x_1]\) 区间内的平均变化率。
于是尝试计算：\(k = \frac{\Delta y}{\Delta x} = \frac{f(x_1) - f(x_1)}{x - x} = \frac{0}{0} =\) 无意义
经过思考也可以明白，仅知道一条直线（我们要求的切线）所过的一个点的坐标，是不足以算出其斜率或表达式的。
但是，我们不仅知道 \((x_1, f(x_1))\)，还知道 \(f(x)\) 的表达式！
于是历史上一位大牛横空出世，创造了 \(\lim\) 符号。
2.3.1 什么是 lim 符号
对于 $$\lim_{a \rightarrow b}f(a)$$ 来说，其表示的是 \(a\) 在极限接近于 \(b\) 时的值。一般的，这里的 \(a\) 若取了 \(b\)，则 \(f(a)\) 大概率是无意义的。
2.3.2 用 lim 解决我们的问题
（接下来都以 \(f(x)=x^3+2x^2\) 于 \((-1, 1)\) 的切线为例）
我们假设有一条线经过了两个函数上的点 \((x_1, f(x_1))\) 和 \((x_1 + \Delta x, f(x_1 + \Delta x))\)。理想情况是，当 \(\Delta x = 0\) 时，这条线就是过 \((x_1, f(x_1))\) 的函数切线。
[这句话应该用于导函数处，此处应该经过修改]$$\lim_{\Delta x \rightarrow 0} \frac{f(x) - f(x + \Delta x)}{x - (x + \Delta x)} = \lim_{\Delta x \rightarrow 0} {\Delta x \rightarrow 0} \frac{x3+2x2 - ((x + \Delta x)^3+2(x + \Delta x)^2)}{-\Delta x} = \lim_{\Delta x \rightarrow 0} \frac{x3+2x2 - (x3+2x2+3x^2\Delta x+3x\Delta x^2+\Delta x^3+4x\Delta x+\Delta x^2)}{-\Delta x} = \lim_{\Delta x \rightarrow 0} \frac{3x^2\Delta x+3x\Delta x^2+\Delta x^3+4x\Delta +\Delta x^2)}{\Delta x}=\lim_{\Delta x \rightarrow 0} 3x^2+3x\Delta x+\Delta x^2+4x+\Delta x=3x^2+4x$$
要理解上面这个式子，【to be continued】
2.4 应用
For OIers & ACMers: 洛谷习题 数学 1.2.1】导数（非导函数） 【数学 1.2.2】函数的切线
// 未完待续
docu
[这句话应该用于导函数处，此处应该经过修改]$$\lim_{\Delta x \rightarrow 0} \frac{f(x) - f(x + \Delta x)}{x - (x + \Delta x)} = \lim_{\Delta x \rightarrow 0} {\Delta x \rightarrow 0} \frac{x3+2x2 - ((x + \Delta x)^3+2(x + \Delta x)^2)}{-\Delta x} = \lim_{\Delta x \rightarrow 0} \frac{x3+2x2 - (x3+2x2+3x^2\Delta x+3x\Delta x^2+\Delta x^3+4x\Delta x+\Delta x^2)}{-\Delta x} = \lim_{\Delta x \rightarrow 0} \frac{3x^2\Delta x+3x\Delta x^2+\Delta x^3+4x\Delta +\Delta x^2)}{\Delta x}=\lim_{\Delta x \rightarrow 0} 3x^2+3x\Delta x+\Delta x^2+4x+\Delta x=3x^2+4x$$
