图论进阶
LCA、树上前缀和与差分
LCA
LCA 指的是树上最长公共祖先,我们可以现想出一个 预处理 \(\mathcal O (N^2)\), 单次查询 \(\mathcal O(N)\) 的做法:
令 f[i][j] 为 i 的第 j 层祖先是那个节点,因而有转移式:
f[i][j]=f[fa[i]][j-1],我们便可以直接推出结果。
然后我们对这个进行倍增优化,令 g[i][j] = f[i][1<<j],因而可以得出新的转移式:
g[i][j]=g[g[i][j-1]][j-1],及时间复杂度为 \(\mathcal O(N\log N+Q\log N)\)。
CODE:
template<int N>
class LCA{
private:
int dep[N];
int fa[N][21];
public:
void build(int x=root,int f=0){
dep[x]=dep[f]+1;
fa[x][0]=f;
for(int i=1;i<=20;i++)
fa[x][i]=fa[fa[x][i-1]][i-1];
for(auto y: v[x]){
if(y==f) continue;
build(y,x);
}
}
int lca(int x,int y){
if(dep[x]<dep[y]) swap(x,y);
for(int i=20;i>=0;i--){
if(dep[fa[x][i]]>=dep[y])
x=fa[x][i];
}
if(x==y) return x;
for(int i=20;i>=0;i--){
if(fa[x][i]!=fa[y][i])
x=fa[x][i],y=fa[y][i];
}
return fa[x][0];
}
};
LCA<N> L;
本做法比正常做法 man 100ms,加不加 template 都一样。
树上前缀和
先明确我们所要解决的问题:
有一颗有多个带边权的无向边组成树
现在查询多次两个点之间的距离。
我们先定义一个点的前缀和 sum[] 为这个点到根节点的路径长度。
于是 x 到 y 的距离为 sum[x]+sum[y]-2*sum[lca[x,y]]。
如果是处理点的同理。
CODE:就不挂了
树上差分
先明确我们所要解决的问题:
有一颗初始点权都为 0 的树,有多次操作每一次给一条路径上的点都加
x然后最后询问你每一个点的点权
我们先定义一个树的差分数组 d[x] = val[x]-val[fa[x]], 因而,当给 x 到 y 的路径处理时:
d[fa[x]]++,d[x]--,d[y]--
然后在最后求一个前缀和即可。
如果是处理边的同理。
CODE:就不挂了
DFS 序与树链剖分
先感谢以前自己居然写了总结,I love char
但是,什么垃圾 latex
DFS 序
DFS 序,就是对于一个图进行 DFS 便利时,访问节点的顺序
如下图:
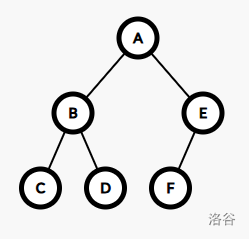
这棵树的 DFS 序是 A B C D E F
那这又有什么用呢?
当我们要计算以 B 为根的字数点权和时,相当于是求 A+B+C, 这样正好在 DFS 序中构成了一个区间。
如 [dfn[x],dfn[x]+siz[x]-1], 相当于将 树上便利 变为了 区间修改,于是可以使用数据结构来维护。
树链剖分
对于一个要进行树链剖分的树,有以下定义:
- 重子节点:儿子中子树最大的节点
- 轻子节点:其他节点
- 重边:向下连接到重子节点的边
- 轻边:其他边
- 重链:由重边相连组成的链
(如下图)

因而我们需要记录以下信息:
fa[x]父亲节点dep[x]深度siz[x]子树大小son[x]重儿子top[x]所在重链的顶部节点dfn[x]DFS 序
很明显而发现,每一个点都会属于一个重链,或者说,整棵树被分成了若干条链
更明显 能发现,轻子节点的子树大小小于父亲节点子树大小的一半
同时也 显然,任意一条最短路径可以被分成了至多 \(\log n\) 条重链
证明:
我们可以将这条链分为按 LCA 分界的两条链,设其中一条链会被分成 \(k\) 段,则这条链上一定有 \(k\) 个轻节点,有上一个结论:
轻子节点的子树大小小于父亲节点子树大小的一半可以发现,这条链的尾部节点子树大小最多为 \(\frac{lca子树大小}{2^k}\),lca 子树大小最多为 \(n\),且这条链的尾部节点子树大小最少为 \(1\),因而 \(2^k\) 最大为 \(n\),因而 \(k<\log n\)
那这又有什么用呢?
如果我们要求解一条路径的点权和,便可以转换为求解若干条重链,我们发现一个节点只有一个重子节点,因而只需要每一次先枚举重子节点,便可保证每条重链的 DFS 序是连续的,即可用 \(\log n\) 的时间复杂度求解每一条重链的点权和。
那么如何拆分重链
这种过程有点类似 LCA,但是每一次是从 \(x\) 跳到 fa[top[x]], 且结束条件为两点在同一重链上,步骤:
- 检测两个点的
top是否相等,如果是,跳出循环 - 如果
top[x]的深度小于top[y]的深度,交换,及每一次跳矮的。 - 对于从线段树
[dfn[x],dfn[fa[top[x]]]寻找答案 - 更新 \(x\) 为
fa[top[x]] - 回到 1
- 处理线段树
[dfn[x],dfn[y]]
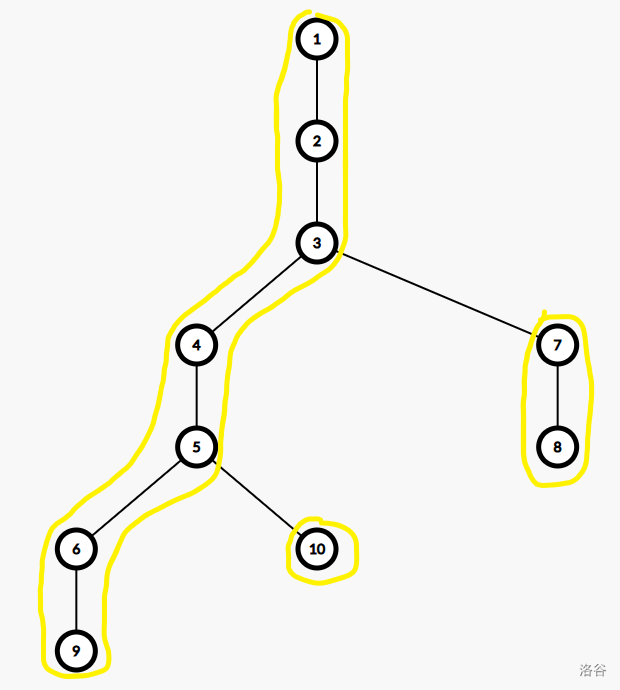
如图,当求 (10,8) 时,10 --> 5,8 -> 3 然后算 [5,3]。
CODE
DFS 预处理:
-
build1:
fa[],dep[],siz[],son[]。 -
build2:
top[],dfn[]。
代码:
void build1(int x,int ff){
son[x]=-1,siz[x]=1;
for(int i=head[x];i;i=nxt[i]){
int y=ver[i];
if(y==ff) continue;
dep[y]=dep[x]+1;
fa[y]=x;
build1(y,x);
siz[x]+=siz[y];
if(son[x]==-1||siz[y]>siz[son[x]]) son[x]=y;
}
}
void build2(int x,int ff,int tp){
top[x]=tp;
dfn[x]=++cnt;
rnk[cnt]=x;
if(son[x]==-1) return;
build2(son[x],x,tp);
for(int i=head[x];i;i=nxt[i]){
int y=ver[i];
if(y==ff||y==son[x]) continue;
build2(y,x,y);
}
}
从 x 到 y 结点最短路径上所有节点的值都加上 z
void update(int x,int y,int k){
k%=P;
while(top[x]!=top[y]){
if(dep[top[x]]<dep[top[y]]) swap(x,y);
change(1,dfn[top[x]],dfn[x],k);
x=fa[top[x]];
}
if(dep[x]>dep[y]) swap(x,y);
change(1,dfn[x],dfn[y],k);
}
求树从 x 到 y 结点最短路径上所有节点的值之和
int query(int x,int y){
int ans=0;
while(top[x]!=top[y]){
if(dep[top[x]]<dep[top[y]]) swap(x,y);
ans+=ask(1,dfn[top[x]],dfn[x]);
ans%=P;
x=fa[top[x]];
}
if(dep[x]>dep[y]) swap(x,y);
ans+=ask(1,dfn[x],dfn[y]);
ans%=P;
return ans;
}
将以 x 为根节点的子树内所有节点值都加上 z
void updatetree(int x,int k){
change(1,dfn[x],dfn[x]+siz[x]-1,k);
}
求以 x 为根节点的子树内所有节点值之和
int querytree(int x){
return ask(1,dfn[x],dfn[x]+siz[x]-1);
}
CODE:
int cnt,rnk[N],a[N];//DFS序,初始点权
int fa[N],dep[N],siz[N],son[N],top[N],dfn[N];//点的信息
class SMT{
private:
struct SegmentTree{
int l,r;//左右端点
int sum;//区间和
int tag;//区间懒标记
#define lc p<<1
#define rc p<<1|1
}T[N<<2];
void push_down(int p){
if(T[p].tag==0) return;
T[lc].sum=(T[lc].sum+T[p].tag*(T[lc].r-T[lc].l+1))%P;
T[rc].sum=(T[rc].sum+T[p].tag*(T[rc].r-T[rc].l+1))%P;
T[lc].tag=(T[lc].tag+T[p].tag)%P;
T[rc].tag=(T[rc].tag+T[p].tag)%P;
T[p].tag=0;
}
public:
void build(int p,int l,int r){
T[p].l=l,T[p].r=r;
if(l==r) {
T[p].sum=a[rnk[l]];
return;
}
int mid=l+r>>1;
build(lc,l,mid);
build(rc,mid+1,r);
T[p].sum=(T[lc].sum+T[rc].sum)%P;
}
void change(int p,int l,int r,int k){
if(l<=T[p].l && r>=T[p].r){
T[p].sum+=(T[p].r-T[p].l+1)*k;
T[p].sum%=P;
T[p].tag+=k;
T[p].tag%=P;
return;
}
push_down(p);
int mid=T[p].l+T[p].r>>1;
if(l<=mid) change(lc,l,r,k);
if(r>mid) change(rc,l,r,k);
T[p].sum=T[lc].sum+T[rc].sum;
T[p].sum%=P;
}
int ask(int p,int l,int r){
if(l<=T[p].l && r>=T[p].r){
return T[p].sum;
}
push_down(p);
int ans=0;
int mid=T[p].l+T[p].r>>1;
if(l<=mid) ans+=ask(lc,l,r);
if(r>mid) ans+=ask(rc,l,r);
ans%=P;
return ans;
}
};
SMT T;
void build1(int x,int f){
son[x]=-1,siz[x]=1;
for(auto y: v[x]){
if(y==f) continue;
dep[y]=dep[x]+1;
fa[y]=x;
build1(y,x);
siz[x]+=siz[y];
if(son[x]==-1||siz[y]>siz[son[x]]) son[x]=y;
}
}
void build2(int x,int f,int tp){
top[x]=tp;
dfn[x]=++cnt;
rnk[cnt]=x;
if(son[x]==-1) return;
build2(son[x],x,tp);
for(auto y: v[x]){
if(y==f||y==son[x]) continue;
build2(y,x,y);
}
}
int query(int x,int y){
int ans=0;
while(top[x]!=top[y]){
if(dep[top[x]]<dep[top[y]]) swap(x,y);
ans+=T.ask(1,dfn[top[x]],dfn[x]);
ans%=P;
x=fa[top[x]];
}
if(dep[x]>dep[y]) swap(x,y);
ans+=T.ask(1,dfn[x],dfn[y]);
ans%=P;
return ans;
}
void update(int x,int y,int k){
k%=P;
while(top[x]!=top[y]){
if(dep[top[x]]<dep[top[y]]) swap(x,y);
T.change(1,dfn[top[x]],dfn[x],k);
x=fa[top[x]];
}
if(dep[x]>dep[y]) swap(x,y);
T.change(1,dfn[x],dfn[y],k);
}
int querytree(int x){
return T.ask(1,dfn[x],dfn[x]+siz[x]-1);
}
void updatetree(int x,int k){
T.change(1,dfn[x],dfn[x]+siz[x]-1,k);
}
T.build(1,1,n)
build1(root,0);
build2(root,0,root);
最段路 与 MST
差分约束
依然是先明确问题类型:
有
n个待定的树a[],要求满足m组操作满足:
a[i]-a[j] <= k每组i,j,k在变化现在询问你是否有一组解
a[],满足上述要求。
首先我们可以将问题转换为图论问题,当我们 add(u,v,w), 及满足 a[v]-a[u]<=w
当我们同时观察两条头尾相接的边时,则有 add(x,y,w1), add(y,z,w2),既满足 a[y]-a[x]+a[z]-a[y] <= w1+w2。
及:a[z]-a[x] <= w1+w2。
当我们令 a[0]=inf,add(0,x,0) 时,显然可以直接计算 0 到每一个点 x 的 最段路 然后令 a[x] = dis,可以证明,此时 a[x] 最大。
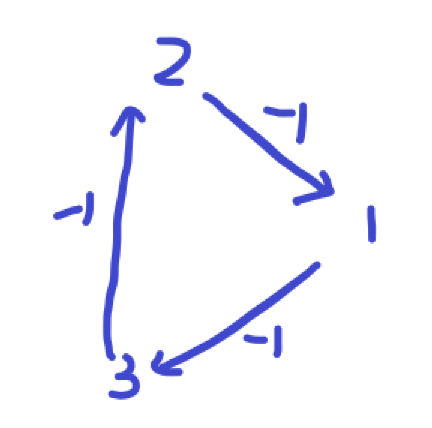
但是如果路径中出现负环(如下),则一定无解:
对于下面这组
a[2]-a[1] >= 1 a[3]-a[2] >= 1 a[1]-a[3] >= 1会连成:(未画 0 )
其中出现了负环
因此我们只需要判断一下图中是否有负环即可,可以用 spfa。
CODE:
#include<bits/stdc++.h>
using namespace std;
/*!@#$%^&*!@#$%^&*~~优美的分界线~~*&^%$#@!*&^%$#@!*/
const int N=1e4+5;
int n,m1,m2;
int dis[N],vis[N],cnt[N];
int tot,head[N],nxt[N<<1],ver[N<<1],edg[N<<1];
/*!@#$%^&*!@#$%^&*~~优美的分界线~~*&^%$#@!*&^%$#@!*/
void add_edg(int a,int b,int c){
ver[++tot]=b,edg[tot]=c;
nxt[tot]=head[a],head[a]=tot;
}
int spfa(int start){
queue<int> Q;
Q.push(start);
memset(vis,0,sizeof vis);
memset(cnt,0,sizeof cnt);
memset(dis,0x3f,sizeof dis);
dis[start]=0,vis[start]=1;
while(!Q.empty()){
int x=Q.front();Q.pop();
vis[x]=0,cnt[x]++;
for(int i=head[x];i;i=nxt[i]){
int y=ver[i],w=edg[i];
if(cnt[y]>n) return -1;//有负环
if(dis[y]>dis[x]+w){
dis[y]=dis[x]+w;
if(vis[y]==0){
Q.push(y);
vis[y]=1;
}
}
}
}
if(dis[n]>=0x3f3f3f3f) return -2;
else return dis[n];
}
/*!@#$%^&*!@#$%^&*~~优美的分界线~~*&^%$#@!*&^%$#@!*/
signed main(){
cin>>n>>m1>>m2;
while(m1--){
int a,b,d;cin>>a>>b>>d;
add_edg(a,b,d);
}
while(m2--){
int a,b,d;cin>>a>>b>>d;
add_edg(b,a,-d);
}
for(int i=1;i<=n;i++) add_edg(0,i,0);
for(int i=1;i<n;i++) add_edg(i+1,i,0);
if(spfa(0)<=-1) cout<<spfa(0);
else{
cout<<spfa(1);
}
return 0;
}
Tarjan
这里给出 dfn[] 的定义。
dfn[]为图遍历时的时间辍。
这里在给出 low[] 的定义:
low[x]为下面可选节点的时间辍的最小值。
x子树中的节点- 通过一条不再搜索树上的节电,能够到达
x的子树的介电节点。及:
对于节点
x的相邻节点y:
low[x]=dfn[x]- 若
x是y的搜索树上的父节点:low[x]=min(low[x],low[y])- 边
(x,y)不是搜索树上边:low[x]=min(low[x],dfn[x])
无向图联通性
判割点
定义
对于一个无向连通图,如果一个点去掉之后,会分裂成多个联通块,则称这个
做法
先给出结论,对于一个节点 x,如果有 x 的子节点 y:
dfn[x]<=low[y]
则 x 为割点。
证明
如下图:
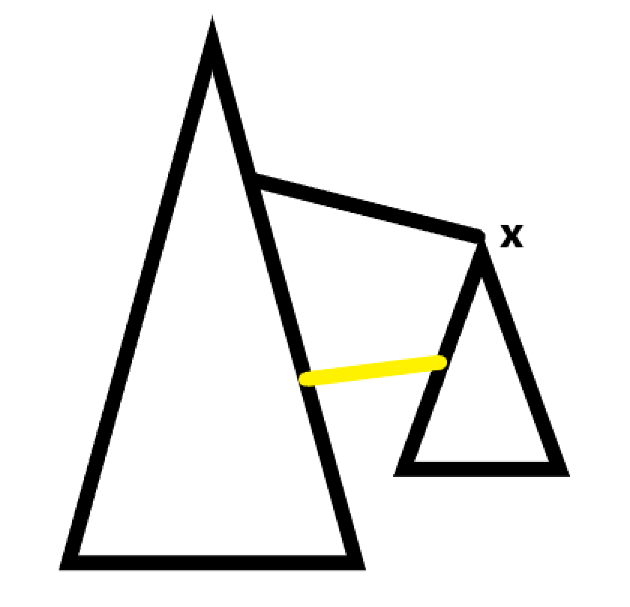
如果 X 不是割点,则一定没有黄色的这条边,则 low[x]<=dfn[y]。
这里因为是 <=,所以可以不用考虑访问到父亲节点的问题,而下面的割边则不同。
CODE:
void Tarjan(int x){
dfn[x]=low[x]=++idx;
int flag=0;
for(int i=head[x];i;i=nxt[i]){
int y=ver[i];
if(!dfn[y]){
Tarjan(y);
low[x]=min(low[x],low[y]);
if(low[y]>=dfn[x]){
flag++;
if(x!=root||flag>1)
cnt[x]=1;
}
}else
low[x]=min(low[x],dfn[y]);
}
}
for(int i=1;i<=n;i++){
if(!dfn[i]){
root=i;
Tarjan(i);
}
}
求割边
对于边 e, 如果删除这条边后,图中出现了多个不相邻的子图,则称 x 为这个图的割边。
易证,当存在一个 x 的子节点 y 满足:dfn[x] < low[y]。
需要注意的是我们需要盘是否原路返回(不算重边)
CODE:
int tot=1;
void add(int a,int b){
ver[++tot]=b;
nxt[tot]=head[a],head[a]=tot;
}
void Tarjan(int x,int edge){
dfn[x]=low[x]=++idx;
for(int i=head[x];i;i=nxt[i]){
int y=ver[i];
if(!dfn[y]){
Tarjan(y,i);
low[x]=min(low[x],low[y]);
if(low[y]>dfn[x])
c[++iteam]={x,y};
}else if(i!=(edge^1))
low[x]=min(low[x],dfn[y]);
}
}
for(int i=1;i<=n;i++){
if(!dfn[i]){
root=i;
Tarjan(i,0);
}
}
双连通分量
定义:(来自 OI-Wiki)
在一张连通的无向图中,对于两个点 𝑢
和 𝑣
,如果无论删去哪条边(只能删去一条)都不能使它们不连通,我们就说 𝑢
和 𝑣
边双连通。
在一张连通的无向图中,对于两个点 𝑢
和 𝑣
,如果无论删去哪个点(只能删去一个,且不能删 𝑢
和 𝑣
自己)都不能使它们不连通,我们就说 𝑢
和 𝑣
点双连通。
边双连通具有传递性,即,若 𝑥,𝑦
边双连通,𝑦,𝑧
边双连通,则 𝑥,𝑧
边双连通。
点双连通 不 具有传递性,反例如下图,𝐴,𝐵
点双连通,𝐵,𝐶
点双连通,而 𝐴,𝐶
不 点双连通。
对于一个无向图中的 极大 边双连通的子图,我们称这个子图为一个 边双连通分量。
对于一个无向图中的 极大 点双连通的子图,我们称这个子图为一个 点双连通分量。
CODE:(v-DCC)
因为我们发现两个 v-DCC 重叠的区域一定是一个割点,所以我们只需要在求割点的代码内加入一个出入栈,记录的过程即可。
void Tarjan(int x){
dfn[x]=low[x]=++idx;
st[++top]=x;
if(!head[x]){
v[++cnt].push_back(x);
return;
}
for(int i=head[x];i;i=nxt[i]){
int y=ver[i];
if(!dfn[y]){
Tarjan(y);
low[x]=min(low[x],low[y]);
if(low[y]>=dfn[x]){
int z;cnt++;
while(1){
z=st[top--];
vdcc[z]=cnt;
v[cnt].push_back(z);
if(z==y) break;
}
v[cnt].push_back(x);
}
}else
low[x]=min(low[x],dfn[y]);
}
}
CODE:(e-DCC)
我们发现 e-DCC,我们发现如果 dfn[x] = low[x], 及 x 本身即是 x 的搜索子树可达到的 DFS 序 最小的节点。
这是除去以前已经分配了的元素,剩下在栈里面的一定是一个 e-DCC。
但是我们可以发现 e-DCC 其实就是除去了所有的割边后留下的连通块,也可以先处理完割边在处理。
void Tarjan(int x,int edge){
dfn[x]=low[x]=++idx;
st[++top]=x;
for(int i=head[x];i;i=nxt[i]){
int y=ver[i];
if(!dfn[y]){
Tarjan(y,i);
low[x]=min(low[x],low[y]);
}else if(i!=(edge^1))
low[x]=min(low[x],dfn[y]);
}
if(dfn[x]==low[x]){
int y;cnt++;
do{
y=st[top--];
edcc[y]=cnt;
v[cnt].push_back(y);
}while(x!=y);
}
}
有向图的连通性
强连通分量
对于一个有向图,如果其中每两个点都可以互相到达,则称这个图为强连通图。
而一个有向图的子图如果是强连通图,则称这个子图为强连通分量
做法和前面的差不多,满足条件 dfn[x] = dfn[y]。
如下图,图中黄色,红色的边都会使 low[x] < dfn[x],
因而这个中间的节点一定不是他所在的 scc 的最先访问的节点。
因而把当前在栈里面的元素都标记一下即可

void Tarjan(int x){
dfn[x]=low[x]=++idx;
ins[x]=1;
st[++top]=x;
for(int i=head[x];i;i=nxt[i]){
int y=ver[i];
if(!dfn[y]){
Tarjan(y);
low[x]=min(low[x],low[y]);
}else if(ins[y])
low[x]=min(low[x],dfn[y]);
}
if(dfn[x]==low[x]){
int y;cnt++;
do{
y=st[top--];
scc[y]=cnt;
ins[y]=0;
siz[cnt]++;
b[cnt]+=a[y];
}while(y!=x);
}
}
缩点
有向图的缩点我觉得用处十分的大,因为它可以用来解决 2 - SAT 问题,当然代码和无向图的缩点差不多:
for(int x=1;x<=n;x++){
for(int i=head[x];i;i=nxt[i]){
int y=ver[i];
if(scc[x]==scc[y]) continue;
v[scc[x]].push_back(scc[y]);
d[scc[y]]++;
}
}
2 - SAT 适定性问题
解决问题可食用范围
有 n 个非 0 及 1 的变量 a[i],满足以下 m 个条件:
如果
a[i]为x,则a[j]为y。
解决思路
我们仍然要先将其转化为 图论问题,首先我们把每一个 a[i] 分成两个点:i,i+n,表示 a[i] = 0,a[i] = 1。
对于一条边 (u,v),表示如果 u%n 为 u/n 则 v%n 为 v/n。
然后我们就可以建出一个有向图。
4 8
1 0 2 1
4 0 2 1
3 0 1 1
1 1 3 1
3 1 4 1
4 1 1 1
2 0 3 1
2 1 3 0
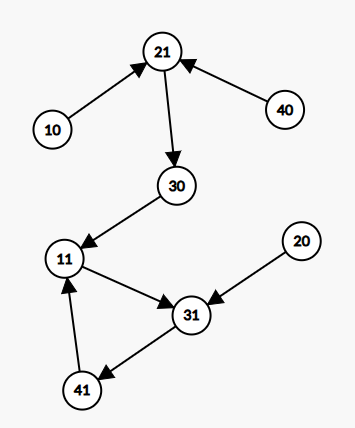
我们可以发现:
-
如果两个属于同一元素的节点在一条链上时,越靠近末尾的就是答案。
-
且对于在一个
scc内的元素,他们要不是同时满足,要不是都不满足,所以如果同一元素的两个点在一个scc中,一定无解 -
拓扑排序值越大则约有可能
那肯定有 聪明的小朋友们 发现了,这样模拟上面的图,答案是 1 1 1 1 ,这也不对啊,答案是这个图画错了
我们知道如果:
则称 \(p\) 为 \(q\) 的充分条件,\(q\) 为 \(p\) 的必要条件,因而满足:
所以我们把这样的几条边连上:
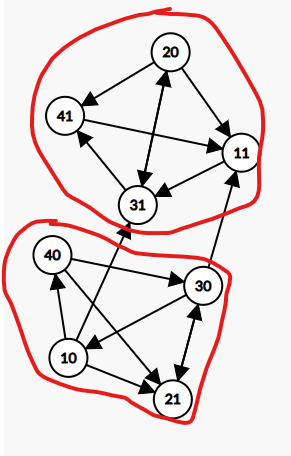
就只有两个 scc 了,我们显然要满足上面的,及答案为 1011。
所以我们不仅要连正边,也要连反边。
CODE:
#include<bits/stdc++.h>
using namespace std;
/*!@#$%^&*!@#$%^&*~~优美的分界线~~*&^%$#@!*&^%$#@!*/
const int N=4e6+5,M=4e6+5;
int n,m;
int ins[N];
int st[N],top;
int cnt,edcc[N];
int idx,dfn[N],low[N];
int tot=1,head[N],ver[M<<1],nxt[M<<1];
/*!@#$%^&*!@#$%^&*~~优美的分界线~~*&^%$#@!*&^%$#@!*/
void add(int a,int b){
ver[++tot]=b;
nxt[tot]=head[a],head[a]=tot;
}
void Tarjan(int x){
dfn[x]=low[x]=++idx;
st[++top]=x,ins[x]=1;
for(int i=head[x];i;i=nxt[i]){
int y=ver[i];
if(!dfn[y]){
Tarjan(y);
low[x]=min(low[x],low[y]);
}else if(ins[y])
low[x]=min(low[x],dfn[y]);
}
if(dfn[x]==low[x]){
int y;cnt++;
do{
y=st[top--];
edcc[y]=cnt;
ins[y]=0;
}while(y!=x);
}
}
/*!@#$%^&*!@#$%^&*~~优美的分界线~~*&^%$#@!*&^%$#@!*/
signed main(){
cin>>n>>m;
while(m--){
int i,a,b,j;
cin>>a>>i>>b>>j;
add(a+(n*i),b+(n*j));
add(b+(n*(j^1)),a+(n*(i^1)));
}
for(int i=1;i<=2*n;i++)
if(!dfn[i])
Tarjan(i);
for(int i=1;i<=n;i++)
if(edcc[i]==edcc[i+n]){
cout<<"IMPOSSIBLE";
return 0;
}
cout<<"POSSIBLE\n";
for(int i=1;i<=n;i++) cout<<(edcc[i]>edcc[i+n])<<' ';
return 0;
}
/*这个代码并非 P4782 【模板】2-SAT*/
扩展
一般的题问你是否有解,或者有 SPJ。
如果需要你判断不确定,就需要用上面的判断是否在一条链上,否则不知道:
#include<bits/stdc++.h>
using namespace std;
/*!@#$%^&*!@#$%^&*~~优美的分界线~~*&^%$#@!*&^%$#@!*/
const int N=4005,M=10005;
int n,m;
int d[N];
int vis[N];
int dis[N];
int ins[N];
int st[N],top;
int cnt,scc[N];
int idx,dfn[N],low[N];
int tot,head[N],ver[M<<1],nxt[M<<1];
vector<int> v[N];
/*!@#$%^&*!@#$%^&*~~优美的分界线~~*&^%$#@!*&^%$#@!*/
void add(int a,int b){
ver[++tot]=b;
nxt[tot]=head[a],head[a]=tot;
}
void Tarjan(int x){
dfn[x]=low[x]=++idx;
st[++top]=x,ins[x]=1;
for(int i=head[x];i;i=nxt[i]){
int y=ver[i];
if(!dfn[y]){
Tarjan(y);
low[x]=min(low[x],low[y]);
}else if(ins[y])
low[x]=min(low[x],dfn[y]);
}
if(dfn[x]==low[x]){
int y;cnt++;
do{
y=st[top--];
scc[y]=cnt;
ins[y]=0;
}while(y!=x);
}
}
void dfs(int x,int fa){
vis[x]=1;
for(int i=head[x];i;i=nxt[i]){
int y=ver[i];
if(vis[y]) continue;
dfs(y,x);
}
}
bool check(int x){
memset(vis,0,sizeof vis);
dfs(x,0);
for(int i=1;i<=n;i++)
if(vis[i]&&vis[i+n])
return 0;
return 1;
}
/*!@#$%^&*!@#$%^&*~~优美的分界线~~*&^%$#@!*&^%$#@!*/
signed main(){
ios::sync_with_stdio(0);
cin.tie(0),cout.tie(0);
cin>>n>>m;
for(int i=1;i<=m;i++){
int a,b;char c,d;
cin>>a>>c>>b>>d;
int p1=(c=='Y'),p2=(d=='Y');
add(a+n*(p1^1),b+n*p2);
add(b+n*(p2^1),a+n*p1);
}
for(int i=1;i<=2*n;i++)
if(!dfn[i])
Tarjan(i);
for(int i=1;i<=n;i++)
if(scc[i]==scc[i+n]){
cout<<"IMPOSSIBLE";
return 0;
}
for(int x=1;x<=2*n;x++){
for(int i=head[x];i;i=nxt[i]){
int y=ver[i];
if(scc[x]==scc[y]) continue;
v[scc[x]].push_back(scc[y]);
d[scc[y]]=0;
}
}
for(int i=1;i<=n;i++){
if(check(i)&&check(i+n)) cout<<'?';
else if(scc[i]<scc[i+n]) cout<<'N';
else cout<<'Y';
}
return 0;
}
注意会退化为 \(\mathcal O(N^2)\)
二分图匹配
什么是二分图
二分图是一个没有奇环的图
这是因为二分图的点要分为左部和右部,而边只能连接左部和右部。
如果要回到原点,必然走偶数次,我们可以用染色法判断
void dfs(int x,int val){
vis[x]=val;
for(int i=0;i<v[x].size();i++){
int y=v[x][i];
if(vis[y]==0) dfs(y,3-val);
else if(vis[y]==val)
flag=1;
}
}
for(int i=1;i<=n;i++)
if(!vis[i])
dfs(i,1);
cout<<(flag?"No":"Yes");
二分图最大匹配
匹配指的是一个边的集合,使其两两不公用节点。
我们发现所有的边可以连成多条链,且每一条必定为一个 10101010101 的匹配串,且我们可以尝试对匹配串取反
比如:
1+1010101
= 1+0101010
= 10101010
这样虽然答案不一定会增加,但不减少。
因而记录一下 match[] 为右边匹配左边,一直往前跳并取反。
bool dfs(int x){
for(int i=head[x];i;i=nxt[i]){
int y=ver[i];
if(!vis[y]){
vis[y]=1;
if(match[y]==-1||dfs(match[y])){
match[y]=x;
return 1;
}
}
}
return 0;
}
int ans=0;
memset(match,-1,sizeof match);
for(int i=1;i<=n;i++){
memset(vis,0,sizeof vis);
if(dfs(i)) ans++;
}
cout<<ans<<'\n';
时间复杂度:\(\mathcal O(NM)\)。
应用
一般是一个位置对应一个答案,然后连接后跑二分图
如这道题:P1963 变换序列 - 洛谷
我们对每一个 i 连上 i+d,i-d,i-(n-d),i+(n-d)。
然后直接跑二分图:
CODE:
#include<bits/stdc++.h>
using namespace std;
/*!@#$%^&*!@#$%^&*~~优美的分界线~~*&^%$#@!*&^%$#@!*/
const int N=1e4+5,M=2e5+5;
int n;
int a[N];
int ans[N];
int match[N],vis[N];
int tot,head[N],nxt[M],ver[M];
/*!@#$%^&*!@#$%^&*~~优美的分界线~~*&^%$#@!*&^%$#@!*/
void add(int a,int b){
ver[++tot]=b;
nxt[tot]=head[a],head[a]=tot;
}
bool dfs(int x){
for(int i=head[x];i;i=nxt[i]){
int y=ver[i];
if(!vis[y]){
vis[y]=1;
if(match[y]==-1||dfs(match[y])){
match[y]=x;
ans[x]=y;
return 1;
}
}
}
return 0;
}
/*!@#$%^&*!@#$%^&*~~优美的分界线~~*&^%$#@!*&^%$#@!*/
signed main(){
cin>>n;
for(int i=0;i<n;i++){
int x;cin>>x;
int a[4]={-1,-1,-1,-1};
if(i-x>=0) a[0]=i-x;
if(i+x<n) a[1]=i+x;
if(x!=n-x){
if(i-(n-x)>=0) a[2]=i-(n-x);
if(i+(n-x)<n) a[3]=i+(n-x);
}
sort(a,a+4);
for(int j=3;j>=0;j--)
if(a[j]!=-1)
add(i,a[j]);
}
memset(match,-1,sizeof match);
for(int i=n-1;i>=0;i--){
memset(vis,0,sizeof vis);
if(!dfs(i)){
cout<<"No Answer";
return 0;
}
}
for(int i=0;i<n;i++)
cout<<ans[i]<<' ';
return 0;
}
基环树
基环树 本质上就是在树上多了一条边。
而 基环树森林 本质上就是在每一颗树上多了一条边
基环树 问题有两种解决思路:
拆边
我们先找到那个环上的一条边,然后将其删去,按照树的方式处理。
最后在把边加上合并
像是这道题:P2607 骑士 - 洛谷
我们先把那多出来的一条边删除,然后以两个点位根跑树上 DP。
重要的是如何合并,我们需要考虑这条边的两个点选货不选的情况,最后合并最大值:
CODE:
#include<bits/stdc++.h>
#define int long long
#define PII pair<int,int>
using namespace std;
/*!@#$%^&*!@#$%^&*~~优美的分界线~~*&^%$#@!*&^%$#@!*/
const int N=4e6+5;
int n;
int cnt;
int c[N];
int f[N][2];
int fa[N];
PII l[N];
int tot,head[N],nxt[N<<1],ver[N<<1];
/*!@#$%^&*!@#$%^&*~~优美的分界线~~*&^%$#@!*&^%$#@!*/
void add(int a,int b){
ver[++tot]=b;
nxt[tot]=head[a],head[a]=tot;
}
int find(int x){
if(x==fa[x]) return x;
return fa[x]=find(fa[x]);
}
void dfs(int x,int fa,int t){//表示to这个点的骑士不能参见骑士团
f[x][0]=0;
if(x==t) f[x][1]=-0x3f3f3f3f;
else f[x][1]=c[x];
for(int i=head[x];i;i=nxt[i]){
int y=ver[i];
if(y==fa) continue;
dfs(y,x,t);
f[x][0]+=max(f[y][0],f[y][1]);
if(x!=t) f[x][1]+=f[y][0];
}
}
/*!@#$%^&*!@#$%^&*~~优美的分界线~~*&^%$#@!*&^%$#@!*/
signed main(){
ios::sync_with_stdio(0);
cin.tie(0),cout.tie(0);
cin>>n;
for(int i=1;i<=n;i++)
fa[i]=i;
for(int i=1;i<=n;i++){
int a,b;cin>>a>>b;
c[i]=a;
int xa=find(i),xb=find(b);
if(xa==xb)
l[++cnt]=make_pair(i,b);
else
add(i,b),add(b,i);
fa[xa]=xb;
}
int ANS=0;
for(int i=1;i<=cnt;i++){
int ans=0;
dfs(l[i].first,-1,-1);
ans=f[l[i].first][0];
dfs(l[i].first,-1,l[i].second);
ans=max(ans,max(f[l[i].first][0],f[l[i].first][1]));
ANS+=ans;
}
cout<<ANS;
return 0;
}
留下环
像是下面这个图
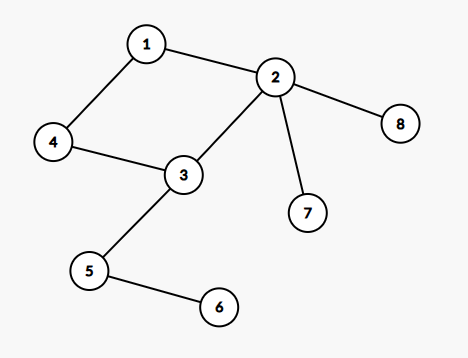
我们把他想象成一个环上挂着很多课树,最后直接合并。



 浙公网安备 33010602011771号
浙公网安备 33010602011771号