基础算法总结
说点大家知道的
位运算
二进制状态压缩
- 第 k 位:
(n>>k)&1 - 第 0 ~ k-1 位:
n&((1<<k)-1) - 将第 k 位取反:
n xor (1<<k) - 将第 k 位设为 1:
n|(1<<k) - 将第 k 位设为 0:
n&(~(1<<k))
成对变换
对于 n 为奇数, n xor 1 = x-1
对于 n 为偶数, n xor 1 = x+1
因此我们可以将 (0,1) , (2,3) ··· 为一对。
lowbit 运算
lowbit(n) = n&(~n+1) = n&(-n)
实际意义:
找出二进制下第一个是1的位置。
lowbit(0b1011011000) = 1000
运算优先级
| 优先级 | 运算符 | 名称或含义 | 使用形式 | 结合方向 | 说明 |
|---|---|---|---|---|---|
| 1 | [] | 数组下标 | 数组名[常量表达式] | 左到右 | |
| () | 圆括号 | (表达式) 函数名(形参表) | |||
| . | 成员选择(对象) | 对象.成员名 | |||
| -> | 成员选择(指针) | 对象指针->成员名 | |||
| 2 | - | 负号运算符 | -表达式 | 右到左 | 单目运算符 |
| (类型) | 强制类型转换 | (数据类型)表达式 | |||
| ++ | 自增运算符 | ++变量名 变量名++ | 单目运算符 | ||
| -- | 自减运算符 | --变量名 变量名-- | 单目运算符 | ||
| * | 取值运算符 | *指针变量 | 单目运算符 | ||
| & | 取地址运算符 | &变量名 | 单目运算符 | ||
| ! | 逻辑非运算符 | !表达式 | 单目运算符 | ||
| ~ | 按位取反运算符 | ~表达式 | 单目运算符 | ||
| sizeof | 长度运算符 | sizeof(表达式) | |||
| 3 | / | 除 | 表达式 / 表达式 | 左到右 | 双目运算符 |
| * | 乘 | 表达式*表达式 | 双目运算符 | ||
| % | 余数(取模) | 整型表达式%整型表达式 | 双目运算符 | ||
| 4 | + | 加 | 表达式+表达式 | 左到右 | 双目运算符 |
| - | 减 | 表达式-表达式 | 双目运算符 | ||
| 5 | << | 左移 | 变量<<表达式 | 左到右 | 双目运算符 |
| >> | 右移 | 变量>>表达式 | 双目运算符 | ||
| 6 | > | 大于 | 表达式>表达式 | 左到右 | 双目运算符 |
| >= | 大于等于 | 表达式>=表达式 | 双目运算符 | ||
| < | 小于 | 表达式<表达式 | 双目运算符 | ||
| <= | 小于等于 | 表达式<=表达式 | 双目运算符 | ||
| 7 | == | 等于 | 表达式==表达式 | 左到右 | 双目运算符 |
| != | 不等于 | 表达式!= 表达式 | 双目运算符 | ||
| 8 | & | 按位与 | 表达式&表达式 | 左到右 | 双目运算符 |
| 9 | ^ | 按位异或 | 表达式^表达式 | 左到右 | 双目运算符 |
| 10 | | | 按位或 | 表达式|表达式 | 左到右 | 双目运算符 |
| 11 | && | 逻辑与 | 表达式&&表达式 | 左到右 | 双目运算符 |
| 12 | || | 逻辑或 | 表达式||表达式 | 左到右 | 双目运算符 |
| 13 | ?: | 条件运算符 | 表达式1? 表达式2: 表达式3 | 右到左 | 三目运算符 |
| 14 | = | 赋值运算符 | 变量=表达式 | 右到左 | |
| /= | 除后赋值 | 变量/=表达式 | |||
| *= | 乘后赋值 | 变量*=表达式 | |||
| %= | 取模后赋值 | 变量%=表达式 | |||
| += | 加后赋值 | 变量+=表达式 | |||
| -= | 减后赋值 | 变量-=表达式 | |||
| <<= | 左移后赋值 | 变量<<=表达式 | |||
| >>= | 右移后赋值 | 变量>>=表达式 | |||
| &= | 按位与后赋值 | 变量&=表达式 | |||
| ^= | 按位异或后赋值 | 变量^=表达式 | |||
| |= | 按位或后赋值 | 变量|=表达式 | |||
| 15 | , | 逗号运算符 | 表达式,表达式,… | 左到右 |
双指针
双指针算法是一种通过设置两个指针不断进行单向移动来解决问题的算法。

例题:
给定一个长度为n的数组a和一个整数x,现在要请你在数组中寻找一个区间,使得这个区间的元素之和等于x。这样的区间存在多个,请按字典序大小输出。
CODE:
signed main(){
cin>>n;
for(int i=1;i<=n;i++) cin>>a[i];
cin>>m;
while(sum<m&&r<n) sum+=a[++r];
if(r==n) return 0;
if(sum==m) cout<<l<<' '<<r<<'\n';
for(r++;r<=n;r++){
sum+=a[r];
while(sum-a[l]>=m&&l<=r) sum-=a[l++];
if(sum==m) cout<<l<<' '<<r<<'\n';
}
return 0;
}
前缀和与差分
前缀和
一维:
对于数组 A[]
设置前缀和数组为 \(sum_i=\sum_{j=1}^i {A_j}\)
因此 A[l]+A[l+1]+···+A[r-1]+A[r] = sum[r]-sum[l-1]
二维:
对于数组:A[][]
设置前缀和数组为: \(sum_{i,j}=\sum_{u=1}^i \sum_{v=1}^j A_{u,v}\)
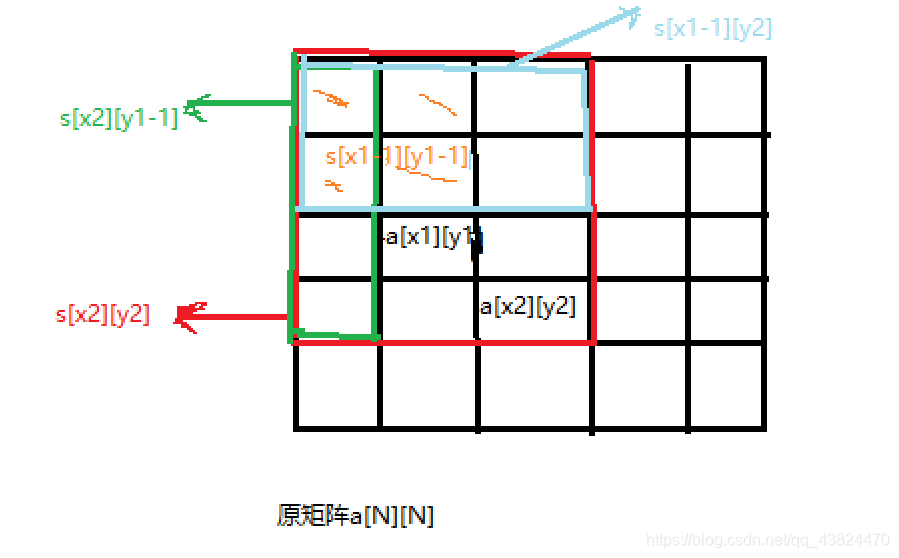
因此 \(\sum_{u=a}^b \sum_{v=c}^d A_{u,v} = sum_{b,d}-sum_{a,d}-sum_{b,c}+sum_{a,c}\)
图是:
适用场景
查询区间多,修改少。
差分
对于数组 A[]
设置差分数组为: d[i] = A[i]-A[i-1] (d[1]=A[1])
因此: A[i] = d[1]+d[2]+d[3]+···+d[i]
适用场景
修改多,查询少。
二分靠左
int ask_l(int k){
int r=1,l=n;
while(r<l){
int mid=(r+l)/2;
if(a[mid]>=k) l=mid;
else r=mid+1;
}
if(a[r]==k) return r-1;
return -1;
}
二分靠右
int ask_r(int k){
int r=1,l=n;
while(r<l){
int mid=(r+l+1)/2;
if(a[mid]>k) l=mid-1;
else r=mid;
}
if(a[r]==k) return r-1;
return -1;
}
二分查找相关函数 若存在序 a{0,1,3,3,3,5,8};
1. binary_search(a+1,a+n+1,x)
查找单调序列中,在指定区域内[1,n]是否存在目标值x。存在返回true,不存在返回false
例:int k=binary_search(a+1,a+7,3);//k=1
2. lower_bound(a+1,a+n+1,x)
查找不降序列中,在指定区域内[1,n]大于等于目标值x的第一个元素所在地址。(靠左查找)
例:int pos=lower_bound(a+1,a+7,3)-a;//元素位置在a+2,因此pos=2。
3. upper_bound(a+1,a+n+1,x)
查找不降序列中,在指定区域内[1,n]大于目标值x的第一个元素所在地址。(靠右查找)
例:int pos=lower_bound(a+1,a+7,3)-a;//元素位置在a+5,因此pos=5。
倍增
主要运用于:
LCA
void dfs(int x,int fa){
f[x][0]=fa;
dep[x]=dep[fa]+1;
for(int i=1;i<=20;i++)
f[x][i]=f[f[x][i-1]][i-1];
for(int i=head[x];i;i=nxt[i]){
int y=ver[i];
if(y==fa) continue;
dfs(y,x);
}
}
int lca(int a,int b){
if(dep[a]<dep[b]) swap(a,b);
for(int i=20;i>=0;i--){
if(dep[f[a][i]]>=dep[b])
a=f[a][i];
}
if(a==b) return a;
for(int i=20;i>=0;i--){
if(f[a][i]!=f[b][i])
a=f[a][i],b=f[b][i];
}
return f[a][0];
}
DP优化
请转到 DP动态规划。
排序
最实用的排序做法
sort: 升序排序
各大排序算法比较
| 排序算法 | 时间复杂度(最坏) | 时间复杂度(平均) | 时间复杂度(最好) | 空间复杂度 | 稳定性 | 核心特点与适用场景 |
|---|---|---|---|---|---|---|
| 冒泡排序 | O(n²) | O(n²) | O(n)(优化后) | O(1) | 稳定 | 简单直观,适合极小规模数据;优化后可提前终止,但效率低,实际应用少。 |
| 选择排序 | O(n²) | O(n²) | O(n²) | O(1) | 不稳定 | 简单,交换次数少,但无论数据是否有序都需遍历,适合数据量极小且交换成本高的场景。 |
| 插入排序 | O(n²) | O(n²) | O(n) | O(1) | 稳定 | 对部分有序数据效率高(如接近有序的数组),适合小规模数据或作为其他算法的子步骤(如桶排序)。 |
| 归并排序 | O(n log n) | O(n log n) | O(n log n) | O(n) | 稳定 | 效率稳定,适合大规模数据,可并行化,但需额外空间存储临时数组。 |
| 快速排序 | O(n²) | O(n log n) | O(n log n) | O(log n) | 不稳定 | 实际应用中平均速度最快,适合大规模数据,但最坏情况性能差(可通过随机基准优化)。 |
| 堆排序 | O(n log n) | O(n log n) | O(n log n) | O(1) | 不稳定 | 时间稳定且空间最优,适合大规模数据,但对缓存不友好(随机访问多),实际速度略慢于快排。 |
| 计数排序 | O(n + k) | O(n + k) | O(n + k) | O(n + k) | 稳定 | 非比较排序,适合数据范围小的整数(如0~1000),速度极快,但受限于数据范围。 |
| 桶排序 | O(n²) | O(n + k) | O(n + k) | O(n + k) | 稳定 | 依赖数据分布,适合均匀分布的大规模数据(如浮点数),桶内排序影响整体性能。 |
| 基数排序 | O(d*(n + k)) | O(d*(n + k)) | O(d*(n + k)) | O(n + k) | 稳定 | 按位排序,适合整数或固定长度字符串,无需比较大小,但位数d影响效率。 |
| std::sort | O(n log n) | O(n log n) | O(n log n) | O(log n) | 不稳定 | 标准库混合实现(快速排序+堆排序+插入排序),优化成熟,适合绝大多数场景。 |


 浙公网安备 33010602011771号
浙公网安备 33010602011771号