数学章节总结
总结不全,请各位 大佬 不要嘲讽。
质数筛选
Eratosthenes 筛法
从 2 开始,把它的倍数标记为合数,当搜索到某一个数但他未被标记过,说明他是质数。
代码:
bool v[1000000005];
int prime[1000005],tot;
void primes(int a){
for(int i=2;i<=a;i++){
if(v[i]) continue;
else prime[++tot]=i;
for(int j=i;j<=a/i;j++) v[i*j]=1;
}
}
时间复杂度:\(\mathcal O(N \log \log N)\), 因为 \(\log \log N\) 很小,所以近似于 \(\mathcal O(N)\)
线性筛
在 Eratosthenes 筛法的基础上进行优化:
我们发现,如 6= 2 * 3 或 3 * 2 会被标记两次 or 多次,所以我们可以规定只让那个数的最小质因子标记。
代码:
void primes(int a){
for(int i=2;i<=a;i++){
if(v[i]==0){
v[i]=i;prime[++tot]=i;
}
for(int j=1;j<=tot;j++){
if(prime[j]>v[i]||prime[j]>a/i) break;
v[i*prime[j]]=prime[j];
}
}
}
时间复杂度:\({\mathcal O(N)}\)
质因数分解
把从 \(1\) ~ \(n\) 的所有质数带进 \(n\) 中试一下,
就可以解决这个问题。
#include<bits/stdc++.h>
using namespace std;
/*!@#$%^&*!@#$%^&*~~优美的分界线~~*&^%$#@!*&^%$#@!*/
int T,n,tot,prime[40005],v[40005];
/*!@#$%^&*!@#$%^&*~~优美的分界线~~*&^%$#@!*&^%$#@!*/
void primes(int a){
for(int i=2;i<=a;i++){
if(v[i]==0) {
v[i]=i;prime[++tot]=i;
}
for(int j=1;j<=tot;j++){
if(prime[j]>v[i]||prime[j]>a/i) break;
v[i*prime[j]]=prime[j];
}
}
}
/*!@#$%^&*!@#$%^&*~~优美的分界线~~*&^%$#@!*&^%$#@!*/
signed main(){
cin>>n;
primes(n);
for(int i=1;i<=tot;i++){
int sum=0;
while(n%prime[i]==0&&n!=1){
sum+=1,n/=prime[i];
}
if(sum!=0) cout<<prime[i]<<' '<<sum<<'\n';
}
return 0;
}
时间复杂度: \(\mathcal O (N)\)
约数
性质:
- N 的正约数个数:
\((c_1+1)(c_2+1)(c_3+1) \times ··· \times (c_m+1)\)- N 的正约数之积:
\((1+p_1+p_1^2+···+p_1^{c_1}) \times ``` \times (1+p_m+p_m^2+···+p_m^{c_m})\)
筛法求约数个数
在用线性筛时,可以顺带求出 N 的约数集合。
\(a_{i}\) 表示 i 的最小质因子个数,\(ans_{i}\) 表示 i 的约数个数。
在线性筛中,如果合数 \(i\) 为小于它当前最小质因子的质数 \(p\) 的倍数时。\(i \times p\) 中 p 的个数为 \(a_{i}+1\), 根据性质 1,\(ans_{i \times prime[j]}=ans_{i}/(a_{i}+1) \times (a_{i \times prime[j]}+1);\)
否则,\(i \times p\) 中 \(p\) 的个数必然为 1, 根据推论 1,\(ans_{i \times prime[j]}=2 \times ans_{i};\)。
可得到:
if(i%prime[j]==0){
A[i*prime[j]]=A[i]+1;
B[i*prime[j]]=B[i]/(A[i]+1)*(A[i*prime[j]]+1);
break;
}else{
A[i*prime[j]]=1;
B[i*prime[j]]=B[i]*2;
}
完整代码:
#include<bits/stdc++.h>
using namespace std;
/*!@#$%^&*!@#$%^&*~~优美的分界线~~*&^%$#@!*&^%$#@!*/
int n,A[100000005],B[100000005];
int v[100000005];
int prime[100000005],tot;
/*!@#$%^&*!@#$%^&*~~优美的分界线~~*&^%$#@!*&^%$#@!*/
void primes(int a){
B[1]=1;
for(int i=2;i<=a;i++){
if(v[i]==0) {
v[i]=i;prime[++tot]=i;
B[i]=2;
A[i]=1;
}
for(int j=1;j<=tot;j++){
if(prime[j]>v[i]||prime[j]>a/i) break;
v[i*prime[j]]=prime[j];
if(i%prime[j]==0){
A[i*prime[j]]=A[i]+1;
B[i*prime[j]]=B[i]/(A[i]+1)*(A[i*prime[j]]+1);
break;
}else{
A[i*prime[j]]=1;
B[i*prime[j]]=B[i]*2;
}
}
}
}
/*!@#$%^&*!@#$%^&*~~优美的分界线~~*&^%$#@!*&^%$#@!*/
signed main(){
cin>>n;
primes(n);
for(int i=1;i<=n;i++){
cout<<B[i]<<'\n';
}
return 0;
}
最大公约数
性质:
- \(\gcd (ma,mb)\ =\ m \times \gcd (a,b)\)
- \(\gcd (a,b)+ \operatorname{lcm}(a,b)\ = \ a \times b\)
- 若 $d|a~~d|b \ $ 则 $ d| \gcd (a,b)$
- 若 $a|m~~b|m \ $ 则 $ \ \operatorname{lcm}(a,b)|m$
计算方法:
- 欧几里得算法(辗转相除法)
int gcd(int a, int b) {
if (a == 0) return b;
return gcd(b % a, a);
}
时间复杂度: \(\mathcal O (\log {N})\)
- 更相减损法(Stein算法) (奇偶性优化)
int gcd(int a,int b){
if(a==b) return a;
if(a%2==0 && b%2==0) return 2*gcd(a/2,b/2);
else if(a%2==0) return gcd(a/2,b);
else if(b%2==0) return gcd(a,b/2);
else return gcd(b,a-b);
}
时间复杂度: \(\mathcal O (\log {N})\)
欧拉函数
欧拉函数的定义
在数论中,对正整数 n,** 欧拉函数 φ(n)** 是小于或等于 n 的正整数中与 n 互质的数的数目。如:
φ(1)=1, φ(2)=1, φ(3)=2, φ(4)=2, φ(5)=4
计算欧拉函数
当把一个数分解成如下:
\(n=p_1^{c_1}p_2^{c_2}p_3^{c_3}···p_m^{c_m}\)
可得:
\(φ(n)=n \times \frac{p_1-1}{p_1} \times \frac{p_2-1}{p_2} \times ··· \times \frac{p_m-1}{p_m}=n \times (1-\frac{1}{p_1} ) \times (1-\frac{1}{p_2} ) \times ··· \times (1-\frac{1}{p_m} )\)
性质
- 若 \(a, b\) 互质,则 \(\varphi(a b)=\varphi(a) \varphi(b)\)。
- 设 \(p\) 为质数,若 \(p \mid n\) 且 \(p^{2} \mid n\),则 \(\varphi(n)=\varphi(n / p) \times p\)。
- 设 \(p\) 为质数,若 \(p \mid n\) 但 \(p^{2} \nmid n\),则 \(\varphi(n)=\varphi(n / p) \times (p-1)\)。
- \(φ(N)= {\textstyle \prod_{i=1}^{m}} φ(p_i^{c_i})\)
证明:
- 根据欧拉函数的计算式,对 \(a, b\) 分解质因数,直接可得性质 \(1\)。
- 若 \(p \mid n\) 且 \(p^{2} \mid n\),则 \(n, n / p\) 包含相同的质因子,只是 \(p\) 的指数不同。直接把 \(\varphi(n) 与 \varphi(n / p)\) 按照欧拉函数的计算公式写出,二者相除,商为 \(p\),所以性质 \(2\) 成立。
- 若 \(p \mid n\) 但 \(p^{2} \nmid n\),则 \(p\), \(n / p\) 互质,由 \(\varphi\) 是积性函数得 \(\varphi(n)=\varphi(n / p) \times \varphi(p)\),而 \(\varphi(p)=p-1\),所以性质 3 成立。
- 性质 3 易证
线性求欧拉函数:
void primes(int a){
for(int i=2;i<=a;i++){
if(v[i]==0) {
v[i]=i;prime[++tot]=i;
phi[i]=i-1;
}
for(int j=1;j<=tot;j++){
if(prime[j]>v[i]||prime[j]>a/i) break;
v[i*prime[j]]=prime[j];
if(i%prime[j]==0) phi[i*prime[j]]=prime[j]*phi[i];
else phi[i*prime[j]]=(prime[j]-1)*phi[i];
}
}
}
同余
定义
当两个整数 a,b 满足 a mod d = b mod d, 则 a≡b (mod d)
性质
- 反身性:\(a≡a (mod m)\);
- 对称性:若 \(a≡b\pmod{m}\),则 \(b≡a\pmod{m})\);
- 传递性:若 \(a≡b\pmod{m}\),\(b≡c\pmod{m}\),则 \(a≡c\pmod{m}\);
- 同余式相加:若 \(a≡b\pmod{m}\),\(c≡d\pmod{m}\),则 \(a+c≡b+d\pmod{m}\);
- 同余式相乘:若 \(a≡b\pmod{m}\),\(c≡d\pmod{m}\),则 \(a*c≡b*d\pmod{m}\)。
- 幂运算:如果 \(a≡b \pmod{m}\),那么 \(a^n≡b^n \pmod{m}\);
- \(\color{yellow} {注意!!!}\) 同余没有同除性,只有 \(a*c≡b*c\pmod{m}\),(在 \(\gcd(c,m)=1\) 时)。
欧拉定理
若 \(\gcd (a,m)=1\), 则 \(a^{φ(m)}≡1(mod\ m)\)
首先,我们要先了解一个简化剩余系:
简化剩余系 (reduced residue system) 也称既约剩余系或缩系,是 m 的完全剩余系中与 m 互素的数构成的子集,如果模 m 的一个剩余类里所有数都与 m 互素,就把它叫做与模 m 互素的剩余类。在与模 m 互素的全体剩余类中,从每一个类中各任取一个数作为代表组成的集合,叫做模 m 的一个简化剩余系。例如,模 5 的一个简化剩余系是 1,2,3,4,模 10 的一个简化剩余系是 1,3,7,9,模 18 的一个简化剩余系是 1,5,7,11,13,17。
还有几个引理:
-
引理 1 :
- 若 a,b,c 为任意 3 个整数,m 为正整数,且 m 与 c 互质,则当 a⋅c≡b⋅c (mod m) a⋅c ≡ b⋅c (mod m) 时,有 a ≡ b (mod m)
- 证明:a⋅c≡b⋅c (mod m) 可得 ac−bc≡0 (mod m),即 (a−b)⋅c≡0 (mod m) 。因为 mm 与 cc 互质,所以 cc 不可能为 mm 的倍数,即 a−b≡0 (mod m) ,所以 a≡b (mod m) 。
证毕。
-
引理 2:
- 若 a,b 属于 mm 的简化剩余系,那么 a×b 仍属于 m 的简化剩余系(即 m 的简化剩余系关于模 m 乘法封闭)。
- 证明:若 a,b 与 m 互质,即 a,b 不含有与 m 相同的质因子,那么 a×b 也不可能与 m 含有相同的质因子,即 a×b 也与 m 互质,所以 a×b 仍属于 m 的简化剩余系。
证毕。
-
引理 3 :
- 若 n 与 m 互质,且 { \({ \bar{a_1},\bar{a_2},bar{a_3},⋯,\bar{a_m}}\)} 为 m 的完全剩余系,则 { \({ n\bar{a_1},n\bar{a_2},n\bar{a_3},⋯,n\bar{a_m}}\)} 也构成 m 的完全剩余系。
- 证明:若存在 \(na_i 与 na_j\) 同余即 \(na_i≡na_j(modm)\),由引理 1 可得 \(a_i≡aj(modm)\),与条件不符,故假设不成立。
证毕。
-
引理 4 :
- 若 n 与 m 互质,且 { \({ \bar{a_1},\bar{a_2},\bar{a_3},⋯,\bar{a_{φ(n)}}}\)} 为 m 的简化剩余系,则 { \({ n\bar{a_1},n\bar{a_2},n\bar{a_3},⋯,n\bar{a_{φ(n)}}}\)} 也构成 m 的简化剩余系。
- 证明:由引理 2 以及引理 3 易证。
证毕。
证明:
-
构造 n 的简化剩余系为
{ \({ \bar{a_1},\bar{a_2},\bar{a_3},⋯,\bar{a_{φ(n)}}}\)}
-
那么根据引理 4 得:
\(a_1a_2a_3···a_{φ(n)}≡aa_1 \times aa_2··· \times aa_m≡a^{φ(n)} \times a_1a_2a_3···a_{φ(n)}\)
-
根据简化剩余系的定义可知 \(a_{φ(n)}≡1(mod\ n)\)
证毕。
也可得:
\(A^B≡A^{B\ mod\ φ(n)}(mod\ n)\)
欧拉定理的一点点小扩展
费马小定理
若 p 是质数,则对于任意满足不是 p 的倍数的 a,有 \(a^{p−1}≡1~~(mod\ p)\)
这个定理的主要作用是求出逆元。
证明:
当p是质数,\(\phi(p)=p-1\),所以将其带入欧拉定理,
扩展欧几里得定理
用处: 求出 (ax + by = c) 的整数解
有解: 当 c 为 gcd (a,b) 时
解法: 设当前为 a1,b1; 下一次为 b,a% b;
所以:
- 当 b1==0, 则 a1 * x+0 * y=gcd (a,0), 则 x = 1,y = 1;
- 当 b1==0 则 b * x+(a% b)*y = a*y + b*(x-a/b * y)=gcd (b,a% b)=gcd (a,b)。
代码:
void gcd(int a, int b,int &n,int &m) {
if (b == 0) {
n=1,m=0;
return ;
}
int x1,y1,d;
gcd(b,a%b,x1,y1);
n=y1,m=x1-a/b*y1;
return ;
}
逆元
什么是逆元:
a * x ≡ 1 (mod p) 其中 x 叫做 a 的关于 p 的逆元,记为:inv (a) = x
所以 a * inv (a) ≡ 1 (mod p)
如何求 a 在 mod m 下的逆元:
因为 a*x ≡ 1 (mod \ p), 所以可得:a*x-p*y = 1(y 为 整数)。
这像什么:a * x+b * y=c (x,y 为整数),于是我们可以用扩展欧几里得定理解决这个问题
逆元有什么用:
首先,当我们计算类似 \((a / b) \mod p\) 的时候,我们很容易计算成 \((a / b) \mod p = (a\modp/ b\modp) \mod p\), 但是其实这是错误的。
比如:(100/50)%20 = 2 ≠ (100%20) / (50%20) %20 = 0
但是有一些题,数字太大,必须先算 % 号。又因为 \(a \times b\%c=a\%c \times b\%c\), 所以需要把 / 变成 *。
你可能会认为这不简单!,小学生都知道 \(/a= \times 1/a\),
但在数论中并不是这样,这个乘数就是逆元。
一句话就是,将除法改为乘法
中国剩余定理
1. 中国剩余定理(曹冲养猪)
题目描述:
给定 n 组非负整数 \(a_i\), \(b_i\),求解关于 \(x\) 的方程组的最小非负整数解。
\(\begin{cases} x≡r_1\ (mod\ m_1) \\ x≡r_2\ (mod\ m_2) \\ ···\\ x≡r_n\ (mod\ m_n) \\ \end{cases}\)
你可以假定 \(m_1∼m_n\) 互质。
做法:
- 设 \(M\) 为所有 \(m\) 的乘积。
- 设 \(C_i\) 为 \(M/m_i\)。
- 求每一个 \(C_i\) 的逆元:\(C_i^{-1}\)
- \(ans=\displaystyle\sum_{i=1}^n r_i \times C_i \times C_i^{-1}\)
证明:
取出前两个同余式:
\(\begin{cases} a≡r_1\ (mod\ m_1) \\ a≡r_2\ (mod\ m_2) \end{cases}\)
可以得到:
\(\begin{cases} a=r_1+m_1 \times x \\ a=r_2+m_2 \times y \end{cases}\)
得到:
\(r_1+m_1 \times x=r_2+m_2 \times y\)
\(m_1 \times x-m_2 \times y=r_2-r_1\)
因此,可以解出 x,y 的一组特解 \(x_0,y_0\)。因而通解为 \(X=x_0+m_2/ \gcd (m_1,m_2) \times k\) (k 为任意整数)
则:a 的通解为 \(r_1+m_1 \times x_0+m_1 \times m_2/ \gcd (m_1,m_2) \times k\)
可以写为 \(a≡(r_1+m_1 \times x)\ (mod\ m_1 \times m_2/ \gcd (m_1,m_2))\)
因此我们能够把两个同余式合为一个同余式
2. 扩展中国剩余定理
题目描述:
给定 n 组非负整数 \(a_i\), \(b_i\),求解关于 \(x\) 的方程组的最小非负整数解。
\(\begin{cases} x≡r_1\ (mod\ m_1) \\ x≡r_2\ (mod\ m_2) \\ ···\\ x≡r_n\ (mod\ m_n) \\ \end{cases}\)
算法:
#include<bits/stdc++.h>
#define int __int128
using namespace std;
/*!@#$%^&*!@#$%^&*~~优美的分界线~~*&^%$#@!*&^%$#@!*/
int n;
int l[100005][3];
/*!@#$%^&*!@#$%^&*~~优美的分界线~~*&^%$#@!*&^%$#@!*/
int exgcd(int a, int b,int &n,int &m) {
if (b == 0) {
n=1,m=0;
return a;
}
int x1,y1,d;
d=exgcd(b,a%b,x1,y1);
n=y1,m=x1-a/b*y1;
return d;
}
inline int read(){
int ans=0,j=1;char c=getchar();
while(c>'9' or c<'0'){if(c=='-')j=-1;c=getchar();}
while(c>='0' and c<='9'){ans=ans*10+c-'0';c=getchar();}
return ans*j;
}
inline void write(int x){
if(x<0){putchar('-');x=-x;}
if(!x)return;write(x/10);putchar(x%10+'0');
}
/*!@#$%^&*!@#$%^&*~~优美的分界线~~*&^%$#@!*&^%$#@!*/
signed main(){
n=read();
for(int i=1;i<=n;i++) l[i][1]=read(),l[i][2]=read();
int R=l[1][1],M=l[1][2];
for(int i=2;i<=n;i++){
int r1=R,r2=l[i][1],m1=M,m2=l[i][2];
int x0,y0,G=exgcd(m1,m2,x0,y0);
if((r2-r1)%G!=0) {
return 0;
}
x0=x0*(r2-r1)/G;
x0=(x0%m2+m2)%m2;
M = (m1*m2)/G,R = m1*x0+r1;
}
R=(R%M+M)%M;
write(R);
return 0;
}
//153456180035
矩阵乘法与高斯消元
矩阵乘法
定义:
乘积矩阵第 i 行第 j 列处的元素等于左矩阵的第 i 行与右矩阵的第 j 列对应元素乘积之和模板:
struct matrix{
int a[3][3];
matrix(){
memset(a,0,sizeof a);
}
void print(){
for(int i=1;i<=n;i++){
for(int j=1;j<=n;j++) cout<<a[i][j]<<' ';
cout<<'\n';
}
}
};
matrix operator *(matrix a,matrix b){
matrix c;
for(int i=1;i<=2;i++)
for(int j=1;j<=2;j++)
for(int x=1;x<=2;x++)
c.a[i][j]=(c.a[i][j]+a.a[i][x]*b.a[x][j])%Mod;
return c;
}
矩阵加速
使用矩阵加快计算速度,如:
\(在斐波那契数列中,Fib_0=0,Fib_1=1,Fib_n=Fib_{n-2}+Fib_{n-2}。给定整数 n,求 Fib_n~mod~10000\)
做法:
我们可以构造一个矩阵为:
A=\(\begin{bmatrix} 1 & 1 \\ 1 & 0 \end{bmatrix}\)
和
B =\(\begin{bmatrix} x \\ x \end{bmatrix}\)
第一个是转移矩阵,第二个为答案矩阵
我们能得到:
\(B[i]=A*B[i-1]\)
展开后:
\(B [n]=A^{n-2}*\begin{bmatrix}1 \\1\end{bmatrix}\)
因此,我们能用 KSM 快速幂优化 A^(n-2) 的部分,减少时间 \(\mathcal O (\log n)\).
代码:
#include<bits/stdc++.h>
#define int long long
using namespace std;
/*!@#$%^&*!@#$%^&*~~优美的分界线~~*&^%$#@!*&^%$#@!*/
const int Mod=1e4;
int n;
struct matrix{
int a[3][3];
matrix(){
memset(a,0,sizeof a);
}
void print(){
for(int i=1;i<=n;i++){
for(int j=1;j<=n;j++) cout<<a[i][j]<<' ';
cout<<'\n';
}
}
};
/*!@#$%^&*!@#$%^&*~~优美的分界线~~*&^%$#@!*&^%$#@!*/
matrix operator *(matrix a,matrix b){
matrix c;
for(int i=1;i<=2;i++)
for(int j=1;j<=2;j++)
for(int x=1;x<=2;x++)
c.a[i][j]=(c.a[i][j]+a.a[i][x]*b.a[x][j])%Mod;
return c;
}
matrix pow(matrix a,int k){
matrix ans;
for(int i=1;i<=2;i++) ans.a[i][i]=1;
while(k) {
if(k&1) ans=ans*a;
a=a*a;k>>=1;
}
return ans;
}
/*!@#$%^&*!@#$%^&*~~优美的分界线~~*&^%$#@!*&^%$#@!*/
signed main(){
while(cin>>n&&n!=-1){
if(n==0||n==1){
cout<<n<<'\n';
continue;
}
matrix A;
A.a[1][1]=A.a[1][2]=A.a[2][1]=1;
A=pow(A,n-2);
cout<<(A.a[1][1]+A.a[1][2])%Mod<<'\n';
}
return 0;
}
高斯消元法:
- 高斯消元法:
bool geuss(){
for(int i=1;i<=n;i++){
for(int k=i;k<=n;k++)
if(fabs(l[k][i])>eps) {
swap(l[i],l[k]);
break;
}
if(fabs(l[i][i])<eps) return 0;
for(int j=n+1;j>=i;j--) l[i][j]/=l[i][i];
for(int j=i+1;j<=n;j++)
for(int k=n+1;k>=i;k--)
l[j][k]-=l[i][k]*l[j][i];
}
for(int i=n-1;i>=1;i--)
for(int j=i+1;j<=n;j++)
l[i][n+1]-=l[i][j]*l[j][n+1];
return 1;
}
- 约旦消元法:
bool geuss(){
for(int i=1;i<=n;i++){
for(int k=i;k<=n;k++)
if(fabs(l[k][i])>eps) {
swap(l[i],l[k]);
break;
}
if(fabs(l[i][i])<eps) return 0;
for(int k=1;k<=n;k++){
if(k==i) continue;
double p=l[k][i]/l[i][i];
for(int j=i;j<=n+1;j++)
l[k][j]-=l[i][j]*p;
}
}
return 1;
}
- 矩阵求逆:
#include<bits/stdc++.h>
#define int long long
using namespace std;
/*!@#$%^&*!@#$%^&*~~优美的分界线~~*&^%$#@!*&^%$#@!*/
const int Mod=1e9+7;
int n;
int l[405][805];
/*!@#$%^&*!@#$%^&*~~优美的分界线~~*&^%$#@!*&^%$#@!*/
int ksm(int x,int y){
int ans=1;
while(y){
if(y&1) ans*=x,ans%=Mod;
x=(x*x)%Mod,y>>=1;
}
return ans%Mod;
}
bool geuss(){
for(int i=1;i<=n;i++){
for(int k=i;k<=n;k++)
if(abs(l[k][i])!=0) {
swap(l[i],l[k]);
break;
}
if(abs(l[i][i])==0) return 0;
int ny=ksm(l[i][i],Mod-2);
for(int k=1;k<=n;k++){
if(k==i) continue;
int p=(l[k][i]*ny)%Mod;
for(int j=i;j<=2*n;j++)
l[k][j]-=l[i][j]*p,l[k][j]=(l[k][j]%Mod+Mod)%Mod;
}
for(int k=i;k<=n*2;k++) l[i][k]=(l[i][k]*ny)%Mod;
}
return 1;
}
/*!@#$%^&*!@#$%^&*~~优美的分界线~~*&^%$#@!*&^%$#@!*/
signed main(){
cin>>n;
for(int i=1;i<=n;i++){
l[i][i+n]=1;
for(int j=1;j<=n;j++)
cin>>l[i][j];
}
if(geuss()){
for(int i=1;i<=n;i++){
for(int j=1;j<=n;j++)
cout<<l[i][j+n]<<' ';
puts("");
}
}else cout<<"No Solution";
return 0;
}
组合技数
求 c(n,m):
公式 + 快速幂:
int ksm(int x,int y){
int ans=1;
while(y){
if(y&1) ans*=x,ans%=Mod;
x=(x*x)%Mod,y>>=1;
}
return ans%Mod;
}
int jc(int x){
int ans=1;
for(int i=1;i<=x;i++) ans*=i,ans%=Mod;
return ans;
}
int f1(){
int a1=jc(k);
int a2=jc(n)*jc(k-n)%Mod;
a2=ksm(a2,Mod-2);
return a1*a2%Mod;
}
优化:
int ksm(int x,int y){
int ans=1;
while(y){
if(y&1) ans*=x,ans%=P;
x=(x*x)%P,y>>=1;
}
return ans%P;
}
int f(int n,int m){
int ma=1,mb=1;
for(int i=1;i<=m;i++) mb=(mb*i)%P;
for(int i=n-m+1;i<=n;i++) ma=(ma*i)%P;
return ma*ksm(mb,P-2)%P;
}
/*
这种适用于n很大,m很小的情况,时间复杂度:O(m+log P)
*/
递推:
for(int i=1;i<=x;i++){
for(int j=1;j<=k;j++){
c[i][j]=c[i-1][j]+c[i-1][j-1];
}
}
基本公式
基本定义 \(C(n, m) = \frac{n!}{m!(n-m)!}\)
对称性
\(C(n, m) = C(n, n-m)\)
递推公式(帕斯卡恒等式)
\(C(n, m) = C(n-1, m-1)+C(n-1, m)\)
特殊值公式
\((C(n, 0) = C(n, n) = 1 .)\)
阶乘化简形式
\(C(n, m) = \frac{n \cdot(n-1) \cdot(n-2) \cdots(n-m+1)}{m!}\)
所有组合数之和
\(\sum_{m = 0}^{n} C(n, m) = 2^{n}\)
奇数项与偶数项的和
\(\sum_{m \text { 为奇数 }} C(n, m) = \sum_{m \text { 为偶数 }} C(n, m) = 2^{n-1} \text {. }\)
组合数与排列数的关系
\(C(n, m) = \frac{P(n, m)}{m!}, \quad P(n, m) = \frac{n!}{(n-m)!}\)
平方和公式
\(\sum_{m = 0}^{n}[C(n, m)]^{2} = C(2 n, n)\)
二项式定理的定义
二项式定理表明,对于任何非负整数 n ,一个二项式 (a + b) 的 n 次幕的展开形式可以表示为:
\((a+b)^{n}=\sum_{k=0}^{n} C(n, k) \cdot a^{n-k} \cdot b^{k}\)
容斥与莫比乌斯函数及概率期望
容斥:
引入:
这里有三个集合:A B C ,如果我们要求其并集的大小:
\(|𝐴∪𝐵∪𝐶|=|𝐴|+|𝐵|+|𝐶|−|𝐴∩𝐵|−|𝐵∩𝐶|−|𝐶∩𝐴|+|𝐴∩𝐵∩𝐶|\)
解释如图:
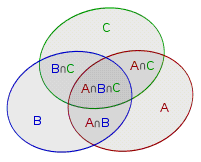
进一步推广,便可以得到容斥原理。
例题:
小明最近在学习组合数学,他对于“染色问题”产生了浓厚的兴趣。某天,他收到一项任务,要求他为一批球进行染色。这些球需要用特定数量的颜色进行染色,同时还需要满足所有颜色必须至少使用一次的约束。小明思考了一会儿,觉得这似乎是一个有趣但又有挑战性的数学问题。他决定请聪明的你帮他解决。
现有 n 个球 和 m 种颜色。每种球可以被染成任意一种颜色,但要求 每种颜色至少染一个球。请你计算满足条件的不同染色方案数。
代码:
#include<bits/stdc++.h>
#define int long long
using namespace std;
/*!@#$%^&*!@#$%^&*~~优美的分界线~~*&^%$#@!*&^%$#@!*/
const int N=1e6+5,Mod=1e9+7;
int n,m,f[N],ans;
/*!@#$%^&*!@#$%^&*~~优美的分界线~~*&^%$#@!*&^%$#@!*/
int ksm(int x,int y){
int ans=1;
while(y){
if(y&1) ans*=x,ans%=Mod;
x=(x*x)%Mod,y>>=1;
}
return ans;
}
void init(){//阶乘
f[0]=1;
for(int i=1;i<N;i++) f[i]=f[i-1]*i%Mod;
}
int c(int n,int m){组合
return f[n]*ksm(f[m],Mod-2)%Mod*ksm(f[n-m],Mod-2)%Mod;
}
/*!@#$%^&*!@#$%^&*~~优美的分界线~~*&^%$#@!*&^%$#@!*/
signed main(){
init();
cin>>n>>m;
ans=0;
for(int i=0;i<=m;i++){
int idx=(i&1)?-1:1;//一加一减
int idx2 = ksm(m-i,n)*c(m,i)%Mod;//贡献
ans=((ans+idx*idx2)%Mod+Mod)%Mod;
}
cout<<ans;
return 0;
}
mobius 莫比乌斯函数:
定义:
\(\mu(n)=\left\{\begin{array}{ll} 1 & \text { 若 } n=1 ; \\ (-1)^{k} & \text { 若 } n \text { 无平方数因数, 且 } n=p_{1} p_{2} \ldots \ldots p_{k} ; ~ \\ 0 & \text { 若 } n \text { 有大于 } 1 \text { 的平方数因数。 } \end{array}\right.\)
求法:
在埃式筛基础上再加一点:
mo[1]=1;
for(int i=2;i<N;i++){
if(!v[i]){
prime[++cnt]=i;
mo[i]=-1;
}
for(int j=1;j<=cnt&&i*prime[j]<N;j++){
v[i*prime[j]]=1;
if(i%prime[j]==0) break;
mo[i*prime[j]]=mo[i]*-1;
}
}
01 分数规划与博弈论
这一章以Nim游戏为举例:
共有 \(𝑛\) 堆石子,第 \(𝑖\) 堆有 \(𝑎_𝑖\)枚石子。两名玩家轮流取走任意一堆中的任意多枚石子,但不能不取。取走最后一枚石子的玩家获胜。
在这样的游戏中,游戏的进行可以用有向图表示,如图(初始状态 1,1,2 )
其中红色为必胜态,黑色为必败态:
这里我们能够发现:
- 对于必胜态:只要他能到达的状态至少有一个必败态即可。
- 对于必败态:需要他能到达的状态全是必胜态。
Nim游戏:
结论:
只有所有石子数量异或和等于0,才后手必胜。



 浙公网安备 33010602011771号
浙公网安备 33010602011771号