CF1446E Long Recovery

令 \(P\) 为不同颜色相邻格子的数量，考虑更改一个格子 \(c\) 的颜色后会发生什么。

若与 \(c\) 相邻的格子均为不同颜色，则 \(P\) 将减去 \(3\)，否则 \(P\) 将减去 \(1\)。

显然我们需要让一操作的次数尽量少。

然后来考虑怎么判断无解：

根据第二个样例，如果某个时刻存在黑色格子的环，显然此时无解。否则，就有可能让一些黑色格子变白。假设 \(A\) 为初始的黑色格子点集，\(\overline{A}\) 为尽量染黑操作后形成的点集，显然当 \(\overline{A}\) 中包含这样一个环时无解，而 \(\overline{A}\) 可以直接通过 BFS 求出。

接下来认为 \(\overline {A}\) 中不存在环，且仅包含一个连通块（如果有多个分别考虑即可，记连通块数量为 \(D\)）。

首先可以发现最后一步必须要使用一操作，且只有当不能使用二操作时才会使用一操作。具体的，只有当 \(A\) 长成这个样子(称这个为 triforce)才需要一操作，且并不会出现其他情况，记 triforce 的数量为 \(Q\)。

证明：

假设 \(A\) 是一个至少有两个格子的集合，满足：

1. \(\overline{A}\) 中不存在环。

2. \(\overline{A}\) 连通。

3. \(A\) 不是 triforce。

可以发现存在一个二操作，满足操作后的集合 \(A'\) 仍然满足上面的条件，首先 1. 将一直满足，因为 \(\overline{A'}⊆\overline{A}\)。因此只需要证明后两个，即 \(A'\) 连通，且 \(A'\) 不是 triforce。

考虑分类讨论：

1. 存在一个二操作的白变黑，那么直接做就行，显然仍然满足上述条件。

2. 不存在二操作的白变黑，但是存在二操作让格子 \(c\) 黑变白，考虑操作后会发生什么：因为不存在二操作的白变黑，所以对于任何格子在 \(\overline{A}\backslash A\) 必定在 \(A\) 中有三个邻居。

因此至少两个在 \(A\backslash c\) 中，于是 \(\overline{A}\backslash A\subseteq \overline{A\backslash c}\)，即 \(\overline{A}\backslash c\backslash (A\backslash c)\subseteq \overline{A\backslash c}\)，又因为 \(A\backslash c\subseteq \overline{A\backslash c}\)，所以 \(\overline{A}\backslash c\subseteq \overline{A\backslash c}\)。

可以发现 \(\overline{A\backslash c}\) 一定连通，仍然分类讨论：

1. \(c\) 是 \(\overline{A}\) 的叶子，去掉后仍然连通。

2. \(c\) 不是 \(\overline {A}\) 的叶子，那么 \(c\) 至少有两个邻居在 \(\overline{A}\backslash c\) 中，即 \(\overline{A\backslash c}\) 中，所以 \(\overline{A\backslash c}=\overline A\)。

并且 \(A\backslash c\) 不是 triforce。假设 \(A\backslash c\) 是 triforce，那么 \(A\) 一定是 triforce 加上一个额外的格子，那么可以选择另一个满足条件的 \(c\)。

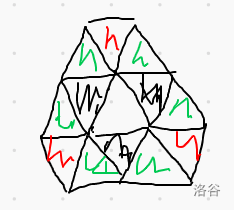
3. 不存在任何二操作，此时 \(A\) 中的格子互不相邻（因为相邻就是存在一棵大小 \(> 1\) 的树，那么一定存在一个叶子节点），并且 \(\overline{A}\backslash A\) 被 \(A\) 包围。且由于 \(A\) 至少有两个格子，且 \(\overline A\) 中不存在环，所以必须构造出 triforce 来满足条件。

如图，绿色格子因为在 \(A\) 中没有格子是相邻的所以不在 \(A\) 中，而红色格子因为 \(\overline A\) 会成环所以也不在 \(A\) 中。

因此 \(A\) 不能有除了这三个格子以外的格子，因为 \(\overline A\) 是连通的。

最后分别计算出 \(P,D,Q\)，答案就是 \(P-2\times D-2\times Q\)。

#include<bits/stdc++.h>
#define R(i,a,b) for(int i=(a),i##E=(b);i<=i##E;i++)
#define L(i,a,b) for(int i=(b),i##E=(a);i>=i##E;i--)
using namespace std;
int n;
int vis[255555],a[255555],b[255555];
vector<int>e[255555];
deque<int>q;
int ans;
int ok=1,cb,tr;
inline int gkd(int x,int y)
{
	return 501*x+y;
}
void dfs1(int u)
{
	if(vis[u]) return;
	vis[u]=1;
	for(int v:e[u]) if(a[v]) dfs1(v);
}
void dfs2(int u,int f)
{
	if(vis[u]==2)
	{
		ok=0;
		return;
	}
	vis[u]=2;
	if(a[u]) ++cb;
	for(int v:e[u]) if(v^f&&b[v]) dfs2(v,u);
	if(!a[u])
	{
		int cnt=0;
		for(int v:e[u]) cnt+=(a[v]==1);
		if(cnt==3) tr=1;
	}
}
signed main()
{
	ios::sync_with_stdio(false);
	cin.tie(NULL);
	R(i,1,500) R(j,1,500)
	{
		int u=gkd(i,j),v=gkd(i-1,j);
		e[u].emplace_back(v);
		v=gkd(i+1,j);
		e[u].emplace_back(v);
		if(i&1) v=gkd(i+1,j-1);
		else v=gkd(i-1,j+1);
		e[u].emplace_back(v);
	}
	cin>>n;
	R(i,1,n)
	{
		int u,v;
		cin>>u>>v;
		++u,++v;
		int x=gkd(u,v);
		a[x]=b[x]=1;
		q.emplace_back(x);
	}
	int ans1=0,ans2=0,ans3=0,u;
	R(i,1,500) R(j,1,500)
	{
		u=gkd(i,j);
		if(!vis[u]&&a[u]==1) dfs1(u),++ans1;
	} 
	while(q.size())
	{
		int u=q.front();q.pop_front();
		for(int v:e[u]) if(!b[v])
		{
			int cnt=0;
			for(int vv:e[v]) cnt+=(b[vv]==1);
			if(cnt>=2) b[v]=1,q.emplace_back(v);
		}
	}
	R(i,1,500) R(j,1,500) 
	{
		u=gkd(i,j);
		if(vis[u]!=2&&b[u]==1)
		{
			tr=cb=0;
			dfs2(u,u);
			++ans2;
			if(tr&&cb==3) ++ans3;
		}
	}
	if(!ok)
	{
		cout<<"SICK"<<'\n';
	}
	else 
	{
		cout<<"RECOVERED"<<'\n'<<n+2*(ans1-ans2-ans3)<<'\n';
	}
}