Accurate and Efficient Self-Localization on Roads using Basic Geometric Primitives

一、前言

这篇论文出自ICRA 2019，主要介绍如何通过环境中基本不变的三维几何特征实现自动驾驶汽车的实时定位。按照论文在摘要中的描述，该方案的定位精度能够小于10cm，定位频率可以达到50HZ。
在阅读该论文之前，建议阅读如下几篇文章：

1. Himmelsbach M, Hundelshausen F V, Wuensche H J. Fast segmentation of 3D point clouds for ground vehicles[C], 2010 IEEE Intelligent Vehicles Symposium. IEEE, 2010: 560-565.
2. Sefati M, Daum M, Sondermann B, et al. Improving vehicle localization using semantic and pole-like landmarks[C], 2017 IEEE Intelligent Vehicles Symposium (IV). IEEE, 2017: 13-19.
3. Poggenhans F, Schreiber M, Stiller C. A universal approach to detect and classify road surface markings[C], 2015 IEEE 18th International Conference on Intelligent Transportation Systems. IEEE, 2015: 1915-1921.

二、定位方案框架介绍

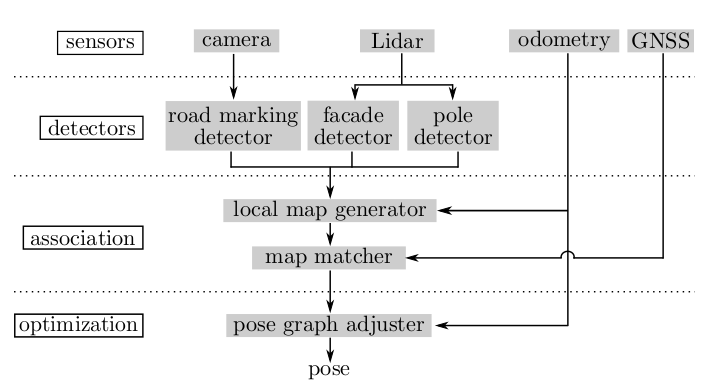
论文定位框架如下图所示，主要有四层: 传感器层、检测层、关联层和优化层。在传感器层中，主要包含相机、激光雷达、里程计和GNSS，相机主要用于路面标线的检测，而激光雷达则是用于提取环境中的立面和杆特征，里程计则作用是累滑动地图和优化位姿，GNSS则会为地图关联提供初始位姿。

三、特征提取方法

用于定位的特征主要有三类: 杆特征、面特征和路面标线，之所以选择这三类是因为它们在城市道路环境中相对稳定、能够保持长时间不变，因而可以提高算法的鲁棒性。下面将分别对这三类特征进行阐述。

杆特征

杆特征主要存在于交通标志牌、信号灯、路灯和树木等杆状物体中，论文中并没有详细说明如何提取这类特征，只是简单说明与《Improving vehicle localization using semantic and pole-like landmarks》所采用的方案类似。简单来说，杆特征的提取方法主要有三步：
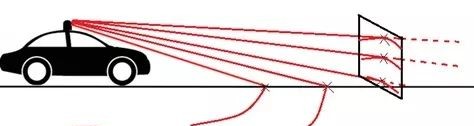
第一步(地面点删除)：按照《Fast segmentation of 3D point clouds for ground vehicles》所提出的基于极坐标栅格的斜率分类的方式来提取点云中的地面。该方法的思想如下图所示，也即同一时刻扫描到的地面点在斜率上应保持一致。

**第二步(聚类分割)：**将剩余的点云投影至2D占用栅格中，并保存每一栅格对应的最大高度。然后，对高度大于20cm的栅格进行聚类，并将聚类后高度过低且栅格较少的类融合到附件的类中，实现点云分割。 **第三步(杆提取)：**杆状物提取的方式则是先对点云进行层级划分(直接按照激光雷达的线束)，然后对每个层级进行圆拟合，比较每个点与拟合参数，选出符合杆特征的类，如下图所示： 最后是杆特征在地图中保存方式：该论文中并不是将提取出的点云直接使用，而是只存储了每个杆状物与地面的交点、以及它们的半径和倾角。这样的存储方式可以使得地图所占用的内存大幅减少。

面特征

面特征主要指的是建筑物的墙面，这写特征一般很少发生变化。至于如何提取点云中的面特征，论文没有进行任何说明，想来应该使用得是最简单的平面提取方法。而对于该特征在地图中保存的方式则是只保留平面与地面的交线，也即一个2D的线段。

路面标线

地面标线是视觉定位中经常使用的特征，而该论文采用的是《A Universal Approach to Detect and Classify Road Surface Markings》所提出的算法来提取相机采集到的路面标线，算法流程如下图所示，而由于涉及图像处理方面的内容，我不是很懂，留个坑，以后有机会再填。

至于地面标线在地图中的保存方式，则是两个2D点，它们描述标线长轴方向上的中心线。

四、特征关联

这一节主要介绍算法框架中的关联层，该层主要包含两部分：局部地图的建立和特征关联优化方法。

局部地图的建立

针对定位过程中局部地图可能存在的问题，作者提出了相应的解决方案：
问题一：在前一步中提取的几何特征无法像视觉特征那样有相应的描述子，这会给匹配造成一定的困难。
解决方法：结合多个特征，将它们相对位置记录为pattern，这些个pattern往往是独立存在于地图上的，因此关联问题将会被解决。
问题二：单帧点云或者单帧图像所测量的信息相对较少。
解决方法：截取一定时间和距离范围内的多帧数据，也即是滑动地图。具体截取的时间范围由如下公式决定：

\[ t_b = \begin{cases} t_e - \Theta_{t,max}, & \text{if $d(t_e - \Theta_{t,max},t_e)$ <$\Theta_{d,max}$} \\ t_d, & \text{else} \end{cases} \]

特征关联

为将局部地图\({\cal M_l}\)与全局地图\({\cal M_g}\)中的特征进行匹配关联，需要优化如下目标函数：

\[{\cal C}({\cal M_l}, {\cal M_g}, {\mathrm p})= \sum_{{\mathrm f_d} \in {\cal M_l}}{\cal C_f}({\mathrm f_d}, {\cal M_g}, {\mathrm p}) \]

其中，\({\mathrm p}\)为汽车位姿，\({\mathrm f_d}\)表示局部地图\({\cal M_l}\)中检测到的特征，而\({\cal C_f}({\mathrm f_d}, {\cal M_g}, {\mathrm p})\)的表达式如下：

\[{\cal C_f}({\mathrm f_d}, {\cal M_g}, {\mathrm p}) = \begin{cases} {\cal C_p}({\mathrm f_d}, {\cal M_g}, {\mathrm p}), & \text{if pole}\\ \omega_{f,1}{\cal C_s}({\mathrm f_d}, {\cal M_g}, {\mathrm p}) & \text{if facade}\\ \omega_{f,2}{\cal C_s}({\mathrm f_d}, {\cal M_g}, {\mathrm p}) & \text{if road marking} \end{cases} \]

对于杆状特征，它的优化关联方程\({\cal C_p}({\mathrm f_d}, {\cal M_g}, {\mathrm p})\)表达式如下：

\[{\cal C_p}({\mathrm f_d}, {\cal M_g}, {\mathrm p}) = \begin{cases} \frac{d_p({\mathrm f_d}, {\mathrm f_m}, {\mathrm p})}{d_{p,max}}+\omega_p\frac{\triangle\alpha({\mathrm f_d},{\mathrm f_m}, {\mathrm p})}{\triangle\alpha_{p,max}} & \text{if $\exists {\mathrm f_m}$} \\ 1+\omega_p & \text{else} \end{cases} \]

那么，从上式中可以看出，当能够在\({\cal M_g}\)中找到关联杆转特征\({\mathrm f_m}\)时，优化目标有两部分组成：距离偏差和倾角偏差。
对于面特征和路面标线，它们的优化关联方程相类似，可以统一表达为：

\[{\cal C_s}({\mathrm f_d}, {\cal M_g}, {\mathrm p})= \begin{cases} \frac{d_s({\mathrm f_d}, {\mathrm f_m}, {\mathrm p})}{d_{s,max}} + \omega_{s,1}\frac{\triangle\alpha_s({\mathrm f_d}, {\mathrm f_m}, {\mathrm p})}{\triangle\alpha_{s,max}} + \omega_{s,2}\frac{o_{out}({\mathrm f_d}, {\mathrm f_m}, {\mathrm p})}{o_{in}({\mathrm f_d}, {\mathrm f_m}, {\mathrm p})+o_{out}({\mathrm f_d}, {\mathrm f_m},{\mathrm p})} & \text{if $\exists{\mathrm f_m}$}\\ 1+\omega_{s,1}+\omega_{s,2} & \text{else} \end{cases} \]

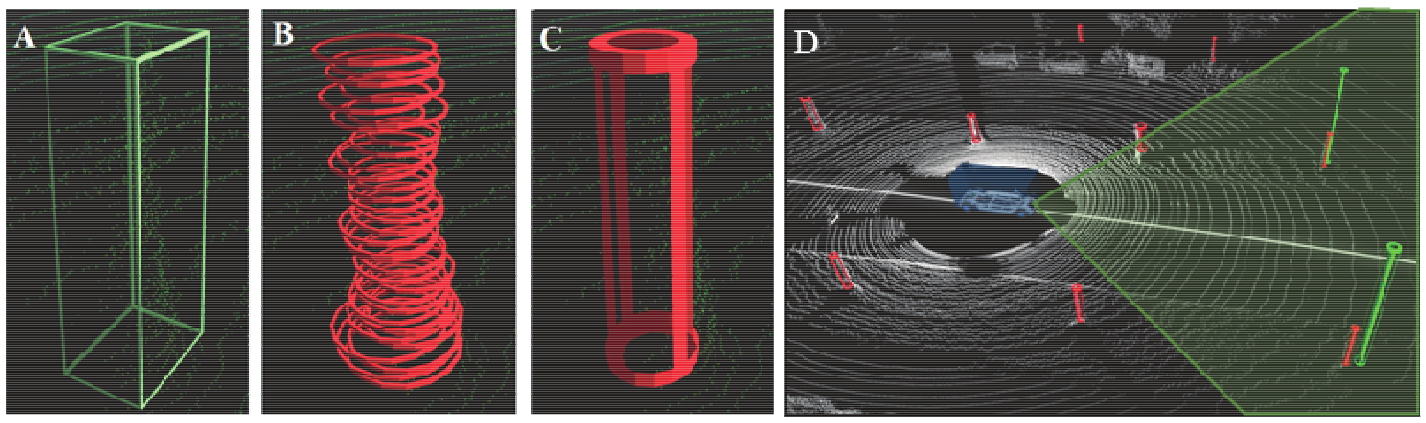
那么，从上式中可以看出，面特征和地面标线的优化目标主要有三部分：距离偏差、角度偏差和不重叠部分的比例。下图给出了这三种优化目标对应的图示：

特征关联首先在GNSS和上一时刻的定位位姿附件采样，由此来产生一组先验位姿。对于每一个先验位姿，都可以计算出一组最优关联和相应的优化目标值。也就是说，只要在这些优化目标值中选取一个最小值，而这个最小值对应的关联即为最优关联$a_k$，这一组关联将陪传入位姿优化层进行位姿优化。

五、位姿优化

与一般的定位算法不同，这篇论文在位姿优化时，并不是值优化当前帧对应的位姿，而是连带前\(N-1\)帧数据一起进行优化。优化目标主要有两个：里程计和特征关联。

优化残差

里程计残差表达式如下：

\[r({\mathrm p_i}, {\mathrm p_{i+1}}) = ({\mathrm p^{-1}_{i+1}}{\mathrm p_i}) \triangle_{i \rightarrow i+1} \]

上式中，\(\triangle_{i \rightarrow i+1}\)即为里程计从\(i\)时刻到\(i+1\)时刻的测量值。
而特征关联的残差表达式为：

\[r(a_k, {\mathrm p_i}) = \begin{cases} \omega_1 d_p(a_k, {\mathrm p_i}) & \text{for poles}\\ \omega_2 d_s(a_k, {\mathrm p_i}) + \omega_3 \triangle\alpha_s(a_k, {\mathrm p_i}) & \text{else} \end{cases} \]

对于杆特征而言，只需要优化对应的距离残差，而对于面特征和地面标线则还需优化角度残差，距离与角度的定义与特征关联时的定义相同。论文中，残差优化的方法采用的是LM算法，而且作者还提到：考虑到算法的实时性，每次优化并不是直到收敛才停止，而是根据需要设置固定的优化时长。

异常值处理

为了防止因误匹配等原因造成的残差过大，从而使得优化不能收敛，该论文所采用的优化函数并非常用的最小二乘优化函数(\(min\frac{1}{2}\sum_i r_i^2\))，而是在此基础上引入柯西核函数(Cauchy -loss function)，也即：

\[min\frac{c^2}{2}\sum_i log(1+(\frac{r_i}{c})^2) \]

这样，即使出现残差值异常的情况，目标函数也不会引起太大的变化。
此外，在优化的初始化阶段，柯西核函数是不激活的，这样做是希望较大的残差能够使优化快速收敛。至于何时激活柯西核函数，则需要根据较小残差数占总残差数的比例来确定：

\[\varepsilon = \frac{|\{r(a_k)|r(a_k) \in W_o \wedge r(a_k) < T_a\}|}{|\{r(a_k)|r(a_k) \in W_o\}|} \]

那么，只有当\(\varepsilon > T_{\varepsilon}\)时，柯西核函数才会被激活。