线性回归如何一次性达到最优。
其实很简单,求出线性回归表达式的解析解就好了,还不需要使用梯度下降法。
方法如下:
假设损失函数为(推导提示看文末图):
\(J(θ) = \frac{1}{2}\sum_{i=1}^n(h_θ(x^{(i)}-y^{(i)})^2=\frac{1}{2}(X\theta-Y)^T(X\theta-Y)\tag{1}\)
矩阵展开后:
\[\begin{aligned}
J(\theta) &= \frac{1}{2}(\theta^TX^T-Y^T)(X\theta-Y)\\
&=\frac{1}{2}(\theta^TX^TX\theta-\theta^TX^TY-Y^TX\theta+Y^TY)
\end{aligned}\]
对\(J(\theta)\)关于\(\theta\)求导:
\[\frac{\alpha J(\theta)}{\alpha\theta} = \frac{1}{2}(2X^TX\theta-X^TY-X^TY)=0
\]
\[X^TX\theta-X^TY=0
\]
\[X^TX\theta=X^TY
\]
求得:
\[\theta=(X^TX)^{-1}X^TY
\]
所以只是一个线性回归器的话,我们可以把整个数据集运用到其上面,一步得到最优解。
代码实践
首先我们定义输入和输出:
假设:
\[\begin{aligned}
y&=2X+3+\xi,\\
X&=[\begin{matrix} x_0&x_1&x_2&\cdots \end{matrix}]
\end{aligned}\]
其中\(\xi∼N(0,1)\),
化为矩阵形式为:
\[y=[\begin{matrix} 2&3\end{matrix}]
\left[\begin{matrix} x_0&x_1&x_2& \cdots\\1&1&1&\cdots\end{matrix}\right]+
\xi
\]
代码为:
X = torch.concat([torch.arange(0,20,0.1).view(-1,1),torch.ones(200).view(-1,1)],dim=-1)
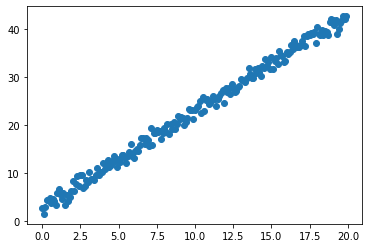
y = torch.tensor([2,3],dtype=torch.float)@X.T+torch.randn(size=(200,))
可视化如下:
首先我们求出\(\theta\)的解析解:
theta = torch.inverse(X.T@X)@X.T@y
tensor([2.0043, 2.8775])
然后我们通过sklearn看看线性回归模型拟合后的系数:
model = LinearRegression(fit_intercept=False)
model.fit(X=X,y=y)
model.coef_
array([2.0042787, 2.8774676], dtype=float32)
再来看看用pytorch中的Linear模块训练出的模型的拟合情况:
model = torch.nn.Linear(in_features=2,out_features=1,bias=False)
optimizer = AdamW(model.parameters(),lr=1e-1)
losses = []
for epoch in range(1000):
logits = model(X).view(-1)
loss = torch.nn.functional.mse_loss(model(X).view(-1),y)
loss.backward()
losses.append(loss.item())
optimizer.step()
optimizer.zero_grad()
训练后,查看模型参数:
dict(model.named_parameters())
{'weight': Parameter containing:
tensor([[2.0057, 2.8103]], requires_grad=True)}
下面的表格展示了三种方法对应的最小loss:
| method | parameters | mse loss |
|---|---|---|
| 解析解 | [2.0043, 2.8775] | 0.9377 |
| sklearn | [2.0042787, 2.8774676] | 0.9377 |
| Pytorch | [2.0057, 2.8103] | 0.9377844929695129 |
另外,如果
\[y=[\begin{matrix} 2&3\end{matrix}]
\left[\begin{matrix} x_0&x_1&x_2& \cdots\\1&1&1&\cdots\end{matrix}\right]
\]
那么三种方法对应的最小loss则为:
| method | parameters | mse loss |
|---|---|---|
| 解析解(0.7s) | [2.0000, 3.0000] | 4.6930e-12 |
| sklearn(0.6s) | [1.9999994, 2.9999995] | 5.3014e-11 |
| Pytorch(迭代1万次)(4s) | [2.0023, 2.9671] | 0.0002794999163597822 |
| Pytorch(迭代3万次)(12s) | [2.0000, 3.0000] | 4.183675704049622e-13 |
式(1)推导提示
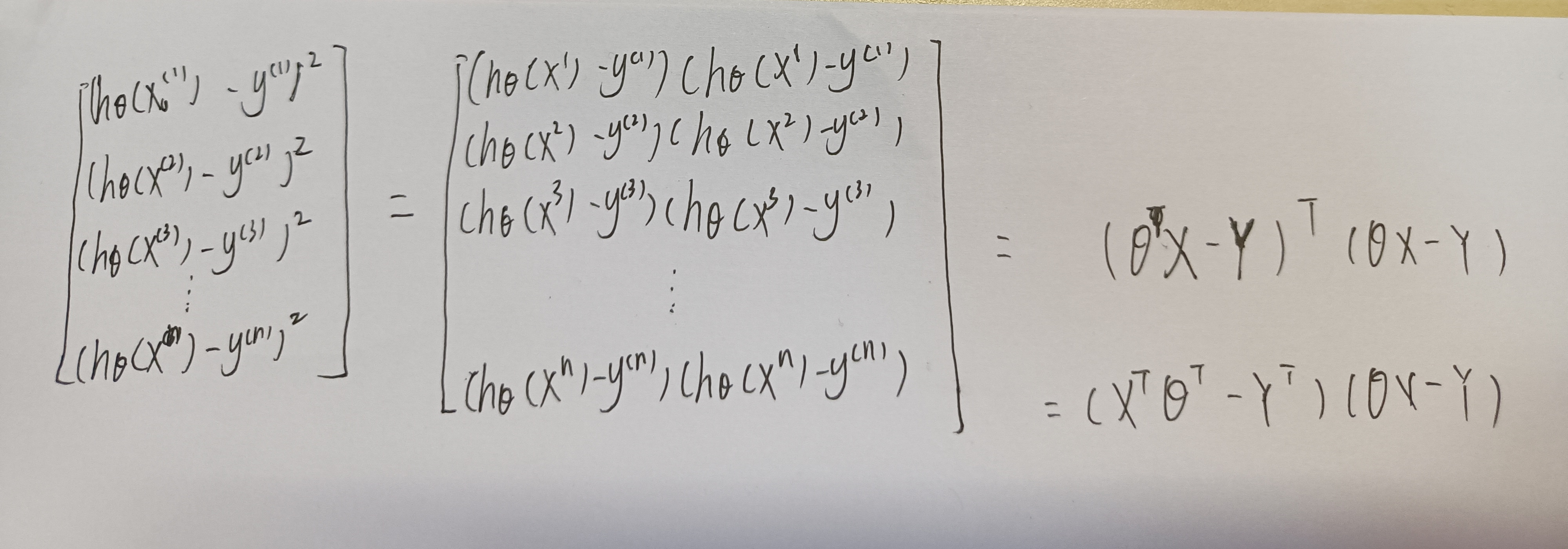

 浙公网安备 33010602011771号
浙公网安备 33010602011771号