密码学作业要求提交个人博客,所以出现了这篇混乱的博客,因为是直接把平时的markdown直接粘的。本文的题目不是按照三个实验的顺序,而是根据现代密码课程,大致按照几个密码类型(比如stream、block、hash这样)进行记录的,但题目都是课上或者coursera上出现的,有兴趣的可以参考一下。有机会我会把几个模块单独拿出来分享。至于代码,我大多放的是片段,而且库都不全,看个思路还可以,想直接运行还是难了点。因为不想误人子弟所以出现了这段前言,看到这还没叉掉的话,那就请点开目录随便看看吧,感谢支持!
Programming Assignment
感谢几个大跌网站
密码数论实现GitHub - dasuntheekshanagit/Number-Theory-and-Cryptography at patch-1
很多内容实用密码学 (practicalcryptography.com)
单表替换的在线解密网站quipqiup - cryptoquip and cryptogram solver
重合指数法破解维吉尼亚密码(英文文本) | Clang裁缝店 (xuanxuanblingbling.github.io)
完成张老师作业的往届优秀学长yikesoftware/cryptography_assignment: 《现代密码学》大作业 (github.com)
cryptopals的wpMy Cryptopals Write-Up (cedricvanrompay.gitlab.io)
youtube的codeHilb3r7/cryptopals: Solutions to the cryptopals challenges in python3 (github.com)
解欧拉计划的博客ProjectEuler 趣题汉化 - 飲水思源 - A man, a plan, a canal, Panama. (is-programmer.com)
vigenere
雨课堂第一次作业/PA1 option
Recovered the original plaintext
Write a program that allows you to "crack" ciphertexts generated using a Vigenere-like cipher, where byte-wise XOR is used instead of addition modulo 26.
编写一个程序,允许您“破解”使用类似vigenere的密码生成的密文,其中使用逐字节异或而不是加法模26。具体来说,就是密文是通过使用下面的C程序加密英文文本生成的。(当然,在加密时,我使用随机密钥长度并随机选择密钥的每个字节。) 明文包含大写字母、小写字母、标点符号和空格,但不包含数字。
Of course, when encrypting I used a random key length and chose each byte of the key at random.) The plaintext contains upper- and lower-case letters, punctuation, and spaces, but no numbers.
Specifically, the ciphertext was generated by encrypting English-language text using the following C program:
#include <stdio.h> #define KEY_LENGTH 2 // Can be anything from 1 to 13 main(){ unsigned char ch; FILE *fpIn, *fpOut; int i; unsigned char key[KEY_LENGTH] = {0x00, 0x00}; /* of course, I did not use the all-0s key to encrypt */ fpIn = fopen("ptext.txt", "r"); fpOut = fopen("ctext.txt", "w"); i=0; while (fscanf(fpIn, "%c", &ch) != EOF) { /* avoid encrypting newline characters */ /* In a "real-world" implementation of the Vigenere cipher, every ASCII character in the plaintext would be encrypted. However, I want to avoid encrypting newlines here because it makes recovering the plaintext slightly more difficult... */ /* ...and my goal is not to create "production-quality" code =) */ if (ch!='\n') { fprintf(fpOut, "%02X", ch ^ key[i % KEY_LENGTH]); // ^ is logical XOR i++; } } fclose(fpIn); fclose(fpOut); return; }
re.sub("[^a-zA-Z ]","",cipher)对每个字符串应用正则表达式操作,删除所有非字母字符
import string
strmi='F96DE8C227A259C87EE1DA2AED57C93FE5DA36ED4EC87EF2C63AAE5B9A7EFFD673BE4ACF7BE8923C\
AB1ECE7AF2DA3DA44FCF7AE29235A24C963FF0DF3CA3599A70E5DA36BF1ECE77F8DC34BE129A6CF4D126BF\
5B9A7CFEDF3EB850D37CF0C63AA2509A76FF9227A55B9A6FE3D720A850D97AB1DD35ED5FCE6BF0D138A84C\
C931B1F121B44ECE70F6C032BD56C33FF9D320ED5CDF7AFF9226BE5BDE3FF7DD21ED56CF71F5C036A94D96\
3FF8D473A351CE3FE5DA3CB84DDB71F5C17FED51DC3FE8D732BF4D963FF3C727ED4AC87EF5DB27A451D47E\
FD9230BF47CA6BFEC12ABE4ADF72E29224A84CDF3FF5D720A459D47AF59232A35A9A7AE7D33FB85FCE7AF5\
923AA31EDB3FF7D33ABF52C33FF0D673A551D93FFCD33DA35BC831B1F43CBF1EDF67F0DF23A15B963FE5DA\
36ED68D378F4DC36BF5B9A7AFFD121B44ECE76FEDC73BE5DD27AFCD773BA5FC93FE5DA3CB859D26BB1C63C\
ED5CDF3FE2D730B84CDF3FF7DD21ED5ADF7CF0D636BE1EDB79E5D721ED57CE3FE6D320ED57D469F4DC27A8\
5A963FF3C727ED49DF3FFFDD24ED55D470E69E73AC50DE3FE5DA3ABE1EDF67F4C030A44DDF3FF5D73EA250\
C96BE3D327A84D963FE5DA32B91ED36BB1D132A31ED87AB1D021A255DF71B1C436BF479A7AF0C13AA14794'
def findindexkey2(subarr):#筛选密钥
test_chars=string.ascii_letters+string.digits+','+'.'+' '#将检查的字符改为英文+数字+逗号+句号+空格
#print(test_chars)
test_keys=[]#用于测试密钥
ans_keys=[]#用于结果的返回
for x in range(0x00,0xFF):# 枚举密钥里所有的值
test_keys.append(x)
ans_keys.append(x)
for i in test_keys:
for s in subarr:
if chr(s^i) not in test_chars:
ans_keys.remove(i)#去掉ans_keys里测试失败的密钥
break
#print(ans_keys)
return ans_keys
arr=[]#密文,每个元素为字符的ascii码
for x in range(0,len(strmi),2):
arr.append(int(strmi[x:2+x],16))
vigenerekeys=[]#维基尼尔密码的密钥
for index in range(0,7):
subarr=arr[index::7]
vigenerekeys.append(findindexkey2(subarr))
pt=''
for i in range(0,len(arr)):
pt = pt +chr(arr[i]^vigenerekeys[i%7][0])
print(pt)
guess the key length
frequencies = {
"e": 0.12702, "t": 0.09056, "a": 0.08167, "o": 0.07507, "i": 0.06966,
"n": 0.06749, "s": 0.06327, "h": 0.06094, "r": 0.05987, "d": 0.04253,
"l": 0.04025, "c": 0.02782, "u": 0.02758, "m": 0.02406, "w": 0.02360,
"f": 0.02228, "g": 0.02015, "y": 0.01974, "p": 0.01929, "b": 0.01492,
"v": 0.00978, "k": 0.00772, "j": 0.00153, "x": 0.00150, "q": 0.00095,
"z": 0.00074
}
#猜测密钥长度
def guesskeylenth(cipher,keylenth):
cipher = cipher.lower()
cipher = re.sub("[^a-zA-Z ]","",cipher)
estimatelist = []
for i in range(keylenth):
i += 1
tablelength = i
m = []
for j in range(i):
mm = ""
for k in range(int(len(cipher)/i)):
try:
mm += cipher[j+i*k]
except:
break
m.append(mm)
#print "---------"
sumlist = []
for c in m:
result = {}
for i in c:
result[i] = (c.count(i))/float(len(c))
#print result
sum = 0
for i in result:
sum += result[i]*result[i]
sumlist.append(sum)
print ("[+] 猜测密码长度为: "+str(tablelength)+" 时的概率表")
print (sumlist)
print ("")
estimate = 0
for i in sumlist:
estimate += (i-0.065)*(i-0.065)
estimate /= len(sumlist)
estimatelist.append(estimate)
tmp = []
for i in estimatelist:
tmp.append(i)
#print estimatelist
r1 = estimatelist.index(min(tmp))+1
tmp.remove(min(tmp))
r2 = estimatelist.index(min(tmp))+1
tmp.remove(min(tmp))
r3 = estimatelist.index(min(tmp))+1
tmp.remove(min(tmp))
print ("[+] 概率接近0.065的密码长度:")
print (r1,r2,r3)
return r1,r2,r3
def Vigenere_crack(cipher,keymaxlength=14):
maylenth = guesskeylenth(cipher,keymaxlength)
returnvalue = {}
print ("--------------------------- 解密 ---------------------------")
for may in maylenth:
s = divide(cipher,may)
print('s=',s)
key = ""
message = []
me = ""
print ("[+] 当密码长度为:"+str(may))
for i in s :
k,m = Shift_crack(i)
key += chr(k%26+97)
message.append(m)
for i in range(int(len(message[0]))):
for j in range(may):
me += message[j][i]
returnvalue[key] = me
print ("[+] 密码为: " + key)
print ("[+] 明文为: " + me)
print ("")
return returnvalue
def Vigenere_force(cipher,keymaxlength=10):
maylenth = range(keymaxlength)
returnvalue = {}
print ("--------------------------- 爆破 ---------------------------")
for may in maylenth:
may += 1
s = divide(cipher,may)
key = ""
message = []
me = ""
print ("[+] 当密码长度为:"+str(may))
for i in s :
k,m = Shift_crack(i)
key += chr(k%26+97)
message.append(m)
for i in range(len(message[0])):
for j in range(may):
me += message[j][i]
returnvalue[key] = me
print ("[+] 密码为: " + key)
print ("[+] 明文为: " + me)
print ("")
return returnvalue
shift cipher
#移位密码的攻击
def Shift_crack(cipher):
b,s = [],[]
cipher = cipher.lower()#转小写
a = re.sub("[^a-zA-Z ]","",cipher)#删除非字母符号,a是cipher
lenth = len(a.replace(" ",""))#计算不含空格的长度
for j in range(26):
c = ""
for i in a:
if i!=" ":#将字符 i 向右移动 j 个位置
c += chr((((ord(i)-97)+j)%26)+97)
else:
c += i#空格照旧添上
b.append(c) #b是密文的所有可能的移位后的密文组列表
for j in b:
d = {}
sum = 0
for i in j:
if i!=" ":
d[i] = j.count(i)/float(lenth) #此情况(j)下密文的字母i出现概率
for i in d: #求和j密文形成的频率表,求重合指数
sum += d[i] * frequencies[i]
# sum += (j.count(i)*(j.count(i)-1))/(float(lenth)*(float(lenth)-1))我学的重合指数
s.append(abs(sum-0.065))
key = 26-s.index(min(s))
message = b[s.index(min(s))]
return key,message
OTP
coursera week1 problem7
Suppose you are told that the one time pad encryption of the message"attack at dawn" is 09e1c5f70a65ac519458e7e53f36
(the plaintext letters are encoded as 8-bit ASCII and the given ciphertext is written in hex).
What would be the one time pad encryption of the message "attack at dusk" under the same OTP key?
本题考察经典的OTP加密方案,题目已经给出了一组CT-PT
明文:attack at dawn
密文:09e1c5f70a65ac519458e7e53f36
这应该是第一次摸到密码编程题,游戏规则还没摸清楚。简单介绍一下本题的出装规则吧,
PT是八位的ASCII码编码,一个字母两位Hex八位Bin
CT编出来是十六进制形式。
数了也能看出来,明文是14个字符正好密文是28位。
还是基础不牢,复习一下ASCII码表吧
| Bin | Dec | Hex | 字符 |
|---|---|---|---|
| 0010 0000 | 32 | 0x20 | (space) |
| 0011 0000 | 48 | 0x30 | 0 |
| 0100 0001 | 65 | 0x41 | A |
| 0110 0001 | 97 | 0x61 | a |
根据OTP的加解密算法,明文和密文异或即可得到密钥,又说用同一个key,那就密钥再和明文异或得到密文
python程序如下:
def str_to_int(s):
return int(s.encode().hex(), 16)
key = str_to_int("attack at dawn") ^ 0x09e1c5f70a65ac519458e7e53f36
print(hex(str_to_int("attack at dusk") ^ key))
'''
输出结果
0x9e1c5f70a65ac519458e7f13b33
'''
小结,
掌握一下OTP和字符转换吧
s.encode()将输入字符串s编码为字节序列。这是因为在计算机内部,所有的数据都以字节的形式表示。
.hex()将字节序列转换为十六进制字符串。这意味着字节序列中的每个字节都将转换为两个十六进制字符。
int(..., 16)将十六进制字符串转换为整数。第二个参数16表示要使用的进制,这里是十六进制
转换和运算
字节转换相关
给python课摸鱼赎罪
###字符串转字节 encode()
text = "Hello, World!"
byte_data = text.encode('utf-8')
###字节转字符串 decode()
byte_data = b'Hello, World!'
text = byte_data.decode('utf-8')
###十六进制字符串转字节 bytes.fromhex()
hex_string = "48656c6c6f2c20576f726c6421"
byte_data = bytes.fromhex(hex_string)
###字节转十六进制字符串 hex()
byte_data = b'Hello, World!'
hex_string = byte_data.hex()
###整数转字节 to_bytes()
integer_value = 42
byte_data = integer_value.to_bytes(2, byteorder='big')
###字节转整数 int.from_bytes()
byte_data = b'\x00\x2a'
integer_value = int.from_bytes(byte_data, byteorder='big')
###进制转换
hexadecimal_string = '2a'
decimal_number = int(hexadecimal_string, 16)#转十进制
hex_number = "1A"
binary_number = bin(int(hex_number, 16))[2:]#转二进制(十六->十/int->二进制)
decimal_number = 42
hexadecimal_number = hex(decimal_number)#转十六进制
###整数(ASCII码)转换成字符 chr()
c = chr(b ^ ct_bytes[index] ^ c_byte)
###字符串转ASCII码 ord()
ord() 来获取字符 char 的ASCII码值(整数)。例如,ord('a') 返回97
Python 允许你对 bytes 对象中的每个字节进行按位异或操作,而不需要显式循环遍历每个字节
src = bytes.fromhex('1c0111001f010100061a024b53535009181c')
mask = bytes.fromhex('686974207468652062756c6c277320657965')
result = xor_bytes(src, mask)
result_hex = result.hex()
不能写 print(bytes(pt))要写pt.encode('utf-8')
字节初始化pt = bytearray()
key = b"ICE",如果要异或使用的key[0]的类型是int,也就是说这种形式可以直接result = bytes([x ^ y for x, y in zip(ct, key)])
sha1(codecs.decode(d, "hex")).hexdigest()是个字符串
-
codecs模块的decode函数,它用于解码数据,将以十六进制表示的字符串d解码为原始的字节数据。hex->bytes但是没必要,直接使用
bytes.fromhex()一个效果 -
sha1()接受byte对象作为输入,生成20字节的哈希值 -
sha1().hexdigest()将二进制的哈希转换为十六进制字符串
模指数

def modExponentiation(b, e, m):
c = 1
i = 0
while i < e:
c = (c * b) % m
i += 1
return c
def mod_pow(base, exponent, n):
mul = 1
base = base % n
while exponent > 1:
# odd
if exponent % 2:
mul = (mul * base) % n
exponent -= 1
exponent = exponent // 2
base = (base * base) % n
return (base * mul) % n
XOR - set1
'''将十六进制转换为 base64'''
import base64
string = "49276d206b696c6c696e6720796f757220627261696e206c696b65206120706f69736f6e6f7573206d757368726f6f6d"
byte_data = bytes.fromhex(string)
print(byte_data)
base = base64.b64encode(byte_data)
print(base)
'''本题要点
Always operate on raw bytes, never on encoded strings.
Only use hex and base64 for pretty-printing.
在处理二进制数据时,应该直接使用原始字节数据,
而不是在处理过程中将其转换为字符串
'''
'''Fixed XOR
Write a function that takes two equal-length buffers and produces their XOR combination.
If your function works properly, then when you feed it the string "s1"
after hex decoding, and when XOR'd against "s2"
should produce "expected"
'''
def turn(input):
new = bin(int(input,16))[2:]
return new
def XOR(input1,input2):
result = ''
# tag = 0
# while(tag < len(input1)):
# codea = input1[tag:tag+2]
# codeb = input2[tag:tag+2]
# result += hex(int(codea, 16) ^ int(codeb, 16))[2:].zfill(2)
# tag +=2
#突然想起来,虽然两片有实际意义,但实质都是逐位异或,何必切两片,切一片更方便
for i in range(len(input1)):
codea = input1[i]
codeb = input2[i]
result += hex(int(codea, 16) ^ int(codeb, 16))[2:]
return result
s1 = "1c0111001f010100061a024b53535009181c"
s2 = "686974207468652062756c6c277320657965"
result = XOR(s1,s2)
print(result)
expected = '746865206b696420646f6e277420706c6179'
if result == expected:
print("yes, equal!")
else:
print('no')
'''总结
这里还是练习对原始的数据类型的熟悉和掌握'''
'''
repeating-key XOR
pt = "Burning 'em, if you ain't quick and nimble
I go crazy when I hear a cymbal"
Encrypt it, under the key "ICE", using repeating-key XOR. XOR btyes
'''
def venerge(ct,key):
pt = ''
for i in range(len(ct)):
pt += chr(ct[i]^ key[i % len(key)])
#print(pt.encode('utf-8').hex())
return pt.encode('utf-8').hex()
ct = b"Burning 'em, if you ain't quick and nimble\nI go crazy when I hear a cymbal"
key = b"ICE"
expected = '0b3637272a2b2e63622c2e69692a23693a2a3c6324202d623d63343c2a26226324272765272a282b2f20430a652e2c652a3124333a653e2b2027630c692b20283165286326302e27282f'
print(f"is the pt equal to the expected ? {venerge(ct,key) == expected}")
'''
被字节异或时,变量的数据类型折磨疯了.总结来说,
异或用int,int用chr转str加到pt=""里
str一般在运算中用不到,转成bytes
str.encode(utf-8)有的不是字母直接return出现b'\x0b67\'*+.cb,.i*#i:*<c.,e+ c\x (1e(/'这种表示
所以让他是啥就呈现啥,hex()后print
'''
stream cipher
coursera week1 PA
Many Time Pad
Let us see what goes wrong when a stream cipher key is used more than once.
Below are eleven hex-encoded ciphertexts that are the result of encrypting eleven plaintexts with a stream cipher, all with the same stream cipher key.
Your goal is to decrypt the last ciphertext, and submit the secret message within it as solution.
Hint: XOR the ciphertexts together, and consider what happens when a space is XORed with a character in [a-zA-Z].
给出11条密文如下
'315c4eeaa8b5f8aaf9174145bf43e1784b8fa00dc71d885a80…', '234c02ecbbfbafa3ed18510abd11fa724fcda2018a1a8342cf…', '32510ba9a7b2bba9b8005d43a304b5714cc0bb0c8a34884dd9…', '32510ba9aab2a8a4fd06414fb517b5605cc0aa0dc91a8908c2…', '3f561ba9adb4b6ebec54424ba317b564418fac0dd35f8c08d3…', '32510bfbacfbb9befd54415da243e1695ecabd58c519cd4bd2…', '32510bfbacfbb9befd54415da243e1695ecabd58c519cd4bd9…', '315c4eeaa8b5f8bffd11155ea506b56041c6a00c8a08854dd2…', '271946f9bbb2aeadec111841a81abc300ecaa01bd8069d5cc9…', '466d06ece998b7a2fb1d464fed2ced7641ddaa3cc31c9941cf…', '32510ba9babebbbefd001547a810e67149caee11d945cd7fc8…']
最后一条是待破解的
本题考查针对OTP的多次密码攻击,由于模二加是跟自己的对偶计算,具有很好的同态性,如果一个密钥被多个密文使用,那么这些密文进行异或,XOR 操作会抵消密钥流,得到的就是这些明文进行的异或结果。
采用其中一个密文并将其与其他每个密文进行 XOR 运算。最终会得到对应于所选密文的明文与其他每个明文进行的 XOR 运算。
现在依次查看每个位置。假设所选明文中该位置的字符可能是字母或空格。
- 如果它是一个空格,则成对 XOR 明文中该位置的字符将是字母(如果另一个明文中该位置的字符是字母)或空值(如果两个字符都是空格)。
- 如果是字母,则成对 XOR 明文中该位置的字符将是随机控制字符(如果另一个明文中该位置的字符是大小写相同的字母)、数字或标点符号(如果另一个字符是大小写不同的字母)或大小写翻转的特定字母(如果另一个字符是空格)。
测,直接英翻根本看不懂,读了代码我的理解如下,核心计算就是把target的密文和其他某行密文异或,这样相当于两个明文异或,然后我猜那个某行明文只可能是大小写空格,这样我就再异或上一遍ascii,把那个明文消去,只剩下target,但是这只是我猜另一个明文是某字母的情况下的可能,不太准确,所以需要遍历这一个index列下的所有密文(穷举就是靠数量多)。我把这个message用字母空格猜一遍得出来的target的字母表(最里层的for)和再猜那个message在ASCII跑一遍得到的字母表,这些message加一起我就能得到频次表,把可能性最大的那个字母搞出来。
import string
cipher_texts = ('','','')##密文列表
ct_len = len(bytes.fromhex(cipher_texts[-1]))#最后一个密文的长度
ct_bytes_list = [bytes.fromhex(ct) for ct in cipher_texts]#密文的字节表示
pt = ''
#迭代处理最后一个密文的每个字节
for index, b in enumerate(ct_bytes_list[-1]):
possible_pts = {}#存储待解密明文的字典
#迭代处理其他密文
for i,ct_bytes in enumerate(ct_bytes_list[:-1]):
#判断index超出当前其他密文时,跳出
if index >= len(ct_bytes):
continue
#迭代大小写空格,尝试不同的异或解密
for c_byte in (string.ascii_letters + ' ').encode('ascii'):
#b是最后一个密文,ct_bytes是其他密文,c_byte是ascii里的候选字节
c = chr(b ^ ct_bytes[index] ^ c_byte)
#讨论结果为ascii大小写和:,的字节并记录下来
if c not in string.ascii_letters + ':, ':
continue
if c in possible_pts:
possible_pts[c] += 1
else:
possible_pts[c] = 1
#if i == 9:
# print("It's the last test round for the cipher:",hex(b),"and its pt maybe")
# print(dict(sorted(possible_pts.items(), key=lambda item: item[1], reverse=True)))
pt += max(possible_pts, key=possible_pts.get)
print(pt)
###输出
###The secuet message is: Whxn using a stream cipher, never use the key more than once
BM算法
Berlekamp-Massey algorithm用来构造一个尽可能短的线性反馈移位寄存器LFSR来产生一个有限二元序列




求生成以下二进制序列的最短LFSR的特征多项式
a) (10010000111101000011100000011)
b) (00001110110101000110111 100011)
c) (101011110100010010101 11100010)
它可以概括为找到多项式Λ(x)的系数Λj,以便对于输入流S中的所有位置i:
C(x)是Λ(x)的潜在实例。L个误差的误差定位多项式C(x)定义为:
该算法的目标是确定导致所有特征的最小度L和C(x)
block cipher
01-2轮Feistel网络

可以看的出,两次加密中,如果Left部分是0串和1串且Right部分相同,1轮feistel后,R部分互反,第2轮后L部分继承上轮R,输出的message的Lift32bit互反(例如“e86d2de2 e1387ae9”-“1792d21d b645c008”)
02-CBC/CTR的错误率
加密message:m,AES分组个数为l,密文传输错误块l/2。当ct被接受解密后,有多少明文块也被破坏
- CBC mode
2个——每个ct块只会影响当前明文和下一个明文块
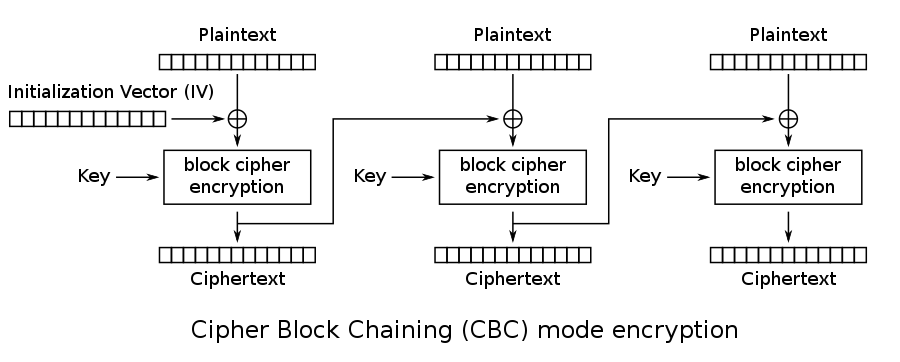

- CTR
1个——每个ct块只影响当前明文块
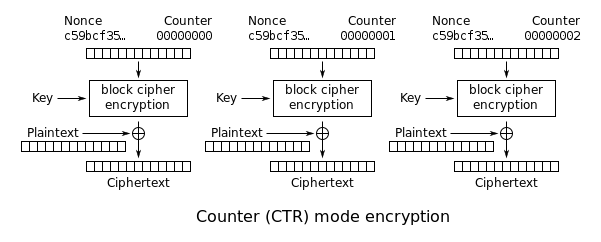

03-侧信道攻击
加密系统并不能完全隐藏传播的消息。泄露
web请求的长度已经被用来窃听一些网站的加密的HTTPS流量,如报税网站,谷歌搜索,医疗网站。
假设攻击者拦截了一个数据包,他知道数据包的有效载荷使用AES在CBC模式下进行加密,带有随机IV的加密报文负载为128字节。下列哪项Messages似乎是有效载荷的解密——
解法:对比每个message的长度,padding后再加上IV的16Bytes,看哪个能达到128Bytes
04-Implement PKCS#7 padding
Challenge 9 Set 2 - The Cryptopals Crypto Challenges
此题是道基本编程题,简单到懒得问题重述,就是去实现PKCS#7的padding,甚至可以去密码库抄抄
def pkcs7_pad(stream: bytes, block_size: int) -> bytes:
pad_len = block_size - (len(stream) % block_size)
return stream + bytes([pad_len] * pad_len)
def unpad(padded: bytes, block_size: int) -> bytes:
if len(padded) % block_size != 0:
raise ValueError("Input data is not padded")
if not _is_valid_padding(padded):
raise ValueError("Not valid padding")
return padded[:-padded[-1]]
def _is_valid_padding(padded: bytes) -> bool:
pad = padded[-1]
return padded[-pad:] == bytes([pad]) * pad
原本跟pkcs7_pad对应的解密实现如下,但代码不太好读,流放!
def pkcs7_unpad(stream: bytes, block_size: int) -> bytes:
if len(stream) % block_size != 0:
raise ValueError('steam length must be a multiply of block_size')
for i in range(block_size, 0, -1):
guessed_padding = stream[-i:]#取末尾的 i 个字节
# check if the guess is valid
padding_vals = set(guessed_padding)#set()可以过滤重复元素
#如果后面i个字节都相同,且数值就是i,就对了
if len(padding_vals) == 1 and padding_vals.pop() == i:
return stream[:-i]#取末尾i位之前的
# no padding was found
raise ValueError('No padding was found!')
05-An ECB/CBC detection oracle
Challenge 11 Set 2 - The Cryptopals Crypto Challenges
Now that you have ECB and CBC working:
Write a function to generate a random AES key; that's just 16 random bytes.
Write a function that encrypts data under an unknown key --- that is, a function that generates a random key and encrypts under it.
The function should look like:
encryption_oracle(your-input) => [MEANINGLESS JIBBER JABBER]Under the hood, have the function append 5-10 bytes (count chosen randomly) before the plaintext and 5-10 bytes after the plaintext.
Now, have the function choose to encrypt under ECB 1/2 the time, and under CBC the other half (just use random IVs each time for CBC). Use rand(2) to decide which to use.
Detect the block cipher mode the function is using each time. You should end up with a piece of code that, pointed at a block box that might be encrypting ECB or CBC, tells you which one is happening.
任务点:
- 随机生成16Bytes的AES密钥,在该key下加密
- 在明文之前附加5-10个字节(随机选择的计数),在明文之后附加5-10个字节
- rand(2)选择ECB还是CBC(随机iv)模式
- 检测函数每次使用的分组密码模式,编写函数指出正在使用的模式
判断ECB和CBC的要点:将加密后的结果 ct 按照AES块大小进行分块,然后检查是否存在相同的块。如果存在相同的块,那么很可能是ECB模式。在CBC模式下,即使有相同的明文块,由于使用了初始化向量(IV),它们也可能被加密成不同的密文块,从而 len(blocks) 和 len(set(blocks)) 的大小相等。而在ECB模式下,相同的明文块始终会加密成相同的密文块,导致 len(blocks) 小于 len(set(blocks))。
#写个Oracle类,实现加密
class EncryptionOracleInterface:
def encrypt(self, data: bytes) -> bytes:
pass
class encryptionOracle(EncryptionOracleInterface):
def __init__(self):
self.history = []
#随机的AES key
self.key = urandom(16)
def encrypt(self, data: bytes) -> bytes:
#给pt增加随机block
pt = urandom(randint(5,10)) + data + urandom(randint(5,10))
#随机选择加密
if randint(0,1):
self.history.append('CBC')
cipher = AES.new(self.key, AES.MODE_CBC)
else:
self.history.append('ECB')
cipher = AES.new(self.key, AES.MODE_ECB)
return cipher.encrypt(pad(pt, AES.block_size))
def ECB_CBC_detector(oracle: type[EncryptionOracleInterface]) -> str:
#加密相同的明文块
data = b'H' * 48
ct = oracle.encrypt(data)
blocks = [ct[i:i+AES.block_size] for i in range(0, len(ct), AES.block_size)]
#set去重
return 'ECB' if len(blocks) != len(set(blocks)) else 'CBC'
oracle = encryptionOracle()
detections = []
for _ in range(10):
detections.append(ECB_CBC_detector(oracle))
print(f"correct? {detections == oracle.history}")
05-1-Byte-at-a-time ECB decryption
- 使用上题的oracle,encrypt就是:ECB加密一个buffer,使用未知但固定的key
- 加密前,先用base64解码一段未知串,把这个加到pt上
- 需要一个函数
AES-128-ECB(your-string || unknown-string, random-key) - 找分组长度——
oracle.encrypt(test)逐渐增加test的长度,由于pad,增到block_size+1,ct不再和之前等长 - 检测是否为ECB——显然是,但代码要写,那就加一个
assert(ECB_CBC_detector(oracle) == 'ECB')
06-cousera week2 PA
implement CBC and CTR modes myself
In this project you will implement two encryption/decryption systems, one using AES in CBC mode and another using AES in counter mode(CTR). In both cases the 16-byte encryption IV is chosen at random and is prepended to the ciphertext.
For CBC encryption we use the PKCS5 padding scheme. While we ask that you implement both encryption and decryption, we will only test the decryption function. In the following questions you are
given an AES key and a ciphertext(both are hex encoded)
goal is to recover the plaintext and enter it in the input boxes provided below
For an implementation of AES you may use an existing crypto library such as PyCrypto(Python), Crypto++(C++), or any other. While it is fine to use the built-in AES functions, we ask that as a learning experience you implement CBC and CTR modes yourself.
完成本题,可以对CBC和CTR甚至EBC有很内核的了解,相当于复现这些加解密模式的过程。
本次完成后,才算是真正开始入门密码的加解密编程,使用python时最大收获是,大佬的代码可远观不可亵玩。import的库往往也是他们写的,pip install pycryptodome后基本上密码算法不需要自己实现,但是一些函数细节还是要注意,例如字符串/字节异或这个从最开始就在联系的东西,我在异或这里要求两串长度相同这里翻了船,一直纠结导入utils库而没有使用其他方法例如 a ^ b for (a, b) in zip(key, ct]
由于千人千面的需求,因地制宜才是最佳实现!
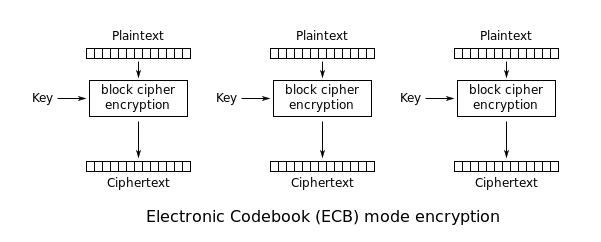
import os
from Crypto.Cipher import AES
class aAES():
def __init__(self,key,mode) -> None:
self.key = bytes.fromhex(key)
self.mode = mode
# mode ->a ``MODE_*`` constant
#最初想法是直接把self.cipher定为AES.new(self.key, self.mode)
#但实际上CTR和CBC的用到AES的加密部分都是ECB,所以cipher定义如下
self.cipher = AES.new(self.key, AES.MODE_ECB)
def decrypt(self,ct):
iv = bytes.fromhex(ct)[:16]
ct_bytes = bytes.fromhex(ct)[16:]
pt = ''
#接下来要分析二者的非共性算法,首先是nonce不一样,CBC就是前一个的ct,CTR需要用到for循环的counter i
#其次AES的加解密不一样,CBC调用AES的解密,用key解ct;CTR调用AES的加密,用key加密nonce
#还有是解pt,逐位异或不同,CBC是每轮iv(前ct)和output;CTR是现ct和output
#最后,padding问题CBC需要解决;CTR不需要(所以异或时加上了[:len(ct_block)])。
#CBC的手动unpad也很酷,pt_block[:-pt_block[-1]],先找到最后一位的数字,直接倒序删除这个数量的padding字节
if self.mode == AES.MODE_CBC:
previous_ct = iv
#密文分组
for i in range(0,len(ct_bytes),16):
ct_block = ct_bytes[i:i+16]
pt_block = [a ^ b for (a, b) in zip(
previous_ct,self.cipher.decrypt(ct_block))]
if i == len(ct_bytes) - 16:#最后一块,处理填充问题
pt_block = pt_block[:-pt_block[-1]]
previous_ct = ct_block
print(pt_block)
pt += ''.join([chr(c) for c in pt_block])
elif self.mode == AES.MODE_CTR:
iv = int.from_bytes(iv, byteorder='big')
for i in range(0,len(ct_bytes),16):
ct_block = ct_bytes[i:i+16]
data = (iv+i//16).to_bytes(16,byteorder='big')
pt_block = [a ^ b for (a, b) in zip(ct_block,self.cipher.encrypt(data)[:len(ct_block)])]
pt += ''.join([chr(c) for c in pt_block])
return pt
def encrypt(self,pt,iv):
pt_bytes = pt.encode('utf-8')
ct = iv
if self.mode == AES.MODE_CBC:
previous_ct = bytes.fromhex(iv)
if len(pt_bytes) % 16 == 0:
pt_bytes += bytes([16]) * 16
for i in range(0,len(pt_bytes),16):
pt_block = pt_bytes[i,i+16]
pad = 16 - len(pt_block)
pt_block += bytes([pad]) * pad
previous_ct = self.cipher.encrypt(bytes([a ^ b for (a, b) in zip(
pt_block,previous_ct)]))
ct += previous_ct.hex()
elif self.mode == 'CTR':
iv = int(iv, 16)
for i in range(0, len(pt_bytes), 16):
pt_block = pt_bytes[i:i+16]
data = (iv+i//16).to_bytes(16, byteorder='big')
ct_block = [a ^ b for (a, b) in zip(
pt_block, self.cipher.encrypt(data)[:len(pt_block)])]
ct += bytes(ct_block).hex()
return ct
07-padding oracle attack
这是crypotals的set3c1题目Challenge 17 Set 3 - The Cryptopals Crypto Challenges
问题重述
结合padding代码和CBC代码,写两个函数
第一个函数应该从以下10个字符串中随机选择一个,生成一个随机的AES密钥(它应该为将来的所有加密保存该密钥),将字符串填充到16字节的AES块大小,并在该密钥下对其进行cbc加密,为调用者提供密文和IV。
第二个函数应该使用第一个函数生成的密文,对其进行解密,检查其填充,并根据填充是否有效返回true或false。
这对函数近似于将AES-CBC加密作为其在web应用程序中部署的服务器端; 第二个函数模拟服务器对加密会话令牌的消费,就好像它是一个cookie一样。
填充Oracle攻击是一种侧信道攻击类型,用于在攻击者可以访问检查密文是否具有有效padding的Oracle时,恢复使用AES-CBC加密的消息的明文。"Oracle" 是指一个能够提供有关密文填充是否正确的信息的服务、函数或组件。这个"Oracle"通常是一个被动攻击者可以访问的接口,攻击者可以向它提交加密的消息,并根据返回的响应(通常是成功或失败)来推断密文的填充是否正确。

Padding Oracle Attack(填充提示攻击)详解及验证 - 简书 (jianshu.com)
首先,依次将初始化向量最后一个字节从0x01~0xFF递增,直到解密的明文最后一个字节为0x01,成为一个正确的padding,unpad不再报错,知道IV和IV^pt,这样也就知道了pt。再改变IV使得最后一个字节异或后为0x02,去试倒数第二字节,这样获得pt。
import AES
from padding import pad, unpad
from utils import xor
from os import urandom
from base64 import b64decode
import random
class paddingOracle:
def __init__(self):
self.key = urandom(16)
self.messages = [
"MDAwMDAwTm93IHRoYXQgdGhlIHBhcnR5IGlzIGp1bXBpbmc=",
"MDAwMDAxV2l0aCB0aGUgYmFzcyBraWNrZWQgaW4gYW5kIHRoZSBWZWdhJ3MgYXJlIHB1bXBpbic=",
"MDAwMDAyUXVpY2sgdG8gdGhlIHBvaW50LCB0byB0aGUgcG9pbnQsIG5vIGZha2luZw==",
"MDAwMDAzQ29va2luZyBNQydzIGxpa2UgYSBwb3VuZCBvZiBiYWNvbg==",
"MDAwMDA0QnVybmluZyAnZW0sIGlmIHlvdSBhaW4ndCBxdWljayBhbmQgbmltYmxl",
"MDAwMDA1SSBnbyBjcmF6eSB3aGVuIEkgaGVhciBhIGN5bWJhbA==",
"MDAwMDA2QW5kIGEgaGlnaCBoYXQgd2l0aCBhIHNvdXBlZCB1cCB0ZW1wbw==",
"MDAwMDA3SSdtIG9uIGEgcm9sbCwgaXQncyB0aW1lIHRvIGdvIHNvbG8=",
"MDAwMDA4b2xsaW4nIGluIG15IGZpdmUgcG9pbnQgb2g=",
"MDAwMDA5aXRoIG15IHJhZy10b3AgZG93biBzbyBteSBoYWlyIGNhbiBibG93"
]
def get_encrypted_message(self) -> bytes:
message = b64decode(random.choice(self.messages))
cipher = AES.new(self.key, AES.MODE_CBC)
return cipher.encrypt(pad(message, AES.block_size))
def is_valid_padding(self, message: bytes) -> bool:
iv = message[:16]
ct = message[16:]
cipher = AES.new(self.key, AES.MODE_CBC, iv)
try:
unpad(cipher.decrypt(ct), AES.block_size)
except:
return False
return True
def recover_plaintext(oracle: paddingOracle, message: bytes) -> bytes:
ct_blocks = [message[i:i+16] for i in range(16, len(message), 16)]
pt = b''
prev_block = message[:16]
for block in ct_blocks:
iv = urandom(16)
keystream = b''
for i in range(1, 17):
for b in range(256):
iv = iv[:16-i] + bytes([b]) + xor(bytes([i]), keystream, length=len(keystream))
if oracle.is_valid_padding(iv + block):##padiing成功
keystream = bytes([b ^ i]) + keystream
break
pt += xor(keystream, prev_block)
prev_block = block
return pt
if __name__ == '__main__':
oracle = paddingOracle()
message = oracle.get_encrypted_message()
pt = recover_plaintext(oracle, message)
print(unpad(pt, AES.block_size))

08-CBC bitflipping attacks
这是set2challenge16Challenge 16 Set 2 - The Cryptopals Crypto Challenges
第一个函数,接受随机输入string,开头插入"comment1=cooking%20MCs;userdata="末尾添加";comment2=%20like%20a%20pound%20of%20bacon"。将输入字符串中的 ";" 和 "=" 字符进行转义【quote out,引用、转义,视为普通字符】,对输入进行填充(pad out)以达到16字节的AES块长度,并使用随机生成的AES密钥对其进行加密。
第二个函数,解密字符串。在解密后的字符串中查找 ";admin=true;" 或者在解密后的字符串上执行拆分操作,将其拆分成2元组,并查找是否存在 "admin" 元组。基于字符串是否存在返回True或False。
不要向第一个函数提供用来生成第二个函数要查找的字符串 user input, 我们得破解密码才能做到相反,可以修改密文(不知道AES密钥)来完成此操作。
依据:CBC模式下,密文块中的1位错误:
- 完全打乱错误发生所在的块
- 在下一个密文块中产生相同的1位错误
字节反转攻击
modification attack on CBC

将前⼀个密文中的任意比特进行修改(0、1进行翻转)。前⼀块的Ciphertext是用来产生下⼀块的明文。如果我们改变了前⼀块Ciphertext中的任意⼀个字节,并与下⼀块解密后的密文进行xor,我们将会得到⼀个不同的明文。重要的是,这个明文是可以由我们所控制。有鉴于此,我们可以选择欺骗服务端或者绕过过滤器进行翻转。
Attacking CBC Mode Encryption: Bit Flipping | by Zhang Zeyu | Medium
针对CBC字节反转攻击的研究与漏洞复现 (baidu.com)
z神的代码
from utils import aes_cbc_encrypt, aes_cbc_decrypt
from Crypto import Random
from Crypto.Cipher import AES
class Oracle:
def __init__(self):
self._key = Random.new().read(AES.key_size[0])
self._iv = Random.new().read(AES.block_size)
self._prefix = "comment1=cooking%20MCs;userdata="
self._suffix = ";comment2=%20like%20a%20pound%20of%20bacon"
def encrypt(self, data):
data = data.replace(';', '').replace('=', '')
plaintext = (self._prefix + data + self._suffix).encode()
return aes_cbc_encrypt(plaintext, self._key, self._iv)
def decrypt_and_check_admin(self, ciphertext):
data = aes_cbc_decrypt(ciphertext, self._key, self._iv)
print(data)
if b';admin=true;' in data:
print("You have successfully logged in!")
else:
print("Something wrong!")
def cbc_bit_flip(encryption_oracle):
block_length = 16
prefix_length = 32
additional_prefix_bytes = (block_length - (prefix_length % block_length)) % block_length
total_prefix_length = prefix_length + additional_prefix_bytes
plaintext = "?admin?true"
additional_plaintext_bytes = (block_length - (len(plaintext) % block_length)) % block_length
final_plaintext = additional_plaintext_bytes * '?' + plaintext
ciphertext = encryption_oracle.encrypt(additional_prefix_bytes * '?' + final_plaintext)
print("ciphertext: ", ciphertext)
semicolon = ciphertext[total_prefix_length - 11] ^ ord('?') ^ ord(';')
equals = ciphertext[total_prefix_length - 5] ^ ord('?') ^ ord('=')
forced_ciphertext = ciphertext[:total_prefix_length - 11] + bytes([semicolon]) + \
ciphertext[total_prefix_length - 10: total_prefix_length - 5] + \
bytes([equals]) + ciphertext[total_prefix_length - 4:]
return forced_ciphertext
def main():
encryption_oracle = Oracle()
forced_ciphertext = cbc_bit_flip(encryption_oracle)
encryption_oracle.decrypt_and_check_admin(forced_ciphertext)
if __name__ == '__main__':
main()
09-CTR bitflipping
Challenge 26 Set 4 - The Cryptopals Crypto Challenges
CTR被认为可以抵抗CBC模式容易受到的比特翻转攻击。
重新实现之前的CBC位翻转练习,使用CTR模式代替CBC模式。 注入一个“admin=true”令牌。
#set4c26my.py
import os
import urllib
from libmatasano import transform_aes_128_ctr, bxor, html_test
# taken from challenge 16 and adapted
class Oracle:
def __init__(self):
self.key = os.urandom(16)
self.nonce = None
def encrypt(self, msg):
# using urllib to quote characters (a bit overkill)
quoted_msg = urllib.parse.quote_from_bytes(msg).encode()
full_msg = (
b"comment1=cooking%20MCs;userdata="+ quoted_msg + b";comment2=%20like%20a%20pound%20of%20bacon"
)
if self.nonce == None:
self.nonce = 0
else:
self.nonce += 1
ciphertext = transform_aes_128_ctr(full_msg, self.key, self.nonce)
return self.nonce, ciphertext
def decrypt_and_check_admin(self, ctxt, nonce):
ptxt = transform_aes_128_ctr(ctxt, self.key, nonce)
if b";admin=true;" in ptxt:
return True
else:
return False
oracle = Oracle()
chosen_plaintext = b'X'*(len(';admin=true'))
nonce, ctxt = oracle.encrypt(chosen_plaintext)
to_xor = (b'\x00'*len(b"comment1=cooking%20MCs;userdata=")
+bxor(b';admin=true', chosen_plaintext))
altered_ctxt = bxor(ctxt, to_xor)
print(transform_aes_128_ctr(altered_ctxt, oracle.key, nonce))
10-Break "random access read/write" AES CTR
Challenge 25 Set 4 - The Cryptopals Crypto Challenges
Back to CTR. Encrypt the recovered plaintext from this file (the ECB exercise) under CTR with a random key (for this exercise the key should be unknown to you, but hold on to it).
Now, write the code that allows you to "seek" into the ciphertext, decrypt, and re-encrypt with different plaintext. Expose this as a function, like, "edit(ciphertext, key, offset, newtext)".
Imagine the "edit" function was exposed to attackers by means of an API call that didn't reveal the key or the original plaintext; the attacker has the ciphertext and controls the offset and "new text".
Recover the original plaintext.
from base64 import b64decode
from itertools import islice
import os
from libmatasano import (
bxor,
transform_aes_128_ctr,
aes_128_ctr_keystream_generator
)
def edit(ctxt, key, offset, newtext):
nonce = 0
keystream = aes_128_ctr_keystream_generator(key, nonce)
new_chunk = bxor(newtext,
islice(keystream, offset, offset+len(newtext)))
result = ctxt[:offset] + new_chunk + ctxt[offset+len(newtext):]
return result
with open('C:\\Users\\lenovo\\Desktop\\crypto\\cryptopals\\25.txt') as f:
data = b64decode(f.read())
key = os.urandom(16)
nonce = 0
#encrypt
ctxt = transform_aes_128_ctr(data, key, nonce)
recovered_keystream = edit(ctxt, key,offset=0,newtext=b'\x00'*len(ctxt))
recovered_plaintext = bxor(ctxt, recovered_keystream)
if recovered_plaintext == data:
print('it\'s the correct plaintext')
else:
print('not correact')
11-Recover the key from CBC with IV=Key
全血细胞计数 - 当静脉注射和钥匙相同时恢复密钥 |贝尔纳多·德·阿劳霍 (bernardoamc.com)
Hash function
AES key 护照信息解密
AES key — encoded in the machine readable zone of a European ePassport
Microsoft Word - Doc.9303.Pt.01.8th.Ed.alltext.en.INPROGRESS.CC.docx (icao.int)
获得一条AES加密消息(CBC模式,初始化向量为零,填充为01-00)。
此外,您已经收到了相应的密钥——不幸的是不太完整——其形式类似身份证件上的机读区(MRZ),例如在欧洲使用电子护照。
目标是找到以下base64编码消息的明文。9MgYwmuPrjiecPMx61O6zIuy3MtIXQQ0E59T3xB6u0Gyf1gYs2i3K9Jx aa0zj4gTMazJuApwd6+jdyeI5iGHvhQyDHGVlAuYTgJrbFDrfB22Fpil2N fNnWFBTXyf7SDI
为了加密,生成并应用了基于基本访问控制(BAC)协议的密钥KENC。为了解密,已经传输了以下字符,KENc可以从这些字符派生(这些字符的编码类型见[1]) :
12345678<8<<<1110182<111116?<<<<<<<<<<<<<<<4
不幸的是,在传输过程中丢失了一个字符,并用“?”突出显示。不过,您可以在[2]的帮助下使其再次可见。为了能够在之后计算密钥Kenc,您可以在[3]、[4]中找到应用的编码协议的概述,并在[5]中找到一个示例。
经过aes加密的消息包含一个要作为解决方案输入的码字。
step1根据护照的校验规则得到MRZ码中?处代表的字符为7
| 1-9护照号码 | 10校验位 | 11-13国家代码 | 14-19持证人生日 | 20生日校验 | 21性别 | 22-27护照有效期 | 28有效期验证码 |
|---|---|---|---|---|---|---|---|
| 12345678< | 8 | <<< | 111018 | 2 | < | 111116 | ? |
校验规则护照 MRZ码编码规则 (itxueyuan.com)
循环赋权重7、3、1,遇<就跳过,求和模10
def Check() -> int:
Check_Number = 0
number = "111116"
weight = "731"
for i in range(0, len(number)):
Check_Number += int(number[i]) * int(weight[i % 3])
return Check_Number % 10
step 2 根据ka,kb生成规则,生成ka,kb,
截取证件号码 出生日期 到期日及校验位计算sha1,取最高有效16字节用作K_seed
#MRZ = 护照号码+校验位+出生日期+校验位+到期日+校验位(包括"<"符号)
MRZ_information = "12345678<811101821111167"
H_information = sha1(MRZ_information.encode()).hexdigest()
K_seed = H_information[0:32]
截取sha1前16字节连结0x00000001计算sha1,结果取前8字节做Ka,8到16字节做Kb
c = "00000001"
d = K_seed + c
H_d = sha1(bytes.fromhex(d)).hexdigest()
ka = H_d[0:16]
kb = H_d[16:32]
step 3 根据ka,kb的奇偶校验对ka,kb进行更改,得到key
def Parity_Check(x):
k_list = []
a = bin(int(x, 16))[2:]
# 16进制字符串转2进制字符串
for i in range(0, len(a), 8):
# 7位一组分块,计算一个校验位,使1的个数为偶数
# 舍弃原来的第8位
if (a[i:i + 7].count("1")) % 2 == 0:
k_list.append(a[i:i + 7])
k_list.append('1')
else:
k_list.append(a[i:i + 7])
k_list.append('0')
k = hex(int(''.join(k_list), 2))
return k
key = Parity_Check(ka)+Parity_Check(kb)
step 4 用key对分组密码解密
ciphertext = base64.b64decode("9MgYwmuPrjiecPMx61O6zIuy3MtIXQQ0E59T3xB6u0Gyf1gYs2i3K9Jxaa0zj4gTMazJuApwd6+jdyeI5iGHvhQyDHGVlAuYTgJrbFDrfB22Fpil2NfNnWFBTXyf7SDI")
IV = '0' * 32
aes_cipher = AES.new(bytes.fromhex(key), AES.MODE_CBC, bytes.fromhex(IV))
m = aes_cipher.decrypt(ciphertext)
print(m.decode())
#Herzlichen Glueckwunsch. Sie haben die Nuss geknackt. Das Codewort lautet: Kryptographie!
SHA1
安全哈希算法1于1995年由美国国家标准与技术研究所标准化,是除MD5之外最常用的哈希算法。使用它的一个例子是基于密码的身份验证。在这种情况下,服务器不会以纯文本形式存储用户密码,而是存储其SHA1哈希值。一旦用户输入了他的密码,在服务器接收到密码后,将计算其哈希值,并将其与存储在服务器上的值进行比较,以验证其正确性。
CRACKING SHA1-HASHED PASSWORDS
场景某监控系统的web服务器漏洞,泄露了管理员账号密码的SHA1哈希值。密码的哈希值为
67ae1a64661ac8b4494666f58c4822408dd0a3e4
此外,登录终端的键盘会显示清楚输入的密码,因为成功登录后,软件中的导航仅通过方向键完成。密码是什么?
给出指纹相当于给出密码的候选字符,爆破的中心思想就是尝试各种排列方式,遍历每个键代表的全部字符可能,确定键-字符后,使用 itertools.permutations 函数生成所有可能的排列,每个排列代表一个候选密码。对于每个候选密码,计算其SHA-1哈希值,并与目标哈希 hash1 进行比较。
#参考https://www.cnblogs.com/elpsycongroo/p/7669786.html
#coding:utf-8
import re
from Crypto.Hash import SHA
import hashlib
import itertools
import datetime
starttime = datetime.datetime.now()
hash1="67ae1a64661ac8b4494666f58c4822408dd0a3e4"
str1="QqWw%58(=0Ii*+nN"
str2=[['Q', 'q'],[ 'W', 'w'],[ '%', '5'], ['8', '('],[ '=', '0'], ['I', 'i'], ['*', '+'], ['n', 'N']]
def sha_encrypt(str):
sha = hashlib.sha1(str)
encrypts = sha.hexdigest()
return encrypts
st3="0"*8
str4=""
str3=list(st3)
for a in range(0,2):
str3[0]=str2[0][a]
for b in range(0,2):
str3[1]=str2[1][b]
for c in range(0,2):
str3[2]=str2[2][c]
for d in range(0,2):
str3[3] = str2[3][d]
for e in range(0,2):
str3[4] = str2[4][e]
for f in range(0,2):
str3[5] = str2[5][f]
for g in range(0,2):
str3[6] = str2[6][g]
for h in range(0,2):
str3[7] = str2[7][h]
newS="".join(str3)
for i in itertools.permutations(newS, 8):
str4 = sha_encrypt(("".join(i)).encode('utf-8'))
if str4==hash1:
print("".join(i))
endtime = datetime.datetime.now()
print((endtime - starttime).total_seconds())
exit(0)
输出
(Q=win*5 5.67901
RSA
欧拉计划——未加密信息
Problem 182 | Project Euler | 欧拉计划 (pe-cn.github.io)
RSA加密流程——
生成两个不同的素数p和q。计算n=pq以及φ=(p-1)(q-1)。
找到整数e,满足1<e<φ,且gcd(e,φ)=1。RSA系统能加密的信息是区间[0,n-1]中的整数。
因此,需要加密的文本首先需要转换成可加密的信息(即区间[0,n-1]内的某个整数)。
加密文本时,如果文本转换成的信息是m,则加密为c=m^e mod n解密过程——
计算d满足ed=1 mod φ,如果加密的信息是c,则解密为m=cd mod n。
存在某些e和m使得me mod n=m。
我们称满足m^e mod n=m的这些m为未加密信息(unconcealed message)对于任意的e,总是存在一些未加密信息。
使得未加密信息的数目为最小值是很重要的。现在我们选择p=1009,q=3643。
找出所有e,满足1<e<φ(1009,3643)且gcd(e,φ)=1,并且此时未加密信息的数目为最小值。求出所有这些e的和。
我的 C++ 欧拉 182 项目解决方案:RSA 加密 (stephan-brumme.com)找到了一个可交互网站,好厉害,但是他说只会复制粘贴答案的是白痴,有被骂到
函数简单,写两个循环判断就好,一个找0-N-1的m,一个要e
'''
https://github.com/nayuki/Project-Euler-solutions/blob/master/python/p182.py
'''
#传N和e,求未加密信息的m的数量
def count_m(modulus, e):
result = 0
for m in range(modulus):
if pow(m, e, modulus) == m:
result += 1
return result
#传N,求所有e
#遍历,用列表,跟φ不互素的置一个10^20,互素的置对应的m的数量
def get_e(prime):
result = []
for e in range(prime - 1):
if math.gcd(e, prime - 1) == 1:
result.append(count_m(prime, e))
else:
result.append(10**20) # Sentinel
return result
#主函数
def main():
P = 1009
Q = 3643
TOTIENT = (P - 1) * (Q - 1)
unconcealed_p = get_e(P)
unconcealed_q = get_e(Q)
min_unconcealed_p = min(unconcealed_p)
min_unconcealed_q = min(unconcealed_q)
#能sum的e的m需要是最小值
ans = sum(e for e in range(TOTIENT) if
unconcealed_p[e % (P - 1)] == min_unconcealed_p and
unconcealed_q[e % (Q - 1)] == min_unconcealed_q)
return str(ans)
if __name__ == "__main__":
start_time = time.perf_counter()
print(compute())
end_time = time.perf_counter()
execution_time = end_time - start_time
print(f"Execution time: {execution_time} seconds")
#ans:399788195976
implement RSA
Challenge 39 Set 5 - The Cryptopals Crypto Challenges即自己写RSA
- Generate 2 random primes. We'll use small numbers to start, so you can just pick them out of a prime table. Call them "p" and "q".
- Let n be p * q. Your RSA math is modulo n.
- Let et be (p-1)*(q-1) (the "totient"). You need this value only for keygen.
- Let e be 3.
- Compute d = invmod(e, et). invmod(17, 3120) is 2753.
- Your public key is [e, n]. Your private key is [d, n].
- To encrypt: c = me%n. To decrypt: m = cd%n
- Test this out with a number, like "42".
- Repeat with bignum primes (keep e=3)
回忆一下block cipher那一部分实现密码系统时的过程,写个RSA类,定义一下参数,加解密方法,差不多就可以了,还有一些零碎的方法实现一下就差不多
from Crypto.Util.number import getPrime
def extended_gcd(a: int, b: int) -> tuple[int, tuple[int, int]]:
"""
Extended Euclidean algorithm
:return: ( 'gcd' - the resulting gcd,
'coeffs' - Bézout coefficients )
a * coeffs[0] + b * coeffs[1] = gcd
"""
old_r, r = a, b
old_s, s = 1, 0
old_t, t = 0, 1
while r != 0:
quotient = old_r // r
old_r, r = r, old_r - quotient * r
old_s, s = s, old_s - quotient * s
old_t, t = t, old_t - quotient * t
return old_r, (old_s, old_t)
def invmod(a: int, m: int):
"""
Modular multiplicative inverse
ax = 1 (mod m)
:return: integer x such that the product ax is congruent to 1 with respect to the modulus m
"""
gcd, coeffs = extended_gcd(a, m)
if gcd != 1:
raise ValueError(f'The modular multiplicative inverse of {a} (mod {m}) does not exist.')
return coeffs[0] % m
class RSA:
def __init__(self, key_len: int = 100):
# key gen
while True:
# repeat until we find et which is co-prime to e
try:
p, q = getPrime(key_len), getPrime(key_len)
n = p * q
et = (p - 1) * (q - 1)
e = 3
d = invmod(e, et)
break
except ValueError:
continue
# keys summery
self.n = n
self.d = d
self.e = e
def encrypt(self, m: bytes) -> int:
m = self.bytes_to_num(m)
c = pow(m, self.e, self.n)
return c
def decrypt(self, c: int) -> bytes:
m = pow(c, self.d, self.n)
m = self.num_to_bytes(m)
return m
@staticmethod
def bytes_to_num(seq: bytes) -> int:
return int(seq.hex(), 16)
@staticmethod
def num_to_bytes(seq: int) -> bytes:
hex_rep = hex(seq)[2:]
hex_rep = '0'*(len(hex_rep) % 2) + hex_rep
return bytes.fromhex(hex_rep)
def main():
rsa_obj = RSA(key_len=1024)
m = b'RSA implementation'
c = rsa_obj.encrypt(m)
print(f'{c=}')
m_rec = rsa_obj.decrypt(c)
print(f'{m_rec=}')
if __name__ == '__main__':
main()
选择题
构造PRG的安全性
PRG安全性,讲的是不可区分性,“PRG生成序列和真随机序列是不可区分的,区分优势可忽略”。
-
答案只给了一句话“a distinguisher for G’ gives a distinguisher for G”,也就是说生成PRG的安全很大情况下依存于题目定义的那个secure PRG,如果构造PRG是在secure PRG上,给序列XOR全1序列、给key XOR一个全1序列,以及抛弃随机序列的最后一位,这都没有改变生成序列的随机性。
-
答案的话术是“a distinguisher will output not random whenever …. ”
需要看出来构造出来的新PRG会在哪里出现规律性的不随机序列。例如
G(k)|G(k)这个构造会导致生成的序列都是前半部分和后半部分相同,这明显不随机;G(k)|0这个构造会使序列最后一位永远是0,这在安全模型中明显易与随机序列可区分;G(0)更抽象了,永远等于G(0).
构造加密算法的SS
加密算法的安全性,依据是语义安全,使用该加密后的密文EXP(0)是否使attcker将与随机序列EXP(1)不可区分。
-
一句话“an attack on E’ gives an attack on E”
-
要说明如何破解的语义安全,“To break semantic security, an attacker would …”
E(0^n,m)攻击者测试0串和1串的加密,可以很容易地区分EXP(0)和EXP(1),因为它知道秘密密钥,即0串。E(k,m)|k攻击者会从挑战密文中读取密钥并使用它来解密挑战密文。 基本上,任何密文都会泄露密钥。E(k,m)|LSB(m)攻击者询问全0串和0..01串,这样就能区分EXP(0)和EXP(1)再次强调,安全是key保证的,攻击者知道整个密码体制的所有细节,包括你直接在这机制里面藏个m藏个key。。太蠢辣
构造PRF的安全性
-
一句话“a distinguisher for F’ gives a distinguisher for F”
-
“This is unlikely to hold for a truly random function. ”
F(k,x)F(k,x11…11)——当询问x=00…00和x=11…11时,输出非随机(应答相同),不太像真随机函数
k^x ——当询问x=00…00和x=11…11时,
k otherwise——询问0串可得k,再询问1串时的F(k,1n)的应答就不再随机(个人理解是函数确定了已经)
MAC1
The MAC signing algorithm S is applied to the file contents and nothing else.
文件交换和修改文件名、上次修改时间不会影响。
但是修改文件内容(增删改)不行;Replacing the tag and contents of one file with the tag and contents of a file from another computer protected by the same MAC system, but a different key.(将一个文件的标签和内容替换为另一台受相同MAC系统保护但密钥不同的计算机上的文件的标签和内容)也不行
构造MAC的安全性
(S,V)是(K,M,T)上的安全MAC。M消息空间n,Ttag空间128,K密钥空间
3.
ECBC-MAC用r作IV,签名算法S(k,m)=(r,ECBCr(k,m)),验证算法V=tag(r,t)(如果t==ECBCr(k,m)输出1)。这个MAC不安全,attacker询问m得到tag(r,t),然后它就可以生成存在性伪造产生:
(r^m,t)对0n
(r^1n,t) 对m^1n
构造认证加密的密文完整性
加密系统(E,D)在(K,M,C)上提供认证加密4+
困难问题
公钥密码理论
没有短密文
使用对称密码可以加密 32 位消息并获取 32 位密文(例如,使用一次性 pad 或使用基于 NONCE 的系统),但具有短密文的公钥系统,永远不可能安全。——攻击者可以使用公钥构建所有2^32个长度为32位的密文解密的字典,使用字典解密任何捕获的密文。
要语义安全就不能det.
let (G,E,D)be a semantically secure public-key encryption system. Can algorithm E be deterministic?
No, semantically secure public-key encryption must be randomized, since otherwise an attacker can easily break semantic security.




 posted on
posted on

 浙公网安备 33010602011771号
浙公网安备 33010602011771号