【ACM】2022.7.31训练赛
A.Arena
CodeForces - 1487A
题目描述
$ n $ heroes fight against each other in the Arena. Initially, the $ i $ -th hero has level $ a_i $ .
Each minute, a fight between two different heroes occurs. These heroes can be chosen arbitrarily (it's even possible that it is the same two heroes that were fighting during the last minute).
When two heroes of equal levels fight, nobody wins the fight. When two heroes of different levels fight, the one with the higher level wins, and his level increases by $ 1 $ .
The winner of the tournament is the first hero that wins in at least $ 100^{500} $ fights (note that it's possible that the tournament lasts forever if no hero wins this number of fights, then there is no winner). A possible winner is a hero such that there exists a sequence of fights that this hero becomes the winner of the tournament.
Calculate the number of possible winners among $ n $ heroes.
输入格式
The first line contains one integer $ t $ ( $ 1 \le t \le 500 $ ) — the number of test cases.
Each test case consists of two lines. The first line contains one integer $ n $ ( $ 2 \le n \le 100 $ ) — the number of heroes. The second line contains $ n $ integers $ a_1, a_2, \dots, a_n $ ( $ 1 \le a_i \le 100 $ ), where $ a_i $ is the initial level of the $ i $ -th hero.
输出格式
For each test case, print one integer — the number of possible winners among the given $ n $ heroes.
样例 #1
样例输入 #1
3
3
3 2 2
2
5 5
4
1 3 3 7
样例输出 #1
1
0
3
提示
In the first test case of the example, the only possible winner is the first hero.
In the second test case of the example, each fight between the heroes results in nobody winning it, so the tournament lasts forever and there is no winner.
翻译【转自洛谷】
n 个英雄在竞技场战斗,初始时第 i 位英雄有能力值 a_i
现在竞技场将进行对决,每分钟都会出现随机的两位(不同的)英雄战斗,最终能力值高的获胜(能力值一样时平局),并且获胜者能力值上升 11(平局时没有英雄的能力值会上升)。
当一位英雄的获胜次数超过 100^500 时,对决结束,该英雄成为赢家。现在请你统计多少英雄可能成为赢家。
T 组数据。
$ 1≤T≤500 $ ;
$ 1≤n,ai ≤ 100 $;
思路
模拟,按照题目给的Notes,可以知道,找出数组a中最小的数的个数,答案就是总个数-最小值的个数
代码
#include <iostream>
#include <cstring>
#include <cstdio>
#include <cmath>
#include <algorithm>
using namespace std;
const int N = 110;
int a[N];
void solve()
{
int n;
cin >> n;
int mina = 0x3f3f3f3f;
for(int i = 1;i <= n;i ++)
{
cin >> a[i];
mina = min(mina , a[i]);
}
sort(a+1,a+n+1);
int ans = 0;
for(int i = 1;i <= n;i ++)
{
if(a[i] != mina)
{
ans = i-1;
break;
}
}
if(ans == 0)
{
cout << 0 << endl;
return ;
}
else
cout << n-ans << endl;
return ;
}
int main()
{
int T;
cin >> T;
while(T --)
solve();
return 0;
}
B.方程的解
计蒜客 A1142
题目描述
给出方程组:
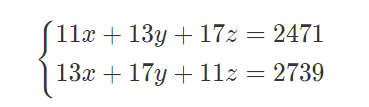
已知 x,y,z 均为正整数,请你计算 x,y,z 相加和最小为多少。
思路
模拟,三重循环,解出答案
代码
#include <iostream>
#include <cstring>
#include <cstdio>
#include <cmath>
#include <algorithm>
using namespace std;
int main()
{
int x , y , z;
for( x = 0;x <= 224;x ++)
{
for( y = 0;y <= 190;y ++)
{
for( z = 0;z <= 249;z ++)
{
int sum1 = 11*x+13*y+17*z;
int sum2 = 13*x+17*y+11*z;
if(sum1 == 2471 && sum2 == 2739)
{
cout << x+y+z << endl;
return 0;
}
}
}
}
return 0;
}
C.Cat Cycle
题目描述
Suppose you are living with two cats: A and B. There are $ n $ napping spots where both cats usually sleep.
Your cats like to sleep and also like all these spots, so they change napping spot each hour cyclically:
- Cat A changes its napping place in order: $ n, n - 1, n - 2, \dots, 3, 2, 1, n, n - 1, \dots $ In other words, at the first hour it's on the spot $ n $ and then goes in decreasing order cyclically;
- Cat B changes its napping place in order: $ 1, 2, 3, \dots, n - 1, n, 1, 2, \dots $ In other words, at the first hour it's on the spot $ 1 $ and then goes in increasing order cyclically.
The cat B is much younger, so they have a strict hierarchy: A and B don't lie together. In other words, if both cats'd like to go in spot $ x $ then the A takes this place and B moves to the next place in its order (if $ x < n $ then to $ x + 1 $ , but if $ x = n $ then to $ 1 $ ). Cat B follows his order, so it won't return to the skipped spot $ x $ after A frees it, but will move to the spot $ x + 2 $ and so on.
Calculate, where cat B will be at hour $ k $ ?
输入格式
The first line contains a single integer $ t $ ( $ 1 \le t \le 10^4 $ ) — the number of test cases.
The first and only line of each test case contains two integers $ n $ and $ k $ ( $ 2 \le n \le 10^9 $ ; $ 1 \le k \le 10^9 $ ) — the number of spots and hour $ k $ .
输出格式
For each test case, print one integer — the index of the spot where cat B will sleep at hour $ k $ .
样例 #1
样例输入 #1
7
2 1
2 2
3 1
3 2
3 3
5 5
69 1337
样例输出 #1
1
2
1
3
2
2
65
提示
In the first and second test cases $ n = 2 $ , so:
- at the $ 1 $ -st hour, A is on spot $ 2 $ and B is on $ 1 $ ;
- at the $ 2 $ -nd hour, A moves to spot $ 1 $ and B — to $ 2 $ .
If $ n = 3 $ then: - at the $ 1 $ -st hour, A is on spot $ 3 $ and B is on $ 1 $ ;
- at the $ 2 $ -nd hour, A moves to spot $ 2 $ ; B'd like to move from $ 1 $ to $ 2 $ , but this spot is occupied, so it moves to $ 3 $ ;
- at the $ 3 $ -rd hour, A moves to spot $ 1 $ ; B also would like to move from $ 3 $ to $ 1 $ , but this spot is occupied, so it moves to $ 2 $ .
In the sixth test case:
- A's spots at each hour are $ [5, 4, 3, 2, 1] $ ;
- B's spots at each hour are $ [1, 2, 4, 5, 2] $ .
题面翻译【转自洛谷】
假设有两只猫:猫 A 和猫 B ,共同拥有 \(n\) 个休息地点排成一个环,位置顺时针编号为 \(1\) 至 \(n\),他们要选择休息位置。
对于选择休息位置,两只猫有不同的策略:
猫 A 在第 \(1\) 小时会选择休息位置 \(n\),接下来每过一小时它就会逆时针移一个位置,也就是说它选择的位置的序列为 \(n,n-1,n-2,...,3,2,1,n,n-1,...\)。
猫 B 在第 \(1\) 小时会选择休息位置 \(1\),接下来每过一小时它就会顺时针移一个位置,也就是说它选择的位置的序列为 \(1,2,3,...,n-1,n,1,2,...\)。
特别的,因为猫 A 比猫 B 老,所以猫 A 比猫 B 地位高一些,因此当两只猫相中了同一个位置时,由猫 A 占领这个位置,猫 B 会再顺时针移一个位置到下一个位置。
给定 \(n,k\),求出第 \(k\) 小时猫 B 在哪个位置。
\(T\) 组询问。
\(1\leq T\leq10^4;2\leq n\leq10^9;1\leq k\leq10^9;\)
思路
按照提示或者题意可以知道
- 当n为偶数时,A和B两只猫,总不会相遇
- 当n为奇数时,A和B两只猫,每隔n/2就会相遇,因此,我们需要将少走的步数加上
代码
#include <iostream>
#include <cstring>
#include <cstdio>
#include <cmath>
#include <algorithm>
#define PI 3.1415926536
using namespace std;
void solve()
{
int n , k;
cin >> n >> k;
if(k == 0)
{
cout << 1 << endl;
return ;
}
if(n % 2 == 0)
{
if(k % n == 0)
cout << n << endl;
else
cout << k%n << endl;
}
else
{
int q = n/2;//每隔q次相遇一次
int z = (k-1) / q;//少走的步数
int m = (z+k) % n;//总共的步数
if(m == 0)
cout << n << endl;
else
cout << m << endl;
}
}
int main()
{
int T;
cin >> T;
while(T --)
solve();
return 0;
}
I. 掎角之势
计蒜客 - A2226
题目描述
在《亮剑》中,李云龙发动的平安战役不仅把晋西北搅成一锅粥,还成为了第二次世界大战的转折点。
晋绥军 358358 团楚云飞得到探报,有大批日军向平安县城移动,于是他准备帮帮场子。友军在平安附近有三个团的兵力,分别是李云龙的独立团,丁伟的新一团,孔捷的新二团,他们三人互成掎角之势。
作为黄埔军校毕业生的楚云飞,对自己的数学非常自信。在研究了友军的防区分布后,想知道李云龙、丁伟、孔捷这三人指挥部位置所形成的三角形的内切圆和外接圆的面积。因为他们的位置是不断变化的,每次重新算一遍很麻烦,想请你编程帮忙来计算。
输入格式
第一行一个整数 T,表示数据的组数。
接下来 T 行,每行 6 个整数 \(x1\),\(y1\),\(x2\),\(y2\),\(x3\),\(y1\) ,分别表示李云龙、丁伟、孔捷这三人指挥部的坐标。
输出格式
对于每组数据,如果不能组成三角形,输出"NO SOLUTION",否则输出两个空格分隔的实数,分别表示内切圆和外接圆的面积。相对误差或者绝对误差在$ 10^{-6} $范围内就认为是正确的。
数据范围
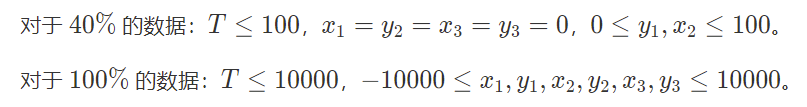
样例
样例输入#1
4
0 3 4 0 0 0
0 0 10 10 -10 -10
3 3 5 3 3 5
0 0 -5 -10 5 -10
样例输出#1
3.1415926536 19.6349540849
NO SOLUTION
1.0780241689 6.2831853072
29.9995403716 122.7184630309
思路
基础的数学运算,本题需要用到的数学公式:
-
计算两点之间的距离:
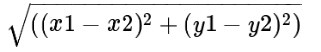
-
已知三边判断三角形是否成立:
-
满足条件两边之和大于第三边
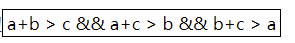
-
判断两条斜率是否不同
x = (x1-x2)*(y1-y3)*1.0;y = (x1-x3)*(y1-y2)*1.0;当 \(x ≠ y\) 时三角形成立
-
计算三角形的面积(利用海伦公式):
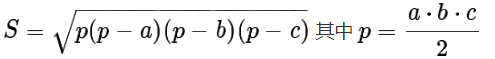
-
内切圆半径与三角形的关系:

-
外接圆半径与三角形的关系:

代码
#include <iostream>
#include <cstring>
#include <cstdio>
#include <cmath>
#include <algorithm>
#define PI 3.1415926536
using namespace std;
void solve()
{
int x1,x2,x3,y1,y2,y3;
scanf("%d%d%d%d%d%d",&x1,&y1,&x2,&y2,&x3,&y3);
double a = sqrt( (x1-x2)*(x1-x2) + (y1-y2)*(y1-y2) );
double b = sqrt( (x1-x3)*(x1-x3) + (y1-y3)*(y1-y3) );
double c = sqrt( (x2-x3)*(x2-x3) + (y2-y3)*(y2-y3) );
double x = (x1-x2)*(y1-y3)*1.0;
double y = (x1-x3)*(y1-y2)*1.0;
if( x != y )
{
double p = (a+b+c)/2;
double S = sqrt(p * (p-a) * (p-b) * (p-c) );
double r1 = (2*S) / (a+b+c);
double r2 = (a*b*c) / (4*S);
printf("%.15f %.15f\n",PI*r1*r1,PI*r2*r2);
}
else
{
cout << "NO SOLUTION" << endl;
return ;
}
}
int main()
{
int T;
cin >> T;
while(T --)
solve();
return 0;
}
K.砝码称重
计蒜客 - T2178
题目描述
设有 1g,2g,3g,5g,10g,20g 的砝码各若干枚(其总重小于等于 1000),现在求问这些砝码能称出多少不同的重量。
输入格式
一行六个整数,分别代表 1g 砝码的个数,分别代表 2g 砝码的个数,分别代表 3g 砝码的个数,分别代表 5g 砝码的个数,分别代表 10g 砝码的个数,分别代表 20g 砝码的个数。
输出格式
输出一行,格式为 Total=n。
(n 表示用这些砝码能称出的不同重量的个数,但不包括一个砝码也不用的情况)
样例
样例输入#1
1 1 0 0 0 0
样例输出#1
Total=3
思路
六重循环,找出可以组成的数。
代码
#include <iostream>
#include <cstring>
#include <cstdio>
#include <cmath>
#include <algorithm>
using namespace std;
const int N = 1010;
bool st[N];
int main()
{
int a[7];
for(int i = 1;i <= 6;i ++)
cin >> a[i];
for(int i = 0;i <= a[1];i ++)
for(int j = 0;j <= a[2];j ++)
for(int k = 0;k <= a[3];k ++)
for(int x = 0;x <= a[4];x ++)
for(int y = 0;y <= a[5];y ++)
for(int z = 0;z <= a[6];z ++)
{
int sum = i*1+j*2+k*3+x*5+y*10+z*20;
st[sum] = true;
}
int cnt = 0;
for(int i = 1;i <= 1000;i ++)
if(st[i])
cnt ++;
cout << "Total=" << cnt << endl;
return 0;
}
D.Dense Array【补】
CodeForces - 1490A
题目描述
Polycarp calls an array dense if the greater of any two adjacent elements is not more than twice bigger than the smaller. More formally, for any $ i $ ( $ 1 \le i \le n-1 $ ), this condition must be satisfied: $ \frac{\max(a[i], a[i+1])}{\min(a[i], a[i+1])} \le 2 $
For example, the arrays $ [1, 2, 3, 4, 3] $ , $ [1, 1, 1] $ and $ [5, 10] $ are dense. And the arrays $ [5, 11] $ , $ [1, 4, 2] $ , $ [6, 6, 1] $ are not dense.
You are given an array $ a $ of $ n $ integers. What is the minimum number of numbers you need to add to an array to make it dense? You can insert numbers anywhere in the array. If the array is already dense, no numbers need to be added.
For example, if \(a=[4,2,10,1]\) , then the answer is $ 5 $ , and the array itself after inserting elements into it may look like this:
$ a=[4,2,\underline{\textbf{3}},\underline{\textbf{5}},10,\underline{\textbf{6}},\underline{\textbf{4}},\underline{\textbf{2}},1] $ (there are other ways to build such $ a$).
输入格式
The first line contains one integer $ t $ ( $ 1 \le t \le 1000 $ ). Then $ t $ test cases follow.
The first line of each test case contains one integer $ n $ ( $ 2 \le n \le 50 $ ) — the length of the array $ a $ .
The next line contains $ n $ integers $ a_1, a_2, \ldots, a_n $ ( $ 1 \le a_i \le 50 $ ).
输出格式
For each test case, output one integer — the minimum number of numbers that must be added to the array to make it dense.
样例 #1
样例输入 #1
6
4
4 2 10 1
2
1 3
2
6 1
3
1 4 2
5
1 2 3 4 3
12
4 31 25 50 30 20 34 46 42 16 15 16
样例输出 #1
5
1
2
1
0
3
提示
The first test case is explained in the statements.
In the second test case, you can insert one element, $ a=[1,\underline{\textbf{2}},3] $ .
In the third test case, you can insert two elements, $ a=[6,\underline{\textbf{4}},\underline{\textbf{2}},1] $ .
In the fourth test case, you can insert one element, $ a=[1,\underline{\textbf{2}},4,2] $ .
In the fifth test case, the array $ a $ is already dense.
题面翻译【转自洛谷】
如果序列 \(a\) 的任意相邻两项中,较大者不大于较小者的二倍,则 Polycarp 称 \(a\) 是一个密集序列。形式化地,序列 \(a\) 是密集的,等价于
例如:序列 \([1, 2, 3, 4, 3]\)、\([1, 1, 1]\)、\([5, 10]\) 是密集的;序列 \([5, 11]\)、\([1, 4, 2]\)、\([6, 6, 1]\) 不是密集的。
你有一个序列 \(a\),你可以在其任意位置插入任意正整数,求最少需要插入多少个数才能使 \(a\) 变为密集的。
例如:\(a = [4, 2, 10, 1]\),则答案为 \(5\),插入后的序列可以为 \(a' = [4, 2, \underline 3, \underline 5, 10, \underline 6, \underline 4, \underline 2, 1]\)。当然还有其他插入数的方式。
\(1 \leqslant t \leqslant 1000\),\(1 \leqslant n \leqslant 50\),\(1 \leqslant a_i \leqslant 50\)。
Translated by KHIN.
思路
模拟,题目可知数据范围不大,因此利用循环进行判断
代码
#include <iostream>
#include <cstring>
#include <cstdio>
#include <cmath>
#include <algorithm>
using namespace std;
const int N = 55;
int a[N];
void solve()
{
int n;
cin >> n;
memset(a,0,sizeof a);
for(int i = 0;i < n;i ++)
cin >> a[i];
int ans = 0;
for(int i = 0;i < n-1;i ++)
{
while(a[i]*2 < a[i+1])
{
a[i] *= 2;
ans ++;
}
while(a[i] > a[i+1]*2)
{
if(a[i] % 2 == 0)
a[i] /= 2;
else
a[i] = a[i] / 2 + 1;
ans ++;
}
}
cout << ans << endl;
}
int main()
{
int T;
cin >> T;
while(T --)
solve();
return 0;
}
E. Balanced Remainders【补】
CodeForces - 1490B
题目描述
You are given a number $ n $ (divisible by $ 3 $ ) and an array $ a[1 \dots n] $ . In one move, you can increase any of the array elements by one. Formally, you choose the index $ i $ ( $ 1 \le i \le n $ ) and replace $ a_i $ with $ a_i + 1 $ . You can choose the same index $ i $ multiple times for different moves.
Let's denote by $ c_0 $ , $ c_1 $ and $ c_2 $ the number of numbers from the array $ a $ that have remainders $ 0 $ , $ 1 $ and $ 2 $ when divided by the number $ 3 $ , respectively. Let's say that the array $ a $ has balanced remainders if $ c_0 $ , $ c_1 $ and $ c_2 $ are equal.
For example, if $ n = 6 $ and $ a = [0, 2, 5, 5, 4, 8] $ , then the following sequence of moves is possible:
- initially $ c_0 = 1 $ , $ c_1 = 1 $ and $ c_2 = 4 $ , these values are not equal to each other. Let's increase $ a_3 $ , now the array $ a = [0, 2, 6, 5, 4, 8] $ ;
- $ c_0 = 2 $ , $ c_1 = 1 $ and $ c_2 = 3 $ , these values are not equal. Let's increase $ a_6 $ , now the array $ a = [0, 2, 6, 5, 4, 9] $ ;
- $ c_0 = 3 $ , $ c_1 = 1 $ and $ c_2 = 2 $ , these values are not equal. Let's increase $ a_1 $ , now the array $ a = [1, 2, 6, 5, 4, 9] $ ;
- $ c_0 = 2 $ , $ c_1 = 2 $ and $ c_2 = 2 $ , these values are equal to each other, which means that the array $ a $ has balanced remainders.
Find the minimum number of moves needed to make the array $ a $ have balanced remainders.
输入格式
The first line contains one integer $ t $ ( $ 1 \le t \le 10^4 $ ). Then $ t $ test cases follow.
The first line of each test case contains one integer $ n $ ( $ 3 \le n \le 3 \cdot 10^4 $ ) — the length of the array $ a $ . It is guaranteed that the number $ n $ is divisible by $ 3 $ .
The next line contains $ n $ integers $ a_1, a_2, \ldots, a_n $ ( $ 0 \leq a_i \leq 100 $ ).
It is guaranteed that the sum of $ n $ over all test cases does not exceed $ 150,000 $ .
输出格式
For each test case, output one integer — the minimum number of moves that must be made for the $ a $ array to make it have balanced remainders.
样例 #1
样例输入 #1
4
6
0 2 5 5 4 8
6
2 0 2 1 0 0
9
7 1 3 4 2 10 3 9 6
6
0 1 2 3 4 5
样例输出 #1
3
1
3
0
提示
The first test case is explained in the statements.
In the second test case, you need to make one move for $ i=2 $ .
The third test case you need to make three moves:
- the first move: $ i=9 $ ;
- the second move: $ i=9 $ ;
- the third move: $ i=2 $ .
In the fourth test case, the values $ c_0 $ , $ c_1 $ and $ c_2 $ initially equal to each other, so the array $ a $ already has balanced remainders.
题面翻译【转自洛谷】
本题有 \(t\) 组数据。
有一个长度为 \(n\) 的非负整数序列 \(a_1,a_2,...,a_n\)。
每次操作你可以选择一个元素并将其加 \(1\),问最少需要多少次操作,可以使得序列中对 \(3\) 取模分别等于 \(0\)、\(1\)、\(2\) 的元素个数相等。
保证 \(t \le 10^4\),\(n\) 是 \(3\) 的正整数倍,\(3 \le n \le 3 \times 10^4\),\(\sum n \le 1.5 \times 10^5\),\(0 \le a_i \le 100\)。
翻译提供:HoshizoraZ
思路
模拟,可以每次找出c0,c1,c2的最大值,
如果c0最大,c0--,则如果x%30,x++,那么c1++
如果c1最大,c1--,则如果x%31,x--,那么c2++
如果c2最大,c2--,则如果x%3==2,x--,那么c0++
代码
#include <iostream>
#include <cstring>
#include <cstdio>
#include <cmath>
#include <algorithm>
using namespace std;
const int N = 3*1e4+10;
int a[N];
void solve()
{
int n;
cin >> n;
int x = 0,y = 0, z = 0;
memset(a,0,sizeof a);
for(int i = 0;i < n;i ++)
{
cin >> a[i];
if(a[i] % 3 == 0) x ++;
else if(a[i] % 3 == 1) y ++;
else z ++;
}
int ans = 0;
while(x != y || y != z || x != z)
{
ans ++ ;
if(x >= y && x >= z)
{
x --;
y ++;
}
else if(y >= x && y >= z)
{
y --;
z ++;
}
else if(z >= x && z >= y)
{
z --;
x ++;
}
}
cout << ans << endl;
return ;
}
int main()
{
int T;
cin >> T;
while(T --)
solve();
return 0;
}

 A.Arena
B.方程的解
C.Cat Cycle
I. 掎角之势
K.砝码称重
D.Dense Array
E. Balanced Remainders【补】
A.Arena
B.方程的解
C.Cat Cycle
I. 掎角之势
K.砝码称重
D.Dense Array
E. Balanced Remainders【补】

 浙公网安备 33010602011771号
浙公网安备 33010602011771号