2025-11-25 ZYZ28-NOIP模拟赛-Round9 hetao1733837的record
2025-11-25 ZYZ28-NOIP模拟赛-Round9 hetao1733837的record
比赛链接:ZYZ28-NOIP模拟赛-Round9
A.colorful
提交链接:09-A
题面
题目描述
小 Z 最近收到了一个花花绿绿的矩阵,有 $n$ 行 $m$ 列,位置在第 $i$ 行第 $j$ 列的方格颜色是 $c_{i,j}$。 小 Z 觉得一个矩阵是五彩斑斓的,当且仅当这个矩阵四个顶点上的颜色不都相同。
- 不都相同的意思是,当且仅当矩阵四个顶点上的 $c_{i,j}$ 至少有一个和其他点颜色不同。 现在小 Z 想让你帮忙数一数,这个矩阵有多少个子矩阵是五彩斑斓的。
- 特殊的,原矩阵也算一种子矩阵。
输入格式
从 colorful.in 文件读入数据。 第一行两个正整数 $n,m$,代表矩阵的大小。 接下来 $n$ 行,每行 $m$ 个整数,第 $i$ 个第 $j$ 个整数 $c_{i,j}$ 代表这个位置的颜色。
输出格式
输出到 colorful.out 文件。 输出一个整数,代表五彩斑斓的子矩阵个数。
分析
HXF 容斥模板题。
正难则反,求出总子矩阵数量$\frac{n\times(n+1)}{2}\times\frac{m\times(m+1)}{2}$,减去四个角都相等的矩阵数量,即为五彩斑斓的矩阵数量。
题目要求 $O(n^3)$ 的复杂度,思考如何解决,枚举行,对于两行,枚举列,然后统计颜色相同的即可。
上午一直在烫,多亏机房大佬 AeeE5x 出手相救,直接拿下。
可见,HXF 容斥的思想是即为广泛的,应更加深刻地理解。
正解
#include <bits/stdc++.h>
#define int long long
using namespace std;
const int N = 405, M = 1000005;
int n, m;
int c[N][N];
int buc[M];
signed main(){
freopen("colorful.in", "r", stdin);
freopen("colorful.out", "w", stdout);
ios::sync_with_stdio(0);
cin.tie(0);
cout.tie(0);
cin >> n >> m;
for (int i = 1; i <= n; i++){
for (int j = 1; j <= m; j++){
cin >> c[i][j];
}
}
int ans = (n * (n + 1) / 2) * (m * (m + 1) / 2);
int cnt = 0;
for (int i = 1; i <= n; i++){
for (int j = i; j <= n; j++){
for (int k = 1; k <= m; k++){
if (c[i][k] == c[j][k]){
buc[c[i][k]]++;
ans -= buc[c[i][k]];
}
}
for (int k = 1; k <= m; k++){
if (c[i][k] == c[j][k]){
buc[c[i][k]] = 0;
}
}
}
}
cout << ans;
}
B.travel
提交链接:09-B
题面
题目描述
小 Z 终于迎来了自己的大学生活最后的时刻,他决定用自己的积蓄来一场洗走就走的毕业旅行,并且不玩的开心不上班。然而,他很快就发现这个决定并非那么简单。由于是暑假,假期人多,他既不想错过旅行的最佳时期,又不想在人群中挣扎,预测旅游热门城市的拥挤时段,就像是一道难题摆在他的面前。
在浏览了一堆旅游网站和社交媒体后,小 Z 发现了一个可以帮助他制定完美旅行计划的手机应用程序。这个应用程序基于人工智能算法,预测了旅游热门城市在不同时间的拥挤程度,为旅行者提供了精准的建议。
小 Z 选出来想要旅行的 $n$ 个城市(城市编号为 $1 \sim n$),由于现在交通非常发达,可以认为这些城市之间互相都可以连通,小 Z 每天只会在一个不拥挤的城市停留,第二天他可以选择去任意一个不拥挤的城市并一整天留在那里(当然,也可以继续留在原本的城市,如果原本的城市不拥挤的话),然后他选择这 $n$ 个城市,出发日期 $S$ 和返回日期 $T$(可以理解为小 Z 的旅游日期为第 $[S, T]$ 天),应用程序根据这些信息,开始生成一份详细的报告,其中包括了 $m$ 条信息,每条信息包含三个数 $x$, $l$, $r$, 在第 $[l, r]$ 天是小 Z 选出来的第 $x$ 个城市是拥挤的,通过这份报告,小 Z 了解到了不同城市的拥挤时段,并制定了避开高峰期的旅行计划。有了这个应用程序的帮助,小 Z 可以尝试制定一份完美的旅行计划,开启了一场避开人群的毕业旅行。
由于小 Z 非常懒,不逛完所有城市也无所谓,现在小 Z 想知道他能够实现错峰毕业旅行的方案有多少种(注意小 Z 可以从任意一个城市开始毕业旅行,我们认为两个方案是不同的当且仅当至少存在一天两个方案所处的城市不同,由于这个方案数很大,他只想知道方案数对 $10^9+7$ 取模以后的结果。
输入格式
从 travel.in 文件读入数据。
第一行输入的四个整数 $n$, $m$, $S$, $T$, 含义与上文描述一致。
接下来的 $m$ 行分别包含三个数字 $x$, $l$, $r$, 表示第 $x$ 个城市在第 $[l, r]$ 天是拥挤的,其中 $1 \leq x \leq n$, $S \leq l, r \leq T$,需要注意的是不同信息的 $x$ 可能会相同,但拥挤的时间段 $[l, r]$ 不会与之前给出的 $x$ 城市的拥挤时间有交集。
输出格式
输出到 travel.out 文件。
一行,一个整数,表示小 Z 错峰毕业旅行的方案数对 $10^9+7$ 取模以后的结果。
分析
hyw!稍微卡一下空间暴力差分做法得分 63+,谁造的数据,我***!
然后其实离散化(我也想到了)一下,差分就过了?机房里有人这么说。何意味?NOIP 模拟赛我能拿 200?假的,其实 100 都困难。
那么,我们he一下同学的代码吧!
正解
#include <bits/stdc++.h>
#define int long long
#define mod 1000000007
using namespace std;
const int N = 1000005;
int n, m, s, t;
struct node{
int x, l, r;
}inp[N];
int cnt[N << 2], cha[N << 2], ans = 1;
vector<int> buc;
int qpow(int a, int b){
int res = 1;
while (b){
if (b & 1)
res = res * a % mod;
a = a * a % mod;
b >>= 1;
}
return res;
}
signed main(){
freopen("travel.in", "r", stdin);
freopen("travel.out", "w", stdout);
cin >> n >> m >> s >> t;
buc.push_back(-1);
for (int i = 1; i <= m; i++){
cin >> inp[i].x >> inp[i].l >> inp[i].r;
inp[i].l = inp[i].l - s + 1;
inp[i].r = inp[i].r - s + 2;
buc.push_back(inp[i].l);
buc.push_back(inp[i].r);
}
buc.push_back(t - s + 2);
buc.push_back(1);
sort(buc.begin() + 1, buc.end());
auto it = unique(buc.begin(), buc.end());
buc.erase(it, buc.end());
int M = buc.size();
for (int i = 1; i < M - 1; i++){
cnt[i] = buc[i + 1] - buc[i];
}
for (int i = 1; i <= m; i++){
inp[i].l = lower_bound(buc.begin(), buc.end(), inp[i].l) - buc.begin();
inp[i].r = lower_bound(buc.begin(), buc.end(), inp[i].r) - buc.begin();
}
int day = lower_bound(buc.begin(), buc.end(), t - s + 2) - buc.begin();
cha[1] = n;
for (int i = 1; i <= m; i++){
cha[inp[i].l]--;
cha[inp[i].r]++;
}
for (int i = 1; i <= day - 1; i++){
cha[i] += cha[i - 1];
if (cha[i] < 0)
cha[i] = 0;
}
for (int i = 1; i <= day - 1; i++){
ans = ans * qpow(cha[i], cnt[i]) % mod;
}
cout << ans % mod;
return 0;
}
C.segment
提交链接:09-C
题面
题目描述
小 Z 有一棵线段树。
啥是线段树呢?你可以想象成,一开始,你有一个区间 $[1, n]$,然后,你可以取中点 $x = \frac{1+n}{2}$,把它划分成两个区间 $[1, x]$, $[x + 1, n]$。(之前那个区间 $[1, n]$ 也还在的哦)
然后,你可以继续划分下去,直到把每一个区间都划分成长度为 1 为止,下图就是一棵线段树,维护了区间 $[1, 10]$ 的信息。

假设线段树上,每个节点都存储了它表示的区间内所有元素的信息(比如区间的和)。
那么,当我想知道一个区间 $[l, r]$ 的信息的时候,我一定可以在线段树上找到一些区间,这些区间互相没有交集,且并起来刚好是区间 $[l, r]$。
比如,我在上图的线段树中,要查询 $[4, 8]$ 的信息,那么我找到 $[4, 5]$, $[6, 8]$ 两个区间,就可以表示区间 $[4, 8]$ 的信息了。(把 $[6, 8]$ 替代成 $[6, 7]$, $[8, 8]$ 显然也是合法的策略,但是这样选择的区间更多了,不够优秀)。
我们称,对于一次查询 $[l, r]$,我们需要用到的区间个数为 $f_{l,r}$。比如上图中 $f_{4,8} = 2$, $f_{1,6} = 2$。
我们的问题是:给定线段树根节点所表示的区间范围是 $[1, n]$,以及有 $m$ 次查询,第 $i$ 次查询是 $[l_i, r_i]$,假设你可以在最初时候自由的选择区间分割的位置(每一层的区间划分都可以自由选择,而非只能自由选择划分 $[1, n]$),$\sum_{i=1}^{m} f_{l_i,r_i}$ 最小是多少?
输入格式
从 segment.in 文件读入数据。
第一行输入 $n$, $q$。
接下来 $q$ 行,每行两个数字 $l_i$, $r_i$。
输出格式
输出到 segment.out 文件。
一个数字表示答案。
分析
感觉这题就很好。因为我不会
所以,我要去看题解了。
30pts
对于30分的做法,显然我场上想到了,但是没能实现出来。就是说我们暴力枚举断点,共$2^n$种情况,然后正着判似乎不太能接受,那我就倒着进行区间合并,$dp_n=\sum dp_l\times dp_{n-1-l}$,很经典的卡特兰数。
呃,就这?我们看一下代码。
#include <bits/stdc++.h>
#define int long long
using namespace std;
const int N = 100005;
int n, m;
struct node{
int l, r;
}q[N];
bool vis[N];
int dfs(int l, int r){
int ans1 = 0;
vector<int> stk;
for (int i = 1; i <= m; i++){
if (vis[i])
continue;
if (q[i].l <= l && r <= q[i].r){
++ans1;
vis[i] = 1;
stk.push_back(i);
}
}
int ans2 = 0;
for (int i = l; i < r; i++){
if (ans2 == 0)
ans2 = dfs(l, i) + dfs(i + 1, r);
else
ans2 = min(ans2, dfs(l, i) + dfs(i + 1, r));
}
for (auto i : stk){
vis[i] = 0;
}
return ans1 + ans2;
}
signed main(){
freopen("segment.in", "r", stdin);
freopen("segment.out", "w", stdout);
ios::sync_with_stdio(0);
cin.tie(0);
cout.tie(0);
cin >> n >> m;
for (int i = 1; i <= m; i++){
cin >> q[i].l >> q[i].r;
}
cout << dfs(1, n);
}
甚至可以随机化断点!
#include <bits/stdc++.h>
using namespace std;
mt19937 rnd(time(NULL));
const int N = 1000005, M = 100005;
int n, m, ans, res = 0x3f3f3f3f, l[M], r[M];
long long tmp;
struct node{
int l, r, data;
}tr[N];
void build(int p, int l, int r){
if (p >= N)
return ;
tr[p].l = l;
tr[p].r = r;
if (l == r){
return ;
}
int tmp = rnd() % 511 + 1;
int mid = (l * tmp + r * (512 - tmp)) >> 9;
build(p << 1, l, mid);
build(p << 1 | 1, mid + 1, r);
}
void query(int p, int l, int r){
if (p >= N)
return ;
if (l <= tr[p].l && tr[p].r <= r){
ans++;
return ;
}
int mid = tr[p << 1].r;
if (l <= mid)
query(p << 1, l, r);
if (r > mid)
query(p << 1 | 1, l, r);
return ;
}
int main(){
freopen("segment.in", "r", stdin);
freopen("segment.out", "w", stdout);
cin >> n >> m;
for (int i = 1; i <= m; i++)
cin >> l[i] >> r[i];
for (int i = 1; i <= 100000; i++){
ans = 0;
build(1, 1, n);
for (int i = 1; i <= m; i++)
query(1, l[i], r[i]);
res = min(res, ans);
}
cout << res;
}
100pts
从数据范围 $n \le 500$ 入手,发现可以区间 DP。考虑对于一段区间 $[l,r]$,枚举其断点 $k$,当且仅当另一个区间与 $[l,r]$ 有交集而不包含,切跨过了 $k$,产生贡献。整出神秘前缀和状物加速,没了。
这么简单?看代码!
#include <bits/stdc++.h>
using namespace std;
const int N = 505;
int n, Q, w[N], num[N][N], l, r;
long long dp[N][N];
int main(){
freopen("segment.in", "r", stdin);
freopen("segment.out", "w", stdout);
cin >> n >> Q;
for (int i = 1; i <= Q; i++){
cin >> l >> r;
num[l][r]++;
w[l]++;
w[r]--;
}
for (int i = 1; i <= n; i++){
w[i] += w[i - 1];
}
for (int len = n - 1; len >= 1; len--){
for (int l = 1; l + len - 1 <= n; l++){
int r = l + len - 1;
num[l][r] = num[l][r] + num[l - 1][r] + num[l][r + 1] - num[l - 1][r + 1];
}
}
for (int len = 2; len <= n; len++){
for (int l = 1; l + len - 1 <= n; l++){
int r = l + len - 1;
dp[l][r] = 0x3f3f3f3f3f3f3f3f;
for (int k = l; k < r; k++){
dp[l][r] = min(dp[l][r], dp[l][k] + dp[k + 1][r] + (w[k] - num[l][r]));
}
}
}
cout << dp[1][n] + Q;
}
这么短/jy
还有神秘树状数组写法,有点6了。
#include <bits/stdc++.h>
using namespace std;
const int N = 505, M = 100005;
vector<int> pos[M];
int c[N], f[N][N], sum[N][N], n, m;
void add(int x, int v){
for (int i = x; i < N; i += i & (-i))
c[i] += v;
}
int query(int x){
int res = 0;
for (int i = x; i; i -= i & (-i))
res += c[i];
return res;
}
int dfs(int l, int r){
if (f[l][r] != -1)
return f[l][r];
int cnt = sum[l][r];
if (l == r){
f[l][r] = cnt;
return f[l][r];
}
int minn = 0x3f3f3f3f;
for (int k = l; k < r; k++){
minn = min(minn, dfs(l, k) + dfs(k + 1, r) - cnt);
}
f[l][r] = minn;
return minn;
}
int main(){
freopen("segment.in", "r", stdin);
freopen("segment.out", "w", stdout);
ios::sync_with_stdio(0);
cin.tie(0);
cout.tie(0);
memset(f, -1, sizeof(f));
cin >> n >> m;
for (int i = 1; i <= m; i++){
int x, y;
cin >> x >> y;
pos[x].push_back(y);
}
for (int i = 1; i <= n; i++){
for (auto v : pos[i])
add(v, 1);
for (int j = 1; j <= n; j++)
sum[i][j] = query(n) - query(j - 1);
}
cout << dfs(1, n);
}
D.experioment
提交链接:09-D
原题链接:LG13004 [GCJ 2022 Finals] Schrödinger and Pavlov
分析
5pts
暴力枚举 $2^k$ 种情况。
#include <bits/stdc++.h>
#define mod 1000000007
using namespace std;
int T, n, ans;
char opt[] = {'0', 'C', '.'};
int b[5005];
string s;
bool solve(){
string t = s;
for (int i = 0; i < n; i++){
if (t[i] == 'C'){
if (t[b[i] - 1] == '.'){
t[b[i] - 1] = 'C';
t[i] = '.';
}
}
}
if (t[n - 1] == 'C')
return true;
return false;
}
void dfs(int p){
if (p >= n){
if (solve())
ans = (ans + 1) % mod;
return ;
}
if (s[p] != '?')
dfs(p + 1);
else{
for (int i = 1; i <= 2; i++){
s[p] = opt[i];
p++;
dfs(p);
p--;
s[p] = '?';
}
}
}
int main(){
freopen("experiment.in", "r", stdin);
freopen("experiment.out", "w", stdout);
cin >> T;
while (T--){
cin >> n >> s;
ans = 0;
for (int i = 0; i < n; i++)
cin >> b[i];
dfs(0);
cout << ans % mod << '\n';
}
}
20pts
#include<bits/stdc++.h>
using namespace std;
const int M=1e9+7;
int n;
int to[5007];
inline bool tos(int x,bool f,string s,int p){
if(x==n&&f)return 1;
if(s[x-1]!='C'||p>n)return 0;
return tos(to[x],1,s,p+1);
}int ans=0;
bool now[13];
inline void dfs(int x,string s){
if(x>n){
for(int i=1;i<=n;++i)now[i]=s[i-1];
for(int i=1;i<=n;++i){
if(s[i-1]!='.'){
if(s[to[i]-1]=='.')swap(s[to[i]-1],s[i-1]);
}
}ans=ans+(s[n-1]=='C');
return;
}if(s[x-1]!='?')dfs(x+1,s);
else{
s[x-1]='C';
dfs(x+1,s);
s[x-1]='.';
dfs(x+1,s);
s[x-1]='?';
}
return;
}
int main(){
freopen("experiment.in","r",stdin);
freopen("experiment.out","w",stdout);
ios::sync_with_stdio(0);cin.tie(0);cout.tie(0);
int T;cin>>T;while(T--){
string s;cin>>n>>s;
ans=0;
bool f1=1,f2=1;
for(int i=1;i<=n;++i){
cin>>to[i];
if(to[i]!=i%n+1)f1=0;
if(i!=n&&to[i]<i)f2=0;
}if(f1){
if(s[0]=='.'||s[1]=='.'){
cout<<"0\n";continue;
}s[0]=s[1]='C';
long long ansb=1;
int fa=0;
for(int i=2;i<n-1;++i){
ansb*=1+(s[i]=='?');
if(s[i]!='.')fa=1;
if(ansb>M)ansb-=M;
}if(s[n-1]=='?')ansb+=ansb;
cout<<max(ansb%M,1ll*fa)<<"\n";
continue;
}if(tos(n,0,s,0)){
long long sum=1;
for(int i=0;i<n;++i){
sum*=1+(s[i]=='?');
if(sum>M)sum-=M;
}cout<<sum%M<<"\n";
continue;
}dfs(1,s);
cout<<ans<<"\n";
}
return 0;
}
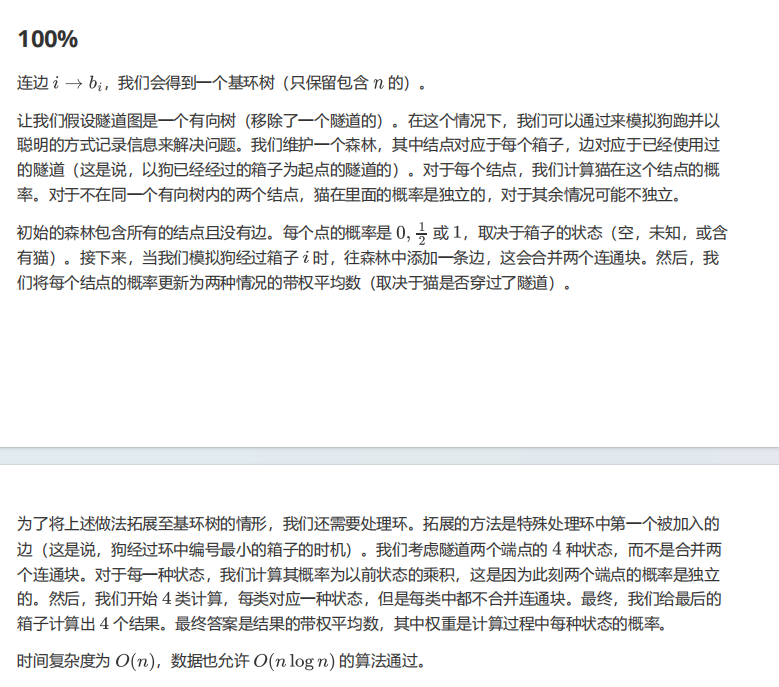
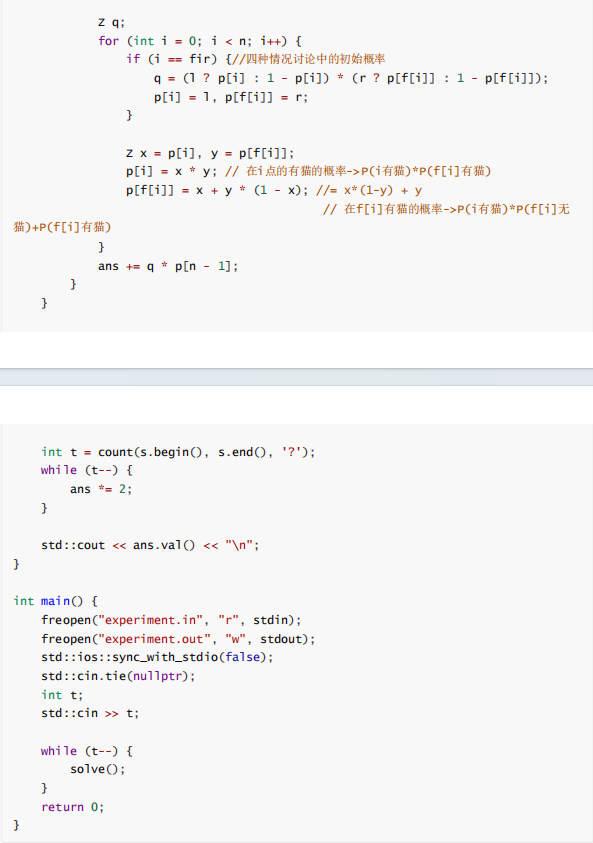
100pts
图一乐吧,不写了。


posted on 2025-11-25 21:20 hetao1733837 阅读(16) 评论(0) 收藏 举报



 浙公网安备 33010602011771号
浙公网安备 33010602011771号