物理着色

第一节介绍最基本的三种反射模型，漫反射，镜面反射和折射

作者：文刀秋二
链接：https://zhuanlan.zhihu.com/p/20091064
来源：知乎
著作权归作者所有。商业转载请联系作者获得授权，非商业转载请注明出处。

表面散射的性质通常用BRDF（双向反射分布函数）来表示。（漫反射）

Lambertian漫反射模型
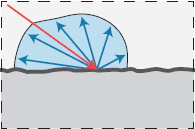
Lambertian很简单粗暴的认为光线被均匀的反射到表面上方的半球中。

均匀的反射出能量，所以返回值是一个常量和出射入射方向无关。
float Lambertian(Vector3 In, Vector3 Out)
{
    // 乘以PI的倒数是因为BRDF在半球内的积分需要为1，满足能量守恒
    return INV_PI;
}

下面是一个用Lambertian材质渲染的图片。

Principled BRDF漫反射模型

Lambertian并不能很好的模拟现实中的许多漫反射材质，现实中完美的均匀反射当然几乎是不存在的，有些现实中的材质会在视线方向接近和表面平行的时候反射更多的光线等。

简单的用两个Fresnel项来增加入射角度低时反射的光线能量强度来模拟这种效果。好处是计算量相对小而且能打到足够的近似。贴一个我自己实现的伪代码，公式在最上面文档的链接5.3章节有，自行查阅。

float DisneyDiffuse(Vector3 In, Vector3 Out)
{
    float oneMinusCosL = 1.0f - AbsCosTheta(In);
    float oneMinusCosLSqr = oneMinusCosL * oneMinusCosL;
    float oneMinusCosV = 1.0f - AbsCosTheta(Out);
    float oneMinusCosVSqr = oneMinusCosV * oneMinusCosV;

    // Roughness是粗糙度，IDotH的意思会在下一篇讲Microfacet模型时提到
    float IDotH = Dot(In, Normalize(In + Out));
    float F_D90 = 0.5f + 2.0f * IDotH * IDotH * Roughness;

    return INV_PI * (1.0f + (F_D90 - 1.0f) * oneMinusCosLSqr * oneMinusCosLSqr * oneMinusCosL) *
		(1.0f + (F_D90 - 1.0f) * oneMinusCosVSqr * oneMinusCosVSqr * oneMinusCosV);
}

下面是用这种漫反射模型渲染的图片。注意球的顶部和Lambertian模型相比，因为入射角度低的缘故，会更加亮，具体量多少也取决于Roughness参数的大小。

下面是一张配上砖块纹理的渲染。

光滑镜面反射。最常见的就是镜子和玻璃一类的材质了，他们分别为导体和电介材质。镜面反射就只是将入射光线根据表面法线反射，并且只在反射方向有能量其他方向均为0。

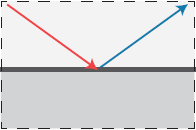
对玻璃这种电介材质则除了反射之外还有根据物体的折射率一部分光线会折射进入物体之中。

反射和折射能量的多少是根据菲涅尔定律决定（Fresnel's Law）。图形学中常常使用用Schlock的近似Fresnel，伪代码如下。

float Fresnel_Schlick(float InCosine, float normalReflectance)
{
        // InCosine是入射光线和法线的夹角，normalReflectance是入射光线和法线垂直时的反射能量大小
	float oneMinusCos = 1.0f - InCosine;
	float oneMinusCosSqr = oneMinusCos * oneMinusCos;
	float fresnel = normalReflectance +
		(1.0f - normalReflectance) * oneMinusCosSqr * oneMinusCosSqr * oneMinusCos;

	return fresnel;
}

值得一提的是在离线渲染，光线追踪里这两种材质本身的着色很容易，只用根据反射和折射的方向射出新的光线然后递归的着色即可。在游戏实时渲染中反射通常是用屏幕空间的反射（Screen Space Reflection）和环境光照贴图两者结合实现的，折射也通常是用扭曲屏幕空间像素的方法。都会有一些Artifact，目前没有完美的解决方案。

贴两张镜面和玻璃材质的渲染。

对于电介材质来说，除了本身的颜色以外，折射率是决定外观的另一个重要因素。折射率决定了折射光线的方向以及全反射的临界角度，上面的图片采用的折射率是1.5，也就是常见的玻璃的折射率，下面这张图则是用折射率2.42的渲染结果，对应的材质是钻石。根据菲涅尔定律，折射率越高的物体反射光线与折射光线的比值也越大，所以整个看起来更加Bling Bling了。读完这篇章至少明白钻石比玻璃更加闪亮，也就够了。

当然现实中不存在完美平滑的表面。接下来提高真实感的一个手段就是对材质表面的法线进行扰动。法线贴图是方法之一。下面是一个镜面反射的物体在表面因为法线贴图变得粗糙之后的模样。

可以看到粗糙的表面更能准确的模拟现实中许多材质的视觉效果。

第二节，基于物理着色（二）- Microfacet材质和多层材质，介绍通过微表面（Microfacet）建模的粗糙表面模型，以及多层次材质的模拟（例如现实中的塑料、陶瓷等，漫反射材质上面有一层透明的镜面图层等）

作者：文刀秋二
链接：https://zhuanlan.zhihu.com/p/20119162
来源：知乎
著作权归作者所有。商业转载请联系作者获得授权，非商业转载请注明出处。

Microfacet（镜面反射）

最常用的Microfacet模型是Cook Torrance。与普通的着色模型的区别在于，普通的着色模型假设着色的区域是一个平滑的表面，表面的方向可以用一个单一的法线向量来定义来定义。而Microfacet模型则认为 1）着色的区域是一个有无数比入射光线覆盖范围更小的微小表面组成的粗糙区域。2）所有这些微小表面都是光滑镜面反射的表面。因为这种模型认为着色区域的表面是由无数方向不同的小表面组成的，所以在Microfacet模型中，着色区域并不能用一个法线向量来表示表面的方向，只能用一个概率分布函数来计算任意方向的微小表面在着色区域中存在的概率。

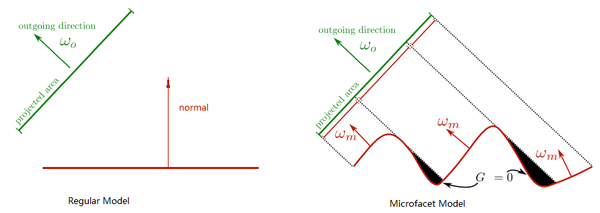
Cook Torrance微表面模型

因为每一个微小表面都做完美镜面反射，上一节提到过完美镜面反射只在入射光和反射光根据发现镜面反射对称的时候才有能量，所以在计算微小表面的BRDF值时，只用先根据入射方向 $w_{o}$ 和出射方向 $w_{i}$ 计算出中间向量 $w_{m}$ 也就是微小表面的法线方向，然后用就可以用法线分布函数计算出这个能够完美镜面反射当前入射和出射光 $D(w_{m})$ 。同样因为是完美镜面反射的缘故，Cook Torrance模型的另一个因素就是菲涅尔（Fresnel）项 $F(w_{o}, w_{m})$ ，这个项和上一节镜面反射BRDF中通到的一样，用于计算不同入射角度的情况下反射的光线的强度，对于导体和电介材质记得使用不同的Fresnel公式。最后，为了更好的模拟着色区域的凹凸不平， $G(w_{o}, w_{i}, w_{m})$ 项则模拟了凹凸表面间的遮挡因素，如上图所示。

BRDF就是 $f(w_{o},w_{i})=\frac{D(w_{m})F(w_{o},w_{m})G(w_{o},w_{i},w_{m})}{4\times cos(w_{o}\cdot w_{n})\times cos(w_{i}\cdot w_{n})}$ ，其中 $w_{m}=\frac{w_{o}+w_{i}}{\left| w_{o}+w_{i} \right| }$

是微小表面的法线，就是入射和出射光线中间的方向， $w_{n}$ 是着色区域实际表面的法线，和普通着色模型中的法线是一样的。

人们也根据这种模型设计出了许多不一样的法线分布函数。大家熟知的Blinn-Phong就是一种很简单的分布函数，相信大家在学最简单的Lighting Shader的时候肯定都看过这段代码

// 计算镜面反射强度
float NdotH = dot(normal, Wm); // Wm = normalize(Wo + Wi)
float specularIntensity = pow(saturate( NdotH ), e);

这就是基于Blinn-Phong的法线分布

$D_{Blinn}(w_{m})=(w_{n}\cdot w_{m})^{e}$ ，其中代表粗糙程度。

Blinn-Phong并不是一个非常真实的分布，上面的公式也并不满足能量守恒定律（需要满足 $w_{m}$ 在半球面上积分为1，Blinn-Phong还需乘以一个常量 $\frac{e+2}{2\pi }$ 才满足这个条件）。近年来有许多新的分布函数被发明出来例如Beckmann，GGX等，他们的能量分布都更接近用光学仪器测量的反射数据。Disney BRDF也使用了GGX分布。本文后面的所有渲染结果也使用了GGX。项也有各种不同的选择，本文使用了有粗糙度作为参数的Smith模型。网上GGX和Smith G项的实现很多，这里就不贴公式了，直接贴两段伪代码。

float GGX_D(Vector3 wm, float alpha) // alpha为粗糙度
{
        float tanTheta2 = TanTheta2(wm),
		cosTheta2 = CosTheta2(wm);

	float root = alpha / (cosTheta2 * (alpha * alpha + tanTheta2));

	return INV_PI * (root * root);
}

float Smith_G(Vector3 wo, Vector3 wi, Vector3 wm, float alpha)
{
	auto SmithG1 = [&](Vector3 v, Vector wm)
	{
		float tanTheta = abs(TanTheta(v));

		if (tanTheta == 0.0f)
			return 1.0f;

		if (Dot(v, wm) * CosTheta(v) <= 0)
			return 0.0f;

		float root = alpha * tanTheta;
		return 2.0f / (1.0f + Sqrt(1.0f + root*root));
	};

	return SmithG1(wo, wm) * SmithG1(wi, wm);
}

粗糙镜面反射

有了Microfacet，我们就可以模拟现实中由非常细小的粗糙表面组成的镜面反射表面了。生活中这种材质很常见，各种粗糙的金属，iPhone6的背面也是：

这种材质将入射光根据表面的粗糙程度分散的反射到镜面反射方向周围的方向，表面越粗糙反射的分布越分散。

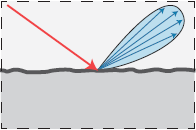
下面的两张渲染结果都是用GGX分布计算的，第二张比第一张更加粗糙（个人觉得第二张很像深空灰iPhone6）。

粗糙镜面折射

Microfacet模型同样可以用于模拟粗糙的折射表面。顾名思义这一种材质则会将入射光线同时反射和折射到镜面反射和折射周围的方向，分布大小取决于表面的粗糙程度。

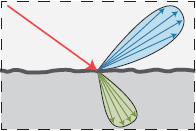
这种材质在现实中的例子就是各种毛玻璃：

折射光线能量的计算相比反射的略微复杂，想了解详细和看推倒过程的可以读这篇Paper：Microfacet Models for Refraction through Rough Surface。

在BRDF计算的时候先要根据入射的方向决定当前发生的是反射还是折射，然后用不同的方法算出两种情况下的 $w_{m}$ ，然后再用反射或者折射的Microfacet公式计算出结果。简单写一下这个过程的伪代码：

float f(Vector3 wo, Vector3 wi, Vector3 wn)
{
	bool IsReflection = true;
	// 根据出入射方向和法线方向判定是反射还是折射
	if(Dot(wo, wn) * Dot(wi, wn) < 0.0f)
		IsReflection = false;

	Vector3 wm;
	if(IsReflection)
		wm = Normalize(wo + wi);
	else // 如果是折射则根据折射率算出wm
		wm = -Normalize(etai * wo + etat * wi);

	float D = GGX_D(wm, Roughness);
	float F = Fresnel(Dot(wo, wm), etai, etat);
	float G = GGX_G(wo, wi, wm, Roughness);

	// 有力D，F和G就可以套入Microfacet的公式计算当前BRDF的返回值。
}

下面贴上用GGX分布计算的粗糙折射的结果。注意在这个Shader Ball的模型的表面下方故意放置了一个Bar，可以看到他因为表面粗糙的关系而被模糊了。第二个比第一个更为粗糙。

当然想真正渲染出更有趣更真实的图片还是少不了Artists给你提供好的Roughness map和法线图。本篇文章的封面就是用Microfacet的粗糙折射材质配合好看的Roughness map渲染的。

写到这里，已经介绍过了漫反射，完美镜面反射和折射，以及基于Microfacet的粗糙反射和折射。然而只有这些还不足以模拟现实中的许多材质。下面介绍另一类很重要的材质，多层材质。

多层材质（Multi-Layered Material）

现实中其实绝大多数的材质都有超过一层以上的组成部分，例如木地板。木头本身是粗糙的漫反射表面，但是木地板都会在表面涂上一层镜面反射的透明油漆。这一类的材质比比皆是，塑料，大理石，瓷器等等。而且严格来说许多漫反射的材质都有些许的镜面反射组成部分在里面。这大概也是当年最早的固定管线渲染可以让你设置镜面光和漫反射光的颜色，渲染的结果就像塑料一样的原因吧。

所以想要渲染出上图一样的材质，就也一定要在构建材质模型的时候考虑多层的信息。幸运的是，我们现在手上已经有之前介绍过的材质作为我们的building block。光是漫反射的表面上增加一层透明的镜面图层（可以是粗糙也可以是平滑）就可以模拟出许多新的材质了！光线传递示意图如下。

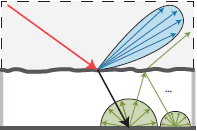
对于以上这种多层次的材质，如果不考虑层次间的反射和折射的话（通常这一部分对视觉的影响也非常小），直接将Microfacet和漫反射的部分相加就可以得到非常不错的效果。

$f(w_{o},w_{i})=f_{diffuse}(w_{o},w_{i})+\frac{D(w_{m})F(w_{o},w_{m})G(w_{o},w_{i},w_{m})}{4\times cos(w_{o}\cdot w_{n})\times cos(w_{i}\cdot w_{n})}$

镜面反射和漫反射的能量的权重需要用电介材质的菲涅尔项进行计算。如果要更加精确的计算不同材质间内部的反射，吸收，以及考虑材质厚度的影响，推荐阅读这一篇论文：Arbitrarily Layered Micro-Facet Surfaces

下面是直接将漫反射项和Microfacet项用Fresnel权重相加得到的表面涂有清漆的木材渲染结果。

这是表面的清漆不那么光滑的渲染结果。

有了这种模型，就已经可以模拟很大一部分现实中的材质了。但是还有相当一部分的材质，一层漫反射加上一层镜面反射是不足以模拟的，一个非常常见的例子就是车漆。通常车漆是在一层粗糙的金属材质外层涂上一层平滑的透明清漆，所以看起来才有下图的样子，首先有金属的质感，但是同时表面又有非常细致的镜面反射。

这一类材质的光线传递示意图如下：

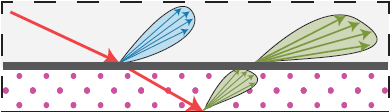
所以对于这种材质来说则需要多次用Fresnel项去叠加两个Microfacet镜面反射。就可以渲染出下图中的材质。

可采样性（Being Samplable）

最后再补充一点，一个材质模型除了需要能计算出特定入射和出射方向的反射的能量大小，还必须是可采样的。可采样意味着要能够给定一个入射方向的时候，重要性采样（Importance Sampling）散射之后的出射方向，以及告诉你当前被采样到的出射方向的概率密度是多少。这是Physically Based Shading非常重要的一点，因为所有的渲染算法都依赖于在材质表面进行散射构造光线传递的路径。所以本文提到的所有材质模型在被设计的时候都是可以进行Analytical的采样的。采样出射光线也被虚幻引擎4在Prefilter环境贴图的时候用到了，这也是虚幻引擎使用Physically Based Shading的好处之一。当然如果有一天游戏想用光线追踪的话，所有的材质都必须要满足可采样性才可以。所以基于物理着色的大趋势还是很好的。

第三节，基于物理着色（三）- Disney和UE4的实现则是在以上的基础上谈谈Disney Principled BRDF的设计思路，参数意义，以及一些漂亮的渲染结果。

作者：文刀秋二
链接：https://zhuanlan.zhihu.com/p/20122884
来源：知乎
著作权归作者所有。商业转载请联系作者获得授权，非商业转载请注明出处。

首先没听过Disney这个Principled BRDF的请戳这个链接（https://disney-animation.s3.amazonaws.com/library/s2012_pbs_disney_brdf_notes_v2.pdf）。从使用率上来说，Pixar的RenderMan，Disney的Hyperion以及UE4都采用了这个模型，说明肯定有值得学习的地方。在这里先谈谈它的设计思路和特点。

直观（Intuitive）

Disney BRDF的最大的特点就是直观。它就像一个万能的Shader可以随便通过调整参数就渲染大部分常见的材质。Artist不需要抓耳挠腮的站在工程师的角度考虑当前的材质有几层，是什么材料的，该选择什么反射模型。相反的，所有参数都直接和最终的视觉结果直接相关，直接根据视觉结果调整不需要真正了解材质的物理性质，而且也更加直观。例如下图，要增加镜面反射，只是增加一个数字就可以了，不需要考虑当前是什么BRDF，有没有使用Microfacet，材质有几层等，当然底层实现还是基于这些前两节说过的模型，只不过这些复杂的模型并没有，也不需要暴露给Artists。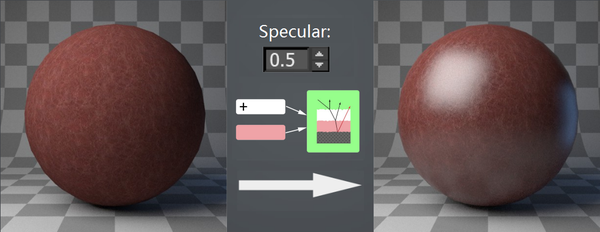

基于外观（Appearance Based）

这一条主要是说参数的定义并不是基于物理性质，或者材质模型的性质，而是基于最终的外观。这样的好处当然是再一次使得系统更加直观易用。Artists可以直接根据参数参数直观的调出想要的某种外观去模拟目标材质。

易于插值（interpolatable）

参数调整时外观改变过度非常平滑，两组完全不同的参数之间直接插值外观的渐变也非常直观。下图是原文从一块橡皮插值到一个金属的过程:

这一点对于使得调整材质时的体验一致性很强，对于易用性甚至培养使用者的习惯都很重要。

基于数据（Data Driven）

所有的参数以及最终材质的外观都是基于MERL BRDF数据库中的数据的。这个数据库储存了100种用光学仪器测量出来的不同材质的双向反射分布函数的值。所有参数是根据这个数据库中存在的材质特性去定制的，而最终参数的结果也会尽量的去匹配这个数据库中的材质外观。所以基于物理什么的在这种直接和最终现实中的数据的方法比起来也显得浮云了。

实现

上面把这个Disney的Shader吹的神乎其神，接下来简单的介绍一下它底层的材质模型到底是长的什么样。它的BRDF用公式表示的话就是这样的：

$f(w_{o},w_{i})=f_{diffuse}(w_{o},w_{i})+f_{subsurface}(w_{o},w_{i})+f_{sheen}(w_{o},w_{i})+\frac{D(w_{m})F(w_{o},w_{m})G(w_{o},w_{i},w_{m})}{4\times cos(w_{o}\cdot w_{n})\times cos(w_{i}\cdot w_{n})}+\frac{D_{2}(w_{m})F_{2}(w_{o},w_{m})G_{2}(w_{o},w_{i},w_{m})}{4\times cos(w_{o}\cdot w_{n})\times cos(w_{i}\cdot w_{n})}$ （3个漫反射+2个镜面反射）

对就是这么简单，和上一节介绍过的有两层镜面反射的材质大同小异，只不过在多了两个subsurface项和sheen项。通过调节给出的参数可以改变每个项的权重，改变Microfacet的分布函数的粗糙参数以及菲涅尔的种类，从而覆盖了非常大范围的材质。Disney BRDF的参数除了最基本的baseColor决定材质的颜色以外，还包括以下几个，所有参数的范围都是0到1：

具体的参数的意义，文档已经讲的很清楚了，我就挑重点的谈谈。个人认为最重要的参数应该是Metallic，Roughness和Specular。下面这张图片是用Metallic 0, Roughness 0.02和Specular 0.5渲染得到的，下面用这个结果作为参考说明其他几个参数对最终外观的影响。

Metallic就是一个插值因子，Metallic为0的时候对应的材质就是一层漫反射材质外面包裹了一层清漆（Clear coat）那种材质，而Metallic为1的时候，则没有任何漫反射项，并且Fresnel项使用导体的（或者直接让Fresnel等于1如果不在乎小细节），在0和1之间的时候则让漫反射项和Fresnel项插值。下面这张图片则是把参考图片的Metallic调成1得到的结果。

Roughness也许则同时影响漫反射项和基于Microfacet的镜面反射项。漫反射项的实现在文章第一节中已经给出了，Roughness越大的时候在入射角低的时候漫反射项会有更强的反光，详见基于物理着色（一）。Roughness的平方则是直接作为Microfacet的分布函数中的粗糙度参数 $\alpha$ 。使用平方的话最终视觉外观的粗糙度更为线性。Microfacet的分布函数中的粗糙度参数 $\alpha$ 则为 $0.5+(0.5\times roughness)$ ，原因是如此出来的结果更符合MERL数据库中的结果。对Roughness的重新映射也体现了之前提到的基于外观和数据驱动的特点。下面这张图片则是把参考图片的Roughness调到0.2得到的结果。

Specular则决定了物体镜面反射强度的大小，实现更是简单不过，0-1就只是映射到Fresnel项中垂直入射角度镜面反射的强度而已。映射的范围是[0-0.08] ,分别对应的折射率范围是[1.0-1.8]，可以覆盖绝大多数的材质。Specular 0.5的时候对应的折射率是1.5，也就是最常见的玻璃材质。下面这张图片是把参考图片的Specular调到0的结果。

Subsurface和Sheen参数文章中并没有给出完整的定义，Disney BRDF中的Subsurface并不是真正的计算完整的次表面散射模型，它只是非常hacky的将diffuse光照到更多原本找不到的地方，这个Subsurface只能用于非常近似的渲染场景中的背景或者细小的次表面散射材质，这里学习的价值不是很大。下面是把参考图片的Subsurface调到1.0的渲染效果。

Sheen则是为了模拟某些布料在入射角度低的时候会反射更强的光，实现也是非常Hacky的直接用多一个Fresnel去增强入射角度低的时候的光线。这么做当然也无法完整的模拟布料的反射模型。下面两张图是Sheen分别为0和1时候的对比。

Clearcoat参数则是第二层镜面反射的强度，现实中有许多两层镜面反射的材质，例如文章第二节中提到的车漆，详见基于物理着色（二）- Microfacet材质和多层材质。Clearcoat的0到1映射第二层镜面反射强度0到0.25，第二层镜面反射中项的 $\alpha$ 使用常数0.25。项的 $\alpha$ 则取决于ClearcoatGloss。下面的两张图是Metallic为1，Roughness为0.7，ClearcoatGloss为0.05时，Clearcoat分别为0和1时的对比。

其他所有以Tint结尾的参数则是对应项是否有颜色。例如SpecularTint为0的时候镜面反射的光照就是无色的（所有光线都被反射），为1的时候则变成BRDF的颜色baseColor。

写到这里，再结合前两张对基本材质模型的介绍，希望这个系列的文章已经给出了一个对Disney这个材质系统的大概的认识。无非就是基于对基本的材质模型间的插值，叠加等操作去模拟更复杂的材质。但是参数的选择则是通过非常用心的分析现实中各种材质外观的特性挑出了一些最能决定外观的参数，并且将这些参数重新映射到0-1的范围内，使得使用的时候更加直观，可以插值，并且重映射非常注重和去拟合现实中测量的反射数据。UE4中的材质系统使用的是同一个BRDF，当然有许多简化的地方，例如漫反射项就只是最简单的Lambertian模型。

下面的图片就是完全用Disney BRDF渲染的，加上好看的纹理，法线贴图以及粗糙图之后几乎是可以以假乱真了（点开看大图）

缺点和限制

当然没有什么是完美的，Disney BRDF也不例外。我个人认为它主要有以下几方面的限制。

不支持透明、折射的材质。此类材质的例子详见本系列文章的前两篇。这也许是最明显的限制了。
参数所能覆盖的材质范围还是有局限性，例如Metallic实际上是一个漫反射材质到金属导体材质的插值，理论上我们还可以用前两张介绍过的任意两个材质模型混合插值出更有趣的材质，例如可以混合平滑的电介材质和粗糙的电介材质去模拟冰块这种材质。然而Disney这个框架并没有给你提供自己做这些拓展的余地。
采样效率问题。在Roughness值很低的时候，Microfacet的镜面反射就会非常接近完美的镜面反射了，但此时再继续使用Microfacet模型就会不如直接使用完美镜面反射模型高效，当然这是可以在实现的时候优化的。
次表面散射材质，布料等有Participating Media的材质都是近似的，不能作为主要的渲染这些材质的工具。

第四节，基于物理着色（四）- 次表面散射则简单介绍了次表面散射材质的相关理论以及算法。

作者：文刀秋二
链接：https://zhuanlan.zhihu.com/p/21247702
来源：知乎
著作权归作者所有。商业转载请联系作者获得授权，非商业转载请注明出处。

表面散射是现实中一种非常常见的材质外观，所有有着半透明外观的物体，例如玉石，大理石，蜡烛，可乐，苹果，牛奶（见下图）包括人类的皮肤，等等。现实中这种半透明的材质其实非常普遍，所以如何为它们的外表建立正确的数学模型是照片级别真实感渲染的重要一部分。

下图则是电影《功夫熊猫3》中的一幕，画面中的玉石也是次表面散射材质的典型例子之一。

与此同时，次表面散射现象的模拟也比在前三篇文章里介绍过的一般的表面反射复杂很多，因为要正确的模拟这种现象，光线不止再物体的表面发生散射，而是会先折射到物体内部，然后再物体内部发生若干次散射，直到从物体表面的某一点射出，例如下图中的（b）。所以对于次表面散射性质的材质来说，光线出射的位置和入射的位置是不一样的，而且每一点的亮度取决于物体表面所有其他位置的亮度，物体的形状，厚度等。之前文章里介绍的表面散射都是基于BSDF模型（双向散射分布函数），而BSDF只能用于描述物体表面某一点的散射性质，所以它无法描述像次表面散射这种现象。

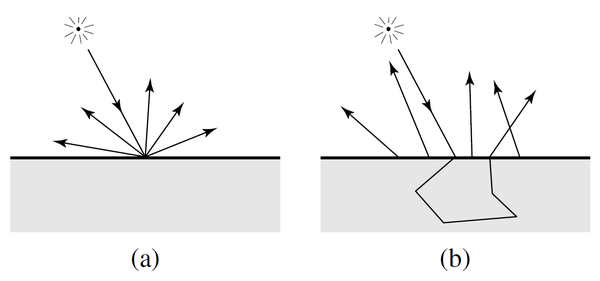
Participating Media（参与介质）

要模拟这样的现象，最简单，最精确，也是计算量最大，最慢的方法，就是直接在物体内部的空间求解带有Participating Media的渲染方程。为了文章的完整性，这里简单介绍一下Participating Media的数学定义，想详细了解可以参考pbrt第11章[1]。

Participlating Media的存在，意味着传统的渲染方程不再是传统的以场景中所有表面为定义域的积分，因为光线在有介质的空间中传播的时候，不用和表面接触，也会被空间中的介质所吸收，散射。通常我们用一下几个参数来描述空间中介质的性质。吸收系数 $\sigma_a$ ，和散射系数 $\sigma_s$ 。前者描述了空间中每单位长度中光子被吸收的概率，后者则描述了每单位长度中光子被散射、既传播方向被改变的概率。散射系数包括了其他方向的光线入射到当然方向的概率，也包括当前方向出射到其他方向的概率。另一个参数是 $\sigma_t=\sigma_a+\sigma_s$ ，就是衰减系数，它是吸收系数和散射系数的和，代表了单位距离内光子出射到其他方向或者被吸收掉的总概率。所以单位距离内辐射度的变化率可以写成：

$\frac{\partial }{\partial t} L_o(p,\omega)=-\sigma_t(p,\omega)L_i(p,-\omega)+\sigma_s(p,\omega)\int_{\delta^2}^{}phase(p,-\omega^{'},\omega)L_i(p,\omega^{'})d\omega^{'}$

第一眼看去貌似有些吓人，实际上说的就是，在介质中，单位长度上Radiance强度的变化会因为被介质吸收而减少，同时一部分能量会随机向外散射出去，最后来自各个其他方向的光线也有一定概率散射到当前方向。其中方程最右边积分中的是phase function，可以理解成空间中的BSDF，定义了空间中一点两个方向间发生散射的概率。另一个值得一提的是，每个频率的光线都有对应的系数。也就是说在用RGB渲染时，每个颜色都要有各自的吸收和散射系数。

这篇文章封面的图片以及下面这张图都是用直接用模拟Participating Media的方法渲染出的玉石。玉石材质是由一个无色的，折射率为1.6的电介材质表面包裹着绿色散射系数较大的均匀介质。由于下图中介质的散射系数要远大于封面中的，所以光线散射的更加频繁，散射间传递的距离更短，导致外观比封面中的玉石更加厚密。

渲染Participating Media的方法有很多，例如最简单的Volumetric Path Tracing，Volumetric Photon Mapping等等。两个参考，[2]是最简单的Volumetric Path Tracing的tutorial，[3]是State of the art的Participating media estimator。因为话题很大，这里不再展开，以后有时间会再专门写写相关的内容。

BSSRDF的定义

模拟次表面散射的另一大类方法就是通过BSSRDF（Bidirectional Surface Scattering Reflectance Distribution Function）对材质建模。和BRDF的不同之处在于，BSSRDF可以指定不同的光线入射位置和出射的位置。Jensen在2001年的论文[4]可以说那是次表面材质建模最重要的一篇论文，推导了许多重要的物理公式，计算模型，渲染时的参数转换，以及测量了许多生活中常见材质的散射系数等等。大部分后来的论文都是在基于这篇文章中的理论的一些提升。不过这篇论文中有大量的数学以及物理公式，对没有一定数学基础和没有接触过材质建模，体渲染的人来说读起来很快就会摸不着头脑。好在大部分公式的意义都在于推导和证明BSSRDF的计算，所以这篇文章会挑出几个和实现次表面散射直接相关的重要公式简单介绍，如果想了解全部细节，还是请参考[4]原文。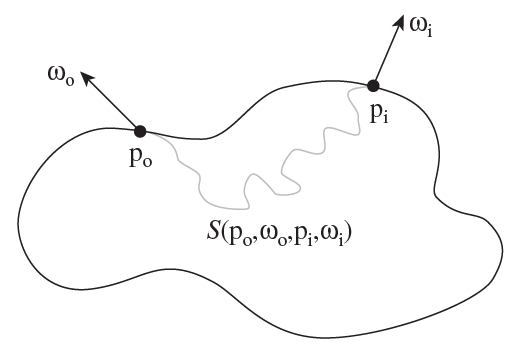

BSSRDF的意义在于快速的近似。对于许多吸收系数特别低，散射系数特别高的材质来说（大部分浑浊的半透明物体例如牛奶，大理石，苹果，肉等等），一束光线会在物体内部散射成千上万次散射，才会彻底被吸收。直接用最暴力的Path Tracing去模拟则意味着每个Sample都需要散射上千次，收敛速度很慢。

对于之前的BRDF来说，一次反射光照的计算是在光线交点的法线半球上的球面积分。而对于BSSRDF来说，每一次反射在物体表面上每一个位置都要做一次半球面积分，是一个嵌套积分。

$L_o(p_o,\omega_o)=\int_{A}^{} \int_{\xi_{(n)}}^{} S(p_o,\omega_o,p_i,\omega_i)L_i(p_i.\omega_i)\left| cos\theta_i \right| d\omega_idA$

其中BSSRDF的定义是：

$S(p_o,\omega_o,p_i,\omega_i)=\frac{1}{\pi}F_t(\eta _o,\omega_o)R_d(\left| {\left| p_i-p_o \right| } \right| )F_t(\eta _i,\omega_i)$

其中包括了光纤入射和出射材质表面时候的折射Fresnel项，一个归一化的 $\frac{1}{\pi}$ 项，和一个diffuse项。除了diffuse项以外，其余的项都非常直观。下面就着重说说这个diffuse项。首先只接受一个标量参数，这个参数的意义是光线入射位置和初设位置的曼哈顿距离。直观的理解就是，BSSRDF尝试将光线在物体表面内部中数千次的散射后所剩余的能量用一个基于入射点和出射点之间距离的函数去近似。

这个近似则是基于几个假设。第一个假设是，次表面散射的物体是一个曲率为零的平面。第二个假设是，这个平面的厚度，大小都是无限。第三个假设是，平面内部的介质参数是均匀的，最后一个假设是光线永远是从垂直的方向入射表面。正因为有这些假设，所以很容易把出射光的强度与出射点和入射点之间的距离用一个函数去近似。下图是用unbiased monte carlo方法模拟的一束光照在平面均匀介质

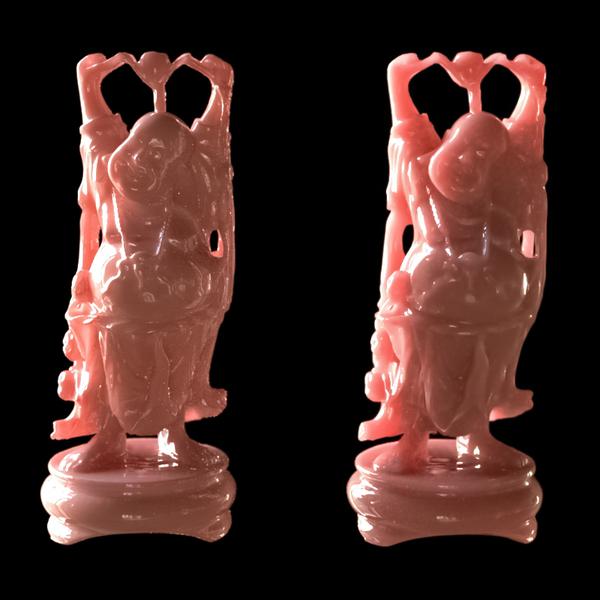
当然实际渲染中这种平面不存在，所有模型都不是无限厚度的，也都是有各种形状的，现实中所有物体内部的散射系数也都肯定不会是均匀的。这也是BSSRDF近似渲染的最主要的错误来源。下图是我在EDXRay里用两种完全不同的方法渲染的颜色，材质以及介质参数完全一样的两个佛像。左边的佛像是基于BSSRDF，右边的则是无偏的Participating Media，两者还是有细微的差别的。BSSRDF因为假设所有表面都的厚度都是无限的，在实际模型中如果有厚度比较薄的地方，误差会更为明显。这也是为什么BSSRDF渲染的结果相比Participating Media要暗淡一些。除了这些误差以外，BSSRDF也没办法渲染出焦散，无法正确的渲染表面以下的几何模型（注意封面shader ball左侧在球内部的写有sub-surface的黑色模型）。

那么究竟的定义是什么呢。理论上来说它需要尽可能的只通过离光线入射点的距离就算出出射点的能量。首先在场景及其简化的情况下，例如一个点光源完全被包围在散射系数均匀的介质中，散射的能量和光源的距离的关系可以用下面的公式算出来。

$\phi(r)=\frac{e^{-\sigma_tr}}{4\pi r^2} +\frac{\sigma_s}{2\pi^2r} \int_{0}^{\infty} \frac{arctan^2u}{u-\alpha arctanu} sin(r\sigma_tu)du$

但是这个积分并没有办法解析的求解，数值方法求得的解也会发散。再加上没有任何公式能直接根据距离准确的计算任何在有限空间内，表面形状任意时候的次表面散射的能量。所以寻求某种近似是必须的。其中一个这些年非常流行的近似算法就是用求解Diffusion方程的方法。

$\phi(r)=\frac{1}{4\pi D} \frac{e^{-r\sqrt{\frac{\sigma_a}{D} } }}{r}$ ,

相比上面的精确解，Diffusion的近似简单了许多，只是一个距离自然指数除以距离。这个方程也是Jensen 2001[4]中Dipole近似的核心。实际上过去的所有次表面散射相关的论文都在不断的提出新的方法来更准确的理解这个方程的性质和提高它的精确度。

然而这篇文章并不想着重介绍Dipole[4]以及其延伸算法例如Multipole[5]，Directional Dipole[6]。所以读到这也不必太在意上面两个眼花缭乱的公式。

Normalized Diffusion

Pixar的Christensen（曾经差点和他成为同事）在去年发表的一篇论文中[7]，试验出了一个函数，它没有基于任何Diffusion或者光线传递的理论，就直接可以比几乎以往所有的算法都能更精确的直接逼近介质渲染方程的正确解。不仅如此，这个方程本身只含有两个指数函数，实现和计算都非常简单。而且它还可以的解析的求Cumulative Distribution Function(CDF)，渲染时要Importance Sampling也非常方便。实际上上面红色的佛像就是用这个方法渲染的。当然它同样也要满足以上提倒的那几个假设。

因为这个函数从0到 $\infty$ 的积分永远是1，所以这个方法的名字叫做Normalized Diffusion。它的定义如下：

$R_d(r)=\frac{e^{-r/d} + e^{-r/3d}}{8\pi dr}$ ，

就是这么简单。其中是一个控制这个函数形状的参数。我们只需要根据不同的介质散射系数计算出适合的，就可以非常准确的逼近Participating Media的无偏解。下图截自[7]，意思就是说上面那个如此简单的公式可以做到比传统的数个复杂许多的算法更精确度逼近基于蒙特卡洛暴力积分的无偏解。A是材质表面的反射率（既RGB值）。注意，原来的Diffusion方法所计算的都只包括了材质中的多重散射（Multiple Scattering），直接散射（Single Scattering）则要单独用Ray Marching的方法求解。而Normalized Diffusion在函数里就默认包含了直接散射，实现和计算上都更加简单。

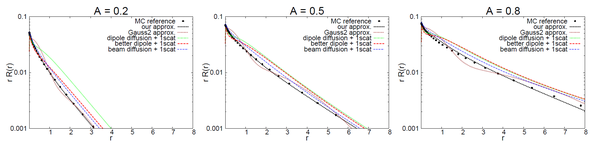
Normalized Diffusion所接受的介质参数和传统的有所不同。通常描述介质用的是吸收系数 $\sigma_a$ ，和散射系数 $\sigma_s$ 。但是由于它们和最终材质外观的联系并不是一个线性关系，下面的表格可以看出 $\sigma_a$ 和 $\sigma_s$ 与材质的颜色的关系非常摸不着头脑。所以Artists并不能很方便的直接调整这些系数。所以其实大部分渲染器都会把这些系数映射成材质表面的Albedo和平均散射距离（diffuse mean free path）供Artists调整。不仅如此，也只有这也，才可以将纹理上的颜色应用到次表面散射材质上去。

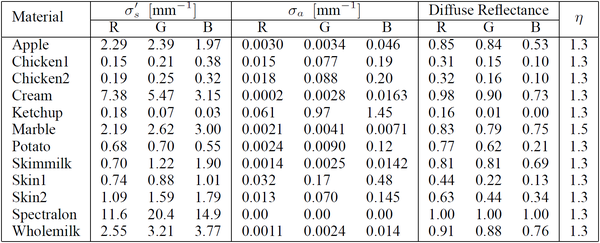从Albedo和平均散射距离到介质系数的映射在[4]中就有介绍。

$DiffuseAlbedo=2\pi\int_{0}^{\infty}R_d(r)rdr=\frac{\alpha^{'}}{2}(1+e^{-\frac{4}{3}A\sqrt{3(1-\alpha^{'})} }) e^{-\sqrt{3(1-\alpha^{'})} }$

其中 $\alpha^{'}$ 是reduced albedo， $\alpha^{'}=\sigma_s^{'}/ \sigma_t{'}$ 。 $\sigma_a^{'}$ 和 $\sigma_s{'}$ 则是散射系数受到phase function影响之后的reduced scattering coefficient。 $\sigma_s{'}=\sigma_s\times (1-g)$ , $\sigma_t^{'}=\sigma_s^{'}+\sigma_a$ 。则和表面的折射率有关， $A=(1+F_{dr})/(1-F_{dr})$ ， $F_{dr}=-\frac{1.44}{\eta^2}+\frac{0.710}{\eta}+0.668+0.0636\eta$ 。

平均散射距离 $l_d\approx 1/\sigma_{tr}$ ，而 $\sigma_t^{'}=\frac{\sigma_{tr}}{\sqrt{3(1-\alpha^{'})} }$ 。

上面那堆公式就足够能解出材质的散射系数。这里可以看出Normalized Diffusion另一个优势是，方程的输入直接就是Diffuse Albedo和平均散射距离，不需要求解上方那些复杂的公式。

值本身的计算，也是通过函数拟合。给定一个材质的反射率，以及介质的平均散射距离，再假定光线是以光束的形式垂直射入物体的话， $d=\frac{l_d}{3.5+100(A-0.33)^4}$ 。想了解其他拟合的计算方法，例如光线是以漫射的形式入射表面等，请参考[7]。

因为这里的积分时永远等于1，所以渲染的时候只要直接乘以材质的Diffuse Albedo就可以了。当平均散射距离为0的时候，会收敛到和漫反射材质一样的结果。下图是五只用Normalized Diffusion渲染的兔子，平均散射距离从左到右由小变大。

BSSRDF重要性采样

利用BSSRDF渲染的方法大致有两种。Jensen在[4]中提出了一种直接在物体的入射点周围根据重要性采样出射点的方法。接着Jensen又在[8]中提出了一种基于点云的方法，先将许多点随机分布在次表面的模型上，然后在每个点预计算irradiance，最后利用这些点云信息快速查找积分。这个算法的优势是速度比前者快两三个数量级，缺点则有额外的内存开销，需要多一个预计算的Pass，实现起来较为麻烦，不适合progressive渲染，同时点云的分布影响渲染质量，容易在animation中出现flickering等等。

所以这里介绍的方法还是基于直接对BSSRDF进行重要性采样。Solid Angle在2013年提出一个多轴投射的采样方法[9]。首先根据在入射点周围的圆盘上根据的分布采样一个距离，接着将这个点垂直投影到模型的表面上。因为BSSRDF是在物体的表面积上积分，所以在遇到和入射点法线方向不同的表面时，样本的pdf需要乘以入射和出射点法线的点积。当入射与出射表面接近垂直的时候，pdf就会非常小。所以[9]中的做法是用一定的概率在binormal和tangent方向进行投影，然后用多重重要性采样计算样本的pdf，就可以在凹凸不平的表面达到更快的收敛速度。

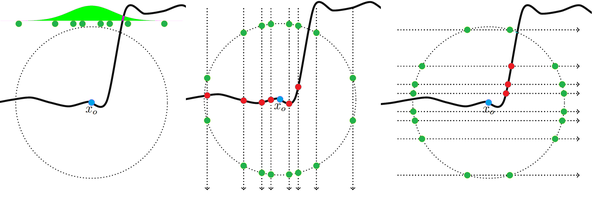
至于对散射距离的采样，Normalized Diffusion的CDF可以直接用下面的公式计算:

$cdf(r)=1-\frac{1}{4}e^{-r/d}-\frac{3}{4} e^{-r/3d}$ .

只不过采样需要的 $cdf^{-1}$ 无法解析的表达，这里可以直接用预计算查表的方法解决。计算的时候让等于1，查表时乘以实际的就能得到散射距离。有了以上采样的方法，就可以把次表面散射采样的路径作为一种特殊路径集成到Path tracing或者Bidirectional path tracing的积分中去。

最后放多几张次表面散射材质的美图。本文中所有渲染结果均使用本人自己开发的渲染器EDXRay。

posted @ 2016-08-20 14:36 何人之名阅读(2864) 评论(0) 收藏举报

刷新页面返回顶部

何人之名

普通男子，胸有大志，昨日可忆，未来可期，有山水可游，有奇事可闻，有朋友可交，有家人可依，文字之乐暂无，童稚之心已灭，完满一生。

物理着色

Participating Media（参与介质）

BSSRDF的定义

Normalized Diffusion

BSSRDF重要性采样

公告