剑指OFFER-入门书籍-《算法图解》

前三章，算法基础：二分查找、大O表示法、基本数据结构（数组和链表）、递归。
剩余：具体问题解决技巧、何时采用贪婪或动态规划，散列表的应用，图算，K最近邻。

算法实际应用

GPS: 图算
国际跳棋AI: 动态规划
推荐系统: K最近邻
游戏开发: 图算

有限时间不可解

概念: NP完全问题, NP不完全问题

二分查找

使用二分查找的前置条件: 有序列表

运行效率: O(logn)

对数运算是幂运算的逆运算, log(10)100=2, log(2)1024=10, log(2)8=3, log100≈7, log10亿≈30 log默认以2为底。

可汗学院有一个不错的讲解对数的视频

基本运行规律:

  1. 查找元素a
  2. low=低位, high=高位
  3. 每次从中间开始检查, mid=(low+high)/2
  4. 如果元素a大于mid位置的元素, low=mid+1, 进入第3步

大O表示法

特点: 指出了最糟糕情况下的运行时间

常见大O运行时间:

  1. O(logn) - 对数时间
  2. O(n) - 线性时间
  3. O(n*logn), 包括快排
  4. O(n²), 包括选择排序
  5. O(n!), 旅行商问题非常慢
  6. O(1) - 常量时间

算法速度指的并非时间，而是操作数的增速，随着输入规模的增加，运行时间将以什么样的速度增加。

拓展：精确化算法耗时

假设线性时间A=O(n)=10msn （假设很简单的操作10ms完成n次）
假设对数时间B=O(logn)=1slogn (假设操作较复杂1s完成logn次)
求A和B的交点，n=100logn, 也就是2的(n/100)次方等于n的问题求解约等于996
那么当小于该交点时(小数据量)时，A更有利，反之B更有利。

const f = (n) => Math.round(Math.pow(2, n/100)) == n) ? n : f(n+1); n取2以上

拓展: 最好情况和最快情况

对于n: 最好为1，最坏为n

  • 最差情况：逆排序数组使用选择排序，为n
  • 最优情况：数组接近排序要的效果，调换个别次序，为1
    对于logn:
  • 最差情况：已排序数组，基准值选端点值，logn将变成n
  • 最优情况：已排序数组，基准值选中间，为logn

也就是说：

  • 非常混沌且大的数组，选logn
  • 几乎接近已排序状态的数组，选n
  • 几遍简单的交换无法解决排序的数组，选logn

旅行商问题

相同性质的问题: 球队比赛问题

问题: 5个城市之间旅行，确保旅程最短

可能的排列方式: 5!=120, 6!=720, 7!=5040

数组和链表

数据访问方式: 随机访问(数组快)、顺序访问(链表相比数组无需整块内存，擅长(插入和删除)

可以区分化的场景:

  • 洗摞成一叠的盘子(链表)
  • 服务员在队尾添菜单厨师在队首取出菜单做菜(链表)
  • 从静态存储的一堆用户名中进行查找(数组)
  • 混合数据存储-链表数组，数组包含26个字母元素，每个元素指向一个字母打头的用户名链表，查的较快、易于修改

选择排序(O(n²)）

复杂度=((n-1) + (n-2) + ... + 1) = n(n-1)/2

问题: 将乱序列表排成有序表

基本运行规律:

  1. 建立一个空数组arr
  2. 从列表中挑最大的放到arr中
  3. 列表长度-1，进行第2步

递归

经典问题: factorial阶乘

基本运行规律:

  1. 给定数n
  2. 给定函数f(n)=n*f(n-1), f(1)=1, n为非零正整数
  3. 计算结果f(n)

const f = (n) => n == 1 ? n : n * f(n-1)

要点：

  1. 基线条件(base case, 如上面的如果 n等于1 返回 1)
  2. 递归条件(recursive case, 如上面的如果 n不等于1 返回 n*f(n-1))

启发问题：将数组求和使用递归实现(函数式编程思想)

  1. 数组arr=[a,b,c]
  2. sum(arr)=arr.pop() + sum(arr)
  3. const sum = (arr) => arr.length == 1 ? arr[0] : arr.pop() + sum(arr)
  4. 基线条件：数组长度不为0

栈

调用栈(洗盘子)基本逻辑：

  1. 先调用函数A，后调用函数B
  2. 函数A内包含函数C
  3. 函数B内包含函数A

调用栈顺序（左边是底，右边是顶）：BACAC

特点：

  1. 像弹夹，只有1个开口，先进去（压入）后出来（弹出），先入后出
  2. 每个函数调用都会占用一定内存
  3. 如果调用栈太长占用大量内存，可以使用尾递归或转为循环优化

快速排序(O(nlogn))

核心思想：分治策略（分而治之，divide and conquer，D&C）

效率：O(nlogn)

和其他方法的关联：使用递归

分治

分治经典问题：均等划分土地(长m宽n)为方块，并且使得方块最大，求格子多大有多少块（切格子, 欧几里得算法、辗转相除法、最大公约数）

基本运行规律：

  1. 找基线条件，求得最小方块格子的前一个格子长边为短边的整数倍（实质就是寻找最大公约数）
  2. 分解问题（缩小规模）
func 最小边(长边m, 短边n) {
  if (m % n == 0) return n
  else {
    m = max(m-n, n)
    n = min(m-n, n)
    return 最小边(m, n)
  }
}

const f = (m, n) => {
  if (m < n) {
    c = m;
    m = n;
    n = c;
  }
  return (m % n == 0) ? n : f(m-n, n)

快排

C语言标准库：qsort

核心：性能高度依赖基准值

基本运行规律：

  1. 给定乱序数组arr
  2. 确定基线条件: 数组为空或只含1个元素(无法再切分)
  3. 确定基准值n(可以是arr[0],arr[mid],arr[arr.length-1])
  4. arr根据基准值分为arr_left(小)和arr_mid(中)和arr_right(大), 分别进行第3步
const f = (arr) => {
   const b = arr.length;
   if (b < 2) return arr; // 基线也可以用位运算 b | 1 === 1
   const index = b % 2 === 0 ? b/2 : (b+1)/2;
   const pivot =  arr[index];
   let arrleft = []; let arrright = []; let arrmid = [pivot];
   for (let i = 0; i < arr.length; i++) {
     if (arr[i] < pivot) arrleft.push(arr[i]);
     else if (arr[i] > pivot) arrright.push(arr[i]);
     // else if (i != index) arrmid.push(arr[i]);
   }
   // 这样有一个副作用，会默认去重
   // 不去重的话在等于时再进行一遍角标判断
   return [...f(arrleft), ...arrmid, ...f(arrright)]
}

合并排序

合并排序相比快速排序，受常量影响的时间大得多，快排遇上平均情况的可能性更大。

散列表

查找时间为O(1)

散列函数，f(x)=y，一个x映射一个y。

散列函数必须满足的基本要求：

  1. 数据一致性。每一个输入对应一个确定的输出。
  2. 不同的输入映射不同的输出。

散列函数的工作原理：

  1. 总将相同的输入映射到相同的索引。
  2. 将不同的输入映射到不同的索引。
  3. 散列函数知道数组有多大，只返回有效的索引。（如数组包含5个元素，散列函数就不会返回无效索引100）

散列函数+数组=散列表（hash table）

数组、链表都直接映射到内存，散列表更复杂，它使用散列函数来确定元素的存储位置。

在复杂数据结构中，散列表（也叫散列映射、映射、字典、关联数组）最有用，速度很快。

  • Python-提供的散列表叫字典（dict()）
  • JavaScript-提供的散列表叫对象（Object.create(null))

实际应用：DNS解析（DSN resolution）、缓存

缓存的两个优点：

  1. 速度更快
  2. 计算更少

总结，散列表适合于：

  1. 模拟映射关系
  2. 防止重复
  3. 缓存/记住数据

散列表本身是无序的，因此添加键-值对的顺序无关紧要。

散列函数核心-防冲突（anti-collision）

简单的散列函数：

  • 字母表顺序分配数组位置
  • 相同首字母的单词存储发上冲突，最简单的解决办法：
    • 如果两个键映射到同一个位置，就在该位置存储一个链表
    • 缺点：性能差，散列表可能分布不均匀，访问链表上的数据时速度变慢（由O(1)变到O(n)，链表越长速度越慢），

理想的情况：散列函数将每个键均匀地映射到散列表的不同位置

散列表的性能：

  • 查找速度（获取给定索引处的值）于数组一样快
  • 插入和删除速度与链表一样快

在最糟情况下，各种速度都很慢，所以需要避开最糟情况（防冲突），它需要：

  1. 较低的填装因子（基线条件：填装因子>0.7，操作：调整散列表长度）
  2. 良好的散列函数

填装因子=散列表包含的元素数/位置总数

填装因子>1意味着元素数量超过数组位置数，一旦填装因子开始增大，就需要在散列表中添加位置，这被称为调整长度（resizing）。

假设填装因子已经相当满（3/4），就需要调整长度，创建一个更长的新数组（通常为1倍），再使用hash函数将所有元素插入到新的散列表中。

启发：

  1. 电池尺寸到功率的映射，其中电池尺寸为A、AA、AAA和AAAA。可将字符串的长度作为索引。
  2. 将每个字符映射到一个素数：a=2，b=3，c=5， d=7，e=11，假如散列表长度为10，字符串bag的索引=(3+2+17)%10=22%10=2。

广度优先搜索（breadth-first search，BFS）

属于图算法。可用于找出两样东西之间的最短距离：

  1. 国际跳棋AI，计算最少步数；
  2. 拼写检查器，计算最少编辑多少个地方可修正错频单词。

在所有算法中，图算法时最有用的。

最短路径问题（shorterst-path problem）。解决最短路径问题的算法是 BFS。

最短路径问题的基本步骤：

  1. 使用图建立问题模型
  2. 使用广度优先搜索解决问题

图的组成元素：节点（node）、边（edge）

图的简单分类：有向图（directed graph）、无向图（undirected graph）

一个节点直接相连的周围节点被称为邻居。

BFS的直接体现：构建人际关系网，一度关系是朋友，二度关系是朋友的朋友，找人帮忙时就会用到BFS。

BFS图的实现

每个节点都与邻居节点相连，类似于一种“你->Bob”的关系映射，散列表可以让你将键映射到值。

graph["you"] = ["alice", "bob", "claire"]

实现算法工作原理：

  1. 创建一个队列，用于存储要检查的人
  2. 从队中弹出一个人
  3. 检查该人是否是需要的人
    4.a 是，完成
    4.b 否，将该人的所有邻居都加入队列
  4. 前往第2步
  5. 队列空，没找到。
graph = {
  'you': ['alice', 'bob', 'claire'],
  'alice': ['billy', 'paro'],
  'bob': ['martin'],
  'claire': ['elon', 'billy'],
  'billy': [],
  'paro': [],
  'martin': [],
  'elon': [],
}

const f = () => {
  search_queue = [];
  search_queue += graph['you'];
  while (search_queue) {
    person = search_queue.shift()
    if (person) return person
    else search_queue += graph[person]
  }
  return null;
}

上面 billy 是 alice 和 claire 的共同朋友，它被检查了两次。
将其标记为已检查且不再检查。否则，假如这里的图关系是 ‘你<->billy’ 可能导致无限循环。

更新算法：

f = () => {
  search_queue = [];
  search_queue += graph['you'];
  searched = [];
  while (search_queue) {
    person = search_queue.shift()
    if (person) return person
    else if(person not in searched) {
      search_queue += graph[person]
      searched.push(person)
    }
  }
  return null;
}

总结：

  1. 必须按加入顺序检查搜索列表中的人，否则找到的就不是最短路径，因此搜索列表必须是队列；
  2. 对于检查过的人，务必不要再检查，否则可能导致无限循环。

BFS效率

沿着每条边前行，运行时间=O(Sum(边))
使用队列，将人添加进队列时间固定 O(1)，对每个人做的总时间=O(Sum(人))

O(BFS)=O(人数+边数)=O(V+E), V=vertice顶点

拓展-拓扑排序

单向进行的图背后的列表是有序的，其中如果任务A依赖于任务B，A就必须在B后面，这种方式被称为“拓扑排序”。

拓扑排序的有用场景，构建一个有序的任务列表：

  1. 规划一场婚礼的所有事情
  2. 创建一个家谱

有向无环加权图最短路径算法——狄克斯特拉算法（Dijkstra's algorithm）

BFS找出的是段数最少(将段数看成“边”)的最短路径。

Dijkstra找出的是时间最少(将时间看成“权重”)最少的最短路径。

注意: BFS注重Min(Sum(边))，Dijkstra注重Min(Sum(权重)), 边最少不代表权重最小，权重最小不代表边最少。

Dijkstra核心：找出图中最便宜的节点，并确保没有到该节点更便宜的路径。

Dijkstra算法步骤:

  1. 找出“最便宜”节点，可在最短时间内到达的节点。
    2.对于该节点的邻居，检查是否有前往它们的更短路径，如果有就更新该节点的邻居开销；
    3.重复1，2直至对图中每个节点操作完毕
    4.计算最终路径。

属于：权重(weight)，加权图(weighted graph)，非加权图(unweighted graph)

无向图意味着两个节点彼此指向对方，其实就是环。

Dijkstra 只使用于有向无环图(directed acyclic graph, DAG)

负向边

如果有负权边，就不能用狄克斯特拉算法。可使用贝尔曼-福德算法（Bellman-Ford algorithm）。

Dijkstra算法实现

解决问题：

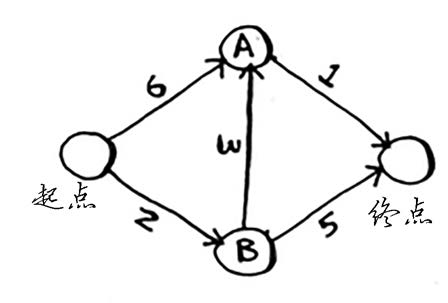
需要三个散列表：Graph、Costs、Parents

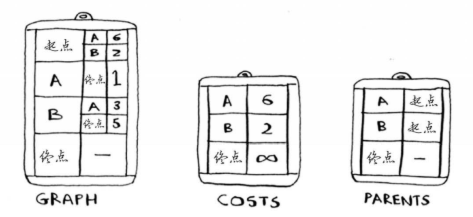
随着算法的进行，将不断更新 costs 和 parents。

graph = {
  'start': {
    'a': 6,
    'b': 2,
  },
  'a': {
    'fin': 1
  },
  'b': {
    a: 3,
    fin: 5,
  },
  'fin': {} // 无任何邻居
}

costs = {
  a: 6,
  b: 2,
  fin: infinity
}

parents = {
  a: start,
  b: start,
  fin: None
}

processed = [] // 用于记录处理过的节点

具体算法步骤：

  1. 只要有要处理的节点，就
  2. 获取离起点最近的节点
  3. 更新其邻居的开销
  4. 如果有邻居的开销被更新，同时更新其父节点
  5. 将该节点标记为处理过，前往第1步
node = find_lowest_cost_node(costs)
while node is not None:
  cost = costs[node]
  neighbors = graph[node];
  for n in neighbors.keys():
    new_cost = cost + neightbors[n]
    if costs[n] > new_cost:
      costs[n] = new_cost;
      parents[n] = node;
  processed.append(node);
  node = find_lowest_cost_node(costs);

find_lowest_cost_node

const f = (costs) => {
  lowest_cost = INFINITY
  lowest_cost_node = None
  for node in costs:
    cost = costs[node]
    if cost < lowestcost and node not in processed:
      lowest_cost = cost
      lowest_cost_node = node
  return lowest_cost_node
}

总结：

  1. 图，用于解决最短路径问题。
  2. BFS用于非加权图；
  3. 狄克斯特拉用于权重为正的加权图；
  4. 贝尔曼-福德用于包含权重为负的加权图；

贪婪算法

贪婪策略 - 非常简单的问题解决策略：每一步都选择局部最优解。

适合解决的问题：

  1. 调度问题
  2. 部分背包/装箱问题
  3. 旅游价值最大化问题
  4. 集合覆盖问题

集合

水果集合：鳄梨、西红柿、香蕉

蔬菜集合：甜菜、胡萝卜、西红柿

并集：水果和蔬菜

交集：既属于蔬菜又属于水果(西红柿)

差集：属于水果但不属于蔬菜(鳄梨, 香蕉), 属于蔬菜但不属于水果(甜菜, 胡萝卜)

集合的特点：

  1. 集合类似列表，但不包含重复的元素
  2. 集合运算有并、交、差

集合覆盖问题

有时候只需一个能够大致解决问题的算法，此时适合贪婪，实现起来容易其结果又与正确结果接近。

部分问题寻求最优解的时间非常长，此时也适合使用贪婪算法获得一个非常接近的解，如：
集合覆盖问题，找出覆盖50个州的最小广播台集合，具体方法如下：

  1. 列出每个可能的广播集合，称为幂集（power set），可能的子集有2^n个；
  2. 在这些集合中，选出覆盖全美50个州的最小集合。
    运行时间=O(2^n)

使用贪婪算法解决问题，运行时间=O(n^2)。

具体步骤：

  1. 简化问题，假设要覆盖的州没那么多，广播台也没那么多；
  2. 创建一个列表，包含要覆盖的州；
  3. 使用一个集合来存储最终选择的广播台；
  4. 计算
    4.1 选择覆盖最多的未覆盖州的广播台，存进best_station中
states_needed = set(["mat", "wa", "or", "id", "nv", "ut"])

stations = {
  "kone": set(["id", "nv", "ut"]),
  "ktwo": set(["wa", "id", "mt"]),
  "kthree": set(["or", "nv", "ca"]),
  "kfour": set(["nv", "ut"]),
  "kfive": set(["ca", "az"])
}
final_stations = set()

while states_needed:
  best_station = None
  states_covered = set() // 包含该广播台覆盖的所有未覆盖的州
  for station, states_for_station in stations.items():
  // covered 是一个集合，包含同时出现在 states_needed 和 
states_for_station 中的州
    covered = states_needed & states_for_station
    if len(covered) > len(states_covered):
      best_station = station
      states_covered = covered
  states_needed -= states_covered
  final_stations.add(best_station)

其他集合覆盖问题：从一堆球员中挑选符合不同要求/岗位的遴选组件团队。

贪婪算法是易于实现、运行速度快，不错的近似算法。

NP完全问题（Non-deterministic Polynomial）——多项式复杂程度的非确定性问题

NP完全问题：一类没有快速算法的问题。可通过近似算法快速找到近似解。

及时识别NP完全问题，以免浪费时间去寻找解决它们的快速算法。

旅行商问题和集合覆盖问题的一些共同之处：计算所有解从中选出最小/最短的那个，都属于NP完全问题。

聪明人都知道，不可能编写出可快速解决NP问题的算法。

易于解决的问题和NP完全问题的差别通常很小。简言之，没办法判断一个问题是不是NP完全问题，但有一些蛛丝马迹可循：

  1. 涉及“所有组合”的问题通常是NP完全问题；
  2. 如果问题可转换成集合覆盖问题或旅行商问题，则肯定是NP完全问题；
  3. 不能将问题分成小问题，必须考虑各种可能情况。可能是NP完全问题。
  4. 如果问题涉及序列（如旅行商问题中的城市序列）且难以解决，可能是NP完全问题；
  5. 如果问题涉及集合（如广播台集合）且难以解决，可能是NP完全问题；
  6. 元素较少时，算法运行速度非常快，但随元素数量的增加，速度会越来越慢；

动态规划

动态规划原理：

  • 先解决子问题，再逐步解决父问题
  • 动态规划可在给定约束条件下找到最优解
  • 在问题可分解成彼此独立且离散的子问题时

动态规划的缺陷：

  1. 没法处理背包内单个商品的一部分，必须整件考虑。
  2. 没有动态规划解决方案的公式。

设计动态规划解决方案：

  1. 每种动态规划解决方案都涉及网格；
  2. 单元格中的值通常是要优化的值；
  3. 每个单元格都是一个子问题，因此应考虑如何将问题分成子问题，这有助于找出网格的坐标轴；

动态规划的实际应用：

  1. 通过最长公共序列来确定DNA链的相似性，进而判断动物或疾病的相似性；
  2. git diff命令指出两个文件的差异
  3. 编辑距离（levenshtein distance）指出两个字符串的相似程度。编辑距离算法用途广泛，从拼写检查到判断用户上传到资料是否是盗版。
  4. Microsoft Word的断字功能，确保行长一致。

背包问题

  • 用简单算法-组合，O(2^n)
  • 贪婪算法获取近似解，可能不是最优解
  • 最优：动态规划

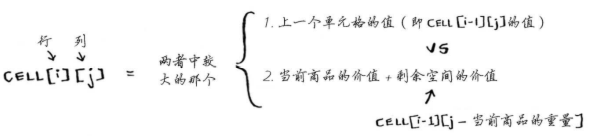
背包问题的常见约束条件：

  1. 背包空间容量
  2. 背包时间容量
- 1 2 3 4 5 6
书 3 3 3 3 3 3
相机 6 9 9 9 9 9
食物 6 9 15 18 18 18
夹克 6 9 15 18 20 23
水 6 9 15 18 20 25

如何绘制网格？

解决背包问题的网格是什么样：

  1. 单元格中的值是什么？
  2. 如何将这个问题划分为子问题？
  3. 网格的坐标轴是什么？

最长公共子串

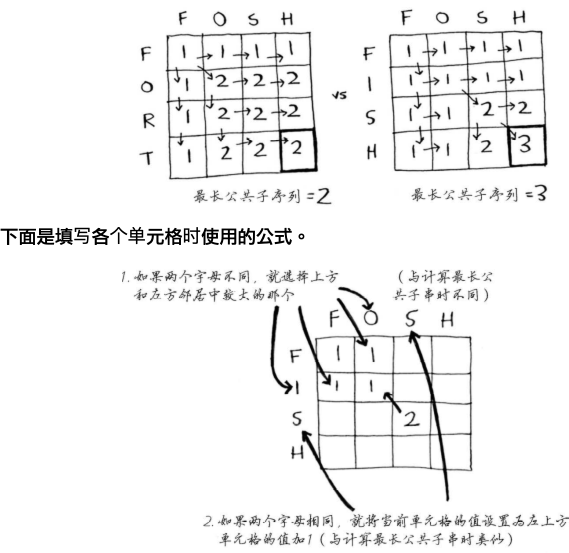
伪代码：

if word_a[i] == word_b[j]: // 两个字母相同
  cell[i][j] = cell[i-1][j-1] + 1
else:
  cell[i][j] = max(cell[i-1][j], cell[i][j-1])

费曼算法（Feynman algorithm）

步骤：

  1. 将问题写下来；
  2. 好好思考；
  3. 将答案写下来；

K最近邻算法（k-nearest neighbours, KNN）

K最近邻算法 - 分类系统

关键字：特征抽取、回归（即预测数值）

应用案例：

局限性：

特征抽取

比如：

  • 水果：个头、颜色

两个坐标点的距离=毕达哥拉斯公式=根号下((x1-x2)^2 + (y1-y2)^2)

回归（regression）

使用KNN来做两项基本工作，分类和回归：

  • 分类就是编组
  • 回归就是预测结果

实例：面包店预测当天应该烤多少面包：

  • 天气指数1-5（1很糟、5很好）
  • 是否是周末或节假日（周末或节假日为1，否则为0）
  • 有没有活动（1有，0没有）
  • 数据：
    1. A(5,1,0)=300, B(3,1,1)=225, C(1,1,0)=75, D(4,0,1)=200, E(4,0,0)=150, F(2,0,0)=50

使用KNN来预测周末+天气不错预测售出面包数f(4,1,0)：

  1. K=4, 找出K最接近的4个邻居: A,B,D,E
  2. 求均值=218.75

余弦相似度(cosine similarity), 可修整距离公式带来的“矢量距离远、实际距离近”的问题。

合适的特征

  1. 与要推荐物紧密相关
  2. 分类明确的不偏不倚的特征

和机器学习

  1. OCR（optical character recognition），Google使用OCR来实现图书数字化。

KNN提取数字特征（训练training），遇到新图时提取特征再找出最近的邻居都是谁。

比如：

  • 3: 曲线、点、曲线
  • 7: 线段、点、线段、点
  1. 垃圾邮件过滤器-使用简单算法（朴素贝叶斯分类器（Naive Bayes classifier））

研究垃圾邮件中的单词出现频率

一笔带过的内容

树

二叉查找树（BST，binary search tree），解决了二分查找速度快但插入后需重新排序的问题。

  • 每个节点的左子节点都比它小，右子节点比它大
  • O(BST)=O(logn)，最糟为O(n)；在有序数组中查找时最糟为O(logn)
  • BST的插入、删除速度快得多
普通数组 有序数组 二叉查找树
查找 O(logn) [O(1),O(logn)]
插入 O(n) O(n)
删除 O(n) O(n)

BST缺点：

  • 不能随机访问

红黑树，处于平衡状态的特殊二叉查找树；B树，特殊存储二叉树。

反向索引（inverted index）

诸如查资料时建立的索引（反向的散列表）：

  • 关键词1|资料1、资料2
  • 关键词2|资料2、资料3
  • ...

搜索引擎的基本规则。

傅立叶变换

对傅立叶变换的绝佳比喻：

  1. 给它一杯冰沙，它能告诉你其中包含哪些成分
  2. 给定一首歌曲，它能将其中的各种频率分离出来

傅立叶变换非常适合用于处理信号。

使用实例：mp3、JPG、地震预测、DNA分析

mp3和JPG（剔除不重要的音符、像素）

并行算法

速度提升是非线性的，单核变双核，算法速度也不可能提高一倍，其原因是：

  1. 并行性管理开销
  2. 负载均衡

MapReduce - 映射减肥

MapReduce 是一种流行的分布式算法。

分布式算法，执行数十亿、数万亿行进行复杂的sql查询，此时不能用MySQL，因为数据表行数超过10亿后它处理起来很吃力，此时可以通过hadoop来使用MapReduce。

MapReduce基于两个简单理念：映射(map)和归并(reduce)

概率型算法——布隆过滤器和HyperLogLog

  • 检查未发布过的内容
  • 判断未搜集过的网页
  • 判断URL是否在恶意网站清单中

海量数据如何仍使用散列表，将占用巨量的存储空间。

布隆过滤器是一种概率型数据结构，它的答案可能不对但可能正确。

HyperLogLog类似于布隆过滤器，判断搜索是否包含在日志（历史记录）中。

SHA算法（secure hash algorithm）

给定一个字符串，SHA返回其散列值。

SHA判断比较超大型文件时很有用。

SHA是一系列算法（目前，SHA-0和SHA-1已被发现缺陷）

当前最安全的密码散列函数是bcrypt

局部敏感的散列算法——Simhash

希望如果对一个字符串进行细微修改，生成的散列值只存在细微差别，以通过比较散列值来判断两个字符串的相似程度。

  • Google通过Simhash判断网页是否已搜集
  • 老师使用Simhash判断论文是否抄袭
  • Scribd允许用户上传文档或图书，但不希望上传有版权的内容

检查两项内容的相似度。

Diffie-Hellman 密钥交换

如何对消息进行加密，以便只有收件人能看懂。

  • 双方无需知道加密算法，不必会面协商要使用的加密算法
  • 破解加密的消息比登天还难
  • 公钥和私钥

其代替者：RSA

线性规划

最酷的算法之一。

用于在给定约束条件下最大限度地改善指定的目标。

所有的图算法都可以使用线性规划来实现。

线性规划是一个宽泛的多的框架，图问题只是一个子集。

线性规划使用 Simplex 算法。

posted @ 2023-07-31 09:51  汪淼焱  阅读(47)  评论(0)    收藏  举报