树状数组

树状数组

为了描述方便，以下数组下标都从1开始。

功能

给定一个数组a[n]，要求单点修改和区间查询

• 普通数组
  • 单点修改：时间复杂度：O(1)
  • 区间查询：时间复杂度：O(n)
• 前缀和数组
  • 单点修改：O(n)
  • 区间查询：O(1)

我们发现这两种办法的单次操作复杂度都是O(n)，而树状数组能达到O(logn)

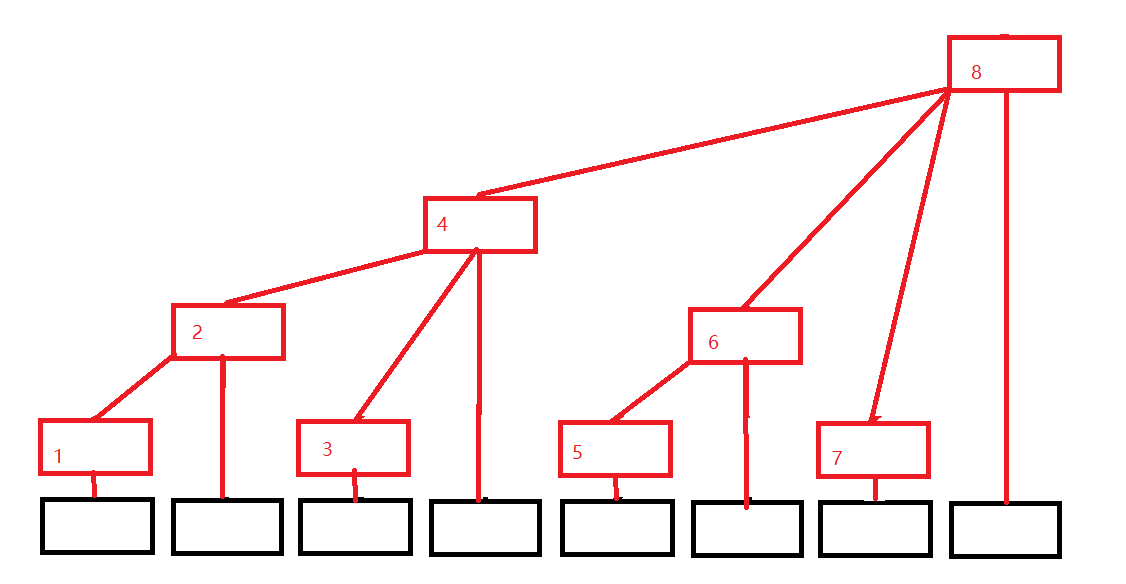
树状数组思路

树状数组形式上有点像前缀和数组，我们设为c[n]。如果是前缀和数组，那么c[i]的意义就是 a[i]+a[i-1]+……+a[1]，其管辖的区间长度为i。

而数状数组c[i]的管辖区间是2^k，那么这个k是多少呢？

max(k | i % (2^k) == 0)​。

什么意思呢？我们假设i=24,%是取余数的意思，那么24 % 1(2的0次方也算哦) == 0, 24 % 2 == 0, 24 % 4 == 0, 24 % 8 == 0, 24 % 16 != 0，那么这个k=3(8==2^3)，所以c[24]的管辖区间长度就是2^3=8，也就是a[24]+a[23]+……+a[17]。

再举一个例子i=5，因为5%1 == 0, 5%2 != 0，那么k=0，所以c[5]的管辖区间长度就是2^0=1，c[5]=a[5]。

为什么要设c[i]的管辖区间长度为2的幂次？

我们有一个结论，任何一个整数b都可以分解为有限个2幂次的和，公式表示就是\(b = 2^{k1}+2^{k2}+…+2^{kn}\)。

举个例子b=7，那么\(7 = 2^0+2^1+2^2\)。

如果这个b=7是我们要求的前缀和的长度呢？

我们设前缀和为p[7]，那么就可以找三个c[i]加起来：c[7]+c[6]+c[4]，这三个c[i]的长度就是\(2^0,2^1,2^2\)，并且c[7]=a[7], c[6]=a[6]+a[5], c[4]=a[4]+a[3]+a[2]+a[1]，也就是p[7] = c[7]+c[6]+c[4]。

为什么要得到前缀和？得到前缀和我们就能求出任何一个区间的和了。

那么这个7,6,4是哪里来的呢？6 = 7 - c[7]的管辖区间长度，4 = 6 - c[6]的管辖区间长度。那么我们现在的目标就是快速找到c[i]的管辖区间长度。我们给出一个位运算表达式：管辖区间长度=i&(-i)。

求和函数

int lowbits (int x) { //快速求管辖区间长度
    return x&(-x);
}

int getsum(int i) {
    int res = 0;
    while(i>0) {
        res += c[i];
        i -= lowbits(i);
    }
    return res;
}

如何进行单点修改呢？

我们首先要搞清楚单点修改会影响哪些c[i]的值？如果a[j]要影响c[i]，那么a[j]一定在c[i]的管辖范围内。也就是说\(i-j \le lowbits(i) \Longrightarrow i\le j+lowbits(i)\)。

单点修改函数：

void update(int i, int k) {//第i个元素加k
    while(i <= n) {
        c[i] += k;
        i = i + lowbits(i);
    }
}

类接口

/*
    单点修改，区间查询
    满足：
        结合律 ： (x op y) op z = x op (y op z)
        可差分 ： 由(x op y) 和 x 可求出 y

    初始化n为数组长度
    query[l,r] 和 update的下标都是从1开始
*/
template<class T>
class BIT{
    vector<T> c;
    int n;
    int lowbits (int x) { //快速求管辖区间长度
        return x&(-x);
    }
public:
	// 不同op，初始化值也不同
    BIT(int n) : c(n+5, 0), n(n) {}
    
    T query(int i) {
        T res = 0;
        while(i>0) {
			res += c[i]; 
			i -= lowbits(i); 
		}
        return res;
    }

    T query(int l, int r) {
        return query(r) - query(l-1);
    }

    void update(int i, T k) {//第i个元素加k
        while(i <= n) {
            c[i] += k;
            i = i + lowbits(i);
        }
    }
};

区间和，区间修改，单点查询也可以用树状数组，用树状数组维护差分数组，区间修改就转化为单点修改，单点查询就转化为区间查询，通过树状数组模板2：https://www.luogu.com.cn/problem/P3368

#include <iostream>
#include <vector>
#include <string>
#include <algorithm>
#include <numeric>
#include <map>
#include <cmath>
#include <functional>

using namespace std;
#define FUCK(x) cout << (#x) << ": " << x << endl<< endl;
#define FUCKK(x, y) cout << (#x) << ": " << x << endl << (#y) << ": " << y << endl<< endl;
#define FUCKKK(x, y, z) cout << (#x) << ": " << x << endl << (#y) << ": " << y << endl << (#z) << ": " << z << endl<< endl;
inline int log2(int n) { return log(n)/log(2); }
// inline int pow2(int n) { return 1<<n; }
inline int read()
{
	int x=0,f=1;char ch=getchar();
	while (ch<'0'||ch>'9'){if (ch=='-') f=-1;ch=getchar();}
	while (ch>='0'&&ch<='9'){x=x*10+ch-48;ch=getchar();}
	return x*f;
}

void show_bits(void *ptr, int len)
{
	unsigned char *p = (unsigned char*) ptr;
	for(int i = len-1; i >= 0; --i)
	{
		for(int j = 7; j >= 0; --j)
		{
			printf("%u", (p[i]>>j)&1);
		}
	}
	printf("\n");
}
const int MAX = INT32_MAX;
const int MIN = INT32_MIN;
using ll = long long;

int init = []()
{
	#ifdef LOCAL
		freopen("in.txt", "r", stdin);
	#endif
	ios::sync_with_stdio(false);
    cin.tie(NULL);
    cout.tie(NULL);
	return 0;
}();

/*
    单点修改，区间查询
    满足：
        结合律 ： (x op y) op z = x op (y op z)
        可差分 ： 由(x op y) 和 x 可求出 y

    初始化n为数组长度
    query[l,r] 和 update的下标都是从1开始
*/
template<class T>
class BIT{
    vector<T> c;
    int n;
    int lowbits (int x) { //快速求管辖区间长度
        return x&(-x);
    }
public:
	// 不同op，初始化值也不同
    BIT(int n) : c(n+5, 0), n(n) {}
    
    T query(int i) {
        T res = 0;
        while(i>0) {
			res += c[i]; 
			i -= lowbits(i); 
		}
        return res;
    }

    T query(int l, int r) {
        return query(r) - query(l-1);
    }

    void update(int i, T k) {//第i个元素加k
        while(i <= n) {
            c[i] += k;
            i = i + lowbits(i);
        }
    }
};


int main()
{
	int n, m; cin >> n >> m;
	BIT<int> bitree(n);
	vector<int> arr(n);
	int i = 1;
	// 初始化差分数组
	for(auto &a : arr) {
		cin >> a;
		bitree.update(i, i==1?a:a-arr[i-2]);
		++i;
	}

	while(m--)
	{
		int op; cin >> op;
		if(op == 1)
		{
			int l, r, k;
			cin >> l >> r >> k;
			// 数组区间[l,r]加上k 等价于 差分数组d[l]+k, d[r+1]-k
			bitree.update(l, k);
			bitree.update(r+1, -k);
		} else {
			int indx;
			cin >> indx;
			// 求数组[indx]等价于求差分数组 sum(d[1,indx])
			cout << bitree.query(indx) << endl;
		}
	}
    return 0;
}