数理统计

概率论参考文章

5.1 总体与样本

总体与个体

把研究一群研究对象称作总体，每个研究对象称为个体。

例如：我们研究一群学生的身高。看似总体是一群学生，个体是每个学生。实际上总体是一群数字，个体是每一个数字。在这个总体中，有的数字出现的多，有的出现的少，因此用一个概率分布去描述这个总体是很合适的，从这个角度，总体就是概率分布。

样本

为了了解总体的分布，我们从总体中随即抽取n个个体，称之为总体的一个样本。n为样本容量，样本中的个体称之为样品

• 样本具有随机性：即总体中每个个体被抽到的概率相等
• 样本要有独立性：即每个样本的的取值，不影响其他样本的抽取

分组样本

抽取样本的观测值没有具体的数值，只有一个范围

例如：总体是一群学生的身高，(160-170)有10人，(170-180)有20人,(180-~)有10人。

5.2 样本数据的整理与显示

经验分布函数

设\(x_i\)是样本个体，假设\(x_i\)是有序样本，定义如下函数：

\(F_n(x)=\begin{cases}0,& x<x_1 \\ k/n,&\ x_k\le x<x_{k+1},k=1,2,\cdots,n-1 \\ 1,& x\ge x_n \end{cases}\)

频数频率分布表

对样本数据

1. 对样本进行分组：确定组数k，平均每组样品3，4个

2. 确定每组组距：$$d = \dfrac{(max-min)}{组数}$$

3. 确定每组组限：$$a_0,a_0+d=a_1,a_0+2d=a_2,\cdots$$ 形成一下区间$$(a_0,a_1],(a_1,a_2],\cdots,(a_{k-1},a_k]$$ 。

4. 统计样本数据落入每个区间的个数（频数），并列出其频数频率分布表

   -----分组区间----	-----组中值----	频数	频率
   \((a_0,a_1]\)	\(\dfrac{a_0+a_1}{2}\)
   ...	...
   \((a_{k-1},a_k]\)	\(\dfrac{a_{k-1}+a_k}{2}\)

直方图和茎叶图

略。

5.3 统计量及其分布

样本来自总体，因此样本中含有总体各个方面的信息，但这些信息较为分散，为将这些分散的信息集中起来反应总体的各种特征，需要对样本加工，最常用的方法是构造样本的函数，不同的函数反应总体的不同特征。

均值及其抽样分布

样本均值用\(\bar x\)表示：

\[\bar x = \dfrac{x_1+\cdots+x_n}n=\dfrac1 n\sum\limits_{i=1}^nx_i \]

在分组样本的场合：

\[\bar x = \dfrac{x_1f_1+\cdots+x_kf_k}{n}\;\;\;(n=\sum\limits^k_{i=1}f_i) \]

其中\(k\)为组数，\(x_i\)为第\(i\)组的组中值，\(f_i\)为第\(i\)组的频数

方差与标准差

• 方差\(s^2_* = \dfrac1 n \sum\limits^n_{i=1}(x_i-\bar x)^2\)

• 标准差：\(s^2_*=\sqrt{s^2_*}\)

• 无偏方差：\(s^2 = \dfrac1 {n-1} \sum\limits^n_{i=1}(x_i-\bar x)^2\)

在这个定义中：\(\sum\limits^n_{i=1}(x_i-\bar x)^2\) 称之为偏差平方和，\(n-1\)称之为偏差平方和的自由度。

• 总体分布为\(N(\mu,\sigma^2)\)，则\(\bar x\)的精确分布为\(N(\mu,\sigma^2/n)\)。
• 若总体不是正态分布，\(\bar x\) 渐进分布为\(N(\mu,\sigma^2/n)\)。

样本矩及其函数

• \(k\)阶原点矩：$$a_k=\dfrac1 n \sum x_i^k$$ ,一阶原点矩就是均值
• \(k\)阶中心距：$$b_k=\dfrac1 n \sum(x_i-\bar x)^k$$,二阶中心距就是方差。

当总体关于分布中心对称时，用\(\bar x,s\)刻画总体的特征就很有代表性。

当不中心对称时，我们需要引入样本偏度和样本峰度来刻画总体。

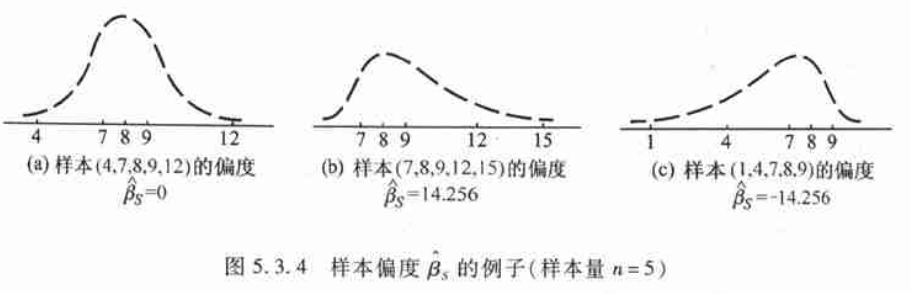
样本偏度(中心距的函数)

反映总体分布与对称性的偏离方向及程度

\[\hat \beta_s=b_3/b_2^{3/2} \]

样本峰度

\(\hat \beta_k=\dfrac{b_4}{b_2^{2}}-3\)

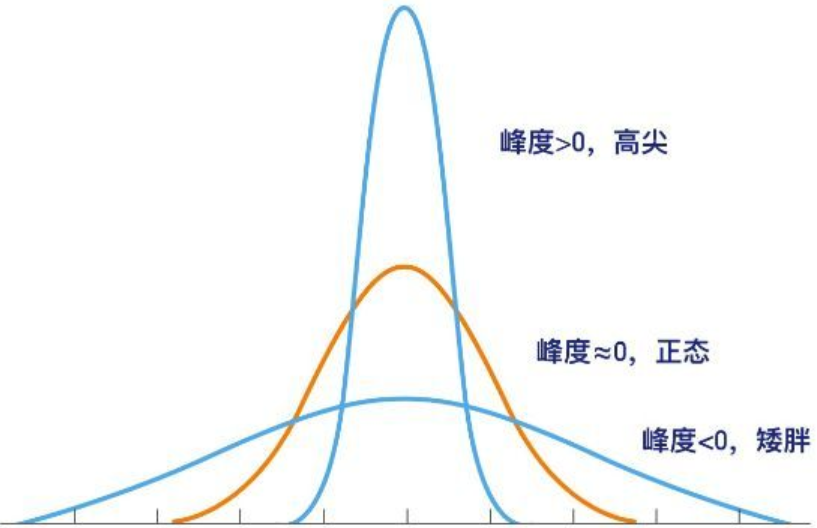
反映总体分布曲线在其峰值附近的陡峭程度和尾部粗细的统计量。

当\(\hat\beta_k\)明显大于0，陡峭，尾部细。

次序统计量及其分布

对样本\(x_1,x_2,\cdots,x_n\)从小到大排序,第\(i\)个就是样本的第\(i\)次序统计量，记作\(x_{(i)}\)。

单个次序统计量的分布

设总体\(X\)的密度函数\(p(x)\),分布函数\(F(x)\),则第\(k\)次序统计量的密度函数为

\[p_k(x)=\dfrac{n!}{(k-1)!(n-k)!}(F(x))^{k-1}(1-F(x))^{n-k}p(x) \]

多个次序统计量的联合分布

\[p_{ij}(y,z) = \dfrac{n!}{(i-1)!(j-i-1)!(n-j)!} [F(y)]^{i-1}[F(z)-F(y)]^{j-i-1}[1-F(z)]^{n-j}p(y)p(z),y\le z \]

5.4 三大抽样分布

\(\chi^2\) 分布（卡方分布）

充分性

\(p(x_1,x_2,...,x_n;\theta) = g(T(x_1,x_2,...,x_n);\theta)h(x_1,x_2,...,x_n)\) .

估计量

给出估计

距估计

样本矩代替总体距，用\(\dfrac 1 n\sum\limits_{i=1}^nX_i^s\)代替\(E(X_s)\).

有几个未知参数，就列几个方程\(\begin{cases} E(X) = \mu \\ E(X^2) = E^2(X)+Var(X)\end{cases}\) .

极大似然估计

总体分布列为\(P(X=x)=p(x;\theta),\theta\)为未知参数. \(x_1,x_2,...,x_n\)为样本观测值，

\(L(\theta) = P(X_1=x_1,...,X_n=x_n)=p(x_1;\theta)...p(x_n;\theta)\). 为似然函数，选取\(\theta\),使\(L(\theta)\)的值尽量大。

离散情况下，\(p(x;\theta)\)是分布列，连续情况下是密度函数。

1. 先写出似然函数
2. 对似然函数取对数，求导，求最大值。

评价估计

无偏性

\(E(\hat \theta) = \theta\).

有效性(无偏估计才能进行比较)

\(Var(\hat \theta_1) \le Var(\hat\theta _2)\\E[(\hat\theta-E(\hat \theta))^2]\)

相合性

\(lim_{n\rightarrow +\infty}P(|\hat\theta_n-\theta|<\epsilon)=1\).

区间估计

对给定的\(\alpha\),\(P_{\theta}(\hat\theta_L\le\theta\le\hat\theta_U)\ge1-\alpha\) ，称随机区间\([\hat\theta_L,\hat\theta_U]\)为\(\theta\)的置信水平为\(1-\alpha\)的置信区间。

事先给定\(1-\alpha\)，再求置信区间。

枢轴量法

1. 构造\(G=G(x_1,x_2,...,x_n,\theta)\),分布已知，不依赖于任何未知参数
2. 选择两个常数，使得\(P(c\le G\le d)=1-\alpha\).。。。。
3. 将\(c\le G\le d\)变形为\(\hat\theta_L\le \theta\le\hat\theta_U\)置信区间

（正态）已知\(\sigma\)求\(\mu\)的置信区间

选取枢轴量\(G=\frac{\bar x-\mu}{\sigma/\sqrt n}\sim N(0,1)\), 置信区间为\(\bar x\pm U_{1-\frac\alpha 2}\dfrac {\sigma}{ \sqrt n}\)

（正态）未知\(\sigma\)求\(\mu\)的置信区间

选取枢轴量\(G=\frac{\bar x-\mu}{s/\sqrt n}\sim t(n-1)\), 置信区间为\(\bar x\pm t_{1-\frac\alpha 2}(n-1)\dfrac {s}{ \sqrt n}\)

（正态）\(\mu\)未知求\(\sigma ^2\)的置信区间

选取枢轴量\(\chi^2=\frac{(n-1)s^2} {\sigma^2}\sim \chi^2(n-1)\), 置信区间为\([\frac{(n-1)s^2}{\chi^2_{1-\alpha/2}(n-1)},~\frac{(n-1)s^2}{\chi^2_{\alpha/2}(n-1)}]\) .

两个正态总体下的置信区间

\(\mu_1-\mu_2\)的置信区间

1. \(\sigma_1^2和\sigma_2^2\)已知时的两样本\(u\)区间

   选取枢轴量\(u=\dfrac{\bar x-\bar y-(\mu_1-\mu_2)}{\sqrt{\dfrac{\sigma^2_1}{m}+\dfrac{\sigma^2_2}{n}}}\) ,置信区间为\(\bar x-\bar y\pm u_{1-\alpha/2}\sqrt{\dfrac{\sigma_1^2}{m}+\dfrac{\sigma^2_2}{n}}\)

2. \(\sigma_1^2=\sigma_2^2=\sigma^2\)未知时的两样本\(u\)区间

假设检验

势函数（拒绝的概率）

尽量不要拒绝原假设，也就是\(g(\theta)\)尽量小。

\(g(\theta)=P_\theta(X\in W),W\)为拒绝域 ，\(g(\theta)\)为拒绝的概率，犯错误的概率\(\begin{cases}\alpha(\theta)=g(\theta)&\theta\in\Theta_0\\\beta(\theta)=1-g(\theta)&\theta\in\Theta_1 \end{cases}\)

\(\alpha=P(x\in W)\)

正态\(\sigma\)已知\(u\)检验