线性规划（应付考试）

普通单纯型法

\(maxZ = x_1+2x+x_3\\\begin{cases} 2x_1-3x_2+2_3\le15 \\ \frac1 3 x_1 + x_2+5x+3\le20 \\ x_1,x_2,x_3\ge0\end{cases}\)

step 1:化为标准型

设松弛变量\(x_4,x_5\)

\(maxZ = x_1+2x+x_3\\\begin{cases} 2x_1-3x_2+2_3+x_4=15 \\ \frac1 3 x_1 + x_2+5x+3+x_5=20 \\ x_1,x_2,x_3,x_4,x_5\ge0\end{cases}\)

step 2:画表

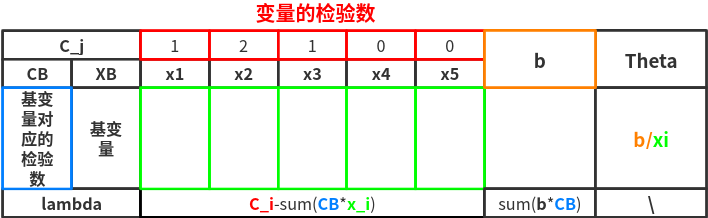
1. 判断是否已经是最优解
   1. \(lambda\le0\)：就是最优解
   2. \(lambda>0\)：
      1. 对应的\(x_i\)全部小于等于0：无界解
      2. 对应的\(x_i\)有大于0的：进行第2步
   3. 存在非基变量检验数为0，多重最优解。
2. 如果不是最优，选lambda最大的为入基变量，Theta最小的为出基变量(xi若小于0则Theta值不存在) .
3. 将lambda和Theta交叉的元素通过行初等变换，使这个元素所在列的元素都为0。
4. 回到第1步。

大M

\(maxZ = 3x_1+2x_2-x_3 \\ \begin{cases}-4x_1+3x_2+x_3 \ge 4 \\ x_1-x_2+2x_3\le10 \\ 2x_1-2x_2+x_3=1 \\ x_j\ge0,j=1,2,\cdots,5 \end{cases}\)

step 1. 化为标准型

系数矩阵没有单位矩阵，添加人工变量\(x_6,x_7\) ，目标函数加入\(-Mx_6-Mx_7\) ，\(M\)代表无穷大

\(maxZ = 3x_1+2x_2-x_3-Mx_6-Mx_7 \\ \begin{cases}-4x_1+3x_2+x_3-x_4+x_6=4 \\ x_1-x_2+2x_3+x_5=10 \\ 2x_1-2x_2+x_3+x_7=1 \\ x_j\ge0,j=1,2,\cdots,7 \end{cases}\)

step 2. 用普通单纯型法解

若最优解中有\(M\),则原问题无解。

两阶段单纯型法

step 1. 用大M法的 step 1.

step 2. 构造第一阶段问题

\(minw=x_6+x_7\\\begin{cases}-4x_1+3x_2+x_3-x_4+x_6=4 \\ x_1-x_2+2x_3+x_5=10 \\ 2x_1-2x_2+x_3+x_7=1 \\ x_j\ge0,j=1,2,\cdots,7 \end{cases}\)

1. \(w\)最优解为0，利用第一阶段的最后一步继续进行大M法解原问题。
2. \(w\)最优解不为0，原问题无解。