网络流学习笔记

短时间内可能会不时更新这个系列，学了网络流的新东西或新题就扔在这吧，望周知。

最大流

模板：P3376 【模板】网络最大流

性质

设 \(f(u,v)\) 表示 \(u \rightarrow v\) 的流量， \(c(u,v)\) 表示 \(u \rightarrow v\) 的限制。

1. \(f(u,v) \le c(u,v)\) （显然）

2. \(f(u,v) = -f(v,u)\) 可以理解为 \(u\) 向 \(v\) 流 \(x\) 的流量，相当于 \(v\) 向 \(u\) 流 \(-x\) 的流量。

3. \(\sum_{u,v} f(u,v) = 0\)（希望读者自证）

几个定义

ps：这几个定义对于网络流的题目都适用，包括但不限于最大流

残量网络：每条边剩下的流量所构成的网络。

设 \(r(u,v)\) 表示残量网络，初始时 \(r(u,v) = c(u,v)\)。操作后 \(r(u,v) = c(u,v) - f(u,v)\)。由于 \(\sum_{v} f(u,v) = 0\)，所以 \(\sum_{v} r(u,v) = \sum_{v} c(u,v)\) 是恒成立的。

残量网络中一条没有边容量为 \(0\) 的路径叫做增广路。

因为流完这条路径会使流量增加，所以叫做增广路。

为了保持平衡，每增广一次不仅让正向边的流量变小，还使反向边的流量增大相同的数量。

可以理解为从反向边流正向增广的数量相当于撤销了一次增广操作。

定理：不停寻找增广路直到无法增广就可以找到最大流。

证明：由最大流的定义可得最大流的流量是全图流量的总和，如果有增广路则一定不是最大流，证毕。

做法

Ford-Fulkerson(FF)

最简单且复杂度最劣的算法，\(O(m \times 最大流量)\) 的算法。

即不停 dfs 寻找增广路，直到无法增广。

但是

关于 FF，他死了。

举个栗子：

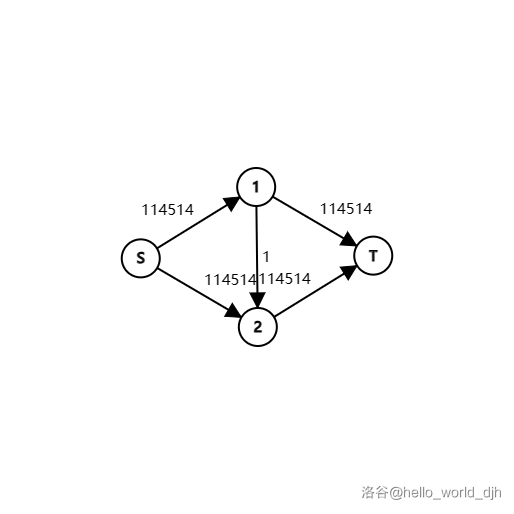
显然，这个图的最大流为 \(229028\)。

但是程序的运行方式超出我们预期。

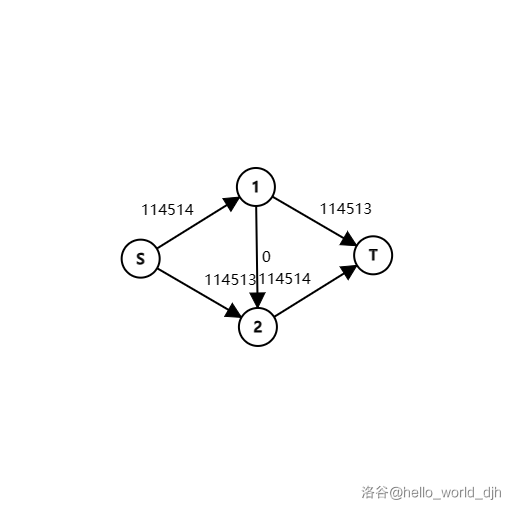
他会增广 \(S \rightarrow 1 \rightarrow 2 \rightarrow T\) 这条边，并将这条流上所有的反向边增加 \(1\)。

然会他会增广 \(S \rightarrow 1 \rightarrow 2 \rightarrow T\) （ \(f(1,2)\) 相当于 \(f(1,2)\) 的反向边）。

然后他就会一直重复这两个操作直到 \(f(S,1),f(1,T),f(S,2),f(2,T)\) 都为 \(0\) 时找到最大流 \(229028\)。

所以要引出本文的重点：

dinic(和ISAP)

先介绍 dinic，因为 ISAP 类似于 dinic 的一个较强的优化。

dinic 的核心很好理解，就是通过把所有点分在不同的层数。

举个栗子：

\(T\) 在第一层，\(1,2\) 在第二层，\(S\) 在第三层。

所以我们只需要在增广的时候判断下一个点的层数是不是当前点的层数加一即可。

也就是只有 dep[v] + 1 = dep[u] 时才增广 \(f(u,v)\)。

因为我本人没有写过无优化版 dinic，所以这里不放代码。

优化：当前弧优化

也就是之前增广过的边一定不用再管了。

这个优化让 dinic 质变，单次增广复杂度从最差 \(O(nm^2)\) 变成稳定的 \(O(nm)\) 的。

注：哪怕用了 ISAP 也务必带着这个优化。

由于我也没写过优化后的 dinic，所以这里不放代码。

其实按理说 ISAP 比 dinic 快很多，但是因为 dinic 写的人太多，所以再毒瘤的出题人也会留着这个做法。

接下来的都是 ISAP 的讲解了。

ISAP 和 dinic 的不同是 ISAP 引入了一个叫 gap 的概念，代表某一层中剩余的点的数量。如果有一个层的 gap 为零就停止本次增广。

bfs 再改成从 T 开始迭代，你会发现这样可以使我们只 bfs 一遍，dfs \(n\) 遍即可。

稍微优化了一下整体复杂度，从 dinic 的 \(O(n^2m)\) 优化到了 \(O(nm + m)\) （与 \(O(nm)\) 同阶）。

听起来很夸张的优化，但是如果你真的做题你会发现差别不大，有的时候最优解都抢不过卡常的优化 dinic。

同样的，当前弧优化也适用于ISAP。

这里贴一下代码：

ISAP代码

//code by hello_world_djh
#include <bits/stdc++.h>

//省略快读

typedef long long ll;
const int N = 210, M = 5010;
const ll INF = (1ll << 31) - 1;

struct Edge {
    int to, nxt;
    ll w;
} edge[M << 1];
int n, m, s, t, tot = 1, head[N], cur[N], dep[N], gap[N];
ll maxflow;

void add(int u, int v, ll w) {
    edge[++tot] = Edge{v, head[u], w};
    head[u] = tot;
    return;
}

void bfs() {
    memset(dep, -1, sizeof dep);
    memset(gap, 0, sizeof gap);
    std::queue <int> q;
    dep[t] = 0;
    gap[0]++;
    q.push(t);
    while (!q.empty()) {
        int u = q.front();
        q.pop();
        for (int i = head[u]; i; i = edge[i].nxt) {
            int v = edge[i].to;
            if (~dep[v]) continue;
            dep[v] = dep[u] + 1;
            gap[dep[v]]++;
            q.push(v);
        }
    }
    return;
}

ll dfs(int u, ll flow) {
    if (u == t) {
        maxflow += flow;
        return flow;
    }
    ll used = 0;
    for (int &i = cur[u]; i; i = edge[i].nxt) {
        int v = edge[i].to;
        if (edge[i].w && dep[v] + 1 == dep[u]) {
            ll d = dfs(v, std::min(edge[i].w, flow - used));
            if (d) {
                edge[i].w -= d;
                edge[i ^ 1].w += d;
                used += d;
            }
            if (used == flow)
                return used;
        }
    }
    --gap[dep[u]];
    if (!gap[dep[u]])
        dep[s] = n + 1;
    dep[u]++;
    gap[dep[u]]++;
    return used;
}

ll ISAP() {
    bfs();
    while (dep[s] < n) {
        memcpy(cur, head, sizeof head);
        dfs(s, INF);
    }
    return maxflow;
}

int main() {
    n = read<int>();
    m = read<int>();
    s = read<int>();
    t = read<int>();
    for (int i = 1, u, v; i <= m; i++) {
        u = read<int>();
        v = read<int>();
        ll w = read<ll>();
        add(u, v, w);
        add(v, u, 0);
    }
    printf("%lld\n", ISAP());
    return 0;
}