平衡树专题
前言
继续水长度
上期线段树我们说过lhy26老师六个月才写了一篇博客不到一半,现在我要帮他写一下这篇他至今没写完但错误甚多的博客
本文所有操作默认为luoguP3369 【模板】普通平衡树
STL
实际上,我们知道,万能的STL能实现几乎所有数据结构,只是常数大了不止一点半点
vector
包含在头文件#include<vector>,相当于一个支持o(1)插入和查询的无限长数组。
其定义方式是vector<T> v,T是任意类型(struct必须有重载函数)
我们主要使用insert和erase操作,支持在某个指针处插入或删除一个值
两个封装好的指针begin和end,分别指向vector首个位置和最后一个位置的下一个位置
lower_bound和upper_bound
两个二分查询的函数,包含在#include<algorithm>里
都是传三个参数,一个是头指针,一个是尾指针的下一个,最后一个是寻找的值
由于二分查找的局限性,查找的数组必须是升序排列好的
进入正题
接下来我们考虑怎样用这些操作实现复杂的普通平衡树
根据我们小学二年级学过的插入排序,我们可知插排就是在一个已经排过序的数组中插入到该插入的位置
这个给了我们将vector和lower_bound结合的思路
剩下的操作同理
我们因为有一个排好序的数组,所以我们可以用lower_bound和upper_bound实现前驱后继,查询排名,查询该排名的数
插入
同上:
点击查看代码
inline void ins(int val)
{
v.insert(std::lower_bound(v.begin(),v.end(),val),val);
return;
}
删除
只需找到该数的位置,直接删除
点击查看代码
inline void del(int val)
{
v.erase(std::lower_bound(v.begin(),v.end(),val));
return;
}
查询排名
lower_bound基本操作
点击查看代码
inline int getrank(int val)
{
return std::lower_bound(v.begin(),v.end(),val)-v.begin()+1;
}
查询数值
vector基本操作
点击查看代码
inline int getnum(int rank)
{
return v[rank-1];
}
前驱
可以理解为第一个出现的位置的上一个位置,题目保证有解
点击查看代码
inline int pre(int val)
{
return *--std::lower_bound(v.begin(),v.end(),val);
}
后继
upper_bound基本操作
点击查看代码
inline int nxt(int val)
{
return *std::upper_bound(v.begin(),v.end(),val);
}
上代码
粘一下就行了
点击查看代码
#include<cstdio>
#include<algorithm>
#include<vector>
std::vector<int> v;
inline void ins(int val)
{
v.insert(std::lower_bound(v.begin(),v.end(),val),val);
return;
}
inline void del(int val)
{
v.erase(std::lower_bound(v.begin(),v.end(),val));
return;
}
inline int getrank(int val)
{
return std::lower_bound(v.begin(),v.end(),val)-v.begin()+1;
}
inline int getnum(int rank)
{
return v[rank-1];
}
inline int pre(int val)
{
return *--std::lower_bound(v.begin(),v.end(),val);
}
inline int nxt(int val)
{
return *std::upper_bound(v.begin(),v.end(),val);
}
int n;
int main()
{
scanf("%d",&n);
while(n--)
{
int op,x;
scanf("%d%d",&op,&x);
switch(op)
{
case 1:ins(x);break;
case 2:del(x);break;
case 3:printf("%d\n",getrank(x));break;
case 4:printf("%d\n",getnum(x));break;
case 5:printf("%d\n",pre(x));break;
default:printf("%d\n",nxt(x));break;
}
}
return 0;
}
pbds
就是平板电视
支持红黑树,splay等平衡树。
没啥好讲的,还是直接上代码吧。
点击查看代码
#include <bits/stdc++.h>
#include <ext/pb_ds/assoc_container.hpp>
#include <ext/pb_ds/tree_policy.hpp>
__gnu_pbds::tree <long long, __gnu_pbds::null_type, std::less <long long>, __gnu_pbds::rb_tree_tag, __gnu_pbds::tree_order_statistics_node_update> Tree;
int main() {
int n; std::cin >> n;
for (int i = 1; i <= n; i++) {
long long k, x; std::cin >> k >> x;
switch (k) {
case 1: Tree.insert((x << 20) + i); break;
case 2: Tree.erase(Tree.lower_bound(x << 20)); break;
case 3: std::cout << Tree.order_of_key(x << 20) + 1 << std::endl; break;
case 4: std::cout << ((*Tree.find_by_order(x - 1)) >> 20) << std::endl; break;
case 5: std::cout << ((*--Tree.lower_bound(x << 20)) >> 20) << std::endl; break;
default: std::cout << (*Tree.upper_bound((x << 20) + n) >> 20) << std::endl; break;
}
}
return 0;
}
fhq_treap
定义
fhq treap(又名无旋treap),就是通过分裂(split)和合并(merge)来维护平衡树平衡的性质,相比起所有带旋转的平衡树的码量来说都少得多,就是时间复杂度和实用性稍差,但是现在fhq treap的地位正在逐渐上升,是OI界平衡树双子星之一
具体操作
构建内存池
建一个数组维护左孩子和右孩子的节点编号,该节点维护的权值,以该节点为根节点的子树大小和维护平衡插入的一个随机数
点击查看代码
struct FHQ_Treap{
int l,r;//左孩子和右孩子的节点编号
int val,size,key;//该节点维护的权值 ,以该节点为根节点的子树大小,一个随机的插入权值
FHQ_Treap()//构造函数(不加也行)
{
return;
}
};
FHQ_Treap tree[int(1e5+5)];//开数组,此题为1e5
生成随机权值
随便取几个大常数相乘,或使用c++和c标准库中的随机函数
点击查看代码
inline int rnd()//随机数生成器
{
static int x=131;
x%=999999998;
return x*=20220207;//玄学大常数相乘
}
新建节点
新建一个权值为val的节点,赋给它一个随机数权值,将size赋成初始值1,并返回该节点的编号
点击查看代码
inline int newnode(int val)//生成一个权值为val的新节点,返回节点的编号
{
tree[++cnt].val=val;//赋权值
tree[cnt].size=1;//初始size为1
tree[cnt].key=rnd();//随机一个插入的权值
return cnt;
}
更新变更的size
将该节点的size更新为左子树的size加上右子树的size再加1
点击查看代码
inline void update(int nw)//更新size
{
tree[nw].size=tree[tree[nw].l].size+tree[tree[nw].r].size+1;//左子树的size加上右子树的size在加上自己本身的1
return;
}
重头戏分裂和合并来了!
敲黑板
分裂(split)
分裂有两种,一种现在讲,另一种在文艺平衡树时讲
按值分裂
将以nw为根节点的子树以val分成以x为根节点的子树和以y为根节点的子树,nw树中小于等于val的数放在x树上,大于val的数放在y树上,根据二叉搜索树的性质可得如果根节点属于x树则左子树一定在x树上,而右子树可能在x树上,也可能在y树上,而如果根节点在y树上,则右子树一定都在y树上,左子树有可能在x树上也有可能y树上,所以按情况分别递归即可,递归终止与当当前节点为空就将左右子树的根编号赋成0即可
点击查看代码
inline void split(int nw,int val,int &x,int &y)//将根节点为nw的子树按val分裂为x树和y树
{
if(!nw)//递归终止条件
x=y=0;//赋值
else
{
if(tree[nw].val<=val)//如果当前节点要分在x树上
{
x=nw;//现将根节点加入x树
split(tree[x].r,val,tree[x].r,y);//递归,如上文
}
else
{
y=nw;//将根节点加入y树
split(tree[y].l,val,x,tree[y].l);//递归,如上文
}
update(nw);//更新当前节点的大小
}
return;
}
来一张图理解一下:
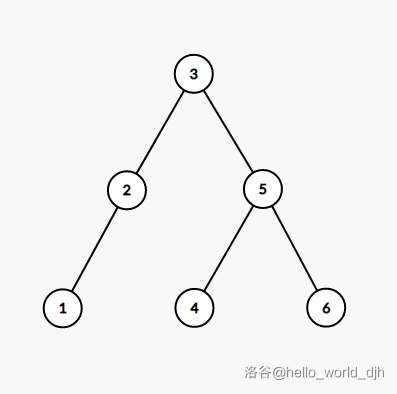
我们现在以4分裂
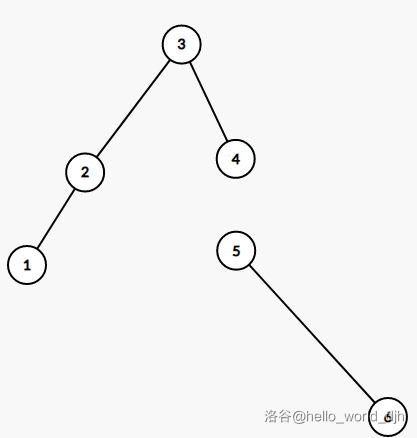
按大小分裂
主要是fhq_treap版的文艺平衡树使用
其本质思想就是将一棵树分裂成两棵树,一棵树的大小是传入的size,另一棵树的大小为该树的剩下的大小
我的程序编了一个下传标记的函数,叫push_down函数,其作用是将以传入节点的标记下传到他的左右子树上可根据情况改变该函数
上代码:
点击查看好康的
void split(int nw,int size,int &x,int &y)
{
if(!nw)
{
x=y=0;
return;
}
else
{
if(tree[nw].tg)
push_down(nw);
if(tree[tree[nw].l].size<size)
{
x=nw;
split(tree[nw].r,size-tree[tree[nw].l].size-1,tree[nw].r,y);
}
else
{
y=nw;
split(tree[nw].l,size,x,tree[nw].l);
}
update(nw);
return;
}
}
来两张图理解一下
分裂前:

现在我们按四分裂
分裂后:
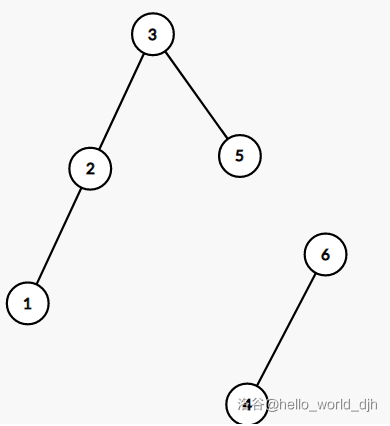
大家可以看到按四按值分裂和按四按大小分裂的效果是不一样的,因为这里的四一个是值域,一个是大小,一定要区分这两种分裂方式的区别
合并
合并就是分裂的逆过程,合并就是把两课根节点,合并成一个大树,并返回其根节点
我们按照这两个子树根节点的随机权值key作为合并标准,谁的key大谁就当根节点
实际上这里不写大于也行,毕竟我们只要求随机合并,你甚至在条件里都可以写rnd()%2,所以不必死记硬背
主要是要记住自己的合并法则即可
上代码:
点击查看代码
int merge(int x,int y)
{
if(!x||!y)
return x+y;
if(tree[x].key>tree[y].key)
{
tree[x].r=merge(tree[x].r,y);
update(x);
return x;
}
else
{
tree[y].l=merge(x,tree[y].l);
update(y);
return y;
}
}


 浙公网安备 33010602011771号
浙公网安备 33010602011771号