Machine Learning--006

Machine Learning --006

偏差、方差以及模型复杂度

问题导出：回归方法有很多。可以线性回归，可以多项式回归，可以KNN...但怎样选择、设置模型，才能更好地预测从相同分布中抽样得到的未来数据?我们必须有个有效的判断方法。

模型选择及评估

• 模型选择: 比较不同模型的表现选择最好的一个 (测试误差最小)
• 模型评估: 已经选定一个模型，在新数据上估计预测误差

偏差，方差 & 复杂度

增加模型复杂性时，总是可以减少训练误差，但是存在过度拟合（即偏差小，方差过大）的风险。
对于偏差和方差，我们有Bias-Variance Decomposition。
将模型设定为：\(Y=f(X)+\epsilon,E(\epsilon)=0,Var(\epsilon)=\sigma^2\)，我们有分解如下：

\[Err(x_0)=E[(Y-\hat f(x_0))^2|X=x_0] =\sigma_\epsilon^2+[E\hat f(x_0)-f(x_0)]^2+E[\hat f(x_0)-E\hat f(x_0)]^2\]

第一项为噪声，必然存在的误差。第二项为\(\hat f(x_0)\)的Bias。第三项为\(\hat f(x_0)\)的Var。

线性模型的偏差还可以继续分解：

\[Bias^2 = E[f(x_0)-\beta^T_*x_0]^2+E[\beta^T_*x_0-E\hat \beta_\alpha x_0]^2 \]

第一项为平均模型偏差。第二项为平均估计误差。
下图能比较直观地展示Bias、Variance之间的关系。

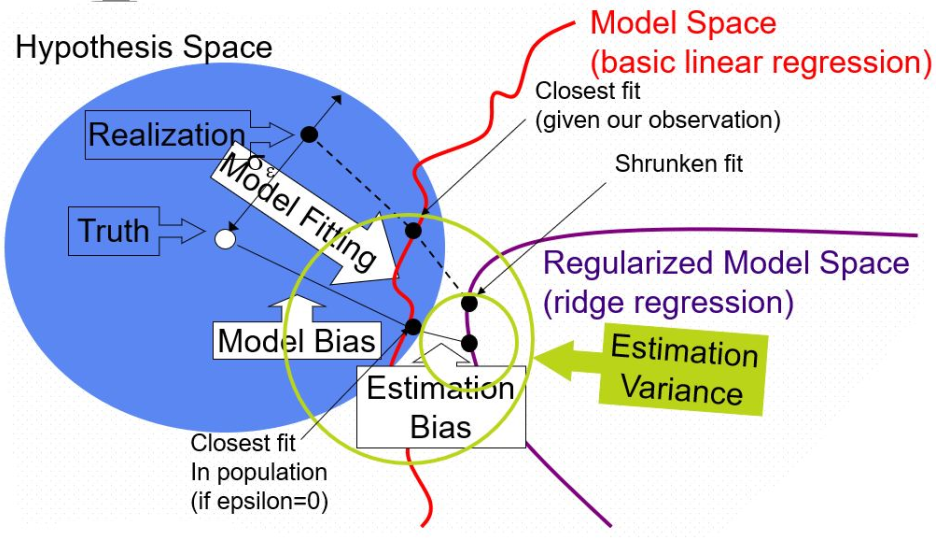
对于Bias-Variance Decomposition，我们有两个例子：

• knn回归：

\[Err(x_0) = \sigma^2_\epsilon+[f(x_0)-\frac{1}{k}\sum^k_{l=1}f(x_{l})]^2+\frac{\sigma^2_{\epsilon}}{k} \]

• 线性回归:

\[Err(x_0) = \sigma^2_\epsilon+[f(x_0)-E\hat f_p(x_0)]^2+||h(x_0)||^2\sigma^2_{\epsilon} \]

上面两种方法随k（p）变化如下：

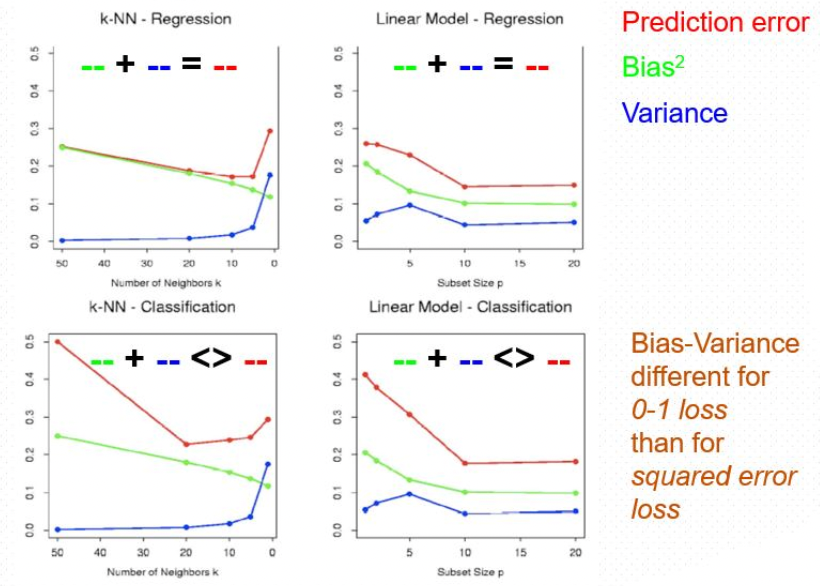
可以看到，KNN方法中，Var随k增大而减小，且形状像反比例函数，这与其err分解式的形式有很大关系。而线性回归的变化也易从err表达式看出来，是近线性的。

优化模型

训练误差优化

通常，train loss < test loss。虽然不是绝对但当程序中很多epoches皆满足如此关系的话，那就最好检查下程序本身是否有问题。
训练误差计为：

\[\bar {err} = \frac{1}{N}\sum^N_{i=1}L(y_i,\hat f(x_i)) \]

测试误差记为：

\[err = EL(Y,\hat f(X)) \]

为了估计这两个err之间的差距，我们通过下面的计算得到。
样本内误差可以由下式计算得到：

\[Err_{in} = \frac{1}{N}\sum ^N_{i=1}E_yE_Y^{new}L(Y_i^{new},\hat f(x_i)) \]

进一步可以得到：

\[Err_{in}=E_y(\bar {err})+\frac{2}{N}\sum^N_{i=1}Cov(\hat y_i,y_i) \]

对于有 d 个自变量的线性拟合，偏差函数为

\[Err_{in} = E_y(\bar {err})+\frac{2}{N}d\sigma^2_\epsilon \]

故因此，\(Err_{in}\)随d增大而增大，随样本增大而减小。

样本内误差估计

样本内误差估计（并非MAE/MSE那种直接计算出来的，而是对其量级进行一个大概的估计）：

• AIC
  \(AIC=2k−ln( L)\)，这里k是模型中的待估参数数量，\(\hat L\)是该模型极大似然估计的最大值。AIC 值越小，说明该统计模型损失的信息越少，模型越好。这其实很好理解。2k限制了参数数量，\(ln(L)\)则选出了一定参数数量下下误差最小的参数。
• BIC
  \(BIC = k\ln(n)-2\ln(L)\)，AIC存在的不足之处：当样本容量很大时，在 AIC 准则中拟合误差提供的信息就要受到样本容量的放大，而参数个数的惩罚因子却和样本容量没关系。因此当样本容量很大时，使用 AIC 准则选择的模型不收敛于真实模型，它通常比真实模型所含的末知参数个数要多。BIC准则也引入了与参数相关的惩罚项，相对 AIC 而言，BIC 考虑 了样本量，效果更好。
• MDL
  最小描述长度原则。长度计算方法图下：\(length = −lnPr(y|θ; M; X) − lnPr(θ|M)\)。前面部分是在给定模型下给出模型 + 最优编码的差异传输长；后面部分是最优编码下模型的描述。
• SRM
  （待补充）
  样本外误差估计有：
• k折验证
  通常用CV统计误差，其实就是求个误差平均值。
  K越小，Var越小；K越大，Bias越小。故通常需要多测试找个合适的K。
• 留一法（其实就是k折验证特殊）
• 广义交叉验证
  GCV提供了一种计算比较简单的近似方法：

\[GCV =\frac{1}{N}\sum^N_{i=1}[\frac{y_i-\hat f(x_i)}{1-\lambda}]^2 \]

其中\(\lambda = \frac{tr(S)}{N}\)，\(S\)是线性拟合的投影矩阵。

• Bootstrap
  我们可以通过足够次数的均匀抽样（不均匀的还有吉布斯采样等），得到每次采样样本拟合出来的err，也即得到err的分布。
  传统抽样与自助法的差别在于：传统抽样从真实的总体中进行随机抽样得到数据集直接进行统计量的估计；自助法抽样则是从训练集中抽出bootstrap数据集，得到的是统计量的bootstrap估计。
  预测误差估计如下：

\[\hat Err_{boot} = \frac{1}{B}\frac{1}{N}\sum^B_{b=1}\sum^N_{i=1} L(y_i,\hat f^{*b}(x_i)) \]

然而，假设每一个bootstrap集中含有原始三分之二的数据，那么这三分之二的数据对于误差的估计不起任何作用——在这些样本点上误差为0，于是倘若我们误差的真实值为 0.5，
\(\hat {Err}_{boot}\)的期望只有\(0.5×0.368=0.184\)。这是非常糟糕的。
利用交叉验证，我们可对其进行进一步地改进。对于每个观测，我们仅仅去计算利用不含该观测的bootstrap样本拟合出的模型对其的预测。从而，预测误差的去一自助法估计可以写为:

\[\hat Err^{(1)} =\frac{1}{N}\sum^N_{i=1}\frac{1}{|C^{-i}|}\sum_{b \in C^{-i}}L(y_i,\hat f^{*b}(x_i)) \]

这里\(C^{-i}\)表示那些不含第 i个样本的bootstrap集，个数为 \(|C^{-i}|\)。在计算\(Err^{(−1)}\)时，我们必须选择充分大的 B来保证所有的\(|C^{-i}|\)都大于零，或者我们可以直接删去等于零的项。解决了过拟合的问题，可是它还面临着“训练集大小偏差”。因为每一个自助法样本中不同观测的平均个数为2/3N ,所以它的偏差大致与两折交叉验证相同。
可利用两个err进一步改进，改进的err表达式如下：

\[\hat {err}^{(.632)}=0.368 \bar{err}+0.632 \hat {err}^{(1)} \]

这里0.368 是由1/e来的，1-1/e是样本大小为N的N 次抽样中某个元素至少一次被抽中的概率。从而\(err^{(.632)} = \bar {err}+(1-e^{-1})(\hat {err}-\bar {err})\)（待补充）

总结

误差分析与交叉验证/bootstrap

当解析误差估计值已知时，为什么还要考虑交叉验证和 bootstrap？
AIC, BIC, MDL, SRM 都需要知道参数个数，这在很多情况下很难知道。AIC, BIC 和 SRMVC 有优势，因为只需要知道训练误差。
Bootstrap 和交叉验证给出了与上述类似的结果，但也适用于更复杂的情况，给出的err标准差能帮助我们判断模型的稳定性。
如果 VC 维已知, 那么 SRM 是进行模型选择的一个很好的方法 −− 计算量比CV 和 bootstrap 小得多, 但是非常保守。像 CV， Bootstrap 这样的方法可以提供更严格的错误边界, 但是方差可能更大。
另外，渐近 AIC 和留一法 CV 是等价的，渐近 BIC 和认真选择的 k-折 CV 是等价的。