普通生成函数

普通生成函数

定义

对于一个序列 \(a_0, a_1, a_2, a_3, ..., a_n\)
用一个函数表示它 \(G(x) = a_0 + a_1 \times x + a_2 \times x ^ 2 + ... + a_n \times x ^ n\)
称 \(G(x)\) 是序列的普通生成函数

---

普通生成函数用来解决多重集组合问题

问题

有 \(n\) 种物品，每种物品有 \(a_i\) 个，问取 \(m\) 个的组合数

构造普通生成函数 ：

对于第 \(i\) 种物品，其生成函数为 \(\qquad G_i(x) = 1 + x + x ^ 2 + ... + x ^ {a_i}\)
求\(\qquad\prod_{i=1}^{n}G_i\)
得到了\(\qquad\sum_{j=0}^{m}b_jx^j \qquad (b_j为系数)\)
系数表示的是组合数，指数是选择的个数

如果问题为

有 \(n\) 种物品，每种物品有 \(a_i\) 个，每种物品至少取 \(c_i\) 个，问取 \(m\) 个的组合数

发现构成的生成函数为 \(\qquad G_i(x) = x ^ {c_i} + ... + x ^ {a_i}\)
同理，也可以得到答案

点击查看代码

#include <bits/stdc++.h>

using namespace std;

int n, m;

void solve() {
    vector<int> cnt(m + 1);
    cnt[0] = 1;
    for (int i = 0; i < n; i ++) {
        int a, b;
        cin >> a >> b;
        auto old = cnt;
        for (int j = 0; j <= m; j ++) {
            cnt[j] = 0;
        }

        for (int j = a; j <= b; j ++) {
            for (int k = 0; k + j <= m; k ++) {
                cnt[k + j] += old[k];
            }
        }
    }

    cout << cnt[m] << endl;
}

int main()
{
    ios::sync_with_stdio(false);
    cin.tie(nullptr);

    while (cin >> n >> m) {
        solve();
    }

    return 0;
}

如果问题为

有一定数量的 \(1\)、\(2\)、\(5\) 三种面值的硬币，求组合可以达到的金额

可以用指数来表示可以选择的个数，然后将生成函数相乘，所有系数非 \(0\) 的是可以选到的值
形如

\(\qquad G_1(x) = 1 + x + x ^ 2 + ... + x ^ {a}\)
\(\qquad G_2(x) = 1 + x ^ 2+ x ^ 4 + ... + x ^ {b \times 2}\)
\(\qquad G_5(x) = 1 + x ^ 5 + x^{10} + ... + x ^ {c \times 5}\)

求得 \(G_1 \times G_2 \times G_5\)
如果系数非 \(0\) 则代表可以取到 (预处理时\(x^0\)的系数为\(1\))

---

小凯爱数学

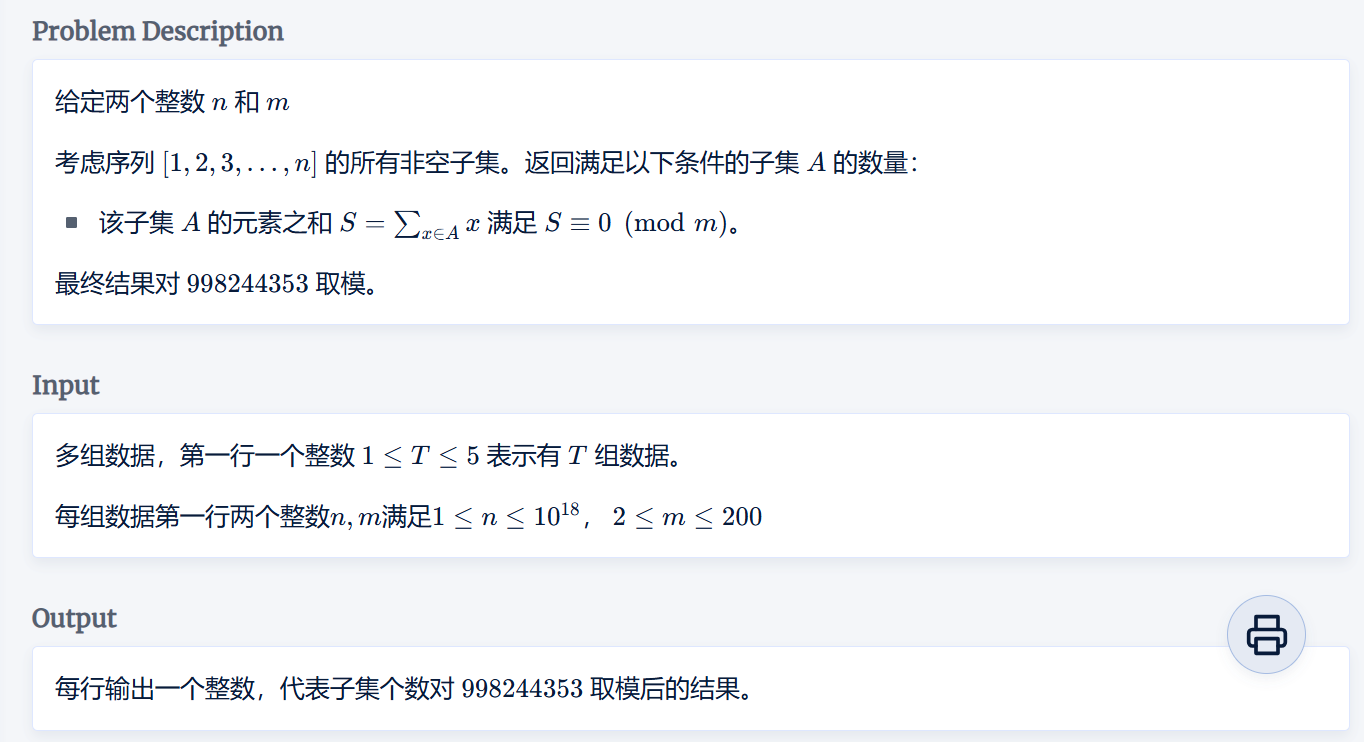
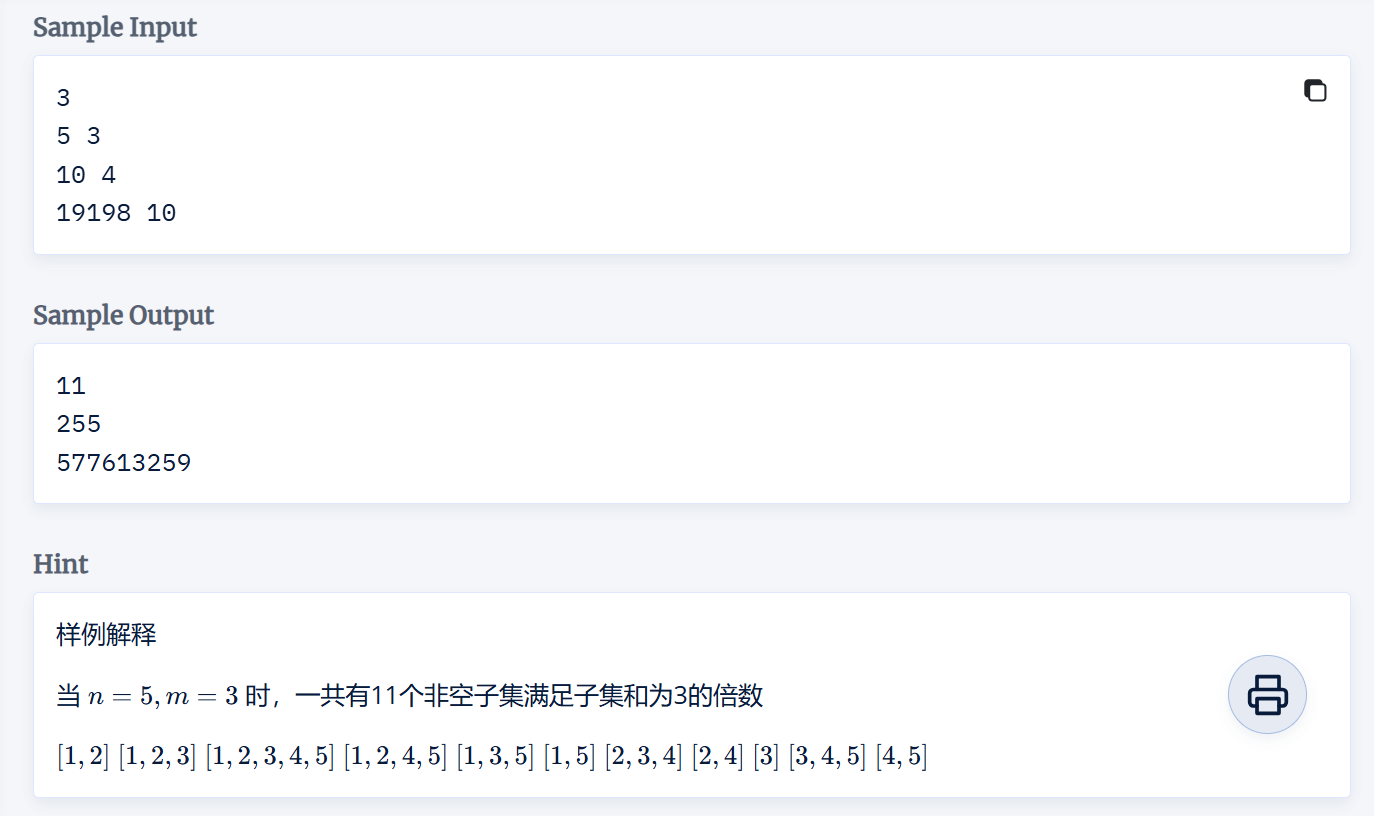
想求和为 \(S≡0(modm)\) 的组合数
\(m\) 相对较小，先求得余数为 \(0 \sim {m-1}\) 的数的个数
如果一个一个看的话，类似于 \(01\)背包问题，如果余数为 \(r\)
则生成函数为 \((1 + x^r)\)
最后得到的生成函数是 \(\prod_{i=0}^{m - 1}(1 + x^i)^{cnt_i}\)
这道题可以看作上方第三道例题的一种情况，因为 \(n\) 非常大，做一些优化来保证空间和时间
可以用类似快速幂的技巧，求得 \((1 + x^i)^{cnt_i}\) 的值
最终得到答案

代码

#include <bits/stdc++.h>

using namespace std;

typedef long long ll;
const ll mod = 998244353;

void times_g(vector<ll> &a, vector<ll> &b, int m) {
    vector<ll> res(m, 0);
    for (int i = 0; i < m; i ++) {
        if (a[i] == 0) continue;
        for (int j = 0; j < m; j ++) {
            if (b[j] == 0) continue;
            res[(i + j) % m] =(res[(i + j) % m] + a[i] * b[j]) % mod;
        }
    }
    a = res;
}

void qmi_g(vector<ll> &q, vector<ll> &p, ll b, int m) {
    vector<ll> res(m, 0);
    res[0] = 1;
    auto a = p;
    while (b) {
        if (b & 1) times_g(res, a, m);
        times_g(a, a, m);
        b >>= 1;
    }
    times_g(q, res, m);
}

void solve() {
    ll n, m;
    cin >> n >> m;

    vector<ll> cnt(m);
    for (int i = 0; i < m; i ++) {
        cnt[i] = n / m;
        if (i && n % m >= i) cnt[i] ++;
    }
    
    vector<ll> res(m, 0), a(m, 0);
    res[0] = a[0] = 1;
    for (int i = 0; i < m; i ++) {
        if (~(i - 1)) a[i - 1] --;
        a[i] ++; 
        qmi_g(res, a, cnt[i], m);
    }

    cout << (res[0] - 1 + mod) % mod << endl;
}

int main()
{
    ios::sync_with_stdio(false);
    cin.tie(nullptr);

    int t;
    cin >> t;

    while (t --) {
        solve();
    }

    return 0;
}